Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 85.92kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 129.5kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 107.65kb.
- Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию, 334.33kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 187.41kb.
- Рабочая программа учебной дисциплины ф тпу 21/01 Федеральное агентство по образованию, 307.9kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 217.64kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 236.22kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 266.17kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 216.78kb.
| Рабочая программа учебной дисциплины |  | Ф ТПУ 7.1 – 21/01 |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
----------------------------------------------------------------------------------------------------
УТВЕРЖДАЮ:
Декан АВТФ
__________С.А. Гайворонский
« » ________________ 2009 г.
ТЕОРИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Рабочая программа для специальности 080116 «Математические методы в экономике»
Факультет автоматики и вычислительной техники
Обеспечивающая кафедра прикладной математики
Курс четвертый
Семестр восьмой
Учебный план набора 2004 года с изменениями 2005 года
Распределение учебного времени
| Лекции Лабораторные занятия Практические занятия | 32 0 16 | часов (ауд.) часов (ауд.) часов (ауд.) |
| Всего аудиторных занятий | 48 | часов (ауд.) |
| | | |
| Самостоятельная (внеаудиторная) работа | 80 | часов |
| | | |
| Общая трудоемкость | 128 | часов |
| | | |
| Экзамен в 8 семестре | | |
| | | |
2009 г.
ПРЕДИСЛОВИЕ
1. Рабочая программа составлена на основе ГОС специальности 080116 «Математические методы в экономике», утвержденного приказом Минобразования РФ от 14.04.00г. №346эк/сп и стандарта СТП ТПУ 2.4.01-02 «Система образовательных стандартов. Рабочая программа учебной дисциплины. Общие требования к содержанию и оформлению».
рассмотрена и одобрена на заседании кафедры Прикладной математики (ПМ) «_____»__________2009 г., протокол № _____
- Разработчики:
Профессор кафедры прикладной математики ___________ В.А.Кочегуров
Доцент кафедры прикладной математик_______________Ю.В.Бабушкин
3. Зав. обеспечивающей кафедрой ПМ ____________ В.П.Григорьев
4. Рабочая программа СОГЛАСОВАНА с выпускающей кафедрой специальности; СООТВЕТСТВУЕТ действующему плану.
Зав. выпускающей кафедры ____________В.П.Григорьев
Ключевые слова: система, управление, оптимальное управление, вариационные методы, принцип максимума, динамическое программирование.
Аннотация
Рабочая программа по дисциплине "Теория оптимального управления" разработана для студентов, обучающихся по специальности 080116 - «Математические методы в экономике» очной формы обучения, содержит цели и задачи курса, его место в учебном процессе, теоретические и практические разделы дисциплины, программу самостоятельной познавательной деятельности, текущий и итоговой контроль, а также учебно-методическое обеспечение дисциплины.
В программе даются основные понятия, связанные с теорией оптимального управления.
Разработчики: Кочегуров В.А., кафедра ПМ, АВТФ, e-mail: am@am.tpu.ru
Бабушкин Ю.В., кафедра ПМ, АВТФ, e-mail: am@am.tpu.ru
- Цели и задачи
1.1. Цель преподавания дисциплины
В экономике для описания динамических процессов широко используются математические методы, разработанные в общей теории систем. Целью преподавания дисциплины является изложение математического аппарата, используемого в теории оптимального управления, постановка задач оптимального управления и изучение способов их решения. Приобретение навыков применения методов на конкретных примерах при выполнении практических заданий.
2. Содержание теоретического раздела дисциплины (лекции, 32 часа)
Основные определения. Системы управления. Структурное представление. Классификация по цели и способу управления, по виду математической зависимости, форме представления входных и выходных переменных.
Задачи проектирования систем управления: анализ и синтез. Анализ непрерывных, линейных, стационарных систем управления. Уравнения состояния и их решение. Переходная матрица и ее нахождение. Одномерные системы управления и их переходные характеристики.
Управляемость, наблюдаемость, чувствительность.
Устойчивость управления. Исследование устойчивости. Первый метод Ляпунова, второй метод Ляпунова.
Анализ дискретных систем управления. Уравнения состояния. Решение линейных уравнений состояния, переходная матрица.
Синтез систем управления. Качество управления: динамические и статические характеристики.
Оптимальное управление. Критерии, задачи оптимального управления. Особенности задач оптимального управления и методов их решения. Задачи оптимального управления по быстродействию, по расходу энергии, топлива.
Вариационное исчисление и оптимальное управление. Задачи линейного оптимального управления. Необходимые и достаточные условия. Уравнение Эйлера-Лагранжа, условие Лежандра, трансверсальности, Вейерштрасса. Управление конечным состоянием. Задача Майера. Задача Больца оптимального управления с обобщенным показателем.
Принцип максимума Понтрягина. Оптимальные по быстродействию системы. Применение принципа максимума к некоторым задачам.
Динамическое программирование. Принцип оптимальности. Динамическое программирование для непрерывных систем. Уравнение Беллмана. Практические примеры из экономики.
Общность методов оптимального управления и их взаимосвязь. Связь динамического программирования и принципа максимума Понтрягина, связь метода динамического программирования с вариационным исчислением.
Качественное исследование оптимальных траекторий динамических систем, магистральная теория.
3. Содержание практического раздела дисциплины (16 часов)
Целью практического раздела является научить студентов применять теоретические сведения к решению практических задач. Раздел содержит проведение практических занятий по следующим темам
| 1. | Определение связи вход-выход линейных систем | 2 часа |
| 2. | Определение связи вход-выход многомерных систем, методы определения переходной матрицы состояния | 2 часа |
| 3. | Структурные преобразования систем. Декомпозиция систем | 2 часа |
| 4. | Определение управляемости, наблюдаемости и устойчивости систем | 2 часа |
| 5. | Решение уравнения состояния систем, получение переходной матрицы | 2 часа |
| 6 7 8. | Определение оптимального управления вариационным методом Определение оптимального управления с помощью принципа максимума Понтрягина Определение оптимального управления методом динамического программирования | 2 часа 2 часа 2 часа |
5. Программа самостоятельной познавательной деятельности (80 часов)
Самостоятельная познавательная деятельность студентов предусматривает работу с учебной литературой и конспектом лекций при подготовке к практическим занятиям, выполнению лабораторных работ. Студенты самостоятельно изучают некоторые специальные разделы высшей математики, касающиеся особенностей математического описания задач оптимального управления. Каждому студенту предоставляется возможность выполнения индивидуального задания, в котором предусматривается дополнительная самостоятельная проработка основных разделов дисциплины с учетом приложения в экономике.
5.1. Тематика индивидуальных заданий
- структурные преобразования систем управления;
- связь дифференциальных уравнений со структурными схемами;
- методы декомпозиции систем;
- анализ систем во временной области и операторной форме;
- определение связи вход-выход в многомерных системах, методы определения переходной матрицы состояния;
- анализ наблюдаемости и управляемости систем;
- определение устойчивости систем управления, анализ качества управления;
- определение оптимального управления вариационным методом;
- определение оптимального управления с помощью принципа максимума Понтрягина;
- определение оптимального управления методом динамического программирования;
- определение магистрали.
6. Текущий итоговый контроль результатов изучения дисциплины
Текущий и итоговый контроль предполагает выявление уровня знаний, умения и навыков, приобретаемых и усваиваемых каждым студентом при изучении отдельных тем, а также дисциплины в целом.
Контроль осуществляется на основе ежегодно составляемого рейтинг-листа, в котором в соответствии с учебным и календарным планами указаны все формы и сроки отчетности. Согласно положению о рейтинговой системе оценки знаний определено максимальное количество баллов по всей дисциплине, которое равномерно распределено по отдельным темам и формам контроля в течение семестра.
Важное значение в контролирующих материалах уделяется выполнению индивидуальных заданий, рассчитанных на обязательную систематическую работу по каждой теме в течение всего семестра.
6.1. Контрольные вопросы
- Общие понятия. Структурное представление систем управления.
- Преобразование структурных схем: декомпозиция, агрегирование.
- Классификация систем управления.
- Задачи проектирования систем управления.
- Проблемы качества управления, законы управления.
- Анализ непрерывных линейных стационарных систем управления. Уравнения состояния.
- Решение уравнений состояния. Переходная матрица. Вычисление переходной матрицы.
- Устойчивость управления. Первый и второй методы Ляпунова.
- Анализ дискретных систем управления. Взаимосвязь методов описания дискретных и непрерывных систем управления.
- Уравнения состояния дискретных систем управления, переходная матрица.
- Синтез систем управления, качество управления, динамические и статические характеристики управления.
- Оптимальное управление. Критерии и задачи оптимального управления.
- Задачи оптимального быстродействия по расходу энергии и топлива.
- Вариационное исчисление и оптимальное управление. Задача Лагранжа.
- Необходимые и достаточные условия оптимального управления.
- Оптимальное управление в задачах о конечном состоянии. Задачи Майера, Больца.
- Принцип максимума Понтрягина. Задача о максимальном быстродействии.
- Применение принципа максимума к решению экономических задач.
- Динамическое программирование. Принцип оптимальности.
- Динамическое программирование для непрерывных систем управления. Уравнение Беллмана.
- Дискретный анализ динамического программирования. Приложения к экономическим задачам.
- Общность методов оптимального управления и их взаимосвязь.
- Связь динамического программирования и принципа максимума Понтрягина.
- Связь динамического программирования с вариационным исчислением.
- Качественное исследование оптимальных траекторий динамических систем, магистральная теория.
6.2. Контрольные задания
1. Даны уравнения состояния системы
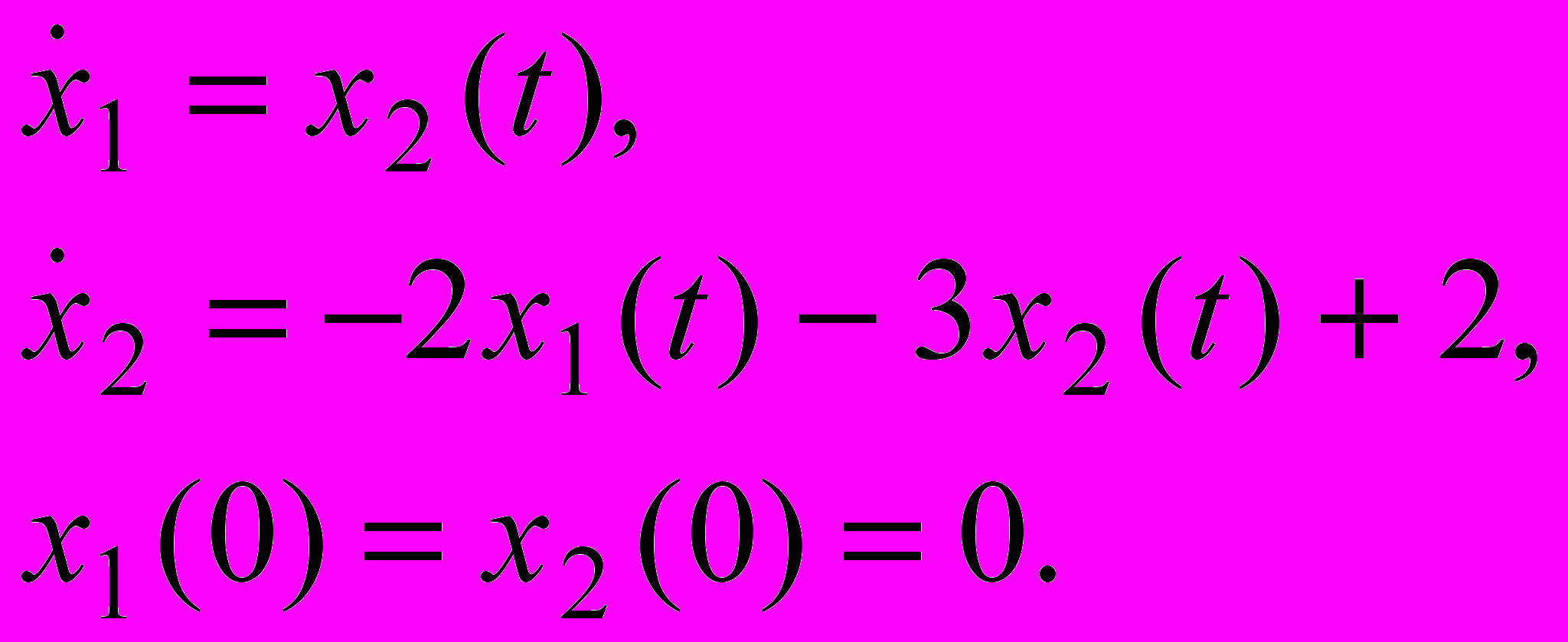
Найти решение уравнений состояния, записать выражение для переходной матрицы.
2. Заданы уравнения системы управлений
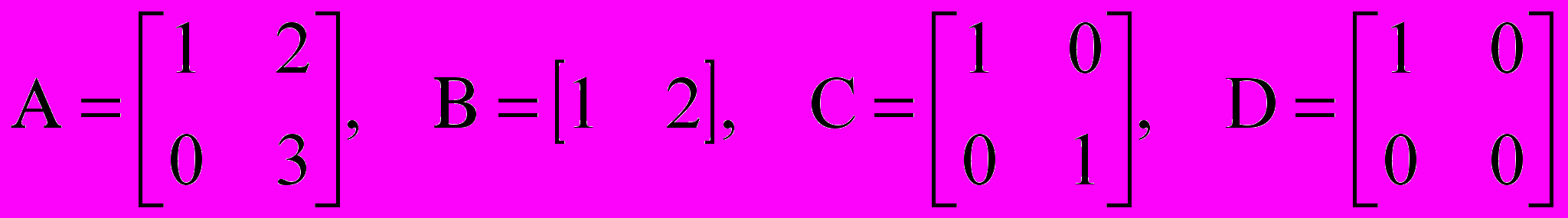.Нарисовать структурную схему системы управлении.
3. Задано уравнение системы управления
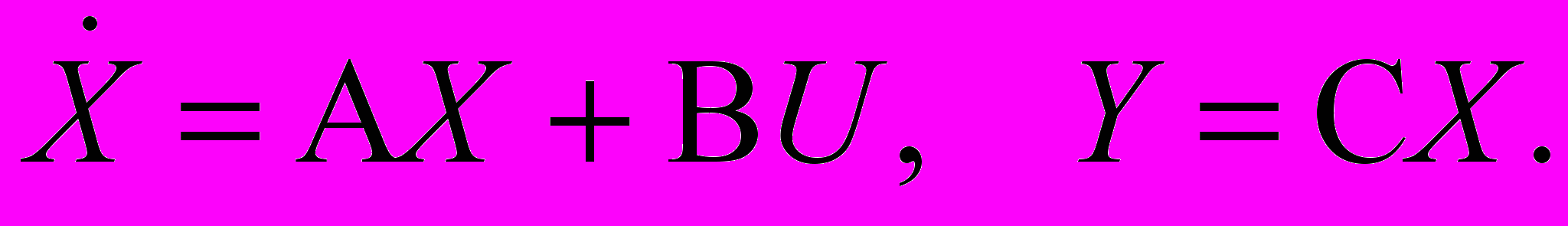
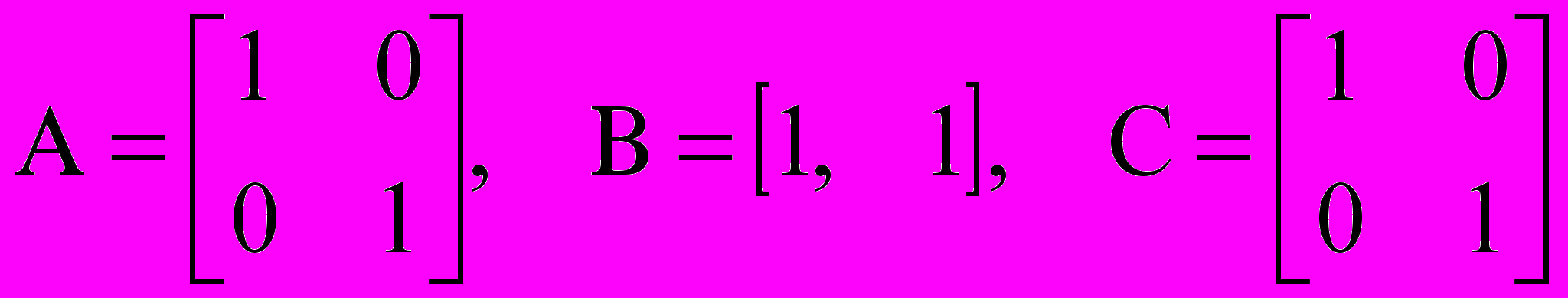.Определить управляемость и наблюдаемость системы.
4. Найти функцию, удовлетворяющую граничным условиям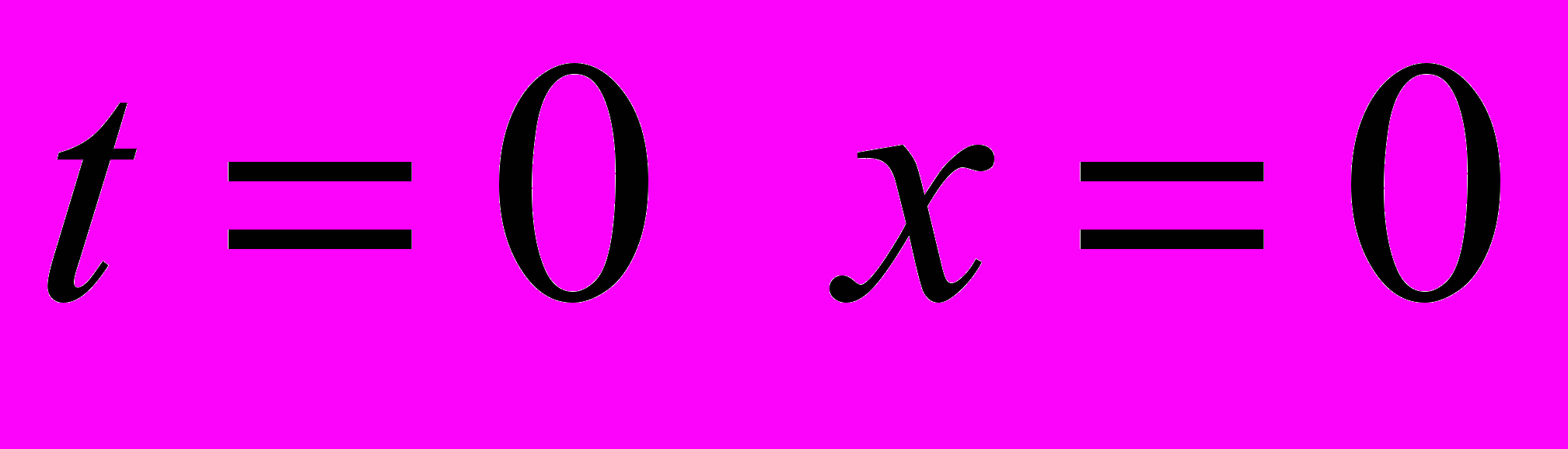: при
, при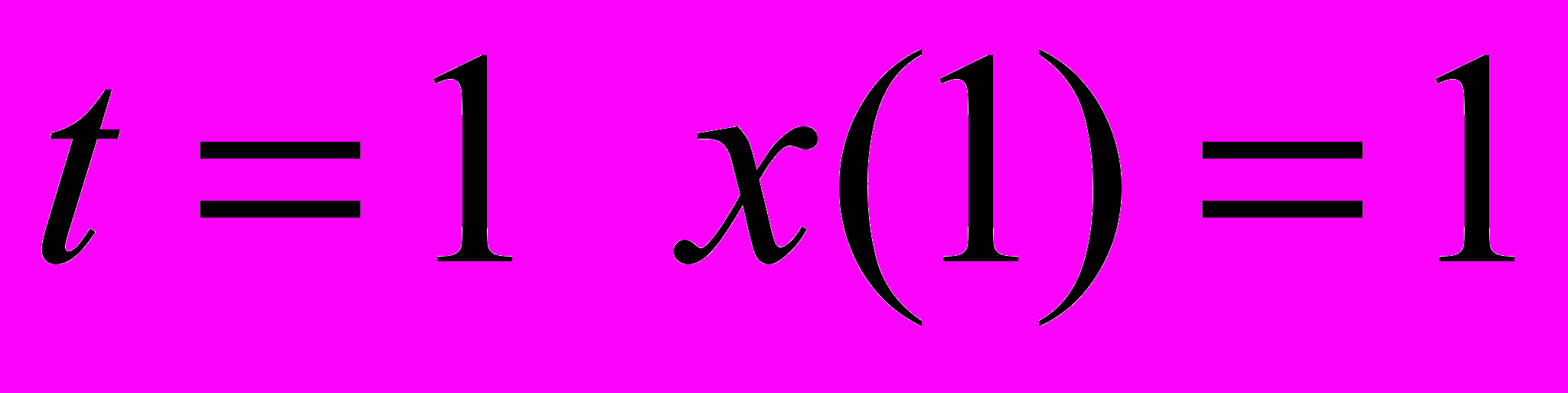 
и минимизирующую функционал 
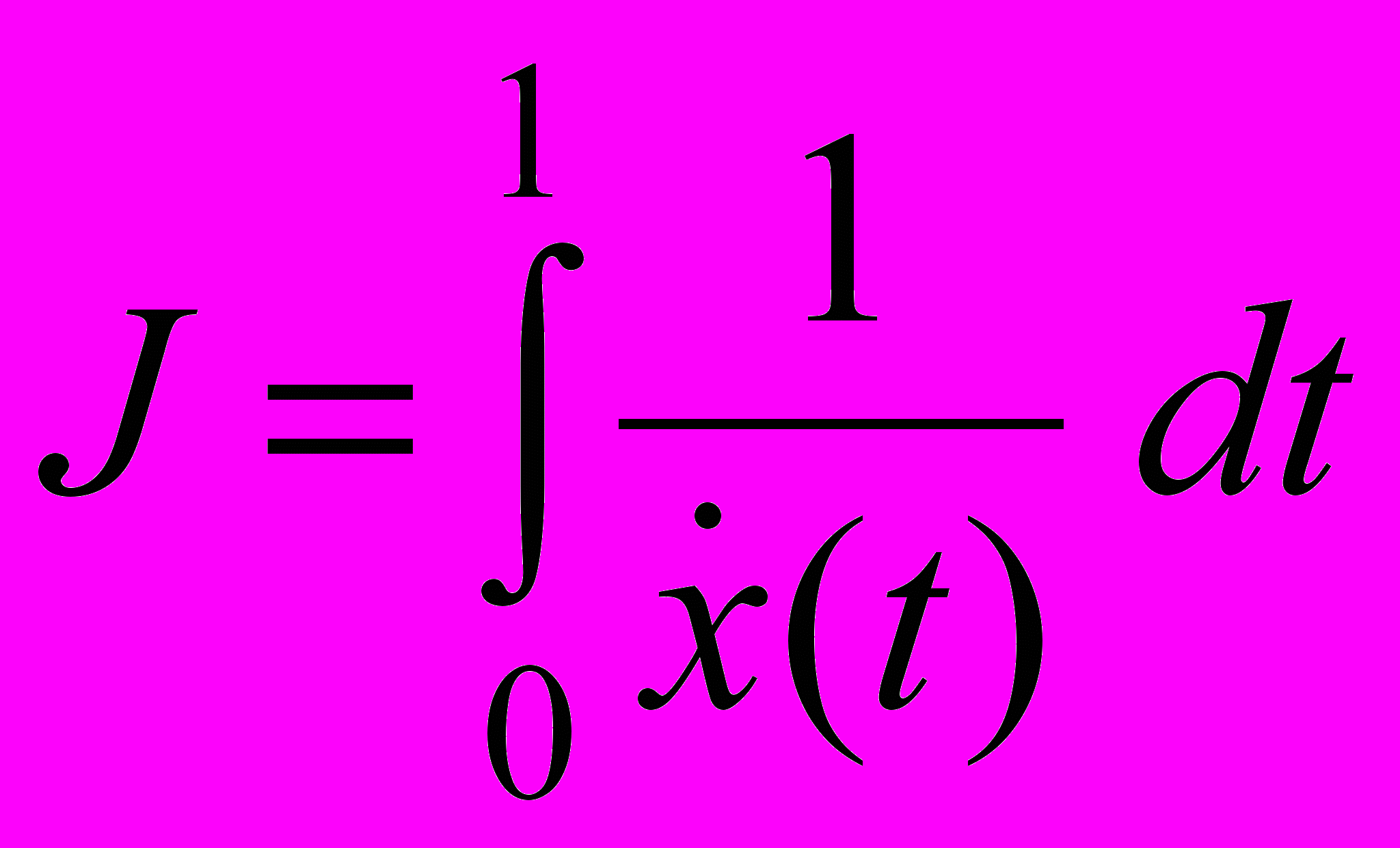.Ответ:
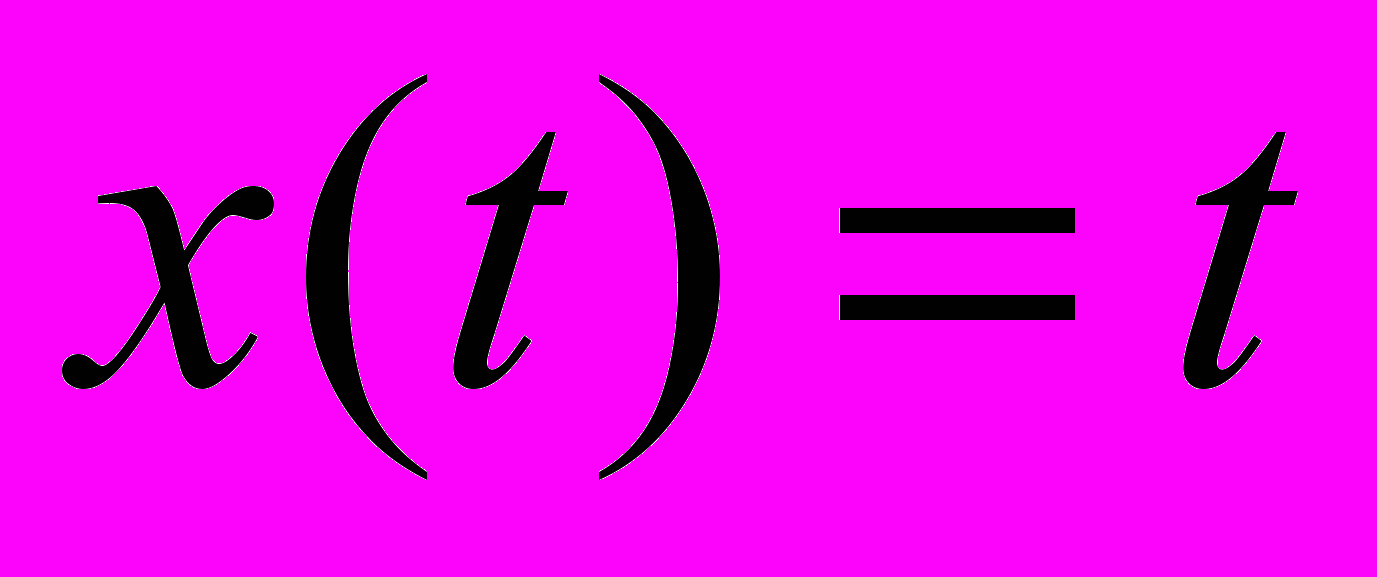.5. Определить линейное оптимальное управление для системы
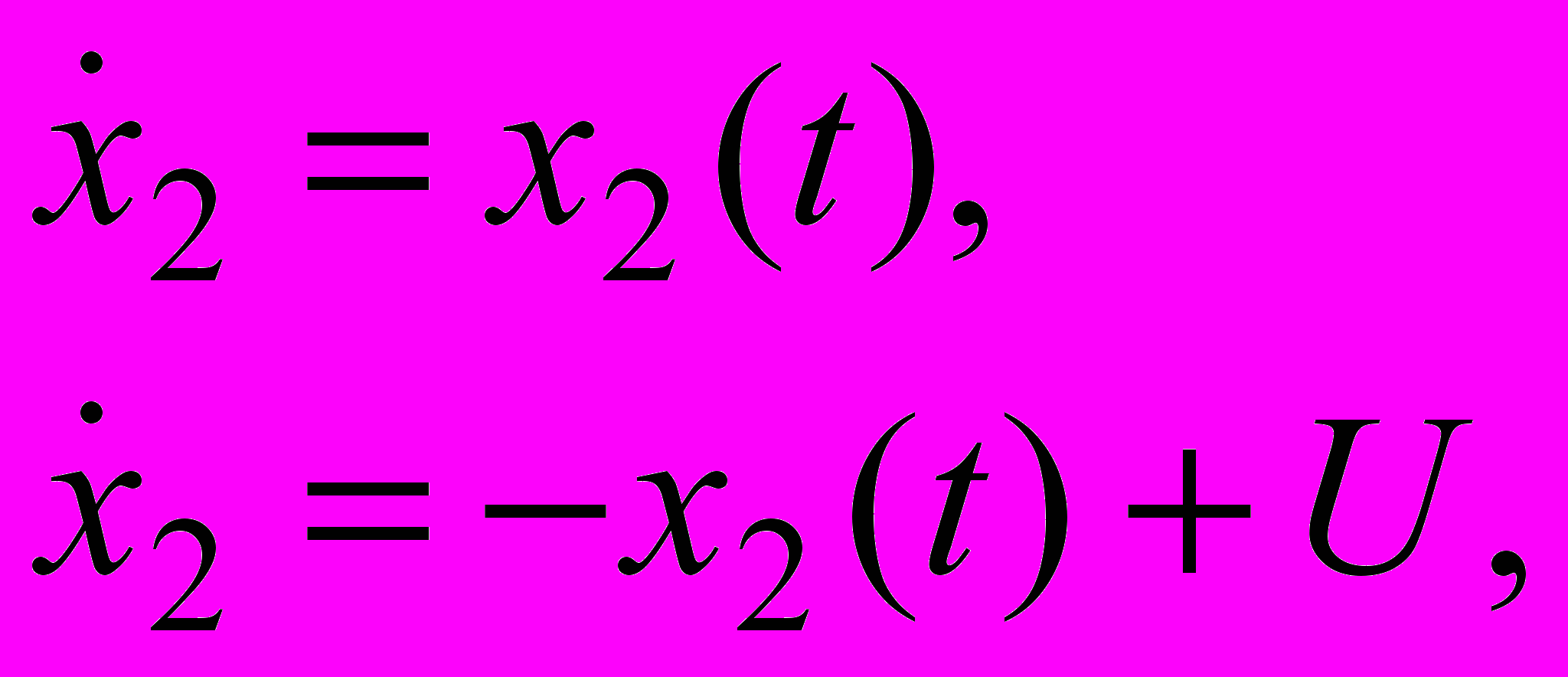
принимая во внимание показатель качества
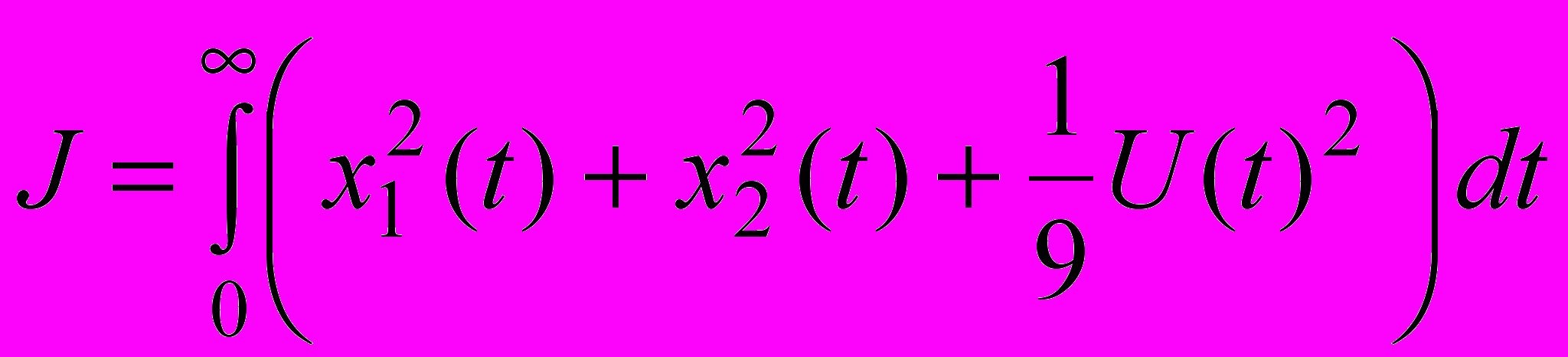
и граничные условия
, 
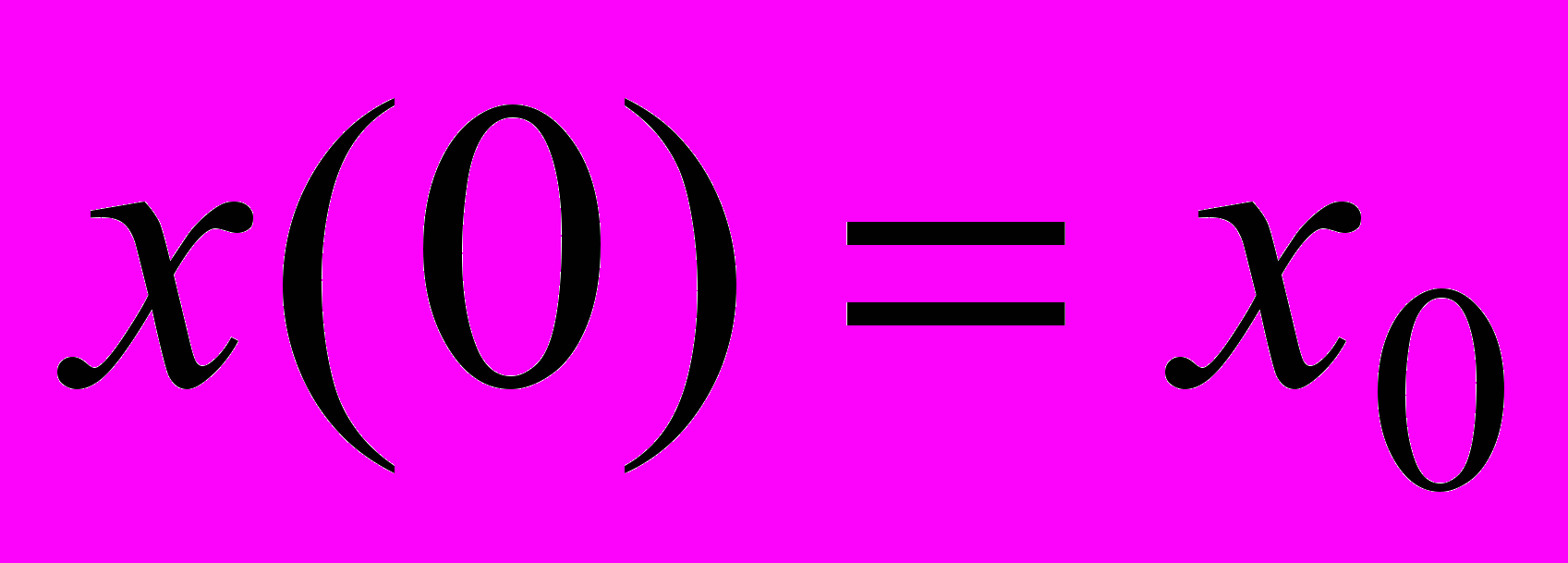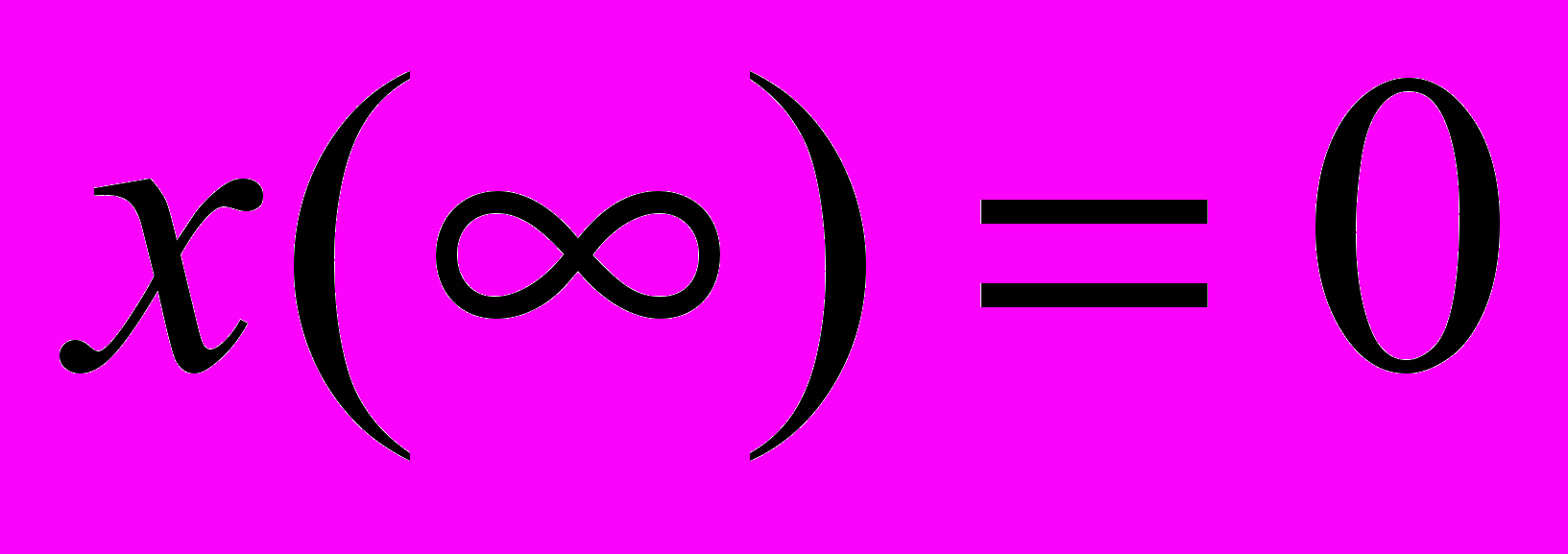.Ответ:
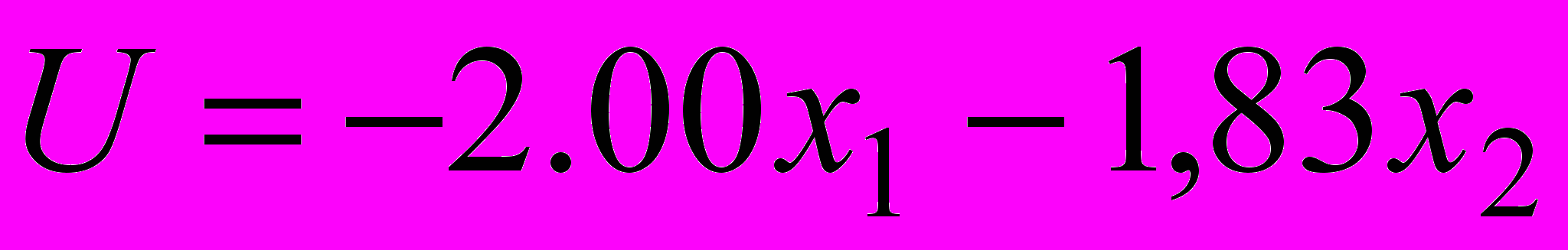.6. Учебно-методическое обеспечение дисциплины
- Основы теории оптимального управления. Под ред. Кротова В.Ф. – М.: Изд-во Высшая школа. 1990.
- Теория управления в примерах и задачах. Учебное пособие. . – М.: Изд-во Высшая школа. 200390.
- Сборник задач по теории автоматического регулирования и управления. - Под ред. В.А.Бессекерского. М.: Изд-во Наука, 1978.
- Гранберг А.Г. Динамические модели народного хозяйства, 1985.
Документ: Рабочая программа
Дата разработки: «01» сентября 2004г.