Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию

Вид материала

Рабочая программа

Содержание Рейтинг - лист Рейтинг за семестр 1000 баллов Дифференциальные уравнения 1-го порядка Дифференциальные уравнения высших порядков. Системы дифференциальных уравнений Коллоквиум «Дифференциальные уравнения и системы» Комплексные числа и функции Элементы теории вероятностей Итого за семестр 6. Учебные пособия кафедры ВММФ Образцы контролирующих материалов

Подобный материал:

• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 85.92kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 101.07kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 129.5kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 107.65kb.
• Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию, 334.33kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 187.41kb.
• Рабочая программа учебной дисциплины ф тпу 21/01 Федеральное агентство по образованию, 307.9kb.
• Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 217.64kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 236.22kb.
• Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 266.17kb.

Рейтинг - лист

по курсу «Высшая математика»

для студентов 2 курса ФТФ ТПУ

(специальности 251700, 250900)

семестр III


Лекции 44 часа

Практические занятия 44 часа

Самостоятельная работа 87 часов

Общая трудоемкость 175 часов

Рейтинг за семестр 1000 баллов

(допуск к экзамену 450 баллов)

	Тема	Отчетность	Срок (неделя)	Балл	Итого по теме
1	Дифференциальные уравнения 1-го порядка	Индивидуальное задание 13 Контрольная работа 14	5 5	60 90	150
2	Дифференциальные уравнения высших порядков. Системы дифференциальных уравнений	Индивидуальное задание 13 Контрольная работа 15	9 9	80 90	170
	Коллоквиум «Дифференциальные уравнения и системы»		10	180
5	Комплексные числа и функции	Индивидуальное задание 14 Контрольная работа 16	12	40 60	100
6	Элементы теории вероятностей	Индивидуальное задание 15 Контрольная работа 17	16	40 60	100
	Экзамен			300
	Итого за семестр				1000

6. Учебно – методическое обеспечение дисциплины

1. Линейная алгебра и аналитическая геометрия
   

Основная литература:

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М. Наука, 1976, 1980, 1984, 1987 гг. - 336 с. – 1273 экз.

2. Элементы линейной алгебры и аналитической геометрии./Апатенок Р.Ф. и др./ - М. Наука, 1987г. - 273 с. - 290 экз.

3. Головина Л.И. Линейная алгебра и некоторые её приложения. - М. Наука, 1975, 1979, 1985 гг. – 392 с. - 246 экз.

4. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. - М. Наука, 1987,1989 гг.- 496с.- 410 экз.

5. Клетеник Д.В. Сборник задач по аналитической геометрии. - М. Наука, 1975, 1980, 1986 гг. - 240 с. - 835 экз.

6. Проскуряков И.В. Сборник задач по линейной алгебре. - М. Наука, 1970, 1978, 1984 гг. - 446 с. -232 экз.

Дополнительная литература:

7. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М. Наука, 1979 г. - 511 с. - 119 экз.

8. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М. Наука, 1980, 1984, 1988 гг. - 190 с. - 159 экз.

9. Ильин В.А., Позняк Э.Г. Линейная алгебра. - М. Наука, 1974, 1978, 1984 гг. - 234 с. - 94 экз.

10. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. - М. Наука, 1971, 1981, 1988 гг. - 232 с. – 207 экз.

11.Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. - М. Наука, 1977. - 288 с. - 137 экз.

12. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. - М. Наука, 1968, 1970 гг. - 336 с. - 271 экз.

2. Математический анализ
   

Основная литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисление (в 2-х томах) - М. Наука, Математический анализ:1967, 1978, 1985, 1986 гг. – 1031 с. - 2710 экз.

2. Кудрявцев Л.Д. Курс математического анализа (в 3-х томах).- М. Наука, 1970, 1981, 1988 гг. – 1639 с. - 524 экз.

3. Никольский С.М. Курс математического анализа (в 2-х томах).- М. Наука, 1975, 1983, 1990 гг. - 822 с. - 360 экз.

4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М. Наука, 1980,1984,1988 гг. -432 с. - 268 экз.

1. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. - М. Наука, 1981,1985,1988,1989 гг. -448 с. - 432 экз.
   

6. Берман Г.Н. Сборник задач по курсу математического анализа. - М. Наука, 1972, 1975, 1977, 1985 гг. - 416 с. - 1422 экз.

7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М. Высшая школа, 1980, 1986 гг. - 718 с. - 2790 экз.

8. Задачи и упражнения по математическому анализу (Под ред. Демидовича Б.П.) - М. Наука, 1972, 1978, 1990 гг. - 479 с. - 436 экз.

1. Минорский В.П. Сборник задач по высшей математике. - М. Наука, 1969, 1978, 1987 гг. - 352 с. - 405 экз.
   

10. Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. - М.: Наука, 1965, 1968 гг. - 416 с. - 46 экз.
    
11. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. — М.: Наука, 1965, 1973 гг. -736 с. - 249 экз.
    
12. Пчелин Б.К. Специальные разделы высшей математики.- М.: Наука, 1973 г. -461 с.-100 экз.
    
13. Свешников А.Г., Тихонов А.Н. Теория функций комплексного переменного. - М.: Наука, 1970, 1974 гг. - 319 с. - 194 экз.
    
14. Волковыский Л.И., Лунц Г.Л.., Араманович И.Г. Сборник задач по теории функции комплексного переменного. -М. Наука, 1970, 1975 гг. - 319 с. - 82 экз.
    
15. Краснов М.Л., Киселев А.И. Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Задачи и упражнения. - М. Наука, 1975, 1981 гг. - 303 с. - 279 экз.
    
16. Вентцель Е.С. Теория вероятностей. — М. Физматгиз, 1962.
    
17. Гмурман В.Е. Теорию вероятностей и математическая статистика. — М. Высшая школа, 1999.
    
18. Гмурман В.Е. Сборник задач по теории вероятностей и математической статистике. — М. Высшая школа, 1999.
    

Дополнительная литература:

10. Фихтенгольц Г.М. Основы математического анализа (в 2-х томах).- М. Наука, 1960, 1968 гг. - 903 с. - 38 экз.
    
11. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (в 3-х томах) - М. Наука, 1962, 1970 гг. - 2063 с. - 78 экз.
    
12. Шнейдер В.Е. и др. Краткий курс высшей математики (в 2-х томах ). - М. Наука, 1978. - 384 с. – 280 экз.
    
13. Мантуров О.В., Матвеев Н.И. Курс высшей математики. - М. Наука,1980 г. - 480 с. - 299 экз.
    
14. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. - М. Наука , 1973 г. – 720 с. – 155 экз.
    
15. ЗапорожецГ.Н. Руководство к решению задач по математическому анализу. - М. Высшая школа, 1966 г. –460 с. -256 экз.
    
16. Кузнецов Л.А. Сборник задач по высшей математике. – М. Наука, 1983г. -175 с. - 112 экз.
    
17. Сборник задач по математике для  втузов (под ред. Ефимова А.В.) - М. Наука, 1981, 1986 гг. - 836 с. - 120 экз.
    
18. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. - М. Наука, 1979,1985 гг. -127 с. - 107 экз.
    
19. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. - М.: Наука, 1976, 1982 гг. - 488 с. -77 экз.
    
20. Шабат Б.В. Введение в комплексный анализ. - М.: Наука, 1969, 1976, 1985 гг. - 320 с. -45 экз.
    
21. Сборник задач по теории аналитических функций /под ред. Евграфова М.А. / - М. Наука, 1969, 1972 гг. - 387 с. - 105 экз.
    

6. Учебные пособия кафедры ВММФ

1. Терехина Л.И., Фикс И.И. Высшая математика, часть 1.Линейная алгебра, векторная алгебра, аналитическая геометрия. Учебное пособие. — Томск, ТПУ, 2008, - 224 с.
   
2. Терехина Л.И., Фикс И.И. Высшая математика, часть 2. Предел, непрерывность, производная, приложения производной, функции нескольких переменных. Учебное пособие. — Томск, Дельтаплан, 2009, - 192 с.
   
3. Терехина Л.И., Фикс И.И. Высшая математика, часть 3.. Неопределенный интеграл. Определенный интеграл. Кратные интегралы. Теория поля. Учебное пособие. — Томск, Дельтаплан, 2008, - 252 с.
   
4. Терехина Л.И., Фикс И.И. Высшая математика, часть 4. Дифференциальные уравнения. Ряды. Функции комплексного переменного. Операционный метод. Учебное пособие. — Томск, Дельтаплан, 2009, - 268 с.
   
5. Багров В.Г., Белов В.В., Задорожный В.Н., Трифонов А.Ю. Методы математической физики. - Томск: Изд-во НТЛ, 2002. - 672 с. (Гриф МО)
   
6. Задорожный В.Н., Зальмеж В.Ф., Трифонов А.Ю., Шаповалов А.В. Высшая математика для технических университетов. IV. Ряды.- Томск: Изд. ТПУ, 2006
   
7. Задорожный В.Н., Зальмеж В.Ф., Трифонов А.Ю., Шаповалов А.В. Высшая математика для технических университетов. V. Дифференциальные уравнения.- Томск: Изд. ТПУ, 2007
   
8. Терехина Л.И., Фикс И.И. Сборники индивидуальных заданий. Высшая математика для студентов 1-го и 2-го курса. Рег. № , 2003 г.,- 408 с.
   

Образцы контролирующих материалов

Экзаменационный билет № 1

Дисциплина:

Высшая математика

Факультет: ФТФ

Курс 1, семестр 1

1. Решить систему
   

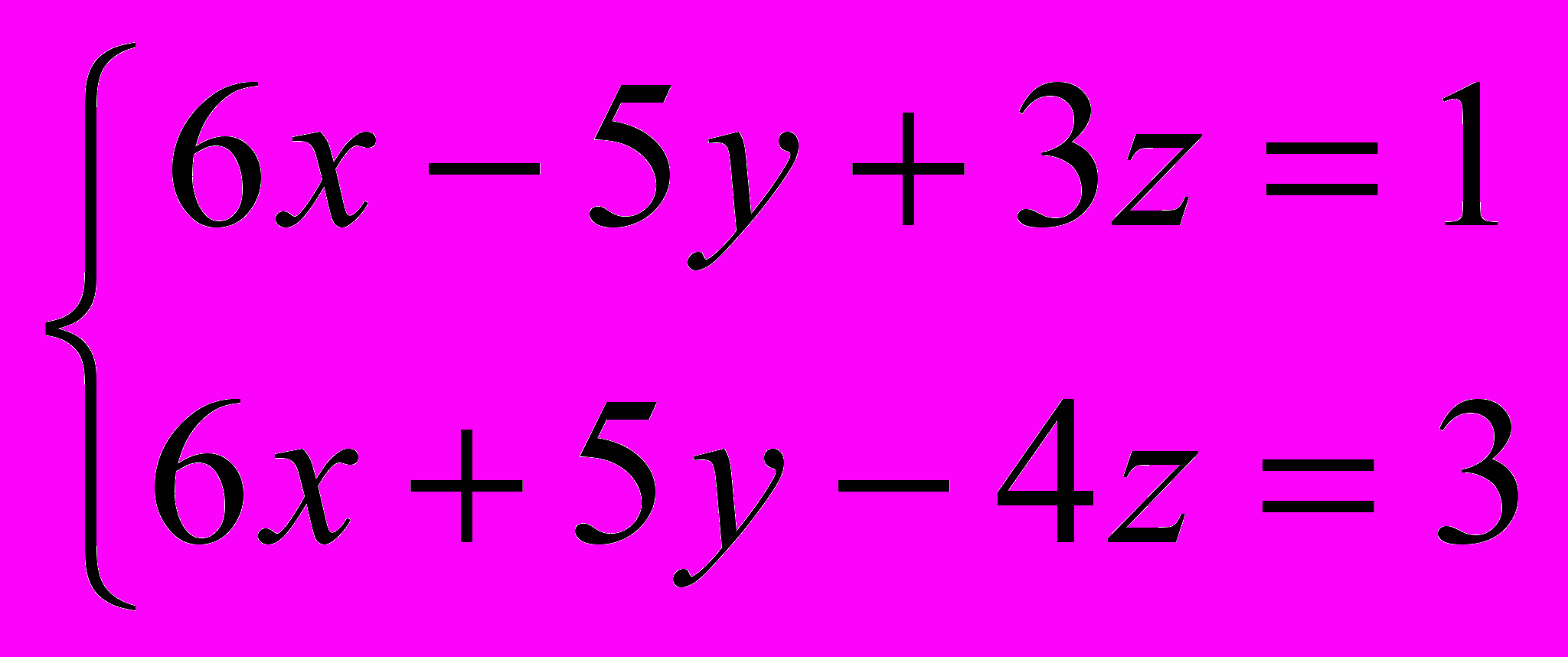
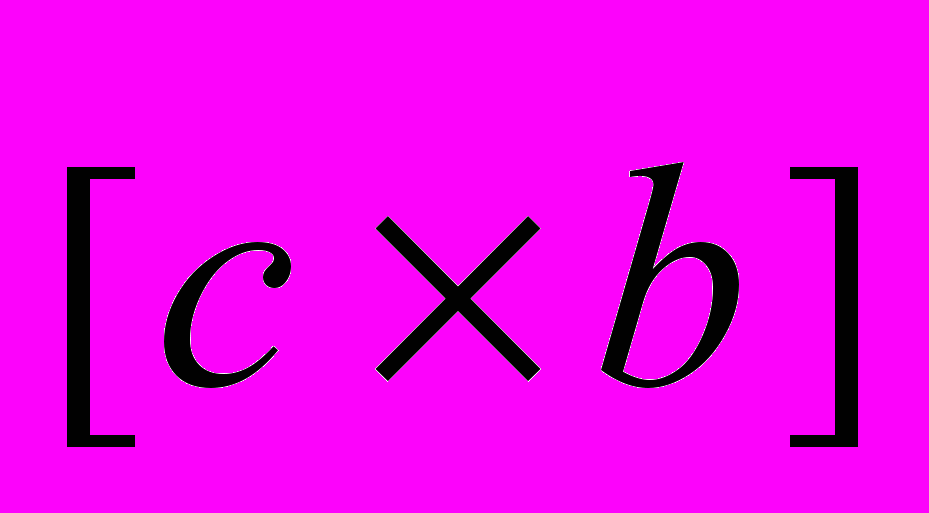
2. Найти модуль векторного произведения | 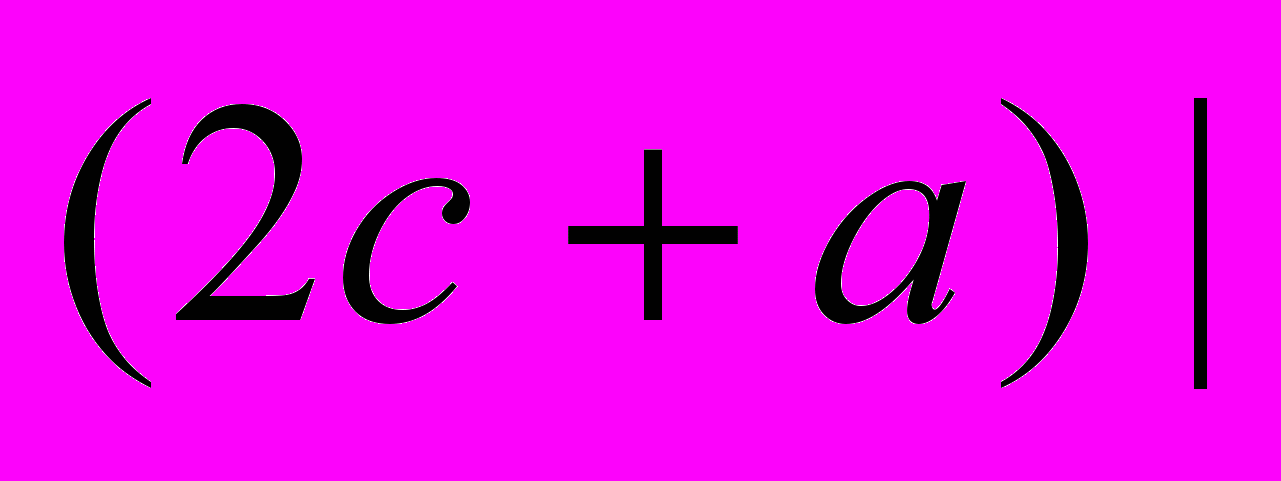, если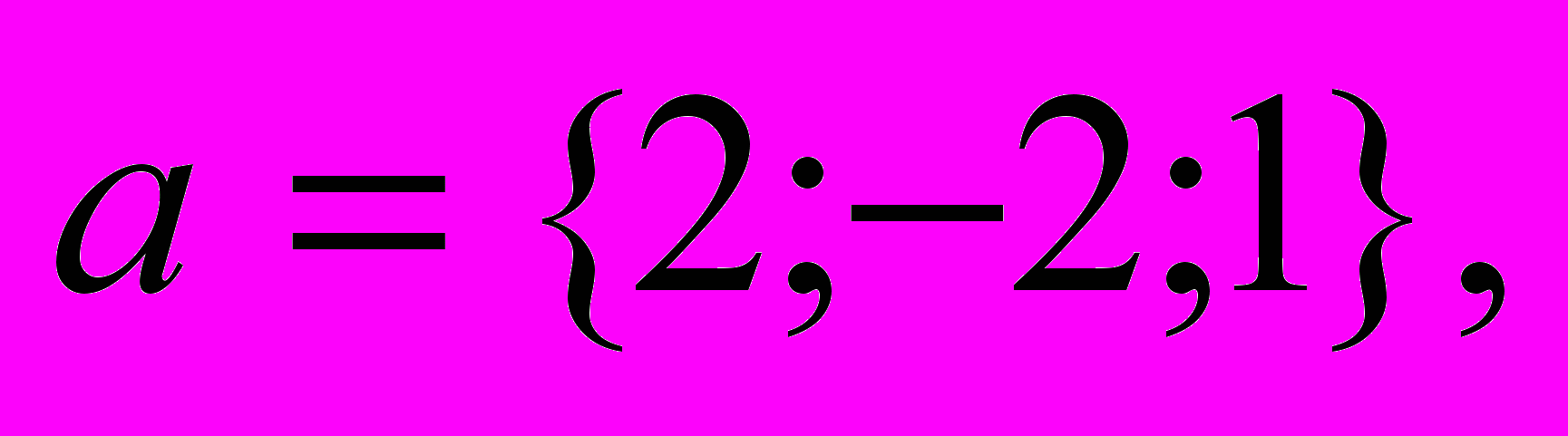 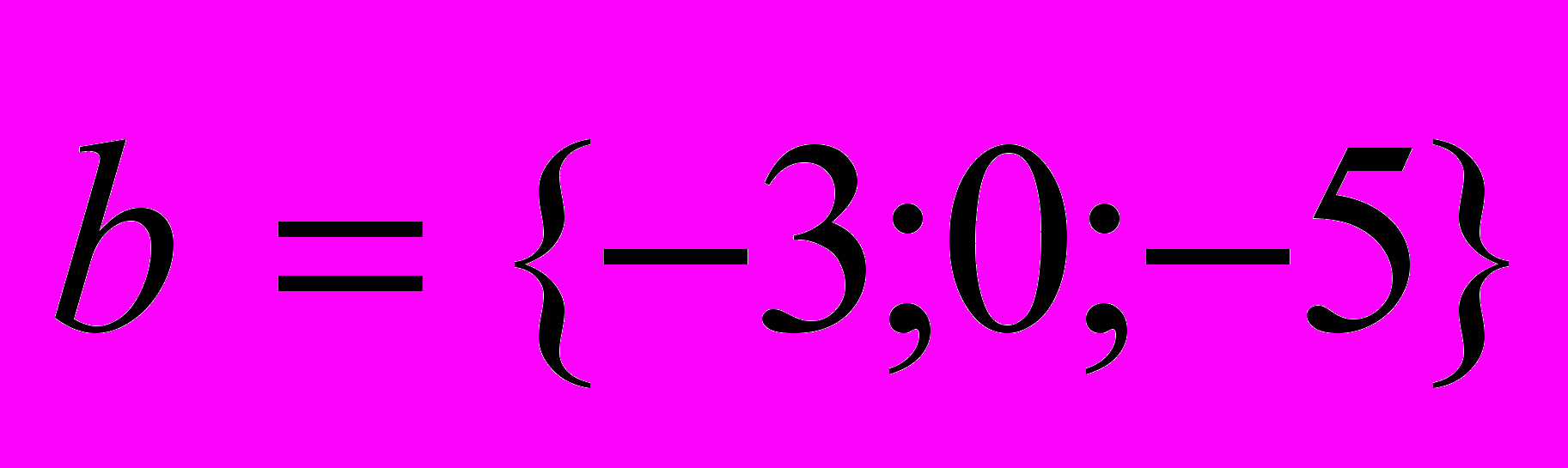и .
   
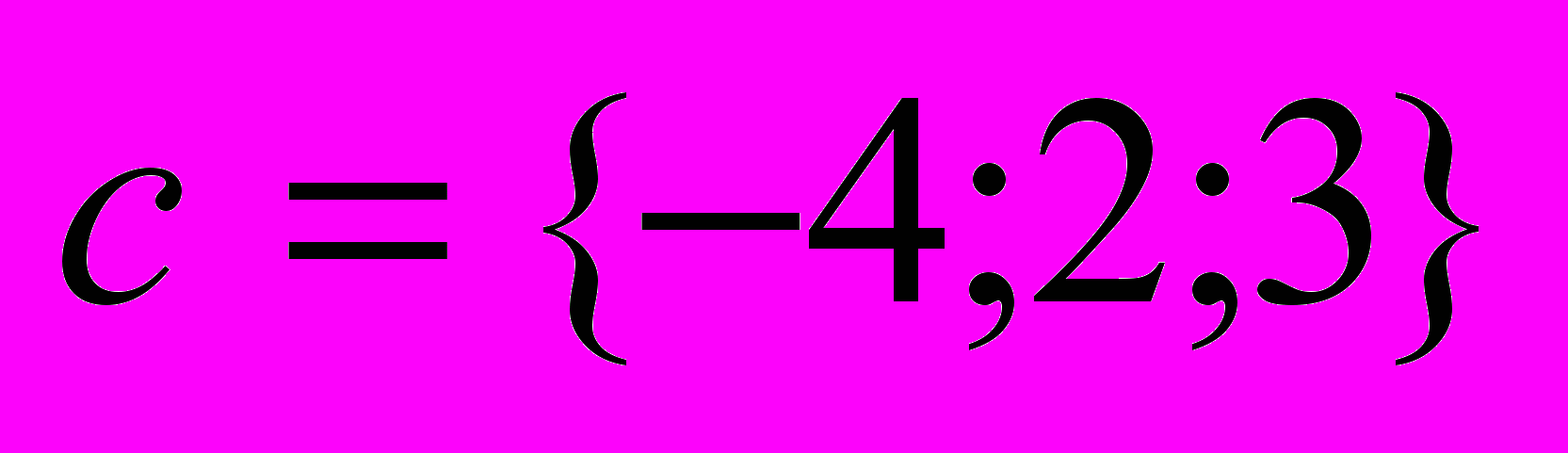3. Найти точку пересечения и угол между прямой 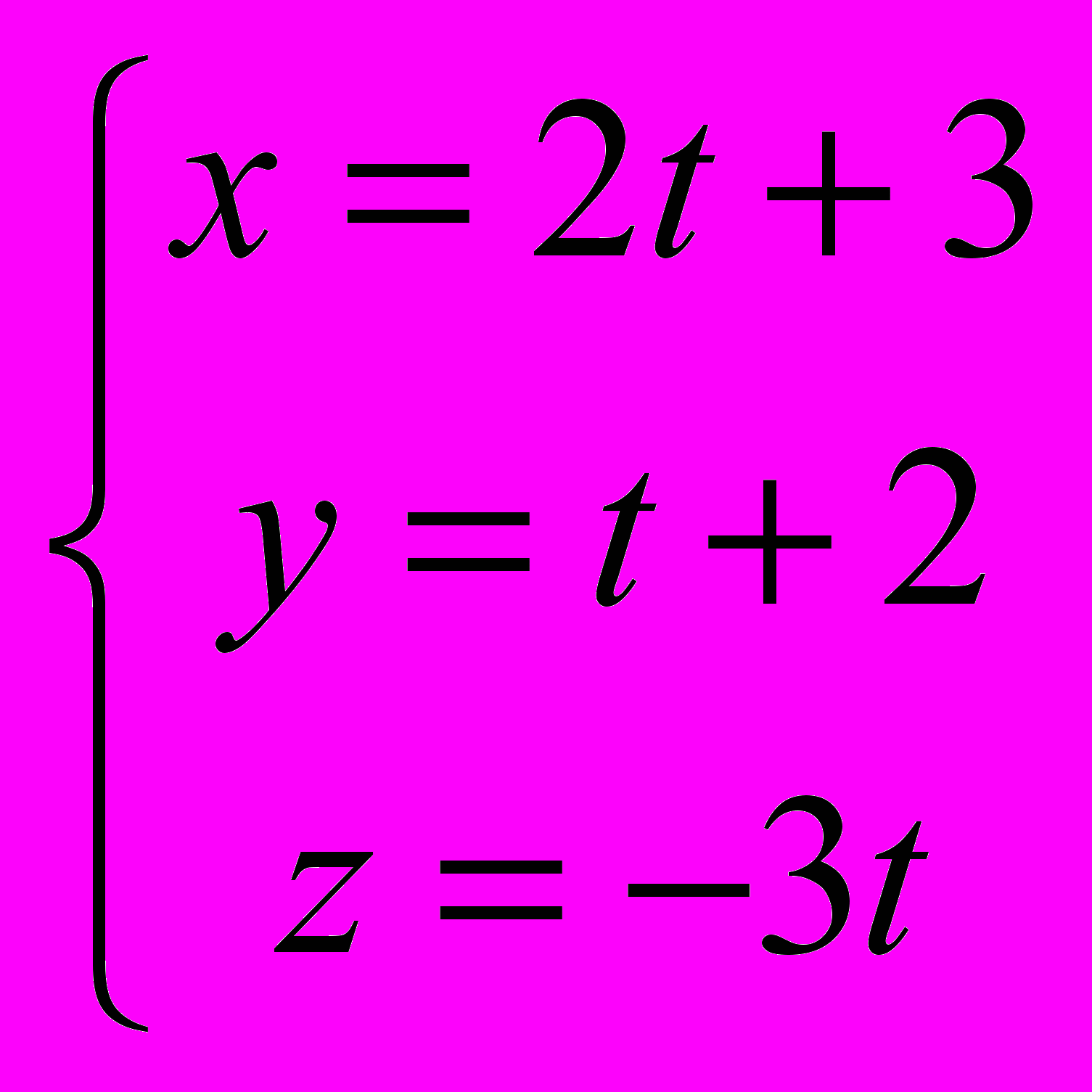и плоскостью .
   
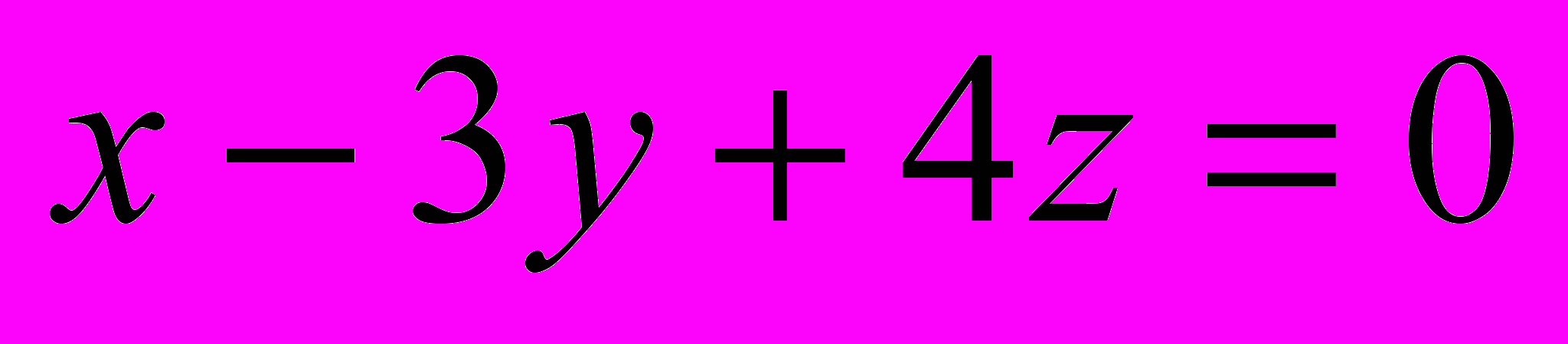4. Построить
   

а) кривую

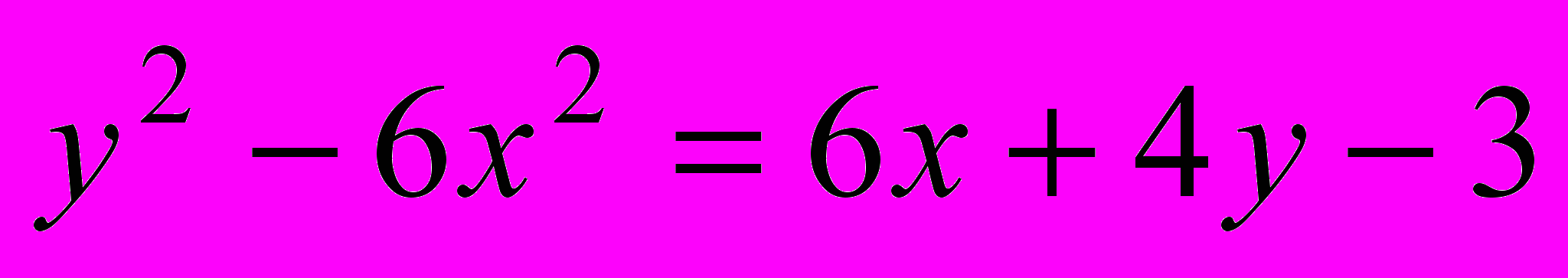
b) поверхность

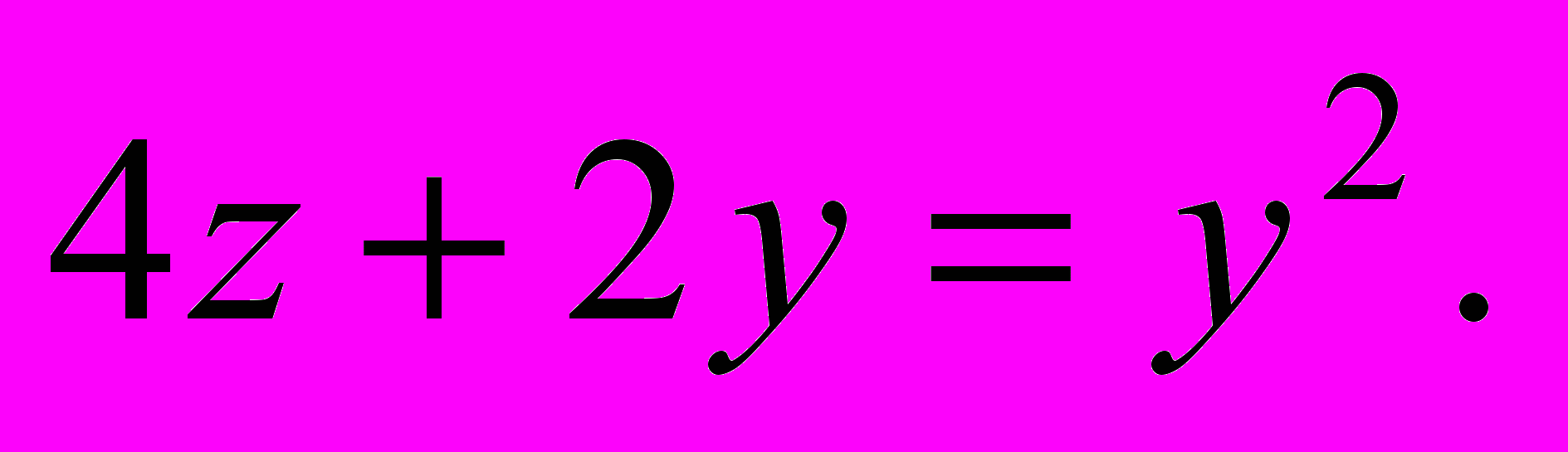
5. Вычислить пределы
   

a) 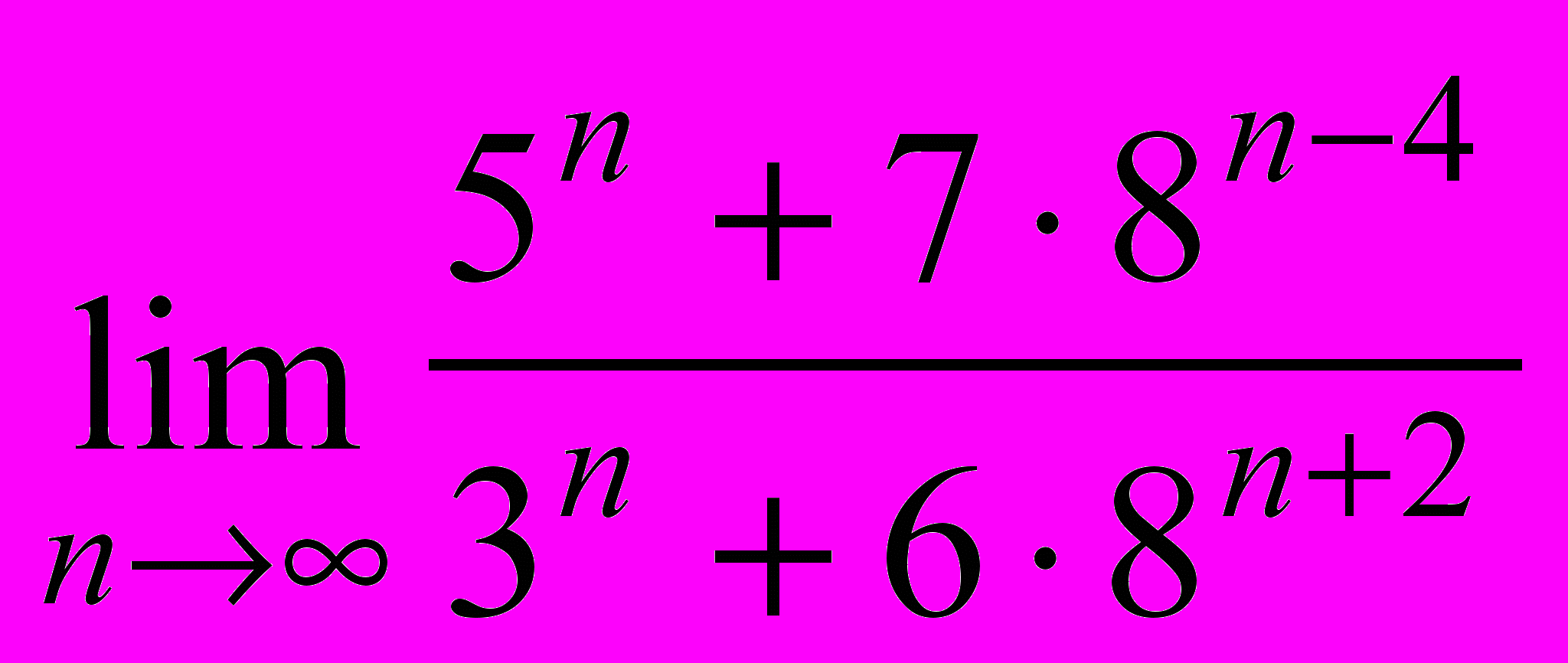b)

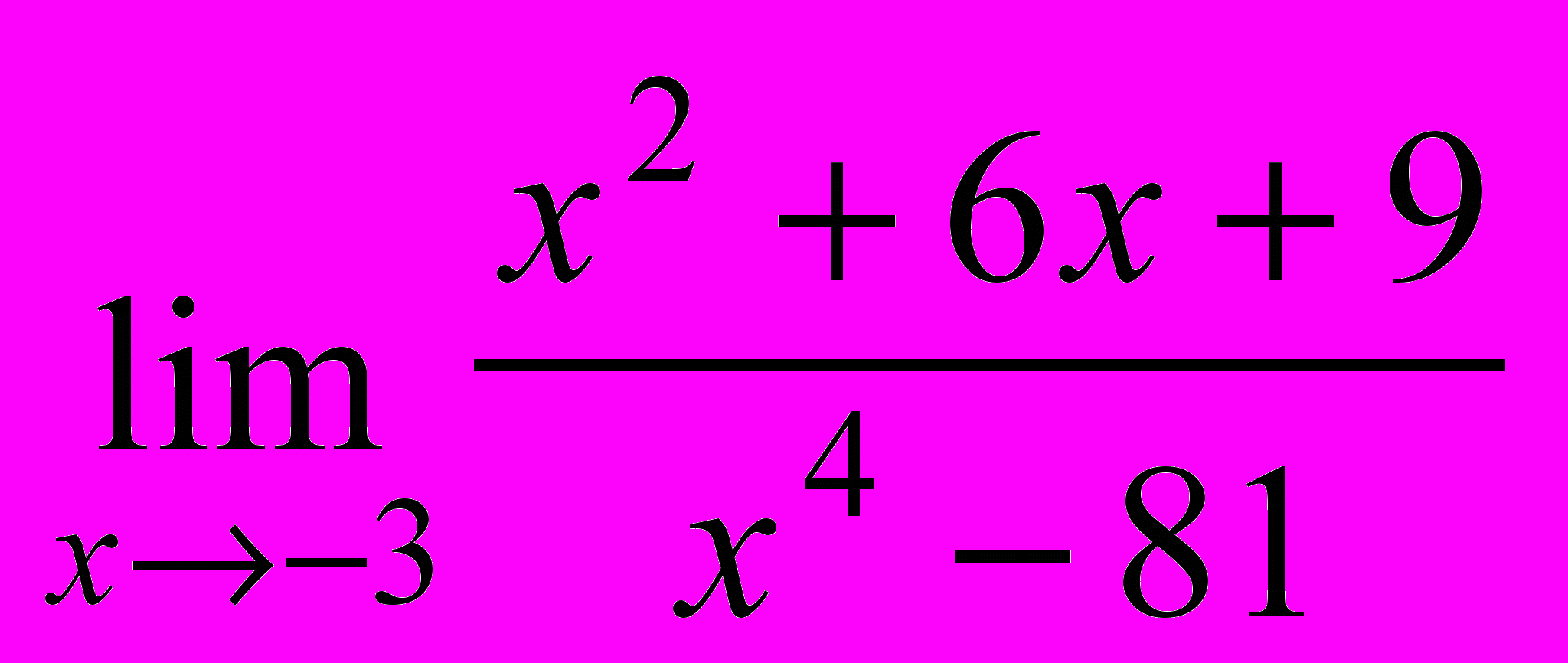
6. Исследовать на непрерывность функцию
   
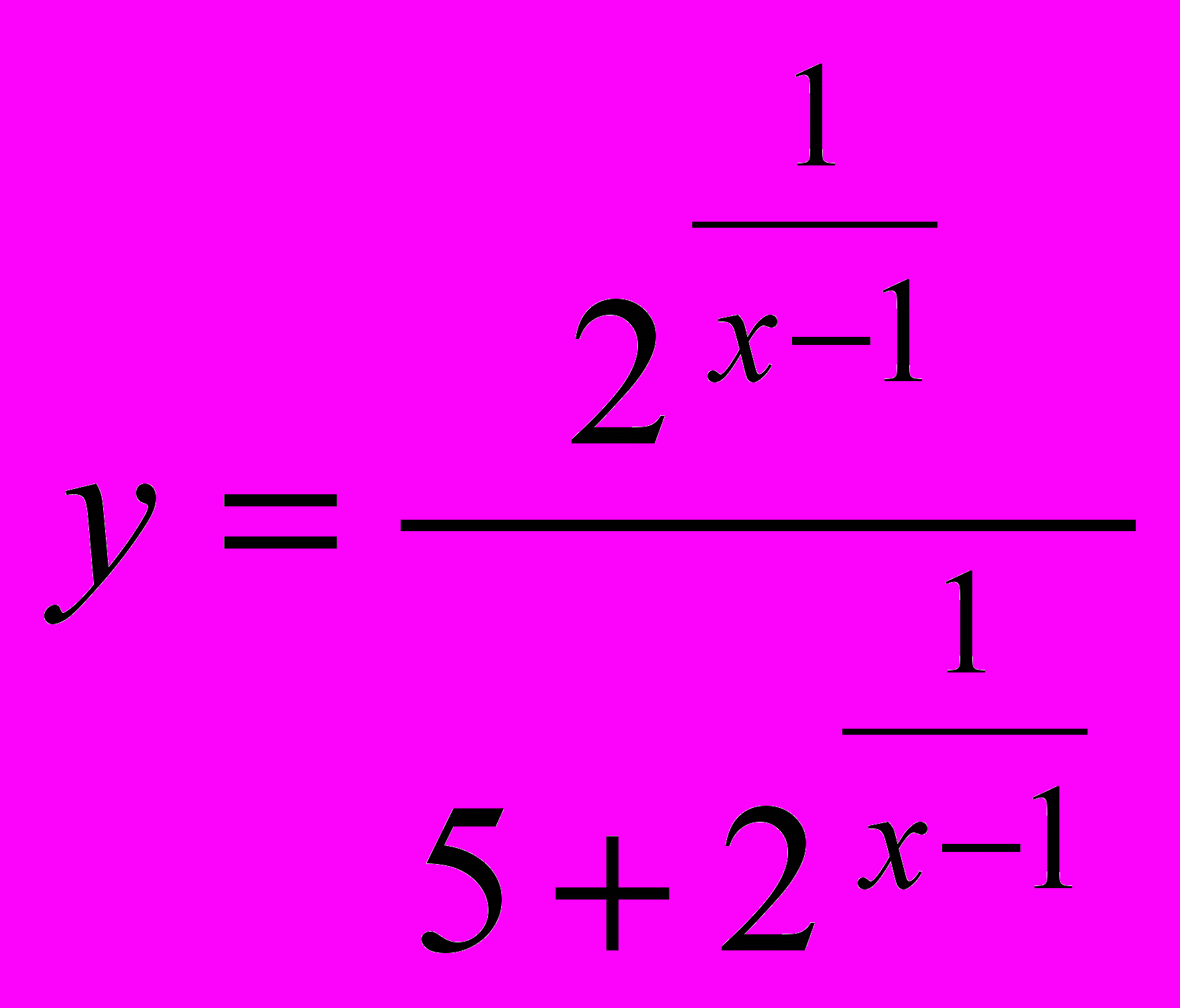
7. Исследовать на экстремум функцию
   
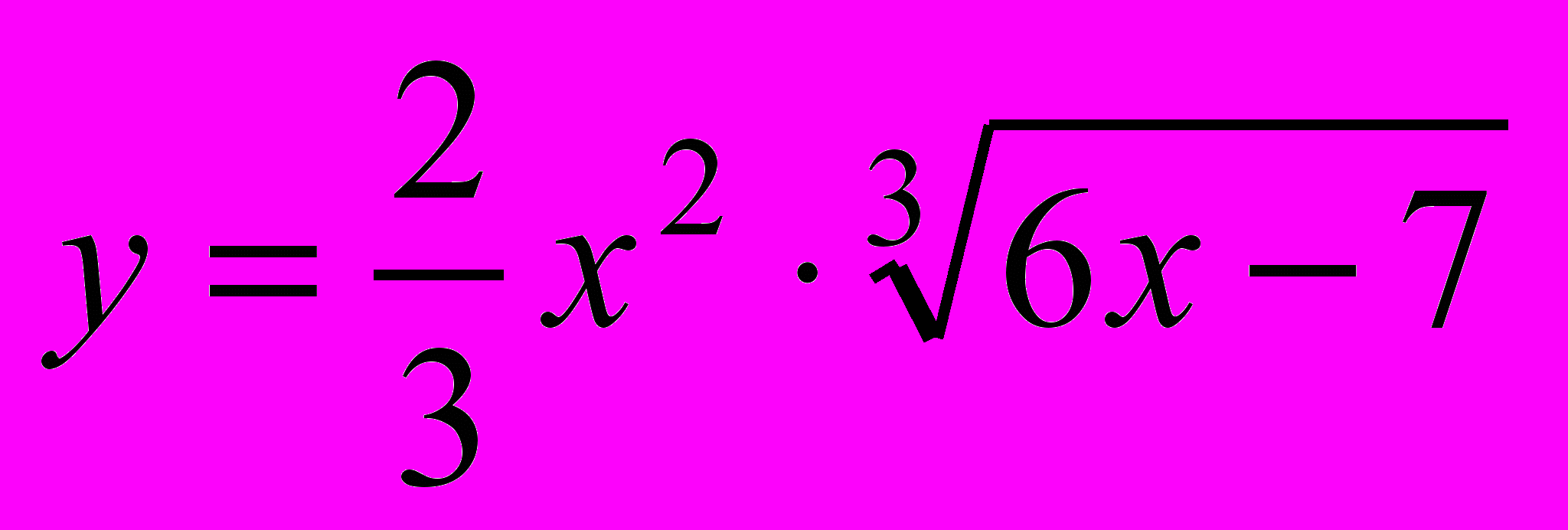
8. Найти значение второй производной функции
   

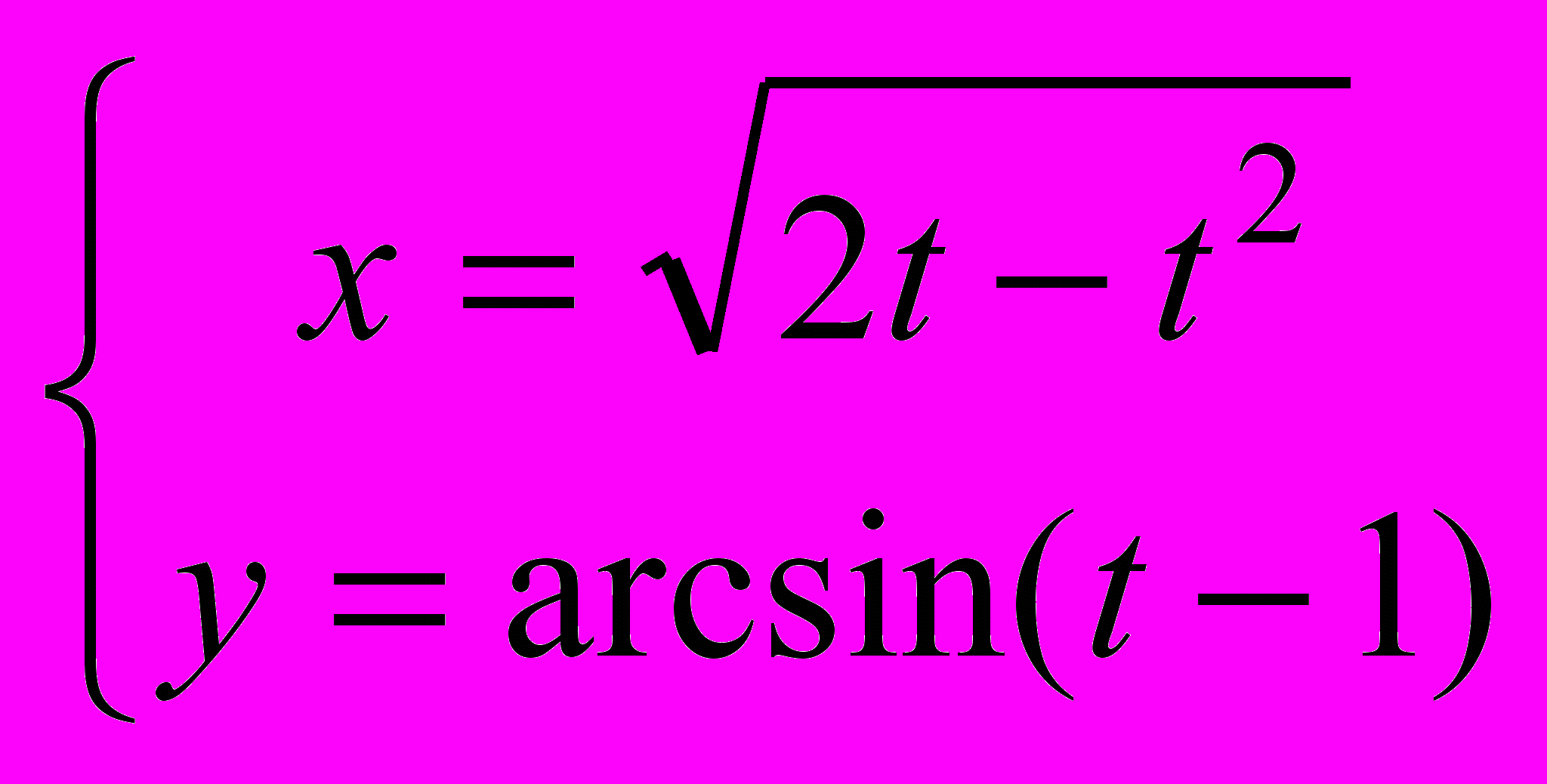
в точке


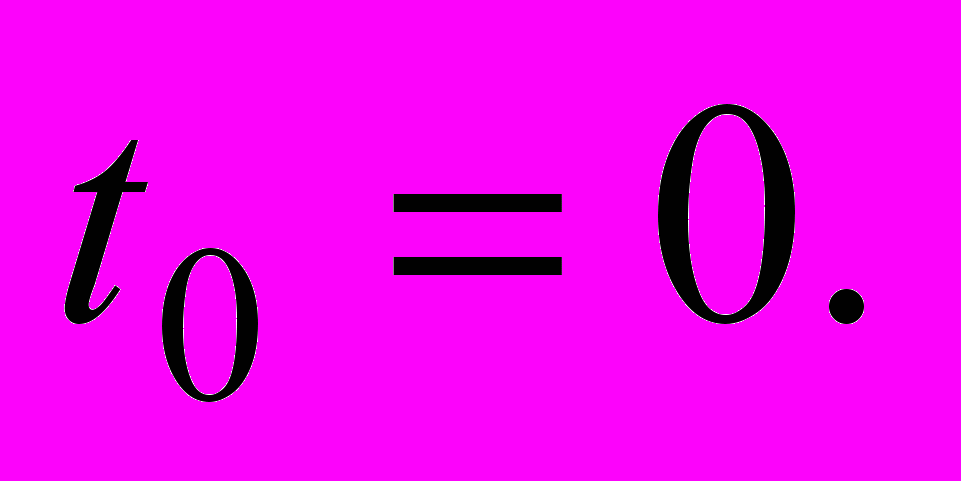
Составил

доцент Терехина Л.И


Утвердил

Зав.кафедрой ВММФ Трифонов А.Ю.


15.12.2008 г.


Экзаменационный билет № 1

Дисциплина:

Высшая математика

Факультет: ФТФ

Курс 1, семестр 2

1. Найти интегралы
   

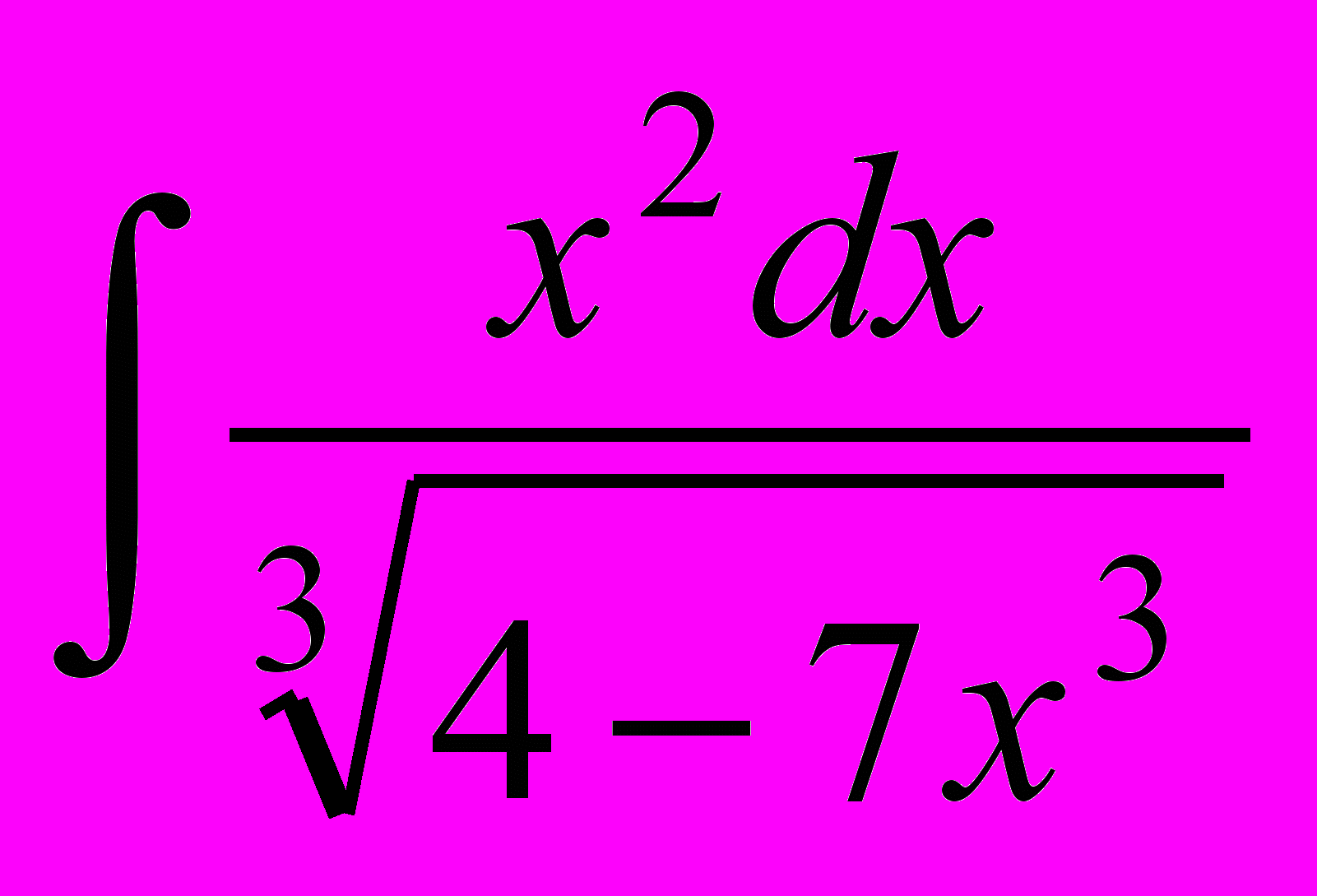
а) б)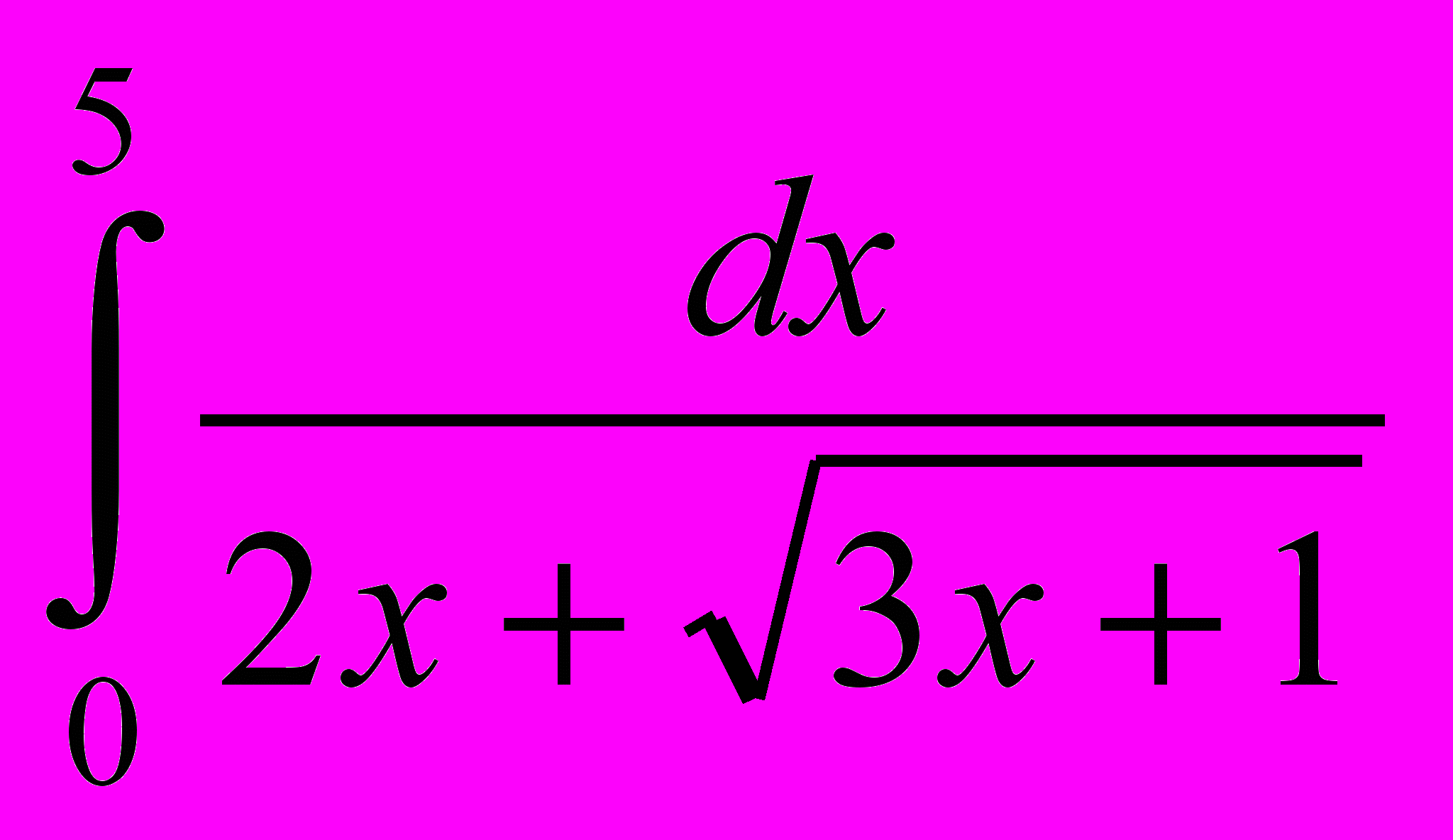


2. Исследовать несобственный интеграл на сходимость

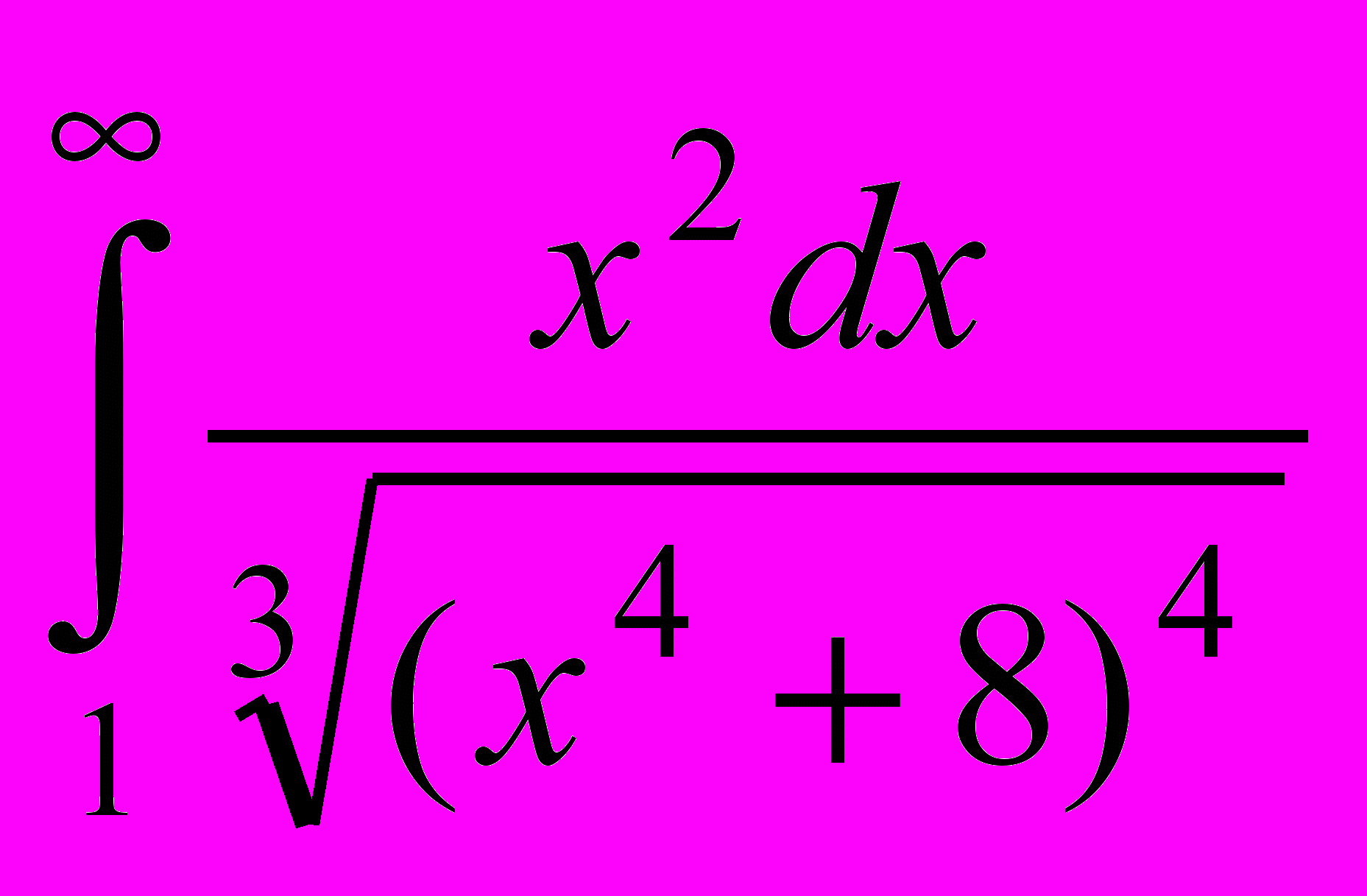
3. Найти объем тела вращения фигуры, ограниченной линиями
   

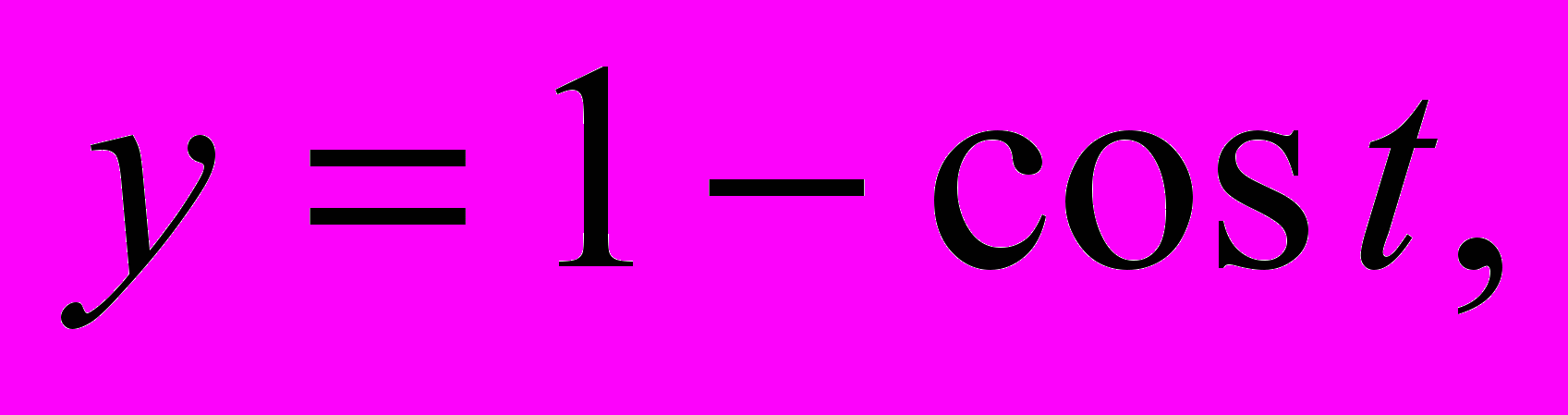
вокруг оси ОХ.


4. Найти производную скалярного поля 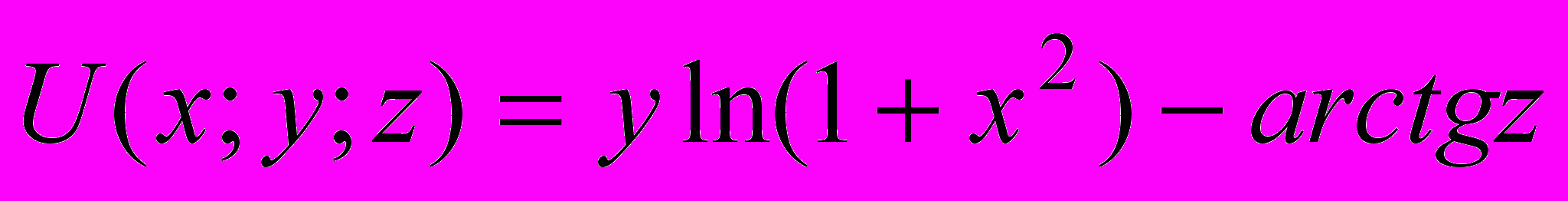в точке 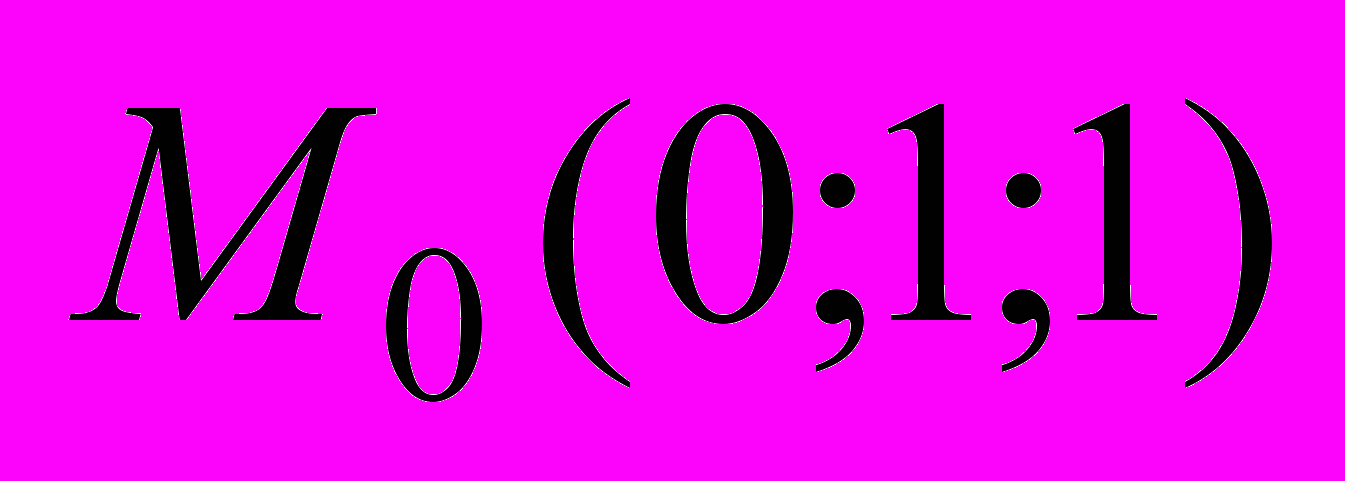в направление вектора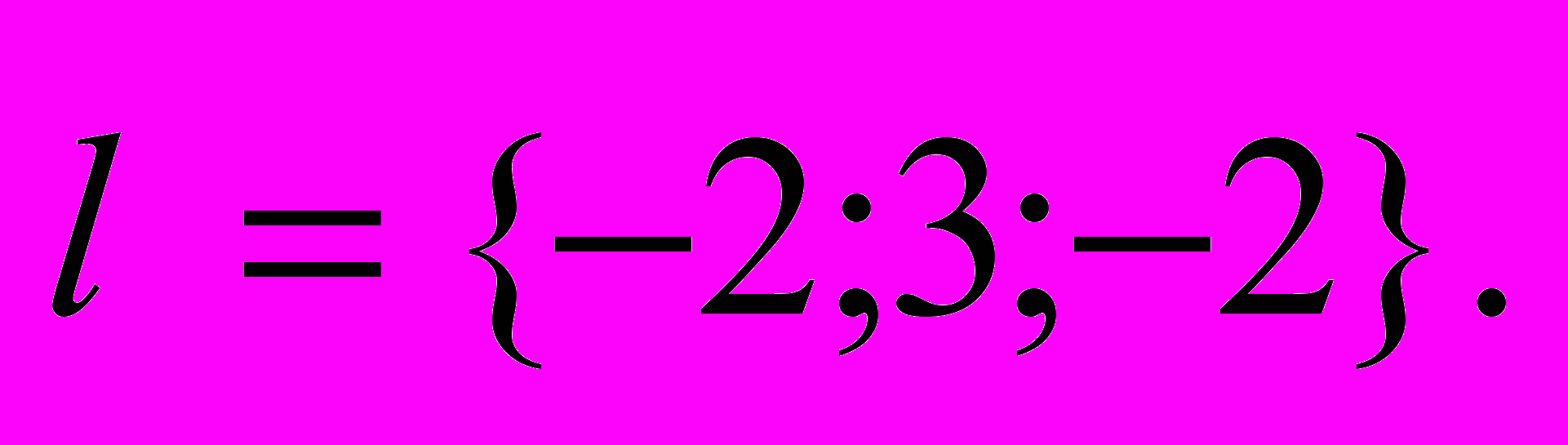


5. Исследовать на сходимость ряд

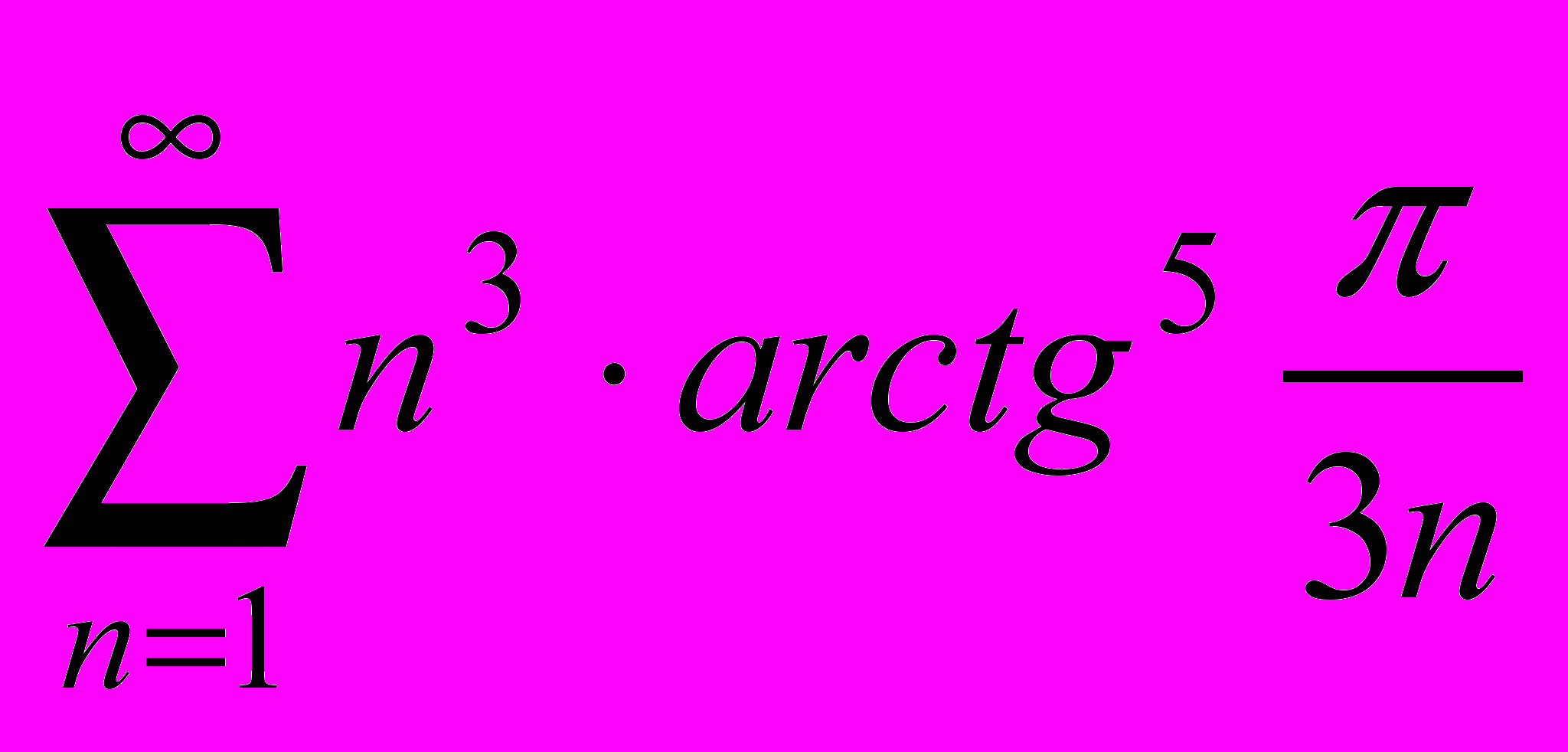
6. Найти интервал сходимости ряда

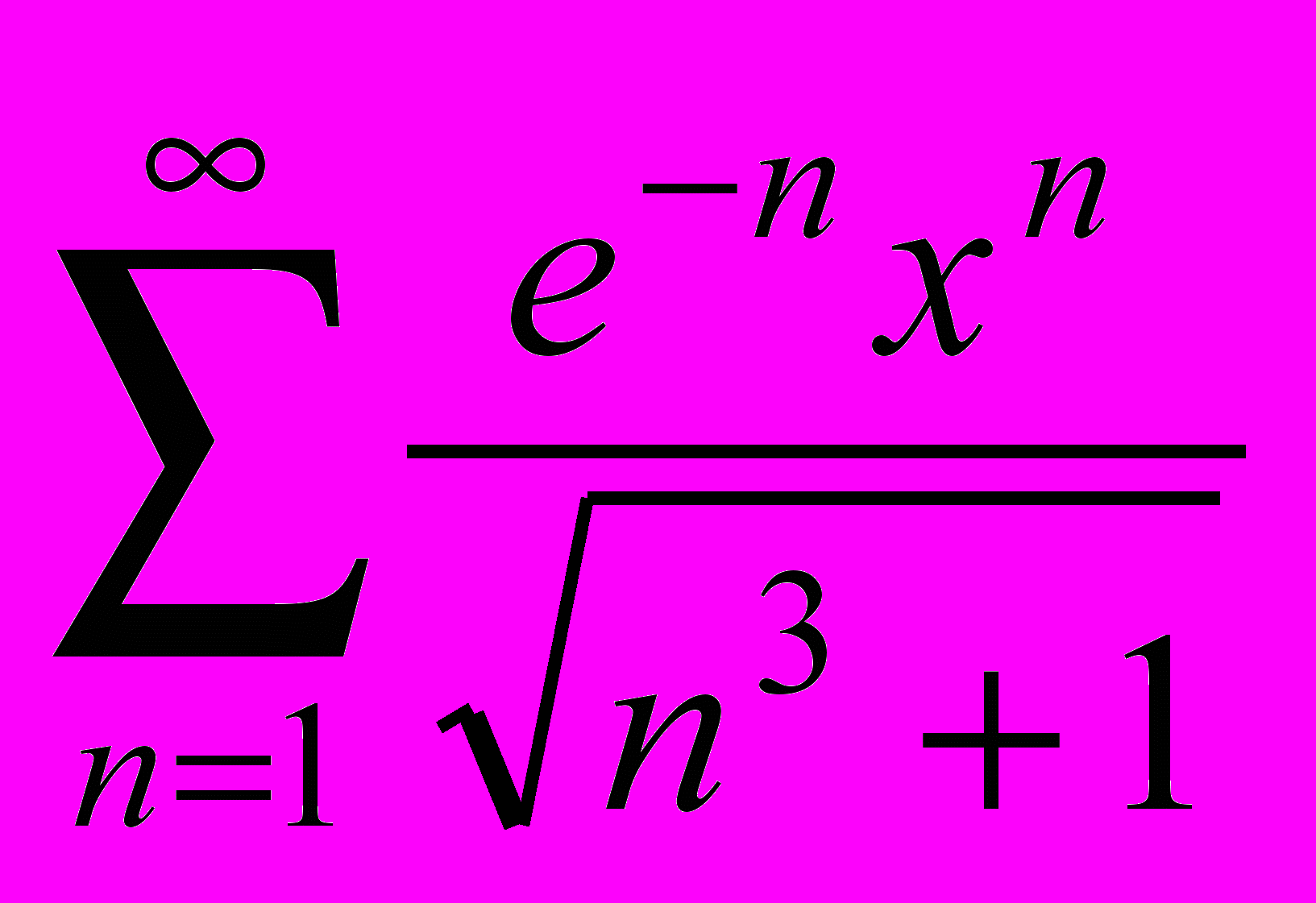
7. Разложить в ряд Маклорена функцию


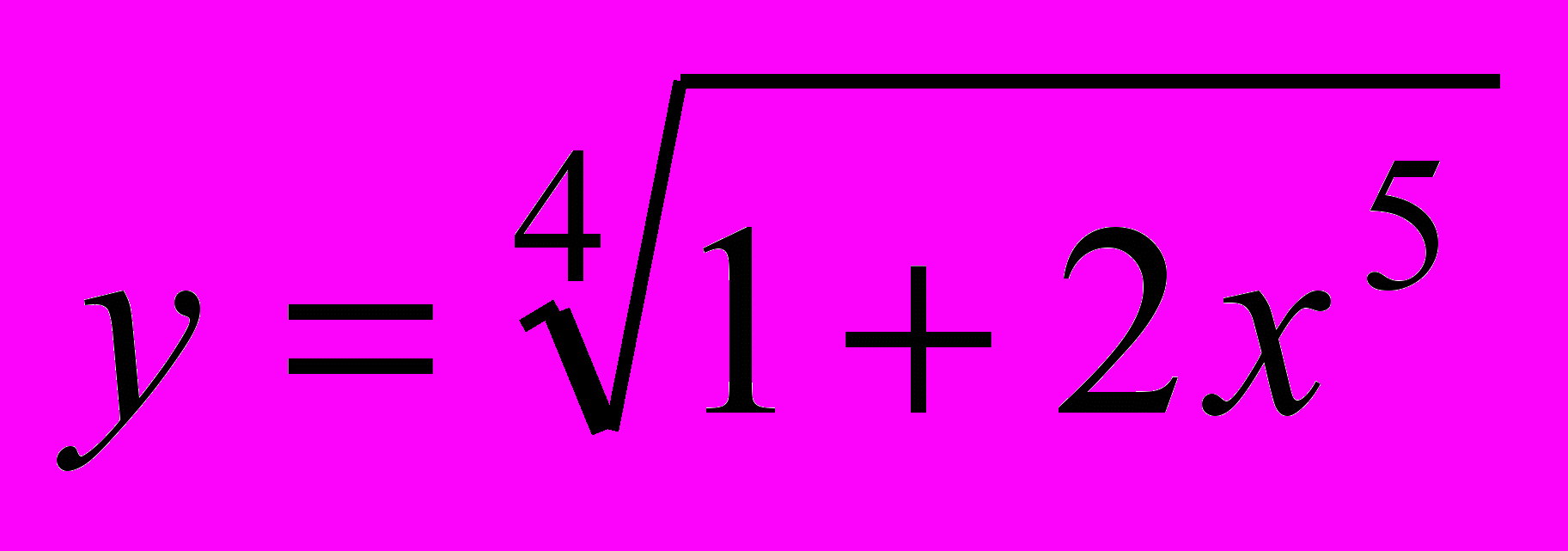
Составил доцент Терехина Л.И

Утвердил

Зав.кафедрой ВММФ Трифонов А.Ю.


01.06.2009 г.


Экзаменационный билет № 1

Дисциплина:

Высшая математика

Факультет: ФТФ

Курс 2, семестр 3


1.Решить уравнения

а)

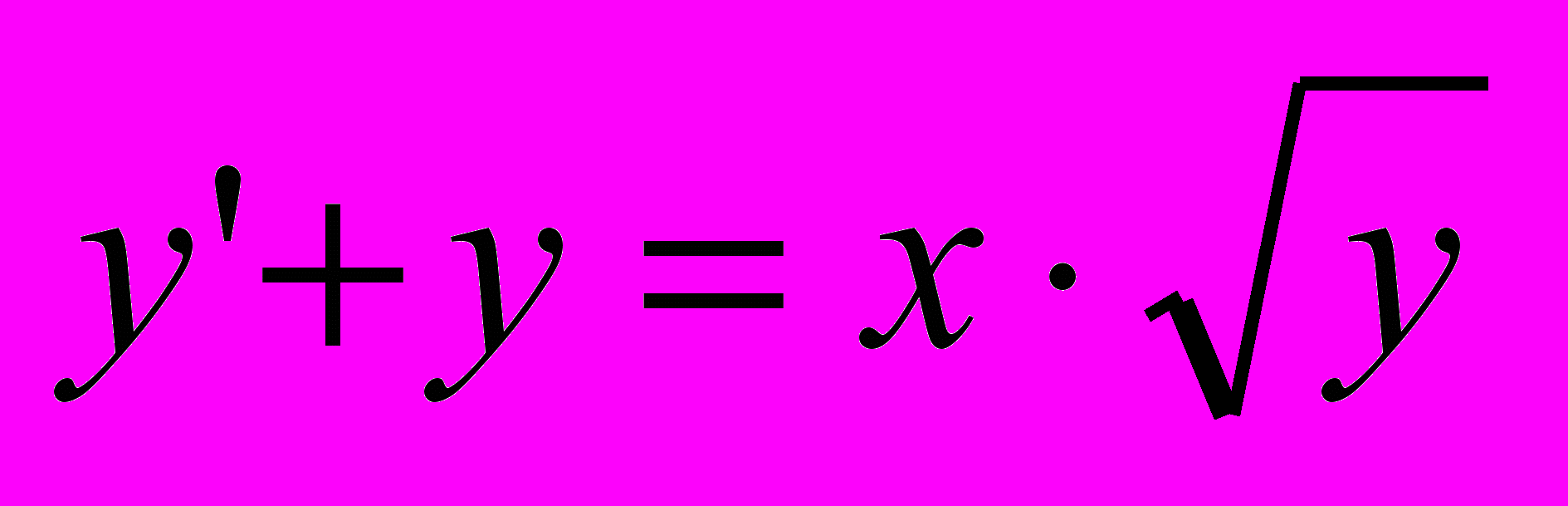
б)

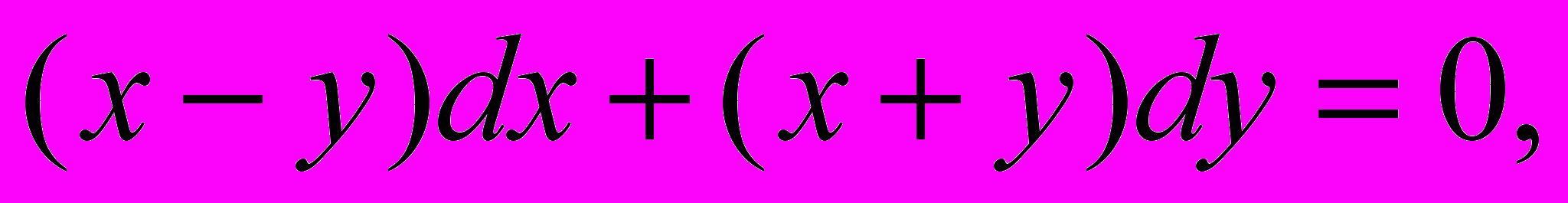
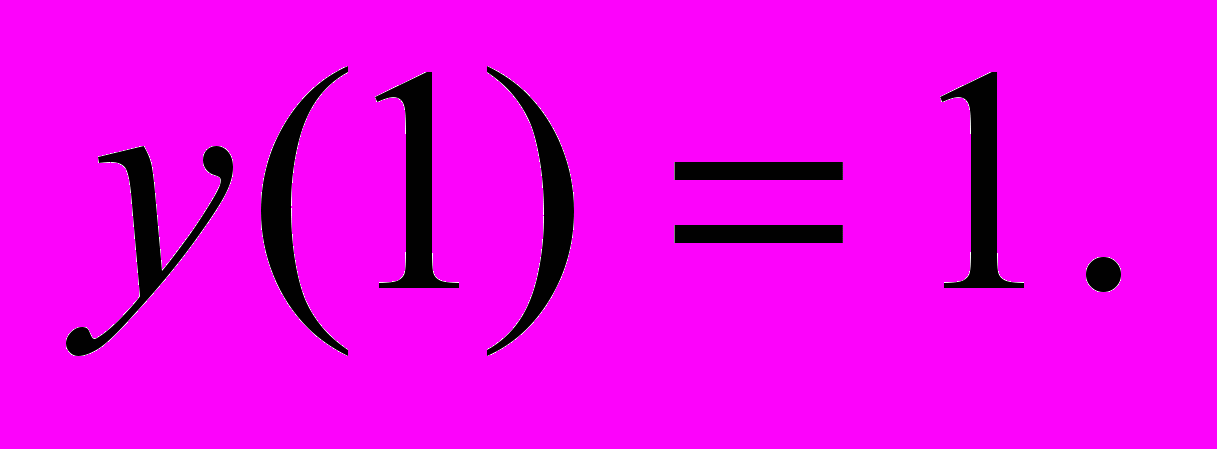
в) ,

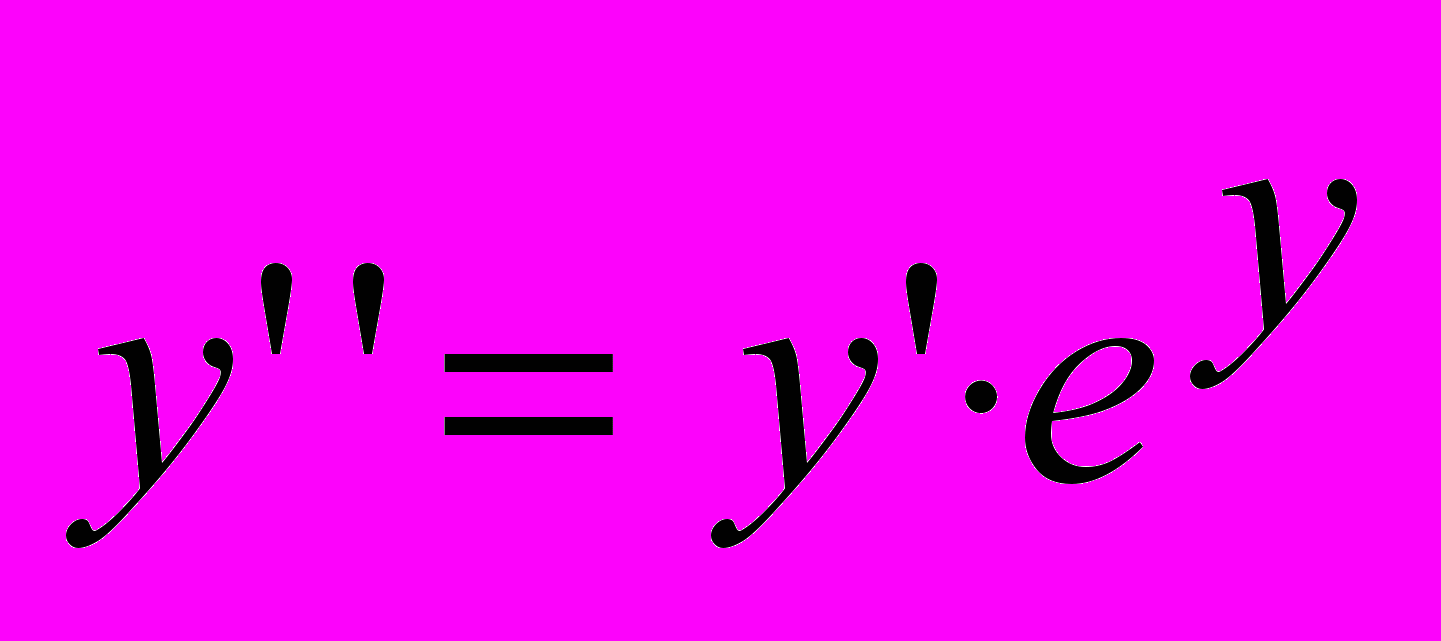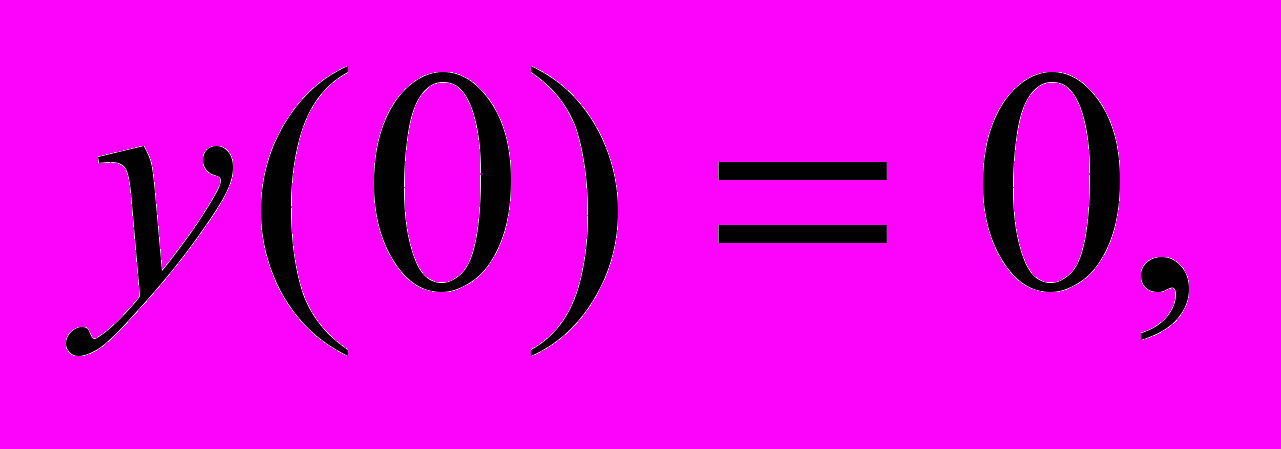
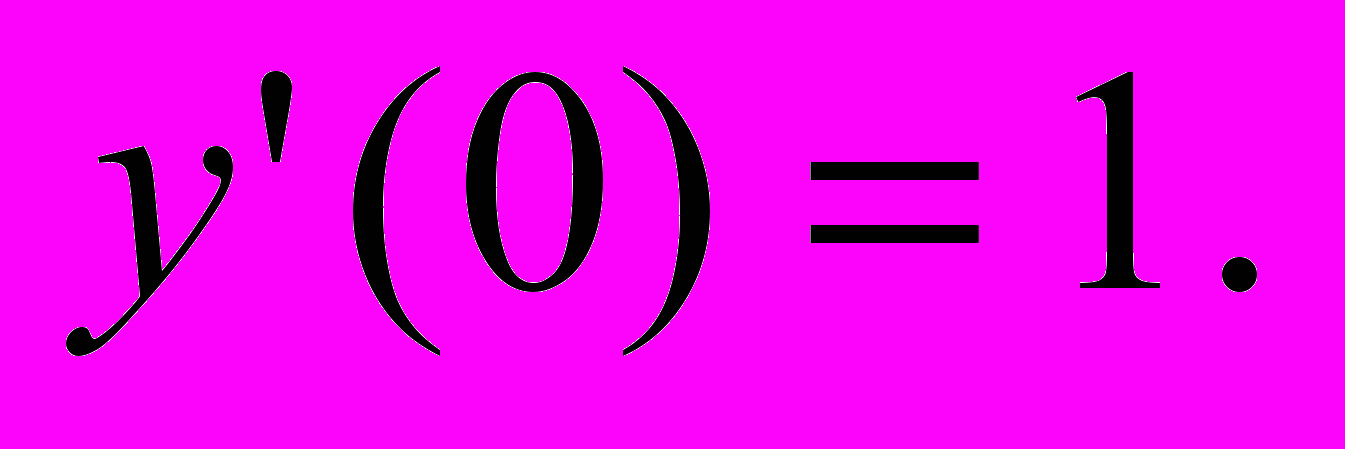
г) .


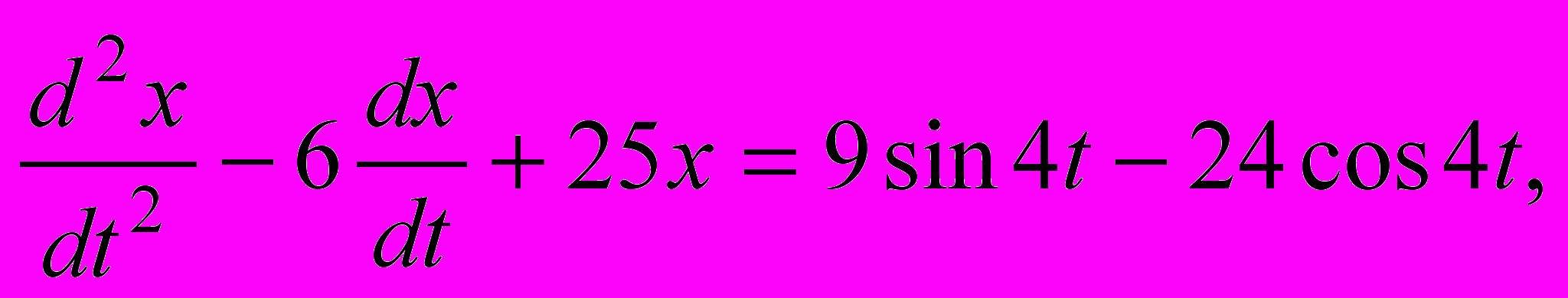
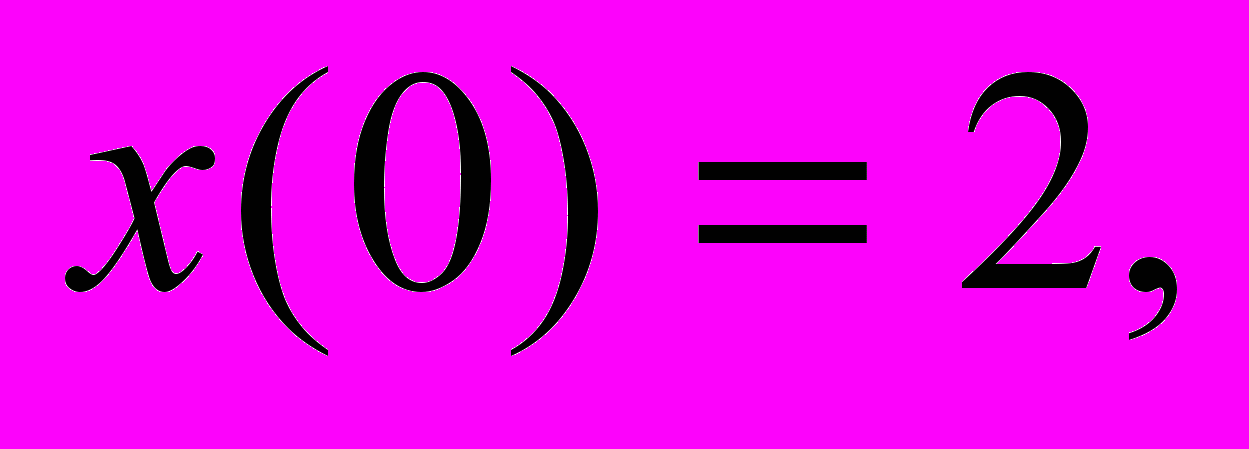
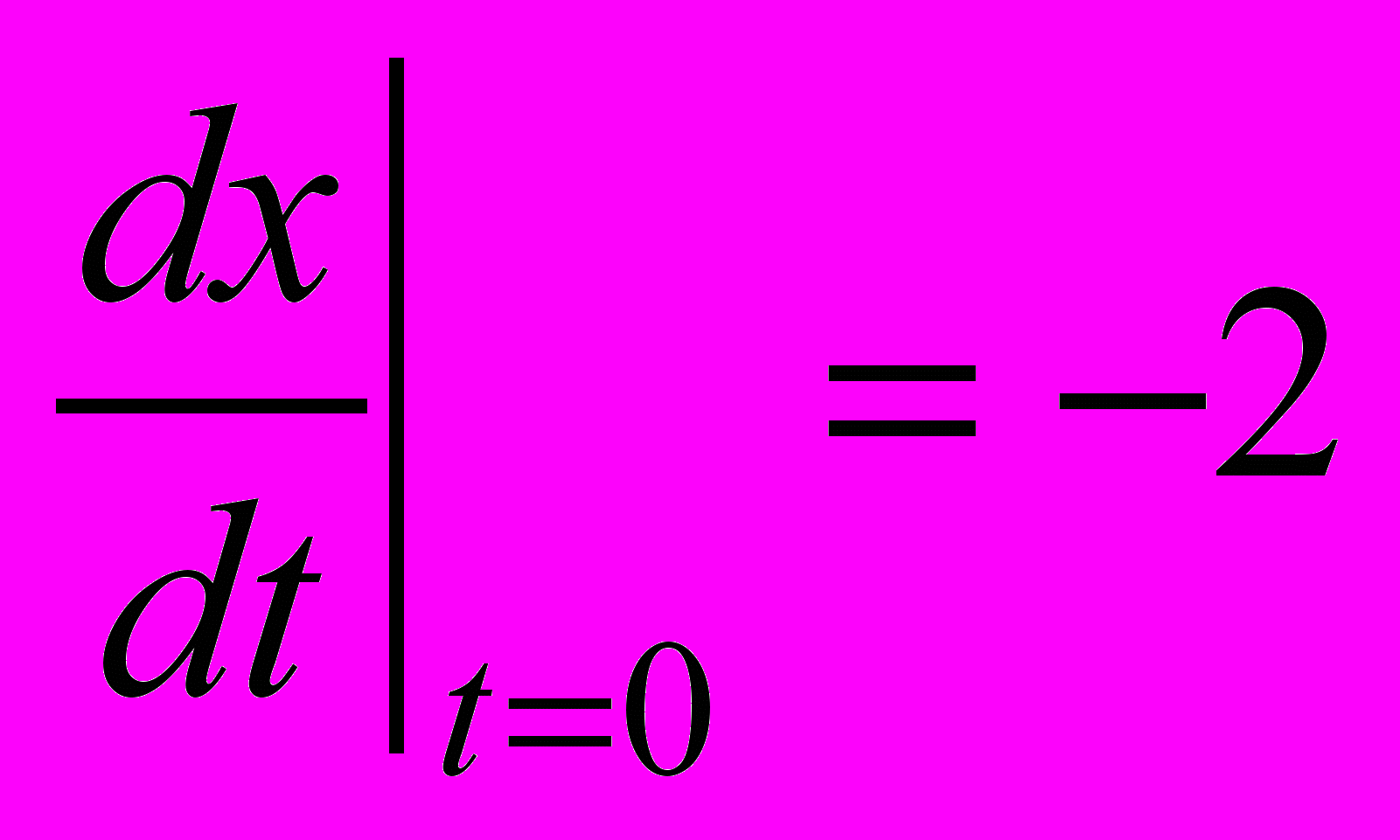2.Вычислить. Результат записать в алгебраической и показательной форме

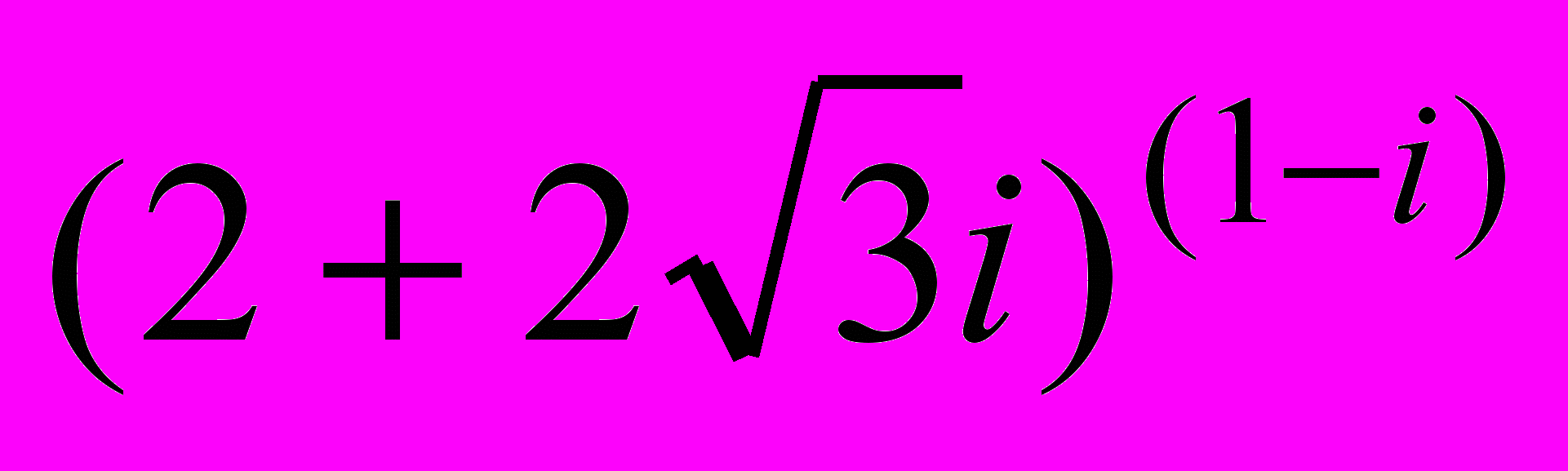а) б) , в)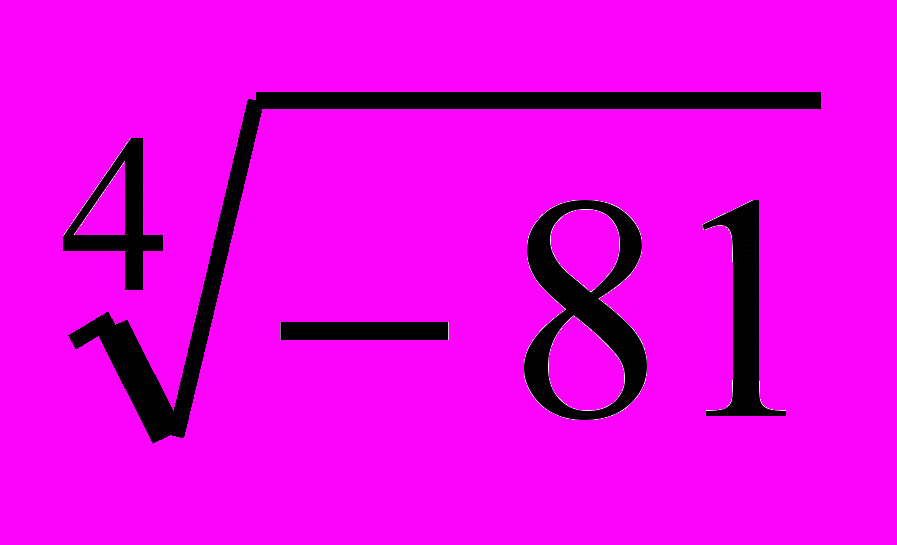


3. Найти коэффициент растяжения и угол поворота комплексной плоскости в точке 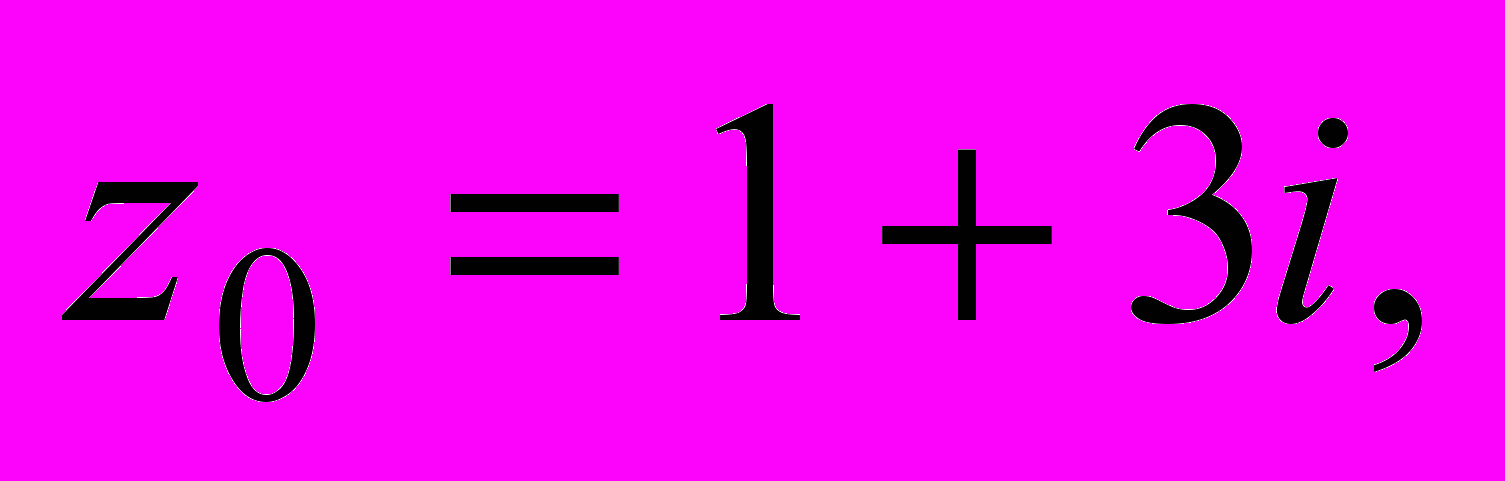при отображении .

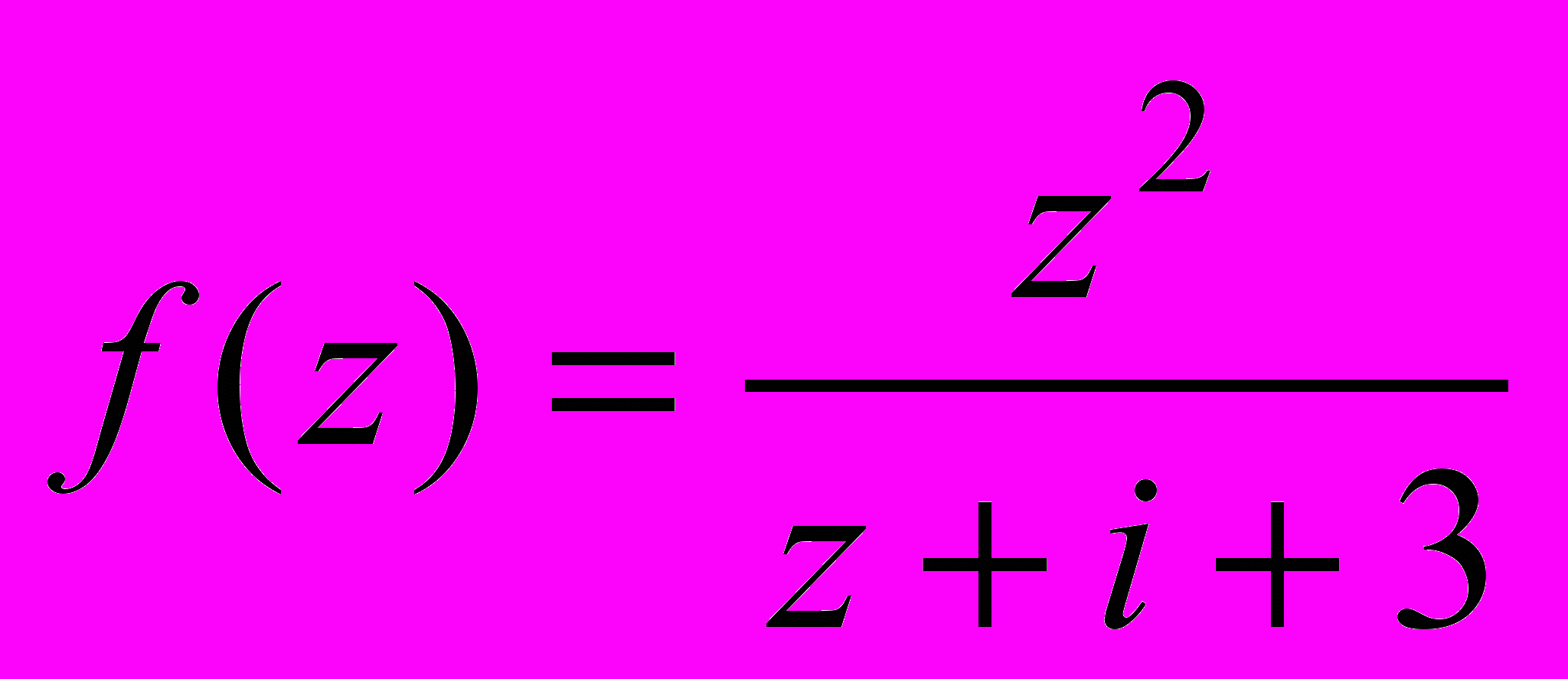4. Вычислить интеграл от функции

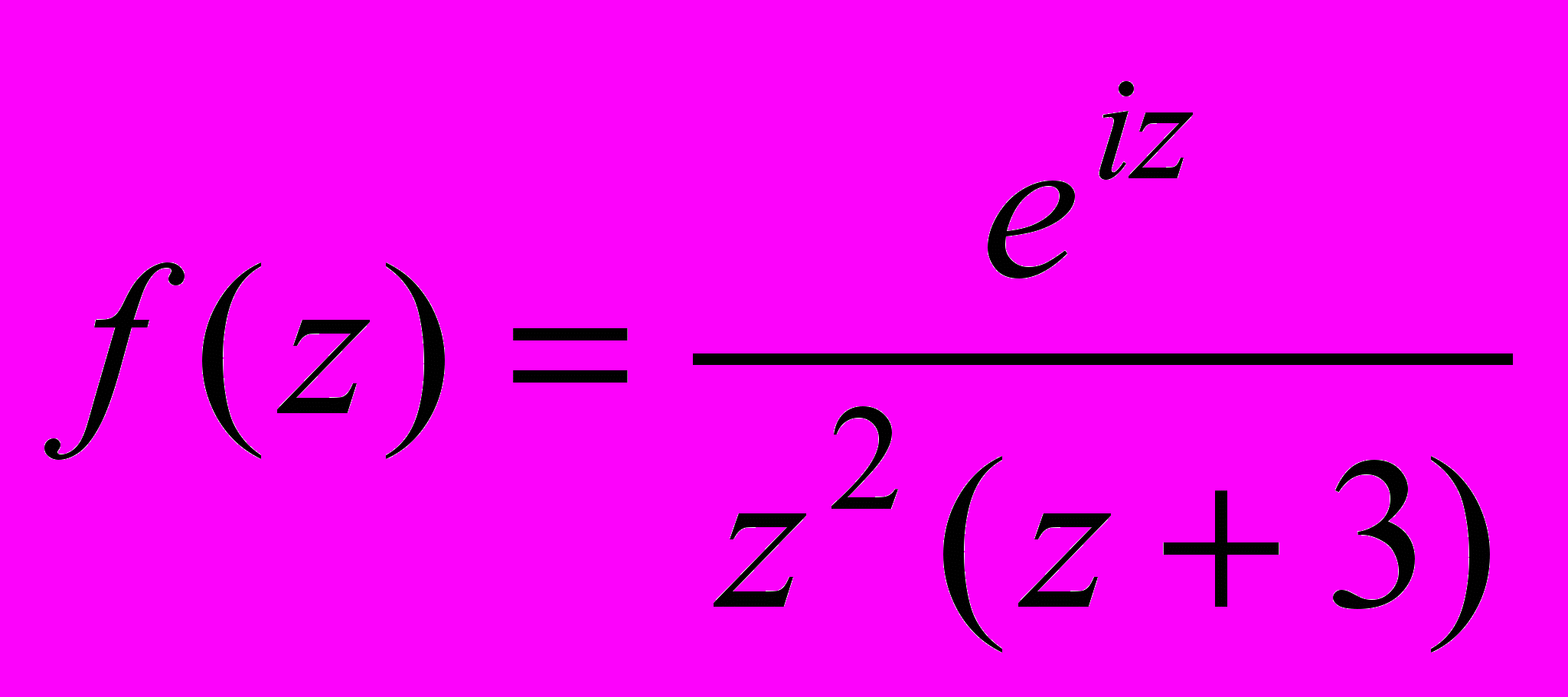
по контуру Г:

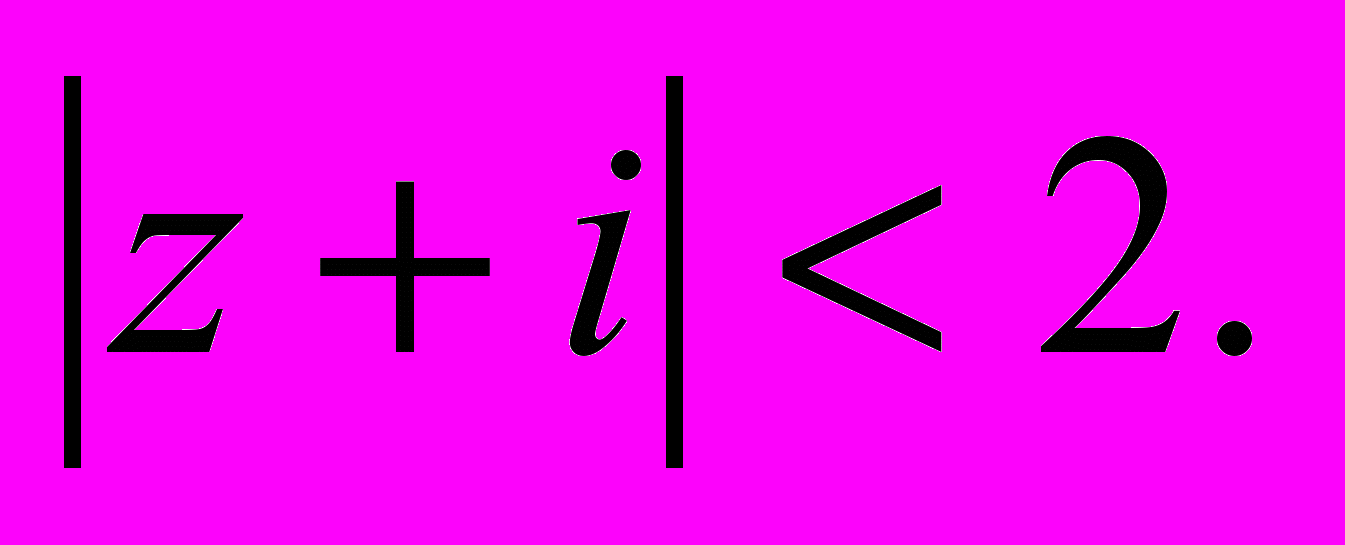
5. Плотность распределения случайной величины Х задана функцией



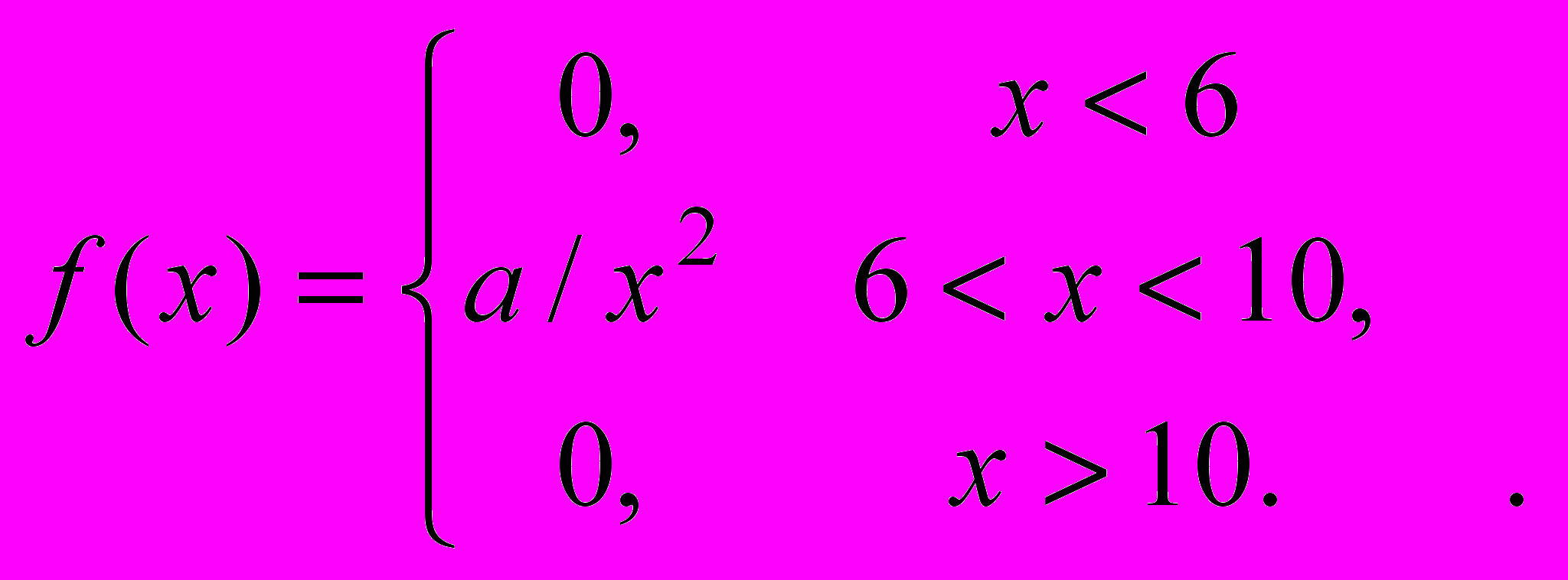
Найти: а) значение параметра “a”,

б) функцию F(х),

в) математическое ожидание М(Х),

г) дисперсию D(Х) случайной величины .

6. Случайная величина распределена нормально с М(Х)=2. Найти дисперсию случайной величины, если известно, что .
   
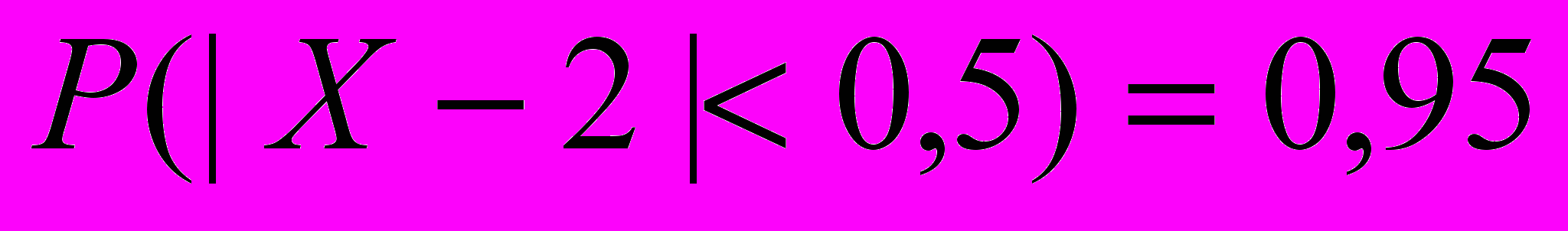7. Собрание, на котором присутствуют 20 человек, в том числе 7 женщин, выбирает делегацию из 5-х человек. Найти вероятность того, что в делегацию войдет 3 женщины и двое мужчин.
   

Составил доцент Терехина Л.И

Утвердил

Зав.кафедрой ВММФ Трифонов А.Ю.