Учебная программа дисциплины экономико-математические модели
| Вид материала | Программа дисциплины |
- Рабочая программа по дисциплине «экономико-математические методы и модели» для специальности, 540.98kb.
- Рабочая программа дисциплины «экономико-математические методы и модели», 129.59kb.
- Программа дисциплины «математические модели в экономике» Для направления, 156.79kb.
- Учебная программа для специальности: ( рабочий вариант) 1-25, 147.69kb.
- Аннотация программы учебной дисциплины в3 Экономико-математические методы и модели, 19.22kb.
- Рабочая программа учебная дисциплина Экономико-математические модели ля студентов очного, 248.59kb.
- Программа дисциплины "Экономико-математические методы и модели в логистических исследованиях", 351.2kb.
- Программа дисциплины «Экономико-математические модели контроллинга на промышленном, 377.56kb.
- Рабочая программа дисциплины «математические модели принятия решений» Рекомендуется, 110.47kb.
- Учебная программа по дисциплине Математические методы и модели в управлении для специальности, 79.82kb.
 | РУКОВОДЯЩИЙ ДОКУМЕНТ Белорусского государственного университета ___________________________________________ | |
| Одобрена Научно-методическим советом Белорусского государственного университета Протокол № от “___” _________ 200 г. | УТВЕРЖДАЮ Ректор Белгосуниверситета профессор Стражев В.И. “______” ____________________ 200 г. |
УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ
МОДЕЛИ
© БГУ (Электронный документ)
Минск
Предисловие
РАЗРАБОТАНА Белорусским государственным университетом
СОСТАВИТЕЛЬ док. ф.-м. наук, проф. П.П. ЗАБРЕЙКО
ИСПОЛНИТЕЛИ:
Алехно Е.А. - кандидат физико-математических, ассистент кафедры математические методы теории управления механико-математического факультета БГУ.
ВНЕСЕНА Кафедрой математические методы теории управления механико-математического факультета БГУ на основе стандартных программ, разработанных соответствующими кафедрами МГУ.
ОДОБРЕНА Научно-методическим советом Белорусского государственного университета (Протокол от № )
2 УТВЕРЖДЕНА И ВВЕДЕНА В ДЕЙСТВИЕ приказом Ректора Белорусского государственного университета от № с 200 г.
3 ВВЕДЕНА ВПЕРВЫЕ
© БГУ (Электронный документ)
Настоящий руководящий документ (учебная программа дисциплины) не может быть тиражирован и распространен без разрешения Белорусского государственного университета
_____________________________________________________________________________
Издан на русском языке
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
За последние 50 лет математические методы в экономике проникли во все области науки. В настоящее время хорошо подготовленный экономист должен владеть многими методами современной математики. Без изучения экономико-математических моделей не обойтись ни специалисту в области экономической теории, ни хозяйственному руководителю, ответственному за выбор решений. Экономико-математические модели – это практический аппарат для анализа экономических процессов.
"ЭКОНОМИК О-МАТЕМАТИЧЕСКИЕ МОДЕЛИ"
Цель курса "Экономико-математические модели": дать возможность студентам познакомиться с основными статическими моделями, используемыми в современной математической экономике, в частности, с классической моделью Леонтьева и ее многочисленными обобщениями. В курсе дается не только описание рассматриваемых моделей и основных утверждений о них, но и полное их обоснование. В этой же связи, излагается ряд математических понятий и результатов играющих существенную роль в математической экономике.
Тематический план курса "Экономико-математические модели"
-
№ темы
Количество часов
Содержание курса
Лекции
КСР
1. Экономика и математика.
4
2. Открытая модель Леонтьева.
8
2
3. Теория неотрицательных матриц.
20
8
4. Обобщенная модель Леонтьева.
8
2
5. Модель Гейгла.
8
2
6. Модели Купманса.
10
2
7. Замкнутые модели.
10
4
8. Некоторые другие модели экономики.
10
4
Всего аудиторных часов
78
24
ИТОГО:
102
1. ЭКОНОМИКА И МАТЕМАТИКА
Математика и экономика. Пространство благ; основные структуры
конечномерного пространства
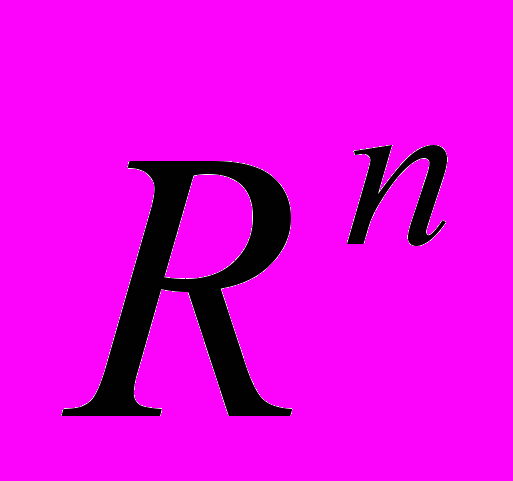с экономической точки зрения. Координатыв "экономических" пространствах; "допустимые" замены переменных. Дуальное пространство с экономической точки зрения. Вещественные и комплексные пространства. Время в экономике. Дискретное и непрерывное время.
Общая схема экономических отношений. Производители и потребители. Рынки.
Статические и динамические модели в экономике.
2. ОТКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕВА
Открытая модель Леонтьева. Уравнение Леонтьева. Производственная матрица.
Экономический смысл элементов, строк и столбцов производственной матрицы.
Неразложимые и разложимые матрицы. Экономический смысл.
Продуктивные открытые модели Леонтьева. Условия продуктивности. Спектральный радиус,
его основные свойства и вычисление. Ряд Неймана.
Объемы производства и потребления. Издержки производства. Прямые и косвенные, суммарные издержки. Основные теоремы об издержках производства в случае неразложимой технологической матрицы и в общем случае.
Феномен Хикса в открытой модели Леонтьева. Случаи неразложимой и разложимых матриц.
Феномен Самуэльсона в открытой модели Леонтьева для неразложимых и разложимых матриц.
Затраты внешних ресурсов. Цены и равновесие в открытой модели Леонтьева. Равновесная и неравновесные экономики.
Обзор условий продуктивности открытой модели Леонтьева.
3. ТЕОРИЯ НЕОТРИЦАТЕЛЬНЫХ МАТРИЦ
Положительные матрицы; геометрический смысл. Теорема Перрона. Спектральные свойства положительных матриц. Теоремы об элементах, "идущих" вперед и назад.
Пространство Биркгофа-Гильберта. Теорема о полноте пространства Биркгофа-Гильберта и теорема Биркгофа. Приложения к задаче о вычислении положительного собственного вектора.
Спектральный зазор положительных матриц. Осцилляция и теорема Островского. Теорема Бауэра. Геометрический смысл теорем Биркгофа, Островского и Бауэра. Оценки спектрального зазора. Теорема Красносельского--Соболева.
Неразложимые матрицы; геометрически смысл неразложимости. Эквивалентные определения неразложимых матриц. Канонические формы разложимых матриц. Теорема единственности. Неразложимость сопряженной матрицы.
Теорема Фробениуса. Теоремы об элементах, "идущих" вперед и назад.
Примитивные матрицы. Спектральные своства примитивных матриц.
Теорема Виландта. Признаки импримитивности неотрицательных матриц.
Острые матрицы и оценки коэффицентов остроты матриц. Импримитивные
матрицы и их спектральные свойства. Теорема об итерациях неразложимых матриц.
Разложимые матрицы; теорема о спектральных свойствах разложимых неотрицательных матриц и теоремы об элементах, "идущих" вперед и назад. Неотрицательные собственные векторы разложимых матриц с максимальным носителем и их нахождение.
Теоремы об оценках спектрального радиуса неотрицательных матриц. Общие теоремы. Итерации разложимых неотрицательных матриц и их асимптотическое поведение. Доказательства теорем Хокинса--Саймона, Хикса и ЛеШателье--Самуэльсона.
4. ОБОБЩЕННАЯ МОДЕЛЬ ЛЕОНТЬЕВА
Обобщенная модель Леонтьева. Сравнение классической и обобщенной моделей Леонтьева.
Издержки производства, прямые и косвенные. Теоремы о положительности издержек.
Цены и равновесные обобщенные модели Леонтьева.
Продуктивные обобщенные модели Леонтьева и основная теорема об условиях продуктивности.
Рыночные обобщенные модели Леонтьева и основная теорема об условиях рыночности.
Обобщенная модель Леонтьева и линейные экстремальные задачи; связь со стандартной и канонической задачами. Теорема Самуэльсона о замещении и ее обобщения. Базисы продуктивности и их геометрическая структура.
5. МОДЕЛЬ ГЕЙЛА
Обобщенная модель Леонтьева и модель Гейла, их сравнение. Издержки
производства, прямые и косвенные. Цены и равновесные обобщенные
модели Леонтьева. Модель Вальраса-Касселя.
Модель Гейла и линейные экстремальные задачи; связь с нормальными
задачами. Продуктивные и рыночные модели Гейла; связь теорем двойственности для линейных экстремальных задач и теорем о продуктивности и рыночности.
Теорема Самуэльсона о замещении и ее обобщения. Базисы продуктивности и их
геометрическая структура.
6. МОДЕЛИ КУПМАНСА
Геометрические описания множеств выпуска в различных моделях.
Постулаты Купманса. Эффективное производство. Теорема об эффективности. Теорема о децентрализации.
Блага и ресурсы. Равновесные и неравновесные модели с благами и ресурсами. Условия продуктивности и рыночности.
Экология и экономические модели. Модель Леонтьева--Форда, ее условия продуктивности. Феномены Хикса и ЛеШателье-Самуэльсона для модели Леонтьева--Форда. Обобщенные модели Леонтьева--Форда.
7. ЗАМКНУТЫЕ МОДЕЛИ
Замкнутая модель Леонтьева. Продуктивность замкнутой модели Леонтьева. Основные теоремы об условиях продуктивности. Затраты внешних ресурсов. Цены и равновесие в замкнутой модели Леонтьева. Равновесная и неравновесные экономики в замкнутой модели Леонтьеваа. Связь между открытой и замкнутой моделями Леонтьева.
Замкнутые обобщенные модели Леонтьева и Гейла и основные результаты о них.
8. НЕКОТОРЫЕ ДРУГИЕ МОДЕЛИ ЭКОНОМИКИ
Понятие о динамических моделях экономики. Динамические модели первого, второго и высшего порядков. Стационарные решения. Магистральные решения и темпы роста развития экономики. Условия существования магистральных решений, характеристические уравнения. Свойства устойчивости стационарных и магистральных решений.
Геометрические модели фон Неймана и Гейла. Теоремы о магистралях для моделей фон Неймана и Гейла.
ЛИТЕРАТУРА
Аллен Р. Математическая экономия. - Москва:
Издательство иностранной литературы, 1963. - 600 с.
Ашманов С.А. Математические модели и методы в
экономике. - Москва: Издательство Московского университета, 1980. - 200 с.
Ашманов С.А. Введение в математическую экономику. -
Москва: Наука, главная редакция физико-математической литературы,
1984. - 294 с.
Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления
(Справочно-математическая библиотека).} - М.: Наука, Главная
редакция физико-математической литературы, 1984. - 320 с.
Гантмахер Ф.Р.} {\it Теория матриц}. - Москва: Наука,
Физматгиз, 1966. - 548 с.
Dorfman R., Samuelson P.A., Solow R.M. Linear
Programming and Economic Analysis. - New York Toronto London:
McGraw-Hill Book Company, Inc., 1958. - 525 с.
Забрейко П.П.it Математические Основы Экономики. -
Лекции, 2002, 1-54.
Забрейко П.П., Шевелевич К.В. Теоремы Хикса и
Ле-Шателье--Самуэльсона для разложимых неотрицательных матриц. -
Доклады НАН Беларуси, (2002), No 3, с. 30-34.
Интрилигатор М. Математические методы оптимизации и
экономическая теория. - Москва: Прогресс, 1975. - 608 с.
Карлин С. Математические методы в теории игр,
программировании и экономике. - Мир, 1964. - 839 с.
Кун Г.У., Таккер А.У. Линейные неравенства и смежные
вопросы. - М.: Издательство иностранной литературы, 1959. - 470 с.
Ланкастер К. Математическая экономика. - Москва:
Советское Радио, 1972. - 464 с.
Сюдсетер К., А., Берк П. Справочник по
математике для экономистов. Санкт-Петербург: Экономическая школа
Санкт-Петербургский государственный университет экономики и
Финансов. Высшая школа экономики, 2000. 1-230
Хорн Р., Джонсон Ч. Матричный анализ. -- М.: Мир,
1989, - 656 с.
Эрроу К.Д., Гурвиц Л., Удзава Х. Исследования по
линейномиу и нелинейному программированию. - М.: Издательство
иностранной литературы, 1962. - 333 с.
Утверждена на заседании кафедры ММТУ
Заведующий кафедрой
математических методов теории управления
профессор В.Г. Кротов
Разработчики:
Кафедра ММТУ ММФ
Белорусского государственного университета
Зав. кафедрой В.Г. Кротов
Согласована:
Главное управление учебной и научно-методической работы
Белорусского государственного университета
Начальник Главного управления Л.М. Хухлындина