Басиковой Марины Фанаульевны по учебному курсу «Математика» 5-6класс, «Алгебра» 7-9 класс, «Алгебра и начала математического анализа» 10-11 класс пояснительная записка

Вид материала

Пояснительная записка

Содержание Использовать приобретенные знания и умения в практической деятельности и повседневной жизни Функции и графики Начала математического анализа Использовать приобретенные знания и умения в практической деятельности и повседневной жизни Уравнения и неравенства Тематическое планирование программы алгебра и начала математического анализа 10 класс. Дата проведения Тригонометрические функции любого угла. 6ч. Основные тригонометрические формулы. 9ч Формулы сложения и их следствия. 7ч Тригонометрические функции числового аргумента. 6ч. Основные свойства функций, 13 ч Решение тригонометрических уравнений и неравенств,13 ч Применение непрерывности и производной, 9 ч Применения производной к исследованию функций, 16 ч Учебно-тренировочные тестовые задания ЕГЭ, 9 ч Пояснительная записка Цели и задачи обучения математики. Место учебного предмета в учебном плане. Обобщение понятия степени (13ч.) ... Полное содержание

Подобный материал:

• Учебника Шабунин М. И., Прокофьев А. А. «Математика. Алгебра. Начала математического, 133.96kb.
• Календарно-тематическое планирование Алгебра и начала математического анализа, 10 класс, 478.94kb.
• А. Н. Колмогорова и др. «Алгебра и начала анализа», 10 класс (профильный уровень) Пояснительная, 204.68kb.
• Пояснительная записка по предмету «Алгебра и начала анализа», 102.48kb.
• Курс: 3 Семестр: 6 Перечень вопросов к зачету: Частная методика ( математика, алгебра,, 29.41kb.
• Рабочая программа по алгебре основное общее образование, 7 класс базовый уровень, 544.75kb.
• А. Н. Колмогорова и др. «Алгебра и начала анализа», 10 класс (профильный уровень) Составители:, 205.14kb.
• Рабочая программа педагога шашаевой татьяны георгиевны, II квалификационная категория, 400.13kb.
• Кунаревой Арины Вячеславовны по учебному курсу «Алгебра и начала анализа» 10-11 класс, 408.51kb.
• Ячменевой Людмилы Васильевны учителя первой квалификационной категории по изучению, 348.11kb.

Алгебра

Уметь

• выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
  
• проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
  
• вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
  

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
  

Функции и графики

Уметь

• определять значение функции по значению аргумента при различных способах задания функции;
  
• строить графики изученных функций;
  
• описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
  
• решать уравнения, простейшие системы уравнений, используя их графики;
  

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
  

Начала математического анализа

Уметь

• вычислять производные элементарных функций, используя справочные материалы;
  
• исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов с использованием аппарата математического анализа.
  

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• решения прикладных, в том числе социально-экономических и физических, задач на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
  

Уравнения и неравенства

Уметь

• решать рациональные, показательные и логарифмические уравнения и неравенства;
  
• составлять уравнения по условию задачи;
  
• использовать для приближенного решения уравнений и неравенств графический метод;
  
• изображать на координатной плоскости множества решений простейших уравнений и их систем.
  

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• построения и исследования простейших математических моделей.
  

Тематическое планирование программы алгебра и начала математического анализа 10 класс.

№ урока	Тема урока		Дата проведения		Примечание
			По плану	фактически
	Тригонометрические функции любого угла. 6ч.
1	Определение синуса, косинуса, тангенса и котангенса
2	Определение синуса, косинуса, тангенса и котангенса
3	Свойства синуса, косинуса, тангенса и котангенса
4	Свойства синуса, косинуса, тангенса и котангенса
5	Радианная мера угла
6	Радианная мера угла
	Основные тригонометрические формулы. 9ч
7	Соотношения между тригонометрическими функциями одного и того же угла.
8	Соотношения между тригонометрическими функциями одного и того же угла.
9	Применение основных тригонометрических формул к преобразованию выражений.
10	Применение основных тригонометрических формул к преобразованию выражений.
11	Применение основных тригонометрических формул к преобразованию выражений.
12	Применение основных тригонометрических формул к преобразованию выражений.
13	Формулы приведения
14	Формулы приведения
15	Контрольная работа №1 по теме « Основные тригонометрические формулы»
	Формулы сложения и их следствия. 7ч
16	Формулы сложения
17	Формулы сложения
18	Формулы двойного угла
19	Формулы двойного угла
20	Сумма и разность тригонометрических функций
21	Сумма и разность тригонометрических функций
22	Сумма и разность тригонометрических функций
	Тригонометрические функции числового аргумента. 6ч.
23	Практикум по решению задач на использование тригонометрических формул
24	Практикум по решению задач на использование тригонометрических формул
25	Тригонометрические функции и их графики.
26	Тригонометрические функции и их графики.
27	Тригонометрические функции и их графики.
28	Контрольная работа №2 по теме «Тригонометрические функции числового аргумента»
	Основные свойства функций, 13 ч
29	Анализ контрольной работы. Функции и их графики
30	Преобразования графиков
31	Четные и нечетные функции.
32	Периодичность тригонометрических функций.
33	Возрастание и убывание функций. Экстремумы.
34	Возрастание и убывание функций. Экстремумы.
35	Исследование функций.
36	Исследование функций.
37	Исследование функций.
38	Исследование функций.
39	Свойства тригонометрических функций. Гармонические колебания
40	Свойства тригонометрических функций. Гармонические колебания
41	Контрольная работа №3 по теме «Основные свойства функций»
	Решение тригонометрических уравнений и неравенств,13 ч
42	Анализ контрольной работы. Арксинус, арккосинус и арктангенс.
43	Арксинус, арккосинус и арктангенс.
44	Решение простейших тригонометрических уравнений.
45	Решение простейших тригонометрических уравнений.
46	Решение простейших тригонометрических уравнений.
47	Решение простейших тригонометрических неравенств.
48	Решение простейших тригонометрических неравенств.
49	Примеры решения тригонометрических уравнений и систем уравнений
50	Примеры решения тригонометрических уравнений и систем уравнений
51	Примеры решения тригонометрических уравнений и систем уравнений
52	Примеры решения тригонометрических уравнений и систем уравнений
53	Примеры решения тригонометрических уравнений и систем уравнений
54	Контрольная работа №4 по теме «Решение тригонометрических уравнений и систем»
	Производная, 14 ч
55	Анализ контрольной работы. Приращение функции
56	Приращение функции
57	Понятие о производной
58	Понятие о непрерывности и предельном переходе.
59	Понятие о непрерывности и предельном переходе.
60	Правила вычисления производных.
61	Правила вычисления производных.
62	Правила вычисления производных.
63	Правила вычисления производных.
64	Производная сложной функции.
65	Производная тригонометрических функций.
66	Производная тригонометрических функций.
67	Производная тригонометрических функций.
68	Контрольная работа № 5 по теме «Производная»
	Применение непрерывности и производной, 9 ч
69	Анализ контрольной работы. Применение непрерывности.
70	Метод интервалов
71	Метод интервалов
72	Касательная к графику функции.
73	Касательная к графику функции.
74	Касательная к графику функции.
75	Приближенные вычисления.
76	Производная в физике и технике.
77	Производная в физике и технике.
	Применения производной к исследованию функций, 16 ч
78	Признак возрастания (убывания) функции.
79	Признак возрастания (убывания) функции.
80	Признак возрастания (убывания) функции.
81	Признак возрастания (убывания) функции.
82	Критические точки функции, максимумы и минимумы.
83	Критические точки функции, максимумы и минимумы.
84	Критические точки функции, максимумы и минимумы.
85	Примеры применения производной к исследованию функции.
86	Примеры применения производной к исследованию функции.
87	Примеры применения производной к исследованию функции.
88	Примеры применения производной к исследованию функции.
89	Наибольшее и наименьшее значение функции
90	Наибольшее и наименьшее значение функции
91	Наибольшее и наименьшее значение функции
92	Наибольшее и наименьшее значение функции
93	Контрольная работа № 6 по теме «Применения производной к исследованию функций»
	Учебно-тренировочные тестовые задания ЕГЭ, 9 ч
94	Преобразование тригонометрических выражений
95	Тригонометрические уравнения
96	Тригонометрические уравнения
97	Наибольшее и наименьшее значение функции
98	Наибольшее и наименьшее значение функции
99	Решение неравенств
100	Решение неравенств
101	Итоговая контрольная работа
102	Итоговая контрольная работа

Учебно-методическая литература для учителя

1.Колмогоров А. Н.и др. Алгебра и начала анализа. 10-11. М.: Просвещение, 2005. 2.Б.М.Ивлев и др. Дидактические материалы по алгебре и началам анализа для 10 класса 3.Б.М.Ивлев и др. Дидактические материалы по алгебре и началам анализа для 10 класса. - М: Просвещение, 2007. 4.Афанасьева Т.Л. и др. Алгебра и начала анализа , 10 класс: Поурочные планы по учебнику А.Н.Колмогорова и др.Волгоград: Учитель, 2008


Пояснительная записка

Программа по алгебре и началам анализа для 10, 11 классов составлена на основе примерной программы среднего (полного) общего образования по математике, федерального компонента государственного стандарта среднего (полного) общего образования на базовом уровне.

Цели и задачи обучения математики.

Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:

      формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

       развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;

      овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;

       воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.

Задачи:

• систематизация сведений о числах;
  
• изучение новых видов числовых выражений и формул;
  
• совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
  
• расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
  
• развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
  
• знакомство с основными идеями и методами математического анализа.
  

Место учебного предмета в учебном плане.

Программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса. В ней приводится распределение учебного времени между разделами курса, представленное в виде тематического планирования, согласно учебнику Колмогорова А.Н для 10-11 классов «Алгебра и начала анализа» общеобразовательных учреждений.

Рабочая программа рассчитана на 102 часа, 3ч в неделю в течение года.

Содержание программы.

Учебно-тематический план 11 класс.

№ п/п	Наименование разделов и тем	Всего ча­сов
1.	§ 9. Обобщение понятия степени.	13
2.	§ 10. Показательная и логарифмическая функции.	18
3.	§ 7. Первообразная.	9
4	§ 8. Интеграл.	10
5	§ 11. Производная показательной и логарифмической функции.	16
7	Обобщающее повторение курса алгебры и начала анализа	36
	Итого:	102

Обобщение понятия степени (13ч.)

Цели: познакомить учащихся с понятия корня n-й степени и степени с рациональным по­казателем, которые являются обобщением понятий квадратного корня и степени с целым показателем. Следует обратить внимание учащихся на то, что рассматриваемые здесь свойства корней и сте­пеней с рациональным показателем аналогичны тем свойст­вам, которыми обладают изученные ранее квадратные корни и степени с целыми показателями. Необходимо уделить доста­точно времени отработке свойств степеней и формированию навыков тождественных преобразований.

Формирование представлений корня n-ой степени из действительного числа, функции 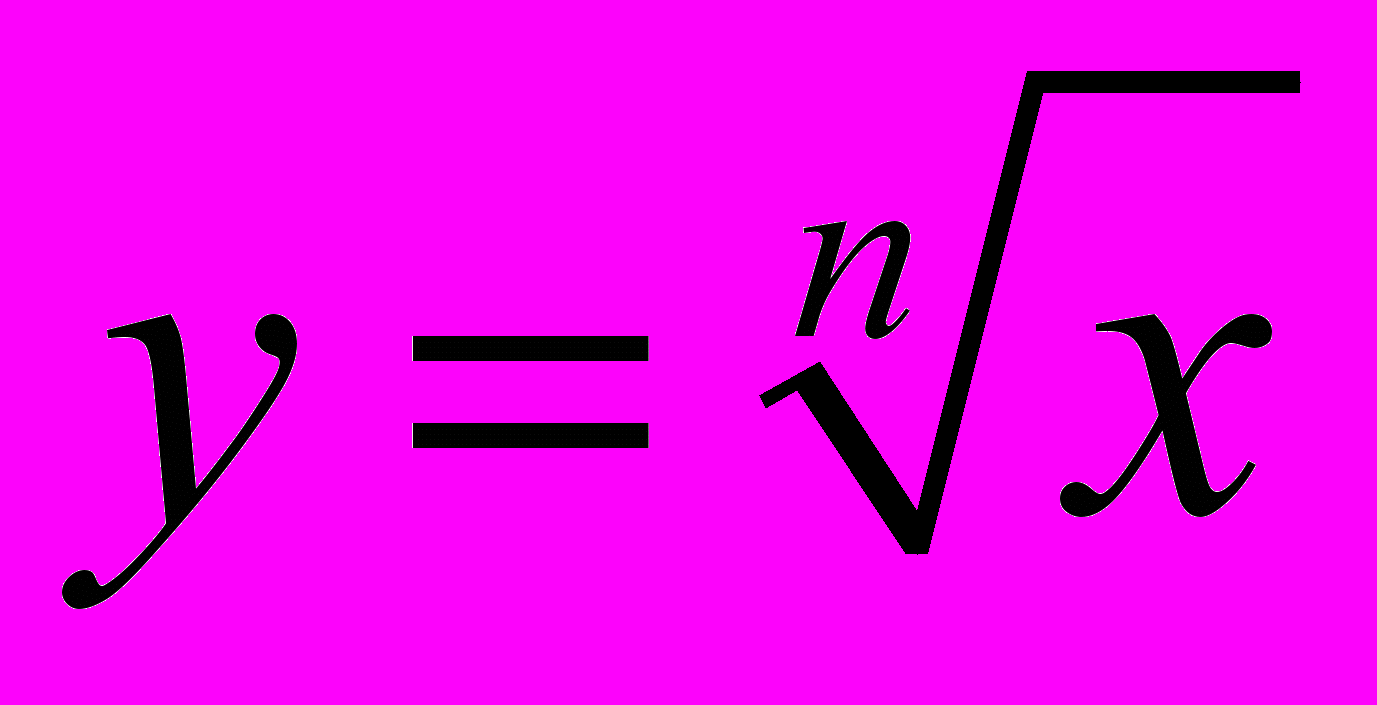и графика этой функции.

Овладение умением извлечения корня, построения графика функции 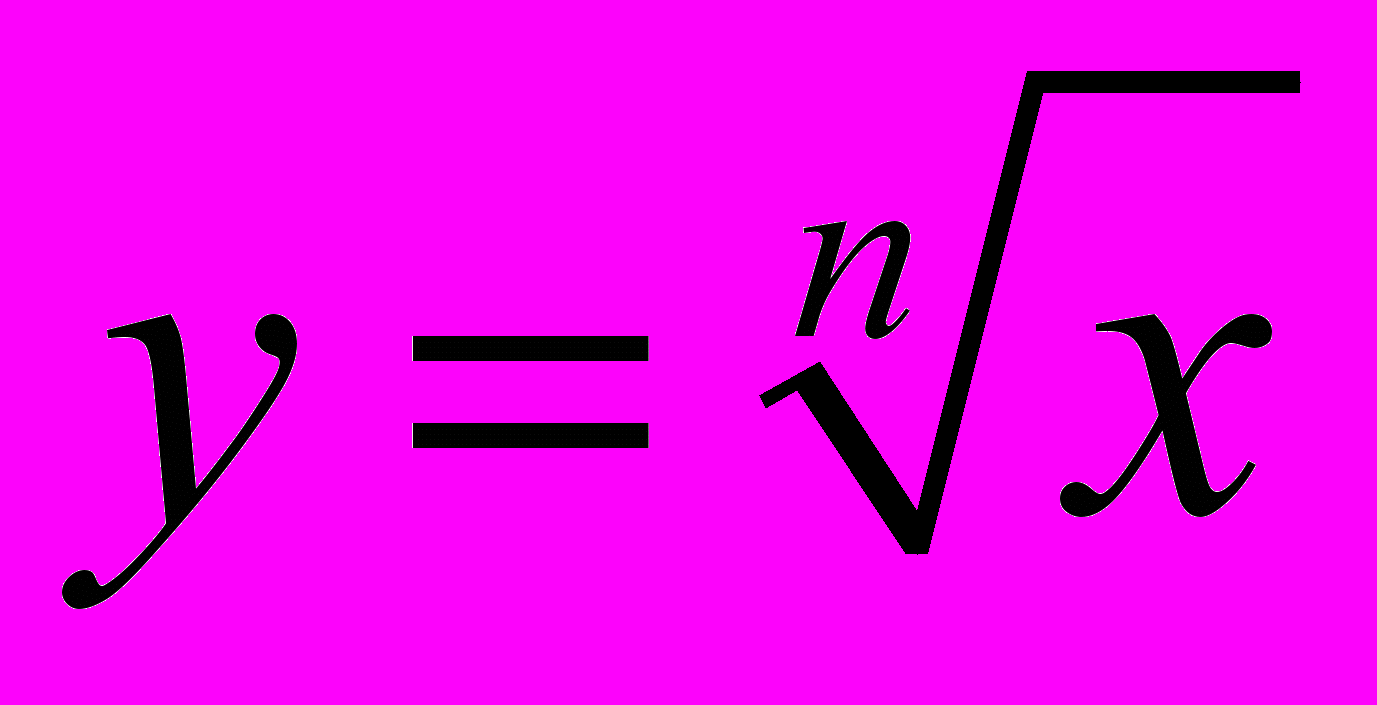и определения свойств функции .

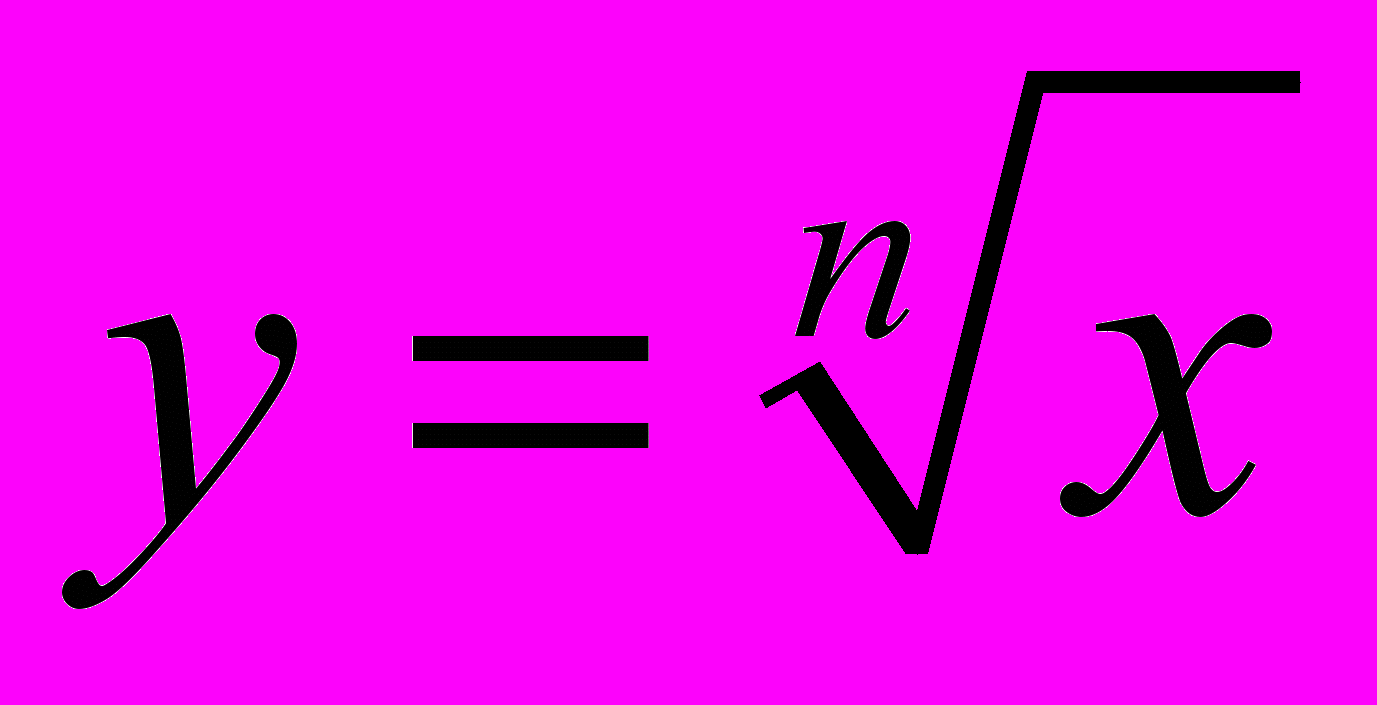Овладение навыками упрощение выражений, содержащих радикал, применяя свойства корня n-й степени.

Обобщить и систематизировать знания учащихся о степенной функции, о свойствах и графиках степенной функции в зависимости от значений оснований и показателей степени.

Показательная и логарифмическая функция (18 ч)

Цели: познакомить учащихся с показа­тельной, логарифмической и степенной функциями; изучение свойств показательной, логарифмической и степенной функций построить в соответствии с принятой общей схемой исследования функций. При этом обзор свойств давать в зависимости от значений параметров. Показательные и логарифмические уравнения и неравенства решать с опорой на изученные свойства функций.

Формирование представлений о показательной и логарифмической функциях, их графиках и свойствах.

Овладение умением понимать и читать свойства и графики логарифмической функции, решать логарифмические уравнения и неравенства.

Овладение умением понимать и читать свойства и графики показательной функции, решать показательные уравнения и неравенства.

Создание условий для развития умения применять функционально-графические представления для описания и анализа закономерностей, существующих в окружающем мире и в смежных предметах.

Первообразная (9ч)

Цели: познакомить учащихся с интег­рированием как операцией, обратной дифференцированию; научить использовать свойства и правила при нахождении первообразных различных функций

Формирование представлений о понятии первообразной.

Овладение умением применения первообразной функции при решении задачи вычисления площадей криволинейных трапеций и других плоских фигур.

Интеграл (10 ч)

Цели: научить учащихся применять первообразную для вычисления площа­дей криволинейных трапеций (формула Ньютона-Лейбница)

Формирование представлений о понятии неопределенного интеграла, определенного интеграла.

Овладение умением применения первообразной функции при решении задачи вычисления площадей криволинейных трапеций и других плоских фигур.

Производная показательной и логарифмической функции(16 ч)

Цели: познакомить учащихся с производной показательной и логарифмической функций, сформировать у учащихся навыки вычисления производной показательной и логарифмической функции, через решение различных типов заданий. Вывод формулы производной показательной функции провести на наглядно-интуитивной основе. При рассмот­рении вопроса о дифференциальном уравнении показатель­ного роста и показательного убывания показательная функ­ция должна выступать как математическая модель, находящая широкое применение при изучении реальных процессов и явлений действительности.

Итоговое повторение(36 ч)

Цели: повторить и обобщить навыки решения основных типов задач по следующим темам: преобразование тригонометрических, степенных, показательных и логарифмических выражений; тригонометрические функции, функция y=, показательная функция, логарифмическая функция; производная; первообразная; различные виды уравнений и неравенств.

Обобщение и систематизация курс алгебры и начала анализа за 11 класса.

Создание условий для плодотворного участия в работе в группе; умения самостоятельно и мотивированно организовывать свою деятельность.

Формирование представлений об идеях и методах математики, о математике, как средстве моделирования явлений и процессов.

Овладение устным и письменным математическим языком, математическим знаниями и умениями.

Развитее логического и математического мышления, интуиции, творческих способностей.

Воспитание понимания значимости математики для общественного прогресса.

Планируемые результаты.

Требования к уровню подготовки учащихся

В результате изучения математики на базовом уровне ученик должен знать и понимать

• значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
  
• значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
  
• универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
  
• вероятностный характер различных процессов окружающего мира;
  

уметь

• находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
  
• проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
  
• строить графики изученных функций;
  
• описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
  
• вычислять в простейших случаях площади с использованием первообразной;
  
• решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;