Кунаревой Арины Вячеславовны по учебному курсу «Алгебра и начала анализа» 10-11 класс Базовый уровень 2009 2010 учебный год рабочая программа
| Вид материала | Рабочая программа |
- Рабочая программа педагога шашаевой татьяны георгиевны, II квалификационная категория, 400.13kb.
- Рабочая программа по алгебре основное общее образование, 7 класс базовый уровень, 544.75kb.
- Штуленко Светланы Николаевны Высшая квалификационная категория по учебному курсу «Экономическая, 219.19kb.
- Приказ №86 от «29.» 08. 2011 г. Рабочая программа педагога зубковой Ирины Александровны,, 449.16kb.
- Сабировой Разины Харисовны, по учебному курсу «География. Начальный курс» 6 класс Базовый, 2245.97kb.
- Список учебников 11 класс 2011-2012 учебный год, 43.9kb.
- Рабочая программа по учебному курсу «Алгебра и начала анализа», 362.1kb.
- Штуленко Светланы Николаевны Высшая квалификационная категория По учебному курсу «Природоведение», 169.8kb.
- Рабочая программа по учебному курсу «География России. Население и хозяйство» в 9 классе, 483.63kb.
- Приказ № от 2009 г. Рабочая программа учителя Жирнова Василия Максимовича по учебному, 238.88kb.
1 2
| «Рассмотрено » Руководитель ШМО _____________Кунарева А.В Протокол № _1_ от «_1__»__09___2009 г. | «Согласовано» Заместитель директора школы по УВР МОУ СОШ №1 _____________ . «_1___»___09___2009 г. | «Утверждено» Директор МОУ СОШ №1 _____________Вовк Е.В. «_1__»____09___2009 г. |
РАБОЧАЯ ПРОГРАММА
Кунаревой Арины Вячеславовны
по учебному курсу
«Алгебра и начала анализа»
10-11 класс
Базовый уровень
2009 - 2010 учебный год
РАБОЧАЯ ПРОГРАММА
ДЛЯ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ
(Базовый уровень)
Пояснительная записка
Статус документа
Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования.
Данная рабочая программа ориентирована на учащихся 10-11 классов и реализуется на основе следующих документов:
1. Программы для общеобразовательных учреждений
Алгебра 7-11 классы составитель Т.А. Бурмистрова. Издательство «Просвещение» 2008 год
2. Сборник нормативных документов «Математика». Составители: Э.Д Днепров, А.Г. Аркадьев. Издательство «Дрофа» Москва 2008.- 128с.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса.
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени среднего (полного) общего образования отводится 5 ч в неделю 10 и 11 классах. Из них на алгебру и начала анализа по 3 часа в неделю или по 102 часа в 10 классе и в 11 классе.
Задачи учебного предмета
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
- систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
- расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
- развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
- знакомство с основными идеями и методами математического анализа.
Цели
Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
- воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ
ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ
АЛГЕБРА
Корни и степени. Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем1. Свойства степени с действительным показателем.
Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е.
Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
Основы тригонометрии. Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования простейших тригонометрических выражений.
Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства.
Арксинус, арккосинус, арктангенс числа.
ФУНКЦИИ
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Обратная функция. Область определения и область значений обратной функции. График обратной функции.
Степенная функция с натуральным показателем, ее свойства и график.
Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
Тригонометрические функции, их свойства и графики; периодичность, основной период.
Показательная функция (экспонента), ее свойства и график.
Логарифмическая функция, ее свойства и график.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат.
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.
Понятие о непрерывности функции.
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции данной функции с линейной.
Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница.
Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных уравнений.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
Календарно-тематическое планирование
Уроков алгебры и начал анализа
(предмет)
Классы:_____10 класс___________________________________________________
Учитель: Кунарева А.В
Кол-во часов за год:
Всего _____102___________________
В неделю ____3 часа_________
Плановых контрольных работ:____8_______, самостоятельных и практических работ: _____21 ________, тестов:___6_ ____
Планирование составлено на основе 1. Программы для общеобразовательных учреждений
Алгебра 7-11 классы составитель Т.А. Бурмистрова. Издательство «Просвещение» 2008 год
2. Сборник нормативных документов «Математика». Составители: Э.Д Днепров, А.Г. Аркадьев. Издательство «Дрофа» Москва 2008.- 128с
Учебник Алгебра и начала анализа. 10-11 классы., Ю.М.Колягин, Ю.В.Сидоров, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин.-М:Мнемозина,2001.
Цели.
Пробудить способность к саморазвитию, самореализации учащихся в процессе обучения,
- Развивать математические, интеллектуальные способности учащихся, логическое мышление, вычислительные навыки, интерес к предмету,
- Воспитывать культуру общения.
Задачи.
Изучить свойства показательной и логарифмическойфункций.
- Научить решать показательные и логарифмические уравнения и неравенства, строить графики функций.
- Приобщать к работе с математической литературой, компьютером
- Предоставить учащимся возможность проанализировать свои способности к математической деятельности.
- Готовить учащихся к сдаче единого государственного экзамена.
| Содержание учебного материала | Кол-во часов | Дата по плану | Дата по факту |
| Глава 1. Действительные числа (13 ч) | | | |
| § 1. Целые и рациональные числа | 1 ч | | |
| § 2-3. Действительные числа. Бесконечно убывающая геометрическая прогрессия | 3 ч | | |
| § 4. Арифметический корень натуральной степени | 2 ч | | |
| § 5-6. Степень с рациональным и действительным показателем. | 5 ч | | |
| Урок обобщения и систематизации знаний | 1 ч | | |
| Контрольная работа №1 | 1 ч | | |
| Глава 3. Показательная функция (9 ч) | | | |
| § 7. Показательная функция, её свойства и график | 3 ч | | |
| § 8.. Показательные уравнения и неравенства | 3 ч | | |
| Уроки обобщения | 2 ч | | |
| Контрольная работа № 2 | 1 ч | | |
| Глава 2. Степенная функция (12 ч) | | | |
| § 9. Степенная функция её свойства и график | 2 ч | | |
| § 10. Взаимно- обратные функции | 1 ч | | |
| § 11.Равносильные уравнения и неравенства | 1 ч | | |
| § 12. Иррациональные уравнения | 3 ч | | |
| § 13. Иррациональные неравенства | 3 ч | | |
| Урок обобщения и систематизации знаний | 1 ч | | |
| Контрольная работа № 3 | 1 ч | | |
| Глава 4. Логарифмическая функция (14 ч) § 14. Логарифмы | 1 ч | | |
| § 15. Свойства логарифмов | 2 ч | | |
| § 16. Десятичные и натуральные логарифмы | 2 ч | | |
| § 17. Логарифмическая функция, её свойства и график | 2 ч | | |
| § 18. Логарифмические уравнения | 2 ч | | |
| § 19. Логарифмические неравенства | 3 ч | | |
| Резерв | 1 ч | | |
| Контрольная работа №4 | 1 ч | | |
| Глава 5. Системы уравнений (13ч) | | | |
| § 20. Способ подстановки | 2 ч | | |
| § 21 Способ сложения | 2 ч | | |
| § 22. Решение систем уравнений различными способами | 4 ч | | |
| § 23. Решение задач с помощью систем уравнений | 3 ч | | |
| Урок обобщения | 1 ч | | |
| Контрольная работа № 5. | 1 ч | | |
| Глава 6. Тригонометрические формулы (21ч) | | | |
| § 24. Радианная мера угла | 1 ч | | |
| § 25. Поворот точки вокруг начала координат | 2 ч | | |
| § 26. Определение синуса, косинуса и тангенса угла | 2 ч | | |
| § 27. Знаки синуса, косинуса и тангенса | 1 ч | | |
| § 28. Зависимость между синусом, косинусом и тангенсом одного и того же угла | 1 ч | | |
| § 29. Тригонометрические тождества | 2 ч | | |
| § 30. Синус, косинус и тангенс углов α и -α | 1 ч | | |
| § 31. Формулы сложения | 2 ч | | |
| § 32. Синус, косинус и тангенс двойного угла | 2 ч | | |
| § 33.Синус, косинус, и тангенс половинного угла | 1 ч | | |
| § 34. Формулы приведения | 1 ч | | |
| § 35. Сумма и разность синусов, косинусов | 2 ч | | |
| § 36. Произведение синусов и косинусов | 1 ч | | |
| Урок обобщения | 1 ч. | | |
| Контрольная работа № 6. | 1 ч | | |
| Глава 6. Тригонометрические уравнения (17ч) | | | |
| § 37. Уравнение Соs х =а | 2 ч | | |
| § 38. Уравнение Sin х =а | 2 ч | | |
| § 39. Уравнение tg х = а | 2 ч | | |
| § 40. Уравнение сtg х = а | 2 ч | | |
| § 41. Уравнения, сводящиеся к квадратным | 2 ч | | |
| § 42. Уравнение, однородные относительно Sin х и Соs х | 1 ч | | |
| § 43. Уравнение, линейное относительно Sin х и Соs х § 44. Решение уравнений методом замены неизвестного | 1 ч | | |
| | | ||
| § 45. Решение уравнений методом разложения на множители | 1 ч | | |
| § 46. Различные приёмы решения тригонометрических уравнений § 48. Уравнения, содержащие корни и модули | 1 ч | | |
| | | ||
| § 49. Системы тригонометрических уравнений | 1 ч | | |
| Урок обобщения 1 ч. | |||
| Контрольная работа № 6 | 1 ч | | |
| Повторение | 3 ч | | |
Календарно-тематическое планирование
Уроков алгебры и начал анализа
(предмет)
Классы:_____11 класс___________________________________________________
Учитель: Кунарева А.В.
Кол-во часов за год:
Всего _____102___________________
В неделю ____3 часа_________
Плановых контрольных работ:____5_______, самостоятельных и практических работ: _____16 ________, тестов:___16_ ____
Планирование составлено на 1. Программы для общеобразовательных учреждений
Алгебра 7-11 классы составитель Т.А. Бурмистрова. Издательство «Просвещение» 2008 год
2. Сборник нормативных документов «Математика». Составители: Э.Д Днепров, А.Г. Аркадьев. Издательство «Дрофа» Москва 2008.- 128с
Учебник__ Алгебра и начала анализа: учеб. для 10-11 кл. ., Ю.М.Колягин, Ю.В.Сидоров, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин.-М:Мнемозина,2001.
| П/п | Дата | Количество часов | Тема | Требования стандарта | |
| Теоретических | Практических | Знать Уметь | |||
| | | 5 | 8 | Глава 8. « Тригонометрические функции» (13ч.) | |
| 1 | | 0,5 | 0,5 | Область определения и множество значений тригонометрических функций. | Функции, Область определения и множество зачений. |
| 2-3 | | 1 | 1 | Четность, нечетность, периодичность тригонометрических функций. | Свойства функции: периодичность. |
| 4-6 | | 1 | 2 | Свойства функции y=cos x и график. | Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функции: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания функции, наибольшее и наименьшее значения. Графическая интерпретация. Применение функциональных зависимостей в реальных процессах и явлениях. Преобразование графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат и симметрия относительно прямой у=х, растяжение и сжатие вдоль координатных осей. |
| 7-8 | | 1 | 1 | Свойсва функции у=sinx и ее график. Проверочная работа №1. С/р №1. | |
| 9-10 | | 1 | 1 | Свойства и графики функций y=tg x и y=ctg x. С/р №2. | |
| 11 | | 0,5 | 0,5 | Обратные тригонометрические функции. | Обратная функция. Область определения и область значений обратной тригонометрической функции. График обратной функции. |
| 12 | | | 1 | Урок обобщения. | |
| 13 | | | 1 | Контрольная работа №1. | |
| | | 10,5 | 15,5 | Глава 1. Производная и ее применения (26 ч.). | |
| 14-15 | | 1 | 1 | Предел функции. Непрерывные функции. | Понятие о непрерывности функции. |
| 16-17 | | 1 | 1 | Производная. | Понятие о производной функции, физический и геометрический смысл производной. |
| 18-20 | | 1 | 2 | Правила дифференцирования. С/р №3. | Производные суммы, разности, произведения и частного. |
| 21-22 | | 1 | 1 | Производная степенной функции. Т/р №2. | Производная степенной функции. |
| 23-25 | | 1 | 2 | Производные некоторых элементарных функций. С/р №4. | Производные основных элементарных функций. |
| 26-27 | | 1 | 1 | Геометрический смысл производной. Т/р №3. | Уравнение касательной к графику функции |
| 28-29 | | 1 | 1 | Возрастание и убывание функции. С/р№5. | Промежутки возрастания и убывания функции, наибольшее и наименьшее значение функции |
| 30-31 | | 1 | 1 | Экстремумы функции. | Значения функции, точки экстремума (локального максимума и минимума). |
| 32-34 | | 1 | 2 | Применение производной к построению графиков функции. С/р №6. | Применение производной к исследованию функций и построению графиков. |
| 35-36 | | 1 | 1 | Наибольшее и наименьшее значение функции. Т/р №4. | Наибольшее и наименьшее Значения функции, точки экстремума (локального максимума и минимума). |
| 37 | | 0,5 | 0,5 | Производная второго порядка, выпуклость и точки перегиба. | Вторая производная и ее физический смысл. |
| 38 | | | 1 | Урок обобщения. | |
| 39 | | | 1 | Контрольная работа № 2. | |
| | | 3,5 | 8,5 | Интеграл (12 ч.). | |
| 40-41 | | 1 | 1 | Первообразная. | Первообразная. |
| 42-43 | | 0,5 | 1,5 | Правила нахождения первообразных. | |
| 44-46 | | 1 | 2 | Площадь криволинейной трапеции. Интеграл и его вычисление. С/р №7. | Понятие об определенном интеграле как площади криволинейной трапеции. Формула Ньютона- Лейбница. |
| 47-48 | | | 2 | Вычисления площадей с помощью интегралов. | |
| 49 | | 1 | | Применение интегралов при решении физических задач. | Примеры применения интеграла в физике и геометрии. |
| Простейшие дифференциальные уравнения. | | ||||
| 50 | | | 1 | Урок обобщения. | |
| 51 | | | 1 | Контрольная работа №3. | |
| | | 5 | 7 | Комплексные числа (12ч.). | |
| 52 | | 0,5 | 0,5 | Определение комплексных чисел. | |
| 53 | | 0,5 | 0,5 | Сложение и умножение комплексных чисел. | |
| 54 | | 0,5 | 0,5 | Модуль комплексного числа. | |
| 55 | | 0,5 | 0,5 | Вычитание и деление комплексных чисел. С/р №8. | |
| 56-57 | | 1 | 1 | Геометрическая интерпретация комплексного числа. | |
| 58 | | 0,5 | 0,5 | Тригонометрическая форма комплексного числа. | |
| 59-60 | | 1 | 1 | Свойства модуля и аргумента комплексного числа. | |
| 61 | | 0,5 | 0,5 | Квадратное уравнение с комплексным неизвестным. С/р №9. | |
| | | | | Примеры решения алгебраических уравнений. | |
| 62 | | | 1 | Урок обобщения. | |
| 63 | | | 1 | Контрольная работа №4. | |
| | | 4,5 | 6,5 | Элементы комбинаторики (11 ч.). | |
| 64-65 | | 1 | 1 | Комбинаторные задачи. Правило умножения. | Решение комбинаторных задач. |
| 66 | | 0,5 | 0,5 | Перестановки. | |
| 67-68 | | 1 | 1 | Размещения. | |
| 69-70 | | 1 | 1 | Сочетания и их свойства. | |
| 71-72 | | 1 | 1 | Биномиальная формула Ньютона. С/р №10. | Биномиальная формула Ньютона. Свойства биноминальных коэффициентов. |
| 73 | | | 1 | Урок обобщения. | |
| 74 | | | 1 | Контрольная работа № 5. | |
| | | 3,5 | 6,5 | Знакомство с вероятностью (10ч.). | |
| 75 | | 0,5 | 0,5 | Вероятность события. | |
| 76 | | 0,5 | 0,5 | Сложение вероятностей. | |
| 77 | | 0,5 | 0,5 | Вероятность противоположного события. С/р №11. | |
| 78-79 | | 1 | 1 | Условная вероятность. | |
| 80-82 | | 1 | 2 | Вероятность произведения независимых событий. С/р №12. | |
| 83 | | | 1 | Урок обобщения. | |
| 84 | | | 1 | Контрольная работа №6. | |
| 85-102 | | | 18 | Повторение (18ч.). Т/р №5-10. С/р №13-16. | |
ОСНОВНОЕ СОДЕРЖАНИЕ
(204часа)
АЛГЕБРА
Корни и степени. Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е.
Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
Основы тригонометрии. Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования простейших тригонометрических выражений.
Простейшие тригонометрические уравнения и неравенства. Арксинус, арккосинус, арктангенс числа.
ФУНКЦИИ
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Обратная функция. Область определения и область значений обратной функции. График обратной функции.
Степенная функция с натуральным показателем, её свойства и график.
Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
Тригонометрические функции, их свойства и графики; периодичность, основной период.
Показательная функция (экспонента), её свойства и график.
Логарифмическая функция, её свойства и график.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой
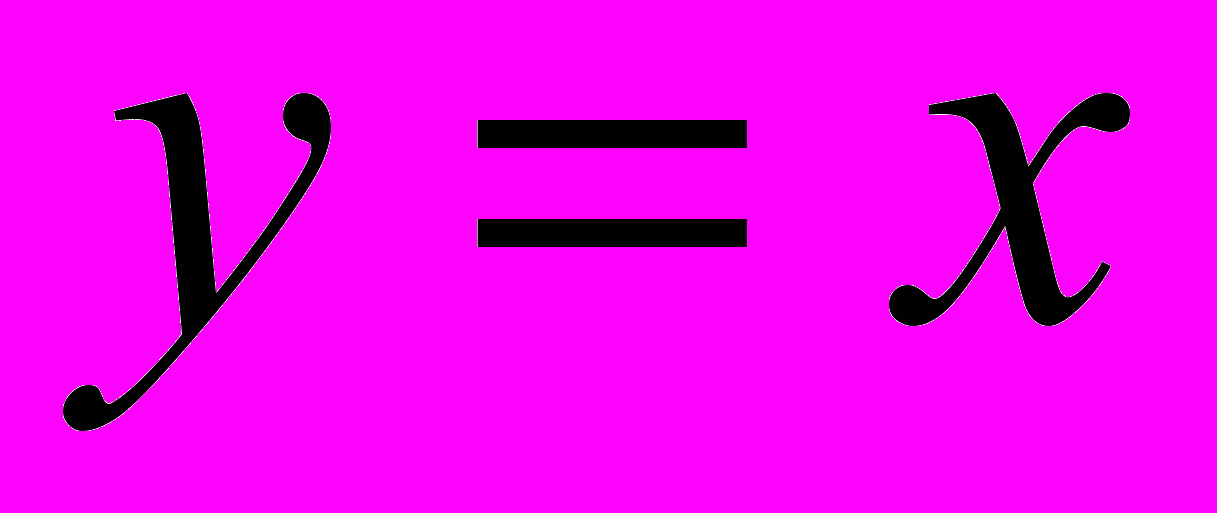, растяжение и сжатие вдоль осей координат. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.
Понятие о непрерывности функции.
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции данной функции с линейной.
Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница.
Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных и тригонометрических уравнений.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
| Темы учебного курса 10 класса |
|
| Темы учебного курса 11 класса |
|
Первообразная
Цели: познакомить учащихся с интегрированием как операцией, обратной дифференцированию; научить использовать свойства и правила при нахождении первообразных различных функций
Формирование представлений о понятии первообразной.
Овладение умением применения первообразной функции при решении задачи вычисления площадей криволинейных трапеций и других плоских фигур.
Интеграл
Цели: научить учащихся применять первообразную для вычисления площадей криволинейных трапеций (формула Ньютона-Лейбница)
Формирование представлений о понятии неопределенного интеграла, определенного интеграла.
Овладение умением применения первообразной функции при решении задачи вычисления площадей криволинейных трапеций и других плоских фигур.
Обобщение понятия степени
Цели: познакомить учащихся с понятия корня n-й степени и степени с рациональным показателем, которые являются обобщением понятий квадратного корня и степени с целым показателем. Следует обратить внимание учащихся на то, что рассматриваемые здесь свойства корней и степеней с рациональным показателем аналогичны тем свойствам, которыми обладают изученные ранее квадратные корни и степени с целыми показателями. Необходимо уделить достаточно времени отработке свойств степеней и формированию навыков тождественных преобразований.
Формирование представлений корня n-ой степени из действительного числа, функции
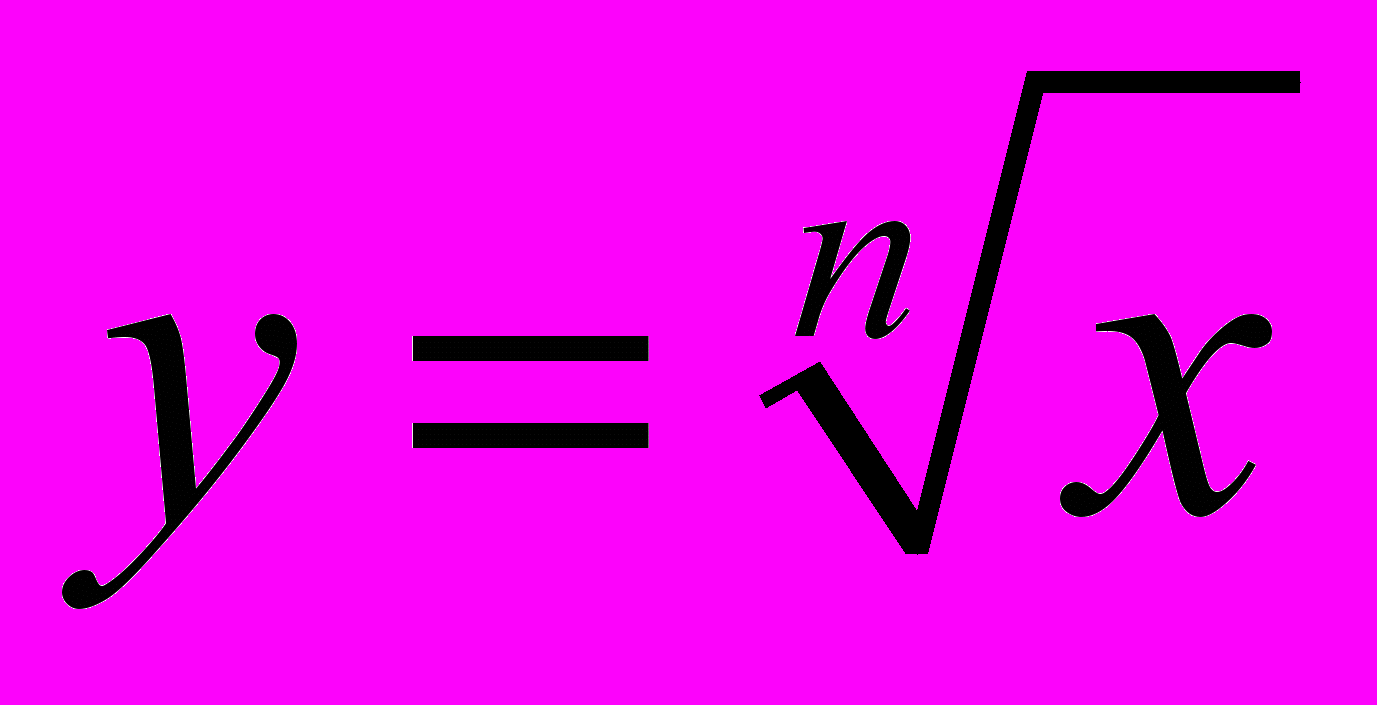и графика этой функции.Овладение умением извлечения корня, построения графика функции
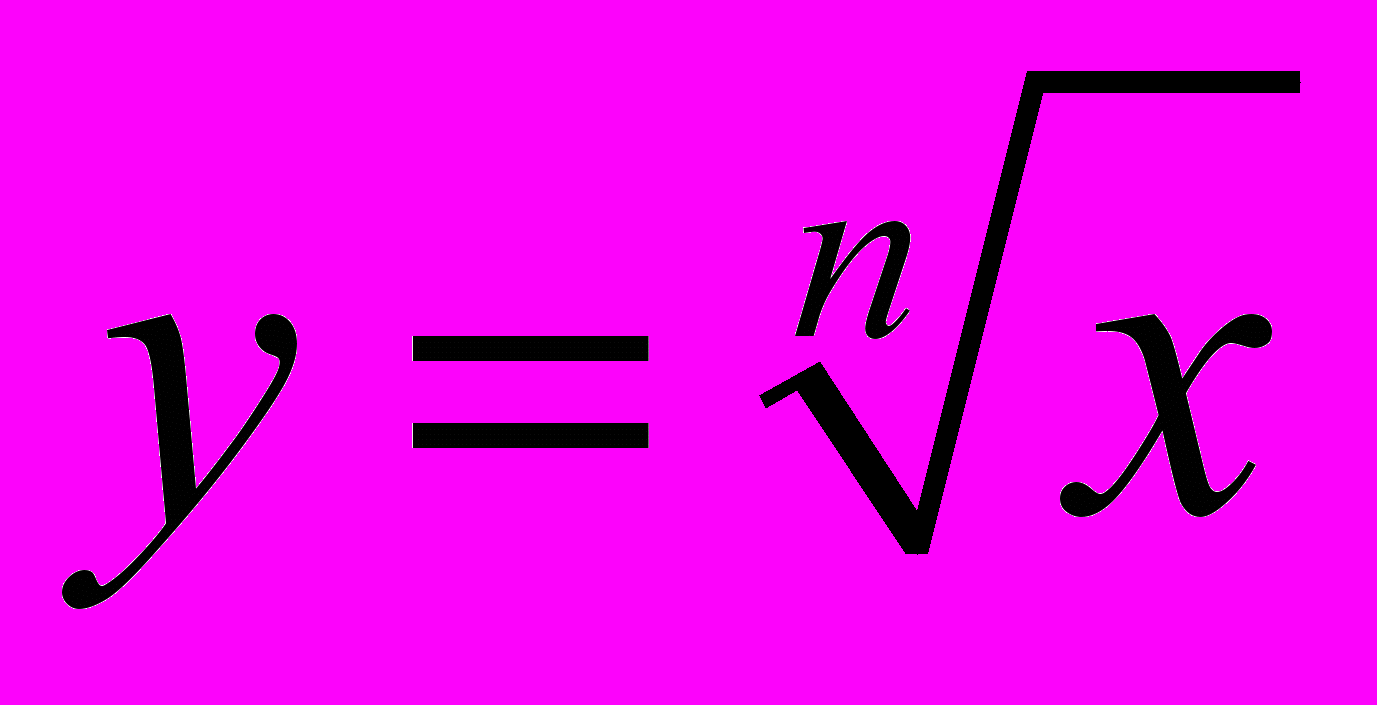и определения свойств функции 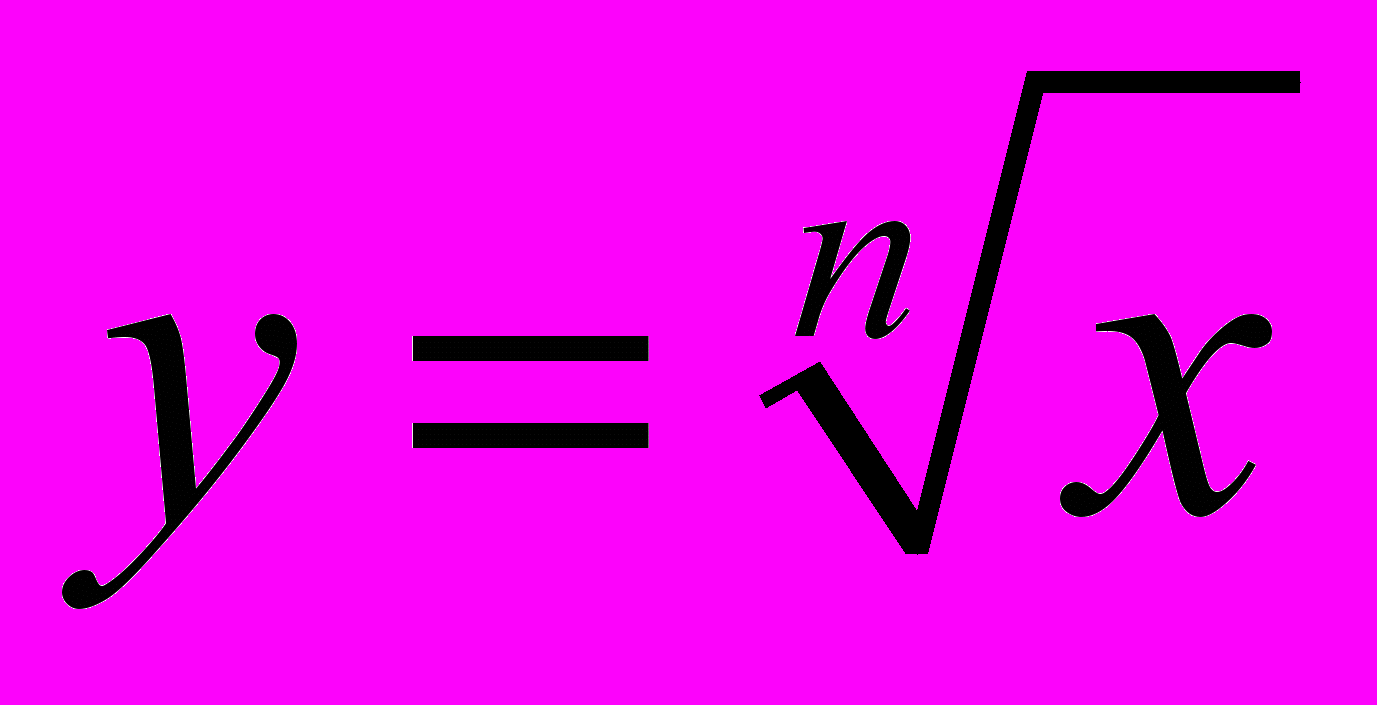. Овладение навыками упрощение выражений, содержащих радикал, применяя свойства корня n-й степени.
Обобщить и систематизировать знания учащихся о степенной функции, о свойствах и графиках степенной функции в зависимости от значений оснований и показателей степени.
Показательная и логарифмическая функция
Цели: познакомить учащихся с показательной, логарифмической и степенной функциями; изучение свойств показательной, логарифмической и степенной функций построить в соответствии с принятой общей схемой исследования функций. При этом обзор свойств давать в зависимости от значений параметров. Показательные и логарифмические уравнения и неравенства решать с опорой на изученные свойства функций.
Формирование представлений о показательной и логарифмической функциях, их графиках и свойствах.
Овладение умением понимать и читать свойства и графики логарифмической функции, решать логарифмические уравнения и неравенства.
Овладение умением понимать и читать свойства и графики показательной функции, решать показательные уравнения и неравенства.
Создание условий для развития умения применять функционально-графические представления для описания и анализа закономерностей, существующих в окружающем мире и в смежных предметах.
Производная показательной и логарифмической функции
Цели: познакомить учащихся с производной показательной и логарифмической функций, сформировать у учащихся навыки вычисления производной показательной и логарифмической функции, через решение различных типов заданий. Вывод формулы производной показательной функции провести на наглядно-интуитивной основе. При рассмотрении вопроса о дифференциальном уравнении показательного роста и показательного убывания показательная функция должна выступать как математическая модель, находящая широкое применение при изучении реальных процессов и явлений действительности.
Итоговое повторение
Цели: повторить и обобщить навыки решения основных типов задач по следующим темам: преобразование тригонометрических, степенных, показательных и логарифмических выражений; тригонометрические функции, функция y=
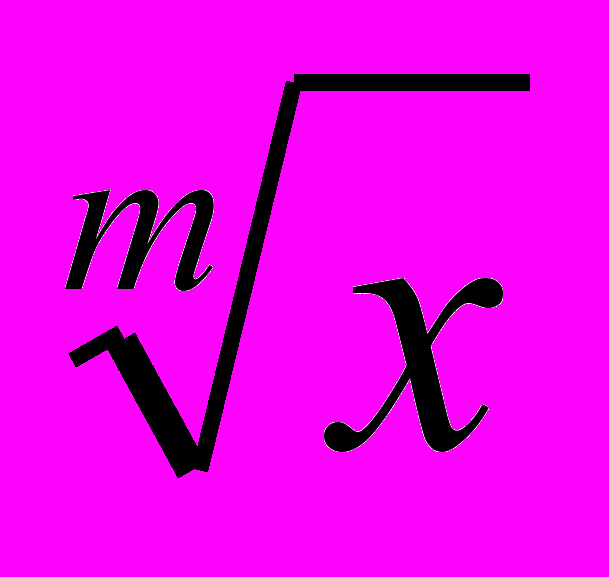, показательная функция, логарифмическая функция; производная; первообразная; различные виды уравнений и неравенств.Обобщение и систематизация курс алгебры и начала анализа за 11 класса.
Создание условий для плодотворного участия в работе в группе; умения самостоятельно и мотивированно организовывать свою деятельность.
Формирование представлений об идеях и методах математики, о математике, как средстве моделирования явлений и процессов.
Овладение устным и письменным математическим языком, математическим знаниями и умениями.
Развитее логического и математического мышления, интуиции, творческих способностей.
Воспитание понимания значимости математики для общественного прогресса.