К. Д. Ушинский Условия возникновения опыта моу «Репяховская средняя общеобразовательная школа»
| Вид материала | Документы |
СодержаниеПункт «Силён? Реши!» Пункт «Устал? Отдохни!» Командировочное удостоверение 1 аршин = 16 вершкам = 71 см Ход урока Количество учащихся данного уровня |
- Приказ №165 от «7» декабря 2011 г. «Об итогах районного конкурса сочинений «И отблеск, 24.24kb.
- Приказ №163 от «7» декабря 2011 г. «Об итогах районного конкурса мозаичных картин «Любо, 15.63kb.
- Порядок и условия оплаты труда работников моу «Трудармейская средняя общеобразовательная, 328.3kb.
- И. Э. Торкунова директор моу «Школа №8» моу «Средняя общеобразовательная школа №8», 1447.31kb.
- Моу «Тишанская средняя общеобразовательная школа Волоконовского района Белгородской, 216.48kb.
- План работы моу «Репяховская основная общеобразовательная школа» на зимних каникулах, 161.25kb.
- Публичный доклад директора моу «Средняя общеобразовательная школа №16» г. Серпухова, 616.15kb.
- Доклад моу «Средняя общеобразовательная школа №39», 659.53kb.
- Моу «Саскылахская средняя общеобразовательная школа» Анабарский национальный(долгано-эвенкийский)улус, 362kb.
- Доклад моу «Средняя общеобразовательная школа №24 п. Бира», 1155.85kb.
Пункт «Силён? Реши!»
№ 1. Задача. Первое число больше второго на 4. Разность между квадратом первого числа и вторым числом равна 46. Найдите эти числа.
Решение. Пусть х – первое число. Тогда второе число равно (х – 4).
х2 – (х – 4) = 46; х2 – х – 42 = 0; х1 = 7; х2 = – 6. Ответ: 7 и 6.
№ 2. Решить уравнение: 4 х2 + х 5 х – 1 х2 + 17


 – = .
– = .3 6 9
Решение. 6 (4 х2 + х) – 3 (5 х – 1) = 2 (х2 + 17); 24 х2 + 6 х – 15 х + 3 = 2 х2 + 34; 22 х2 – 9 х – 31 = 0; D = 81 + 22 * 4 * 31 = 81 + 2728 = 2809; х1 = (9 + 53) / 44 = 1 9/22; х2 = (9 – 53) / 44 = –1. Ответ: –1; 1 9/22.
Пункт «Устал? Отдохни!»
Ребята разгадывают кроссворды.
Итог урока
а) Ребята сдают свои командировочные удостоверения для росписи учителя.
б) Заключительное слово учителя. Вот и закончилась ваша командировка. От всей души благодарю вас за выполненную работу. Хочется особо отметить следующих учащихся: …
Командировочное удостоверение
Выдано учени___ 8 класса _____________________ ____________________.
| № п/п | Пункт назначения | Оценка работы | Рекомендации |
| 1 | Пункт № 4 | | |
| 2 | Пункт № 1 | | |
| 3 | Пункт № 2 | | |
| 4 | Пункт № 3 | | |
| 5 | «Силён? Реши!» | | |
| 6 | «Устал? Отдохни!» | | |
Время возвращения: ___ ч ___ мин.
Выводы: _____________________________________________________________________
Приложение 5
Внеклассное занятие.




Биография
Софья Васильевна Ковалевская
«Я чувствую, что предназначено служить истине – науке и прокладывать новый путь женщинам, потому что это значит служить справедливости. Я очень рада, что родилась женщиной, так как это даёт мне возможность одновременно служить истине и справедливости».
(С.В. Ковалевская.)
Родилась Софья Васильевна в Москве 15 января 1850 года. Её отец – крупнопоместный дворянин, артиллерийский генерал. Её род идёт от польского витязя Круковского и дочери венгерского короля – рыцаря Матея, мецената и библиофила. Выйдя в отставку, генерал переехал с семьёй из Москвы в своё имение Палибино, недалеко от границы с Литвой. Софье тогда было около 6 лет. Жизнерадостная девочка с круглым и необыкновенно выразительным лицом, с ямочкой на подбородке и глазами, то блестящими и искрящимися, то глубоко мечтательными, училась усердно, настойчиво и самостоятельно осмысливала всё, что изучала. Рано пристрастившись к чтению, сначала она увлекалась поэзией. И в свои 12 лет она твёрдо решила стать поэтессой.
Тем временем с возрастающей силой и скоростью стало у Софьи проявляться математическое дарование. … Однажды отец спросил у своей дочери, любит ли она арифметику
- Нет, папа,- чисто сердечно призналась девочка.
Но искра интереса быстро разгорелась, и через 4 месяца на этот же вопрос она ответила: «Да, папочка, я люблю заниматься арифметикой, она доставляет мне удовольствие»…
Проходя раздел об отношении длины окружности к длине диаметра, Софья пришла к выводу самостоятельно и своеобразным путём. «Многие, которым никогда не представлялось случая узнать более математику, смешивают её с арифметикой и считают её наукой сухой. В сущности же это наука, требующая большой фантазии, и один из первых математиков нашего столетия говорит совершенно верно, что нельзя быть математиком, не будучи в тоже время и поэтом в душе». Это были слова С.В Ковалевской.

В старину в России применялись другие меры массы, чем в настоящее время. Так для взвешивания мелких, но дорогих товаров, применялся золотник (около 4 граммов). В торговле использовались фунт (один фунт равен 96 золотникам), пуд (1 пуд равен 40 фунтам), берковец (1 берковец равен 10 пудам).
Но наиболее древняя русская мера массы – «гривна», или «гривенка» (около 410 граммов), а появилась она раньше золотников, фунтов и пудов.
С развитием торговли назрела необходимость введения единой системы мер, удобной для всех стран, с простыми соотношениями между единицами. И такая система называется метрической системой мер. Она принята большинством стран. А в России существует с 1899 года.
Вопросы
для игры
«Счастливый случай».
- Найдите 1% метра.
- Какое число записывалось в Древнем Риме буквой Д?
- Чему равен 1 пуд?
- Назовите формулу периметра прямоугольника со сторонами а и в.
- Специфическая единица измерения объёма нефти.
- Назовите наименьшее натуральное число.
- Число, обращающее уравнение в верное равенство.
- Чему равна сумма углов квадрата?
- Отрезок, соединяющий точку окружности с центром.
- Масса 1 м3 воды.
- Может ли при делении получиться 0?
- Чему равна ¼ часть часа?
- Какую часть часа составляют 20 минут?
- Площадь квадрата 49 см2. Чему равен его периметр?
- Периметр прямоугольника равен 64 см.Чему равна сторона квадрата с тем же периметром?
- Что больше: 1,8 х 5 или 5,1 х 2?
- К натуральному числу справа приписали три 0. Во сколько раз увеличилось число?
- Назовите инструмент для построения окружности.
КРОССВОРД
Положительные и отрицательные
числа.
По горизонтали: По вертикали:
- Тысячная часть числа. 6. Число, которому соответствует
- Числа, в которые входят данная точка на числовой прямой.
целые числа, отрицательные и 7. Равенство двух отношений.
положительные, дробные. 8. Непересекающиеся прямые на
- Два числа, отличающиеся плоскости.
друг от друга только знаками. 9. Сумма противоположных
- Числа со знаком «минус». чисел.
- Два числа, произведение
которых равно единице.






Измерение играет огромную роль в науке. Д.И. Менделеев говорил, что наука начинается с тех пор, как начинают измерять, и что точная наука не мыслима без меры.
Древнейшие единицы измерения были связаны с частями человеческого тела, ибо они – то всегда при человеке. Так, в качестве единиц длины в древней Руси использовались такие меры:
локоть (45 см)-расстояние от конца пальцев до локтя;
ладонь (10 см) – ширина кисти руки;
коса сажень (248 см) – расстояние от пальцев левой ноги до конца пальцев поднятой правой руки;
маховая сажень (176 см) – расстояние между концами пальцев расставленных в стороны рук;
«ступня»-фут (31 см); «большой палец» - дюйм (25 мм);
ярд (91 см) – расстояние от носа до конца среднего пальца вытянутой руки;
«поприще»- верста (500 сажень, 1067 м)
1 сажень = 3 аршина = 7 футов = 213 см
1 аршин = 16 вершкам = 71 см
1 вершок = 44 мм
1 фут = 12 дюймов =304 см
миля = 1852 м
кабельтовый = 185 м
1.Дайте определение понятию «процент».
2. Найдите 1 % от 100 рублей.
3. Число разрядов в классе.
4. Какой буквой записывалось число 50 в Древнем Риме?
5. Формула площади прямоугольника со сторонами а и в.
6. Единица измерения скорости на море.
7. Как найти неизвестное делимое?
8. Третья буква древнегреческого алфавита.
9. Может ли при умножении получиться 0.
10. Место, занимаемое цифрой в записи числа.
11. Единица массы драгоценных камней.
12. Объём 1 кг воды.
13. Чему равно 13 х 25 х 0 х 0,1 ?
14. Что легче: 1 кг ваты или 1 кг железа?
15. Как найти неизвестное уменьшаемое?
16. Прибор для измерения углов.
17. Площадь прямоугольника 36 см2. Чему равна сторона квадрата с такой же площадью?
18. Что больше: 34 х 54 или 43 х 55 ?
19. Бежала тройка лошадей. Каждая лошадь пробежала 5 км. Сколько км проехал ямщик?
20. К однозначному числу больше 0 приписали такую же цифру. Во сколько раз увеличилось число ?
21. Уменьшаемое на 375 больше вычитаемого. Чему равна их разность?
22. Какое число больше: наименьшее четырёхзначное или наибольшее трёхзначное?

По горизонтали: По вертикали:
1.Какая дробь меньше единицы? 2.Периметр прямоугольника
2.Площадь квадрата со стороной 3. со стороной 6см и 4 см.
3.Значение переменной при 6. Угол, на который
решении уравнения. поворачивается солдат по команде.
4.Какую часть периметра 7. Инструмент для измерения углов.
равностороннего треугольника 8. Какую долю составляют сутки от
составляет длине одной стороны. недели?
5.Автор первого учебника 9. Какую часть периметра квадрата
по математике. составляет длина одной стороны?

Более двадцати веков и с каждым последующим веком всё чаще творческое напряжение человеческой мысли завершается удовлетворённо – эмоциональным восклицанием «Эврика!» По преданию это ставшие крылатым восклицанием, знаменующее торжество разума, подарил человечеству великий Архимед – самый знаменитый в плеяде самобытных математиков Древней Греции, обладавшей, по словам английского математика Джона Валлиса, поразительной проницательностью: «Он заложил первоосновы почти всех открытий, развитием которых гордится наш век». По сей день во всех школах мира изучается закон Архимеда о телах, погруженных в жидкость.
Родина Архимеда – г. Сиракузы (Сицилия). Первоначальным его образованием руководил отец – математик и астроном Фидий. Позже попав в Александрию (Египет), были достигнуты в теоретической механике и её практических применениях блестящие успехи. Замечательным его изобретением была машина для поливки полей, также он делает выдающиеся открытия в геометрии, конструирует разнообразные остроумные оборонительные сооружения и военные машины для своего города.
Изумительное изобретение Архимеда – механический небесный глобус – своеобразный планетарий, демонстрировавший все видимые движения небесных тел.
В день взятия Сарак уз римским легионами Архимед сидел около своего дома и чертил на земле фигуры. Когда к нему подбежал воин он просил: « Не трогай моих чертежей!».
Открытия Архимеда имеют очень важную роль в развитии науки.
Приложение 6
Класс: 9
Тема: «РЕШЕНИЕ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНЫМ»
Тип урока: занятие по изучению нового материала и первичное закрепление
умений и навыков учащихся.
Цели:
- обеспечить закрепление материала, изученного на предыдущем уроке;
- организовать деятельность учащихся по усвоению алгоритма решения уравнений, приводимых к квадратным;
- создать условия для формирования и первичного закрепления умений решать уравнения, приводимые к квадратным;
- содействовать формированию исследовательской культуры, развивать культуру самоороганизации.
Оборудование:
- сборники под редакцией Кузнецовой;
- тесты для проведения мини-экзамена;
- вопросы для блицтурнира;
- карточки для устного счёта.
Эпиграф: «Главный труд в школе – это учение. А чтобы оно принесло успех, надо работать рационально и самостоятельно».
Ход урока
- Организационный этап.
а) Настрой учащихся на начало урока.
б) Проверка готовности к уроку.
в) Вводное слово учителя.
Скажите, ребята, чем мы занимались на последнем уроке алгебры?
Какие уравнения называются целыми?
Все ли целые уравнения можно решить? Почему?
Какие способы решения целых уравнений вам известны?
Итак, сегодня мы продолжим решать целые уравнения. Тема урока: « Решение уравнений, приводимых к квадратным».
На уроке вы, ребята, должны показать знания, умения и навыки решения целых уравнений и пополнить свой багаж знаний новыми методами решения целых уравнений, изучив алгоритм решения уравнений, приводимых к квадратным.
Своеобразным эпиграфом к нашему уроку я взяла слова, которые мне очень нравятся, и, думаю, предназначены, прежде всего, вам: «Главный труд в школе – это учение. А чтобы оно принесло успех, надо работать рационально и самостоятельно». Я желаю вам успеха.
- Проверка домашнего задания (5 минут).
а) Просмотр тетрадей.
б) Консультация учителя (по необходимости).
в) Работа у доски (2 человека) + блиц-опрос.
№ 1. Решить уравнение (сборник Кузнецовой, стр. 102).
- (1). х3 + 3 х2 – 2 х – 6 = 0, 2.5 (1). 3 х2 (2 х – 1) + х (2 х – 1) +2 (1 – 2 х) = 0,
х2 (х – 3) – 2 (х – 3), (2 х – 1) (3 х2 + х – 2) = 0,
(х + 3) (х2 – 2) = 0, х1 = 0,5, 3 х2 + х – 2 = 0,
х1 = 0, х2 = ±
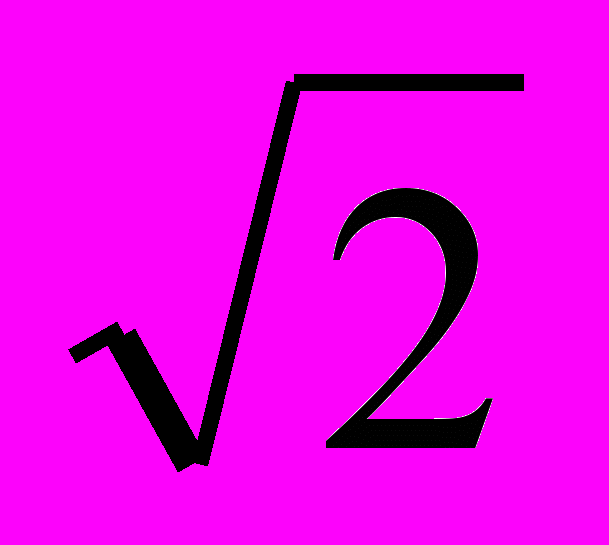 . D = 25, х = (– 1 ± 5) / 6,
. D = 25, х = (– 1 ± 5) / 6,Ответ: 0; ±
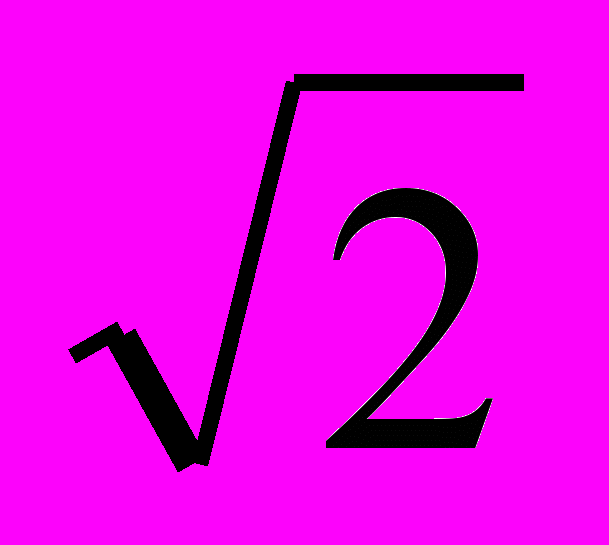 . х2 = – 1, х3 = 2/3.
. х2 = – 1, х3 = 2/3.Ответ: 0,5; –1; 2/3.
Блиц-опрос (повторение материала, устная работа, 4 минуты).
Решить уравнения:
- х2 – 11 х + 28 = 0. (Ответ: 7; 4.)
- х2 + 9 х + 20 = 0. (Ответ: –5; –4.)
- х2 – 13 х + 12 = 0. (Ответ: 12; 1.)
- х2 – 8 х – 20 = 0. (Ответ: 10; –2.)
- х2 – 15 х + 50 = 0. (Ответ: 10; 5.)
- Мини-экзамен (в виде новой формы сдачи экзамена по карточкам, указаны нормы оценок, 15 минут).
Решить уравнения:
а) (х – 7) (х + 8) = 0.
А. 5; 6. Б. – 7; - 8. В. 7; - 8. Г. 0; 1.
б) х3 – х5 = 0.
А. 0; 1. Б. 0; – 1; 1. В. нет корней. Г. – 1; 1.
в) (5 – х) (5 + х) – х (х + 6) = 17.
А. 2; 3. Б. 4; 1. В. –4; 1. Г. – 1; 4.
На 5 баллов (а, в, в + г, д).
г) х3 – 4 х2 – 9 х + 36 = 0,
х2 (х – 4) – 9 х (х – 4) = 0,
(х – 4) (х2 – 9) = 0. Ответ: – 3; 3; 4.
д) 2 х2 (2 х – 5) + х (2 х – 5) + (5 – 2 х) = 0,
(2 х – 5) (2 х2 + х – 1) = 0. Ответ: – 1; 0,5; 2,5.
е) (х2 + 6 х)2 – 5 (х2 + 6 х) = 24 (проблема!),
t2 – 5 t – 24 = 0,
t1 = 8, t2 = – 3,
х2 + 6 х = 8 или х2 + 6 х = – 3,
х2 + 6 х – 8 = 0, х2 + 6 х + 3 = 0,
D = 36 + 32 = 68; D = 36 – 12 = 24,
х = (– 6 ± 2
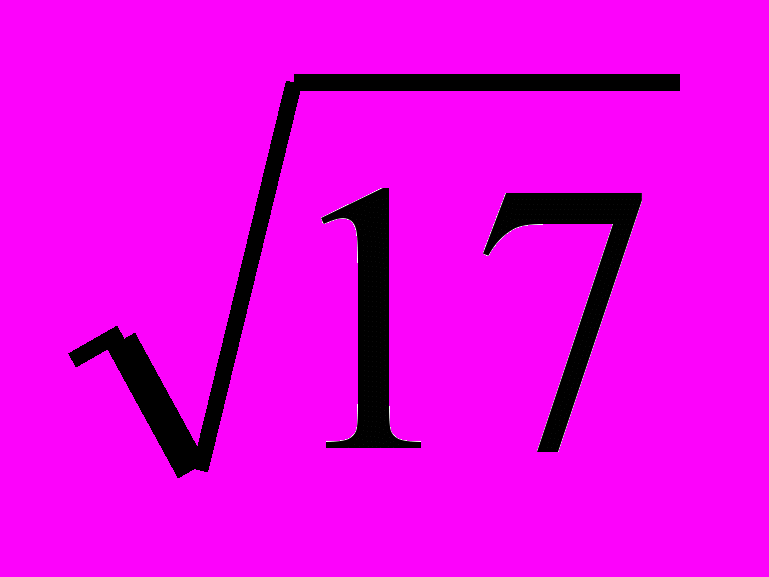 ) / 2, х = (– 6 ± 2
) / 2, х = (– 6 ± 2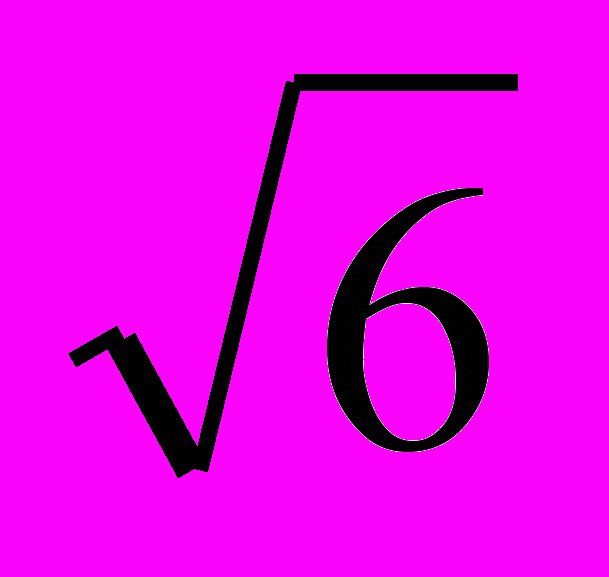 ) / 2,
) / 2,х = –3 ±
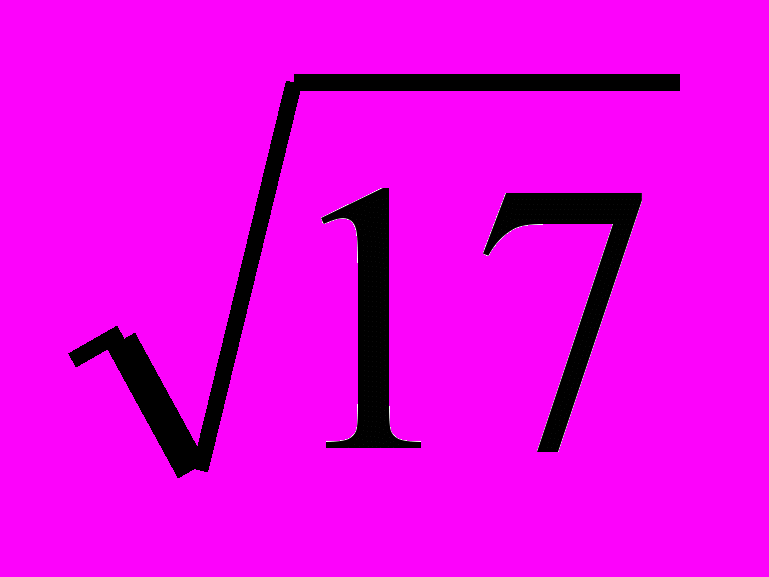 , х = –3 ±
, х = –3 ± 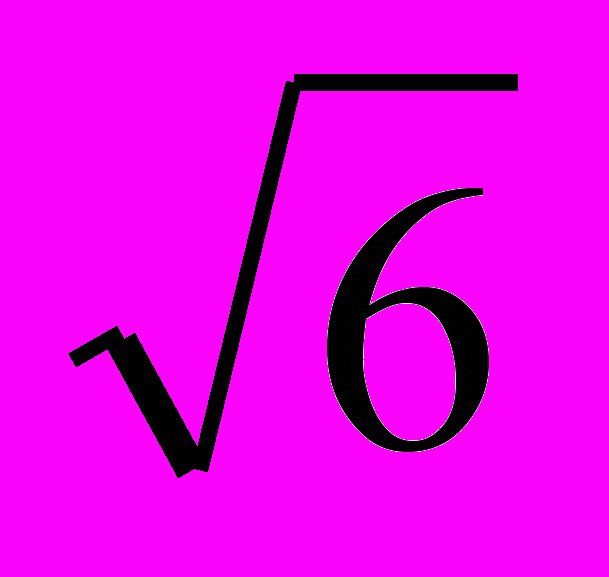 . Ответ: –3 ±
. Ответ: –3 ± 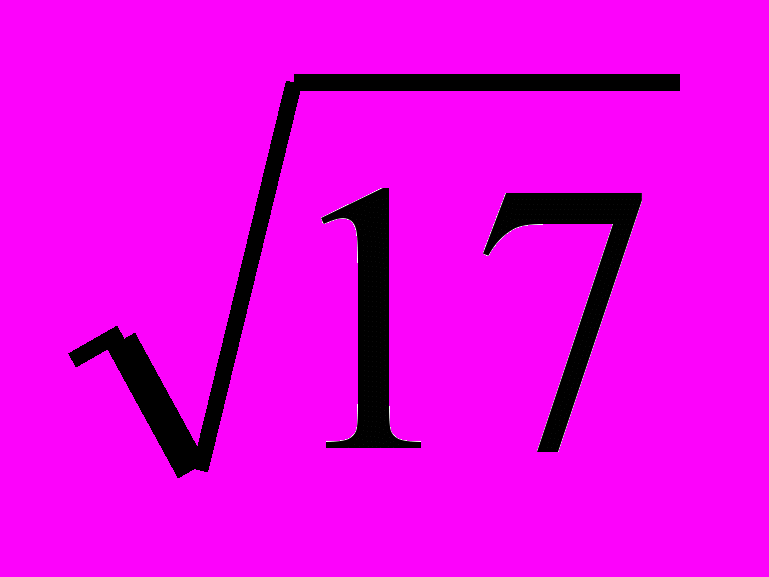 , –3 ±
, –3 ± 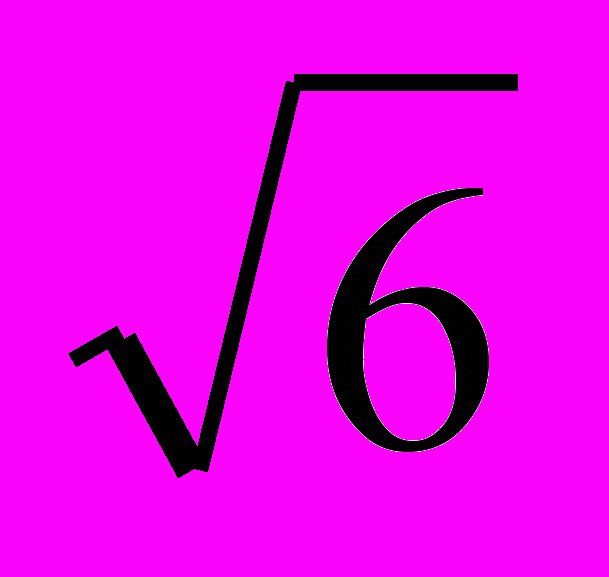 .
.- Изучение нового материала.
а) Объяснение нового материала.
Решить уравнение: (2 х2 + 3)2 – 12 (2 х2 + 3) + 11 = 0.
Учащиеся пытаются раскрыть скобки.
Является ли это уравнение целым?
Умеем мы решать целые уравнения?
Ваши предложения.
б) Объяснение материала учителем.
- Первичное закрепление нового материала.
а) Работа у доски с объяснением (№ 220-б).
б) Работа у доски ( 4 человека, № 220-в,г, остальные работают на месте).
№ 220 (б). (t2 – 2 t)2 – 3 = 2 (t2 – 2 t),
t2 – 2 t = у,
у2 – 2 у – 3 = 0,
у1 = 3, у2 = – 1,
t2 – 2 t = 3 или t2 – 2 t = – 1,
t2 – 2 t – 3 = 0 t2 – 2 t + 1 = 0,
t1 = 3, t2 = – 1, t3 = 1.
Ответ: – 1; 3; 1.
№ 220 (в). (х2 + х – 1) (х2 + 6 х + 2) = 40,
Пусть х2 + х = t,
(t – 1) (t + 2) = 40,
t2 + t – 2 – 40 = 0,
t2 + t – 42 = 0,
t1 = – 7, t2 = 6,
х2 + х = – 7 или х2 + х = 6,
х2 + х + 7 = 0, х2 + х – 6 = 0,
D = 1 – 28 = – 27 < 0, х1 = – 3, х2 = 2.
корней нет. Ответ: –3; 2.
№ 220 (г). (2 х2 + х – 1) (2 х2 + х – 4) + 2 = 0,
Пусть 2 х2 + х = t,
(t – 1) (t – 4) + 2 = 0,
t2 – 5 t + 4 + 2 = 0,
t2 – 5 t + 6 = 0,
t1 = 3, t2 = 2,
2 х2 + х = 3 или 2 х2 + х = 2,
2 х2 + х – 3= 0, 2 х2 + х – 2 = 0,
D = 1 + 24 = 25, D = 1+ 16 = 17,
х1 = (– 1 + 5) / 4 = 1, х3 = (– 1 +
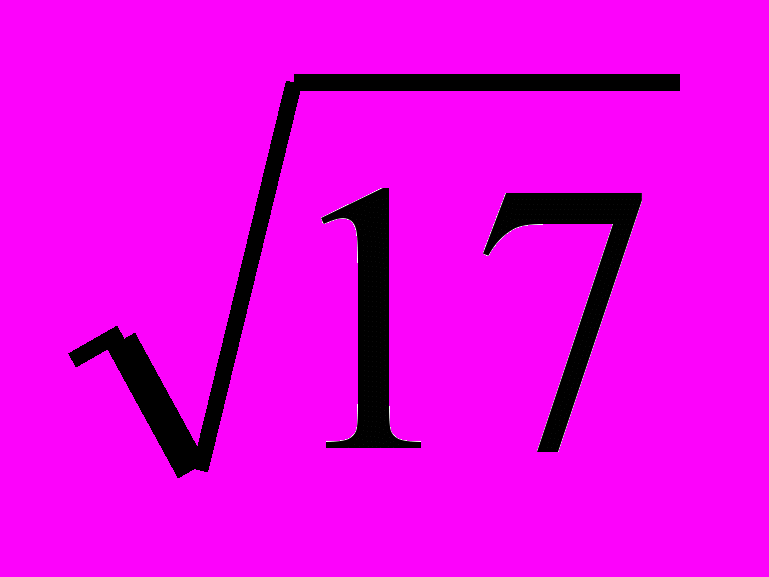 ) / 4,
) / 4,х2 = (– 1 – 5) / 4 = 1,5, х4 = (– 1 –
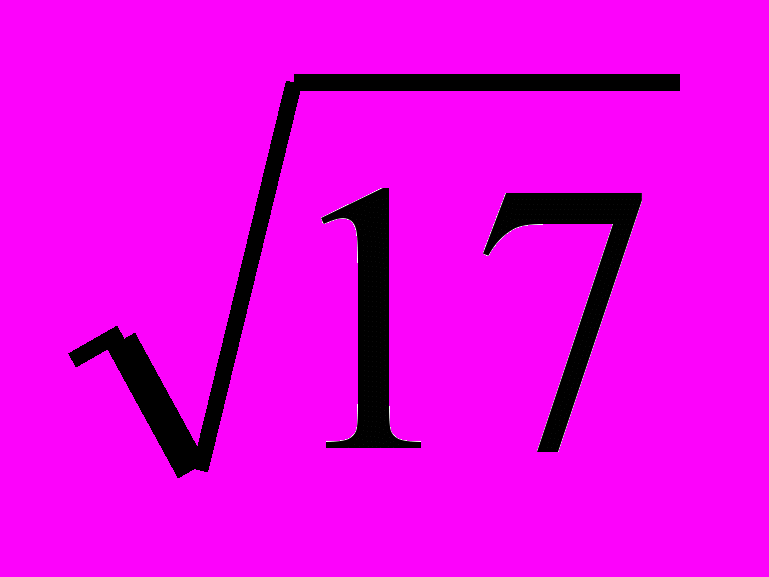 ) / 4.
) / 4.Ответ: 1; 1,5; (– 1 +
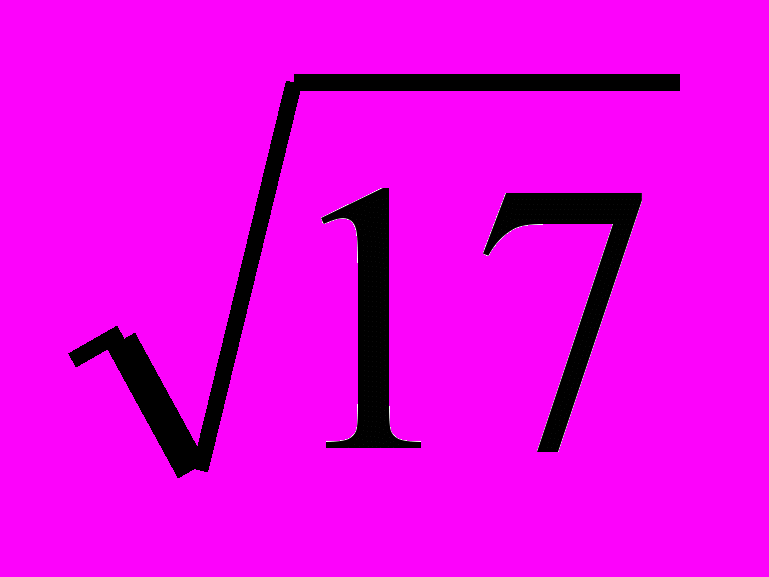 ) / 4; (– 1 –
) / 4; (– 1 –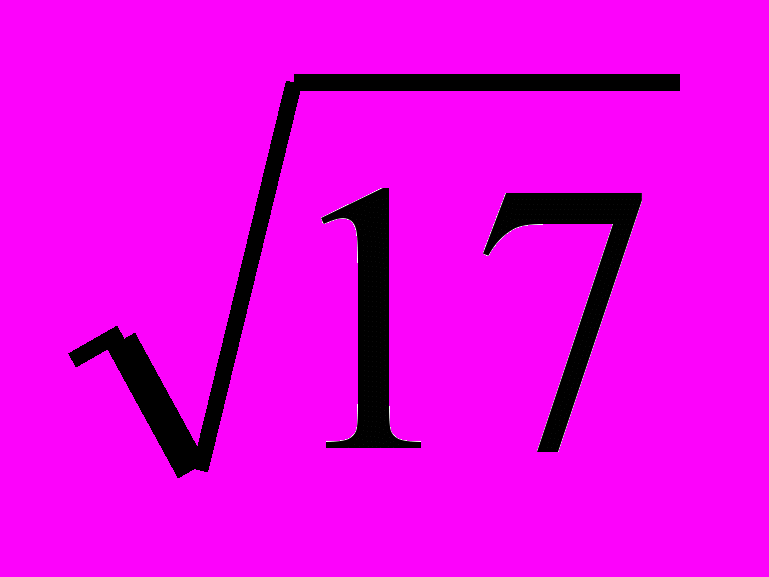 ) / 4.
) / 4.- Задание на дом.
П. 11, пр. 1, № 221, № 295 (б, д-з), по сборнику работа № 7.
- Итог урока.
Выставление оценок.
- Рефлексия.
Отметьте высказывание, которое соответствует вашему состоянию на сегодняшнем уроке.
Обращение к эпиграфу.
Приложение 7
Сводная таблица диагностических показателей №2
| Показатель | Уровень | Количество учащихся данного уровня |
| Уровень сформированности знаний по предмету | Низкий | 1 (4,8 %) |
| Ниже среднего | 2 (9,5 %) | |
| Средний | 7 (33,3%) | |
| Выше среднего | 6 (28,6 %) | |
| Высокий | 5 (23,8 %) | |
| Развитие мышления | Низкий | 1 (4,8 %) |
| Ниже среднего | 2 (9,5 %) | |
| Средний | 8 (38,1 %) | |
| Выше среднего | 4 (19,0 %) | |
| Высокий | 6 (23,8 %) | |
| Отношение к предмету | Низкий | - (0 %) |
| Ниже среднего | 1 (4,8 %) | |
| Средний | 4 (19,0 %) | |
| Выше среднего | 6 (28,6 %) | |
| Высокий | 10 (47,6 %) |
