К. Д. Ушинский Условия возникновения опыта моу «Репяховская средняя общеобразовательная школа»
| Вид материала | Документы |
СодержаниеНомер задания VI. Проверка самостоятельной работы. VIII. Итог урока. Ответ: ДОБРОТА.Учитель. |
- Приказ №165 от «7» декабря 2011 г. «Об итогах районного конкурса сочинений «И отблеск, 24.24kb.
- Приказ №163 от «7» декабря 2011 г. «Об итогах районного конкурса мозаичных картин «Любо, 15.63kb.
- Порядок и условия оплаты труда работников моу «Трудармейская средняя общеобразовательная, 328.3kb.
- И. Э. Торкунова директор моу «Школа №8» моу «Средняя общеобразовательная школа №8», 1447.31kb.
- Моу «Тишанская средняя общеобразовательная школа Волоконовского района Белгородской, 216.48kb.
- План работы моу «Репяховская основная общеобразовательная школа» на зимних каникулах, 161.25kb.
- Публичный доклад директора моу «Средняя общеобразовательная школа №16» г. Серпухова, 616.15kb.
- Доклад моу «Средняя общеобразовательная школа №39», 659.53kb.
- Моу «Саскылахская средняя общеобразовательная школа» Анабарский национальный(долгано-эвенкийский)улус, 362kb.
- Доклад моу «Средняя общеобразовательная школа №24 п. Бира», 1155.85kb.
Тест № 2.
Номер задания | 1 | 2 | 3 | 4 |
| Ответ | | | | |
- Верно ли, что все предложенные здесь пары уравнений равносильны?
1

 .
. 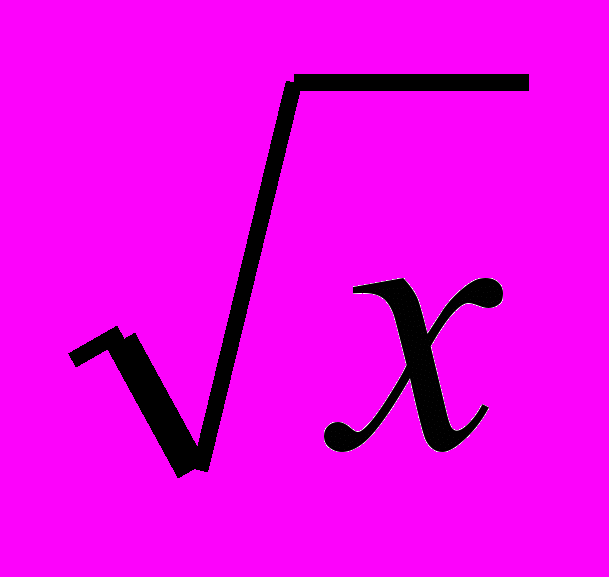 = 2 и х = 4; 2. √ х2 и х = 2; 3.
= 2 и х = 4; 2. √ х2 и х = 2; 3. 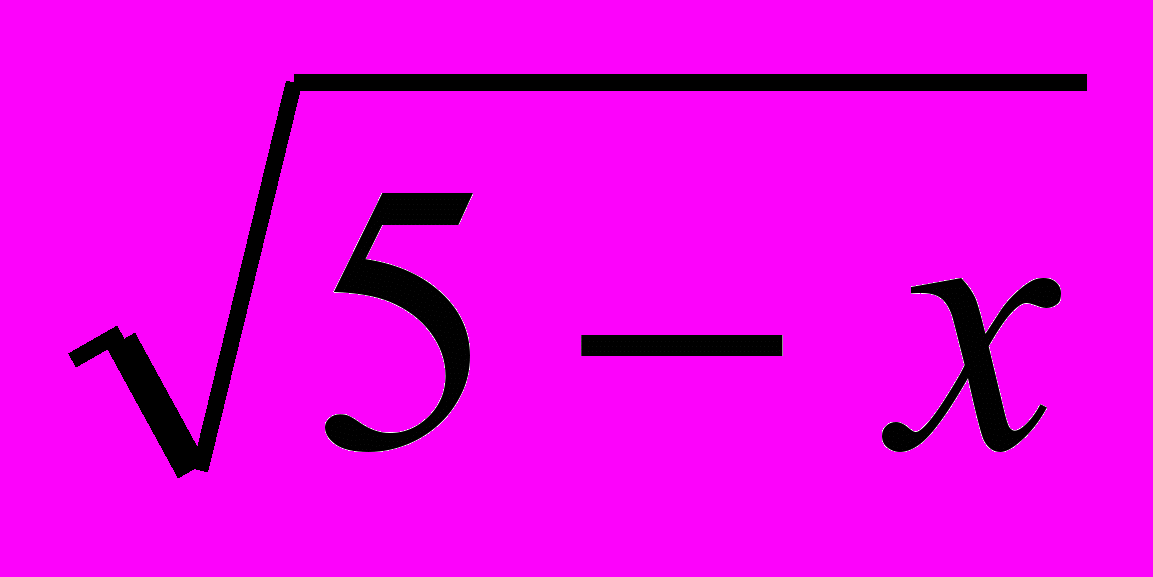 и 5 – х = х2; 4. х – 3 =
и 5 – х = х2; 4. х – 3 = 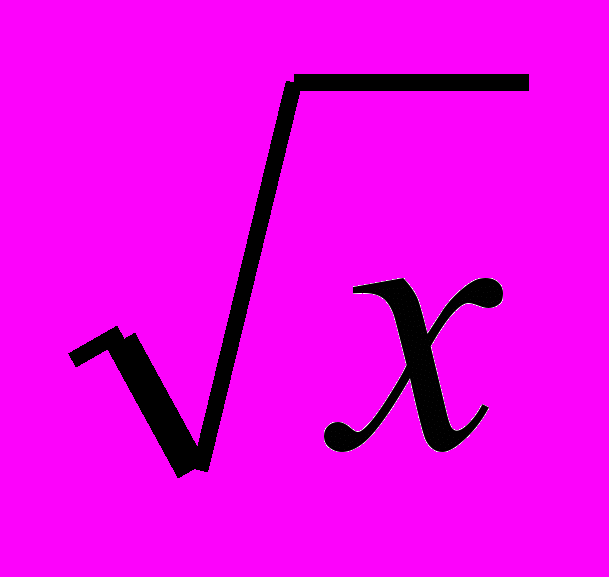 и 4х – 3 = 4√2.
и 4х – 3 = 4√2.Ответы: 1. да; 2. нет; 3. нет; 4. да.
- Решить уравнения:
1

 .
. 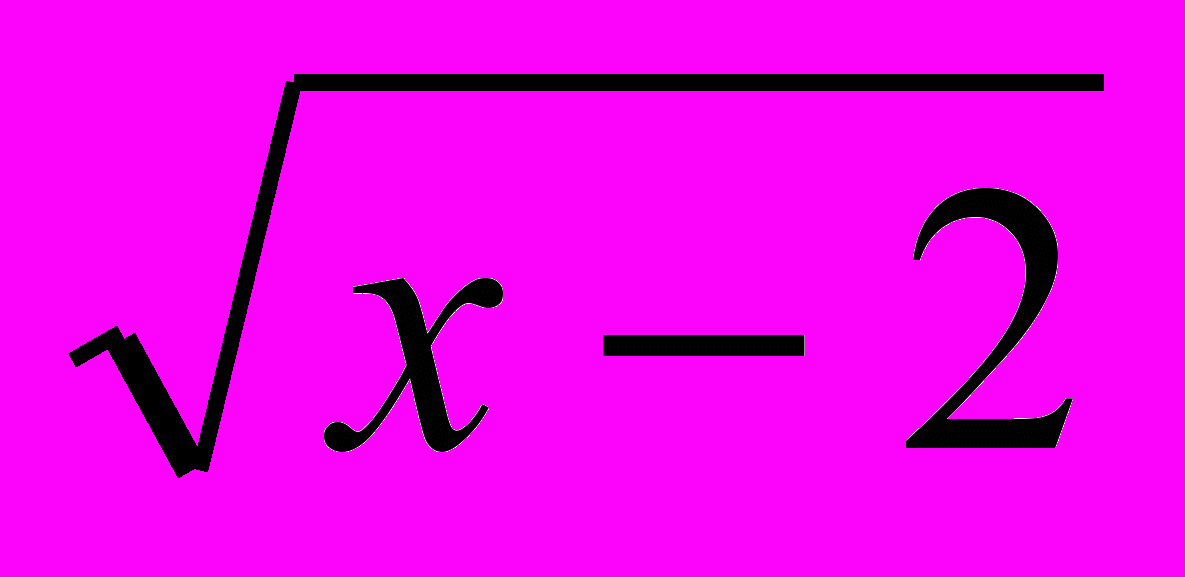 = 9; 2. √ х2 = 5; 3.
= 9; 2. √ х2 = 5; 3.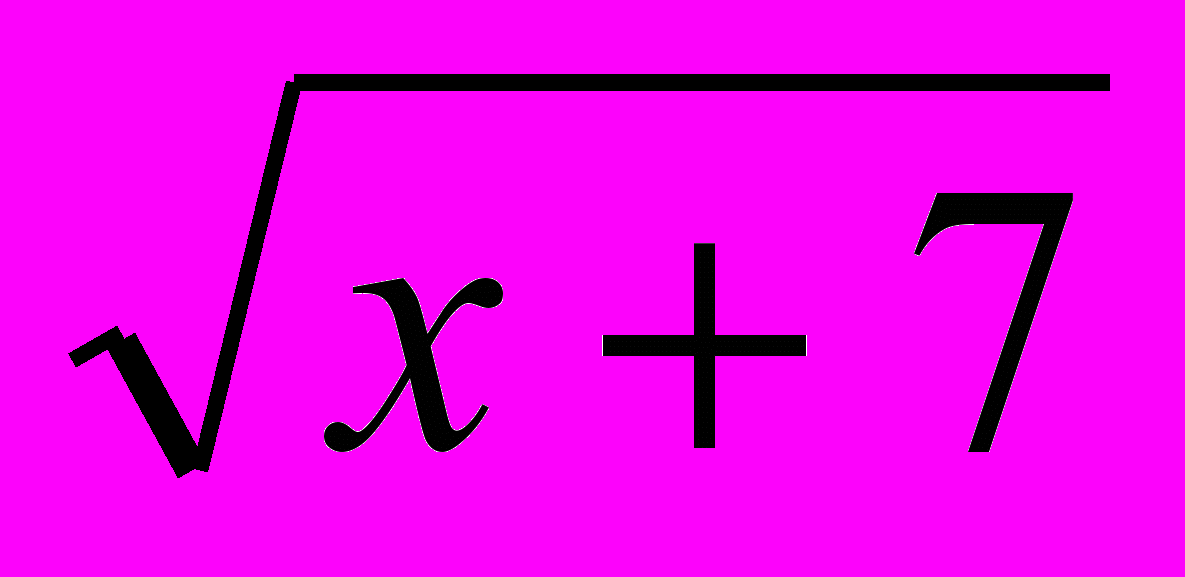 = – 3; 4. 3√1 – х2 = – 2.
= – 3; 4. 3√1 – х2 = – 2.Ответы: 1. 83; 2. ± 5; 3. Ø; 4. ± 3.
в) Повторение общих приёмов решения уравнений.
Объясните, в чём заключается:
- метод разложения на множители (Этот метод заключается в том, что уравнение f(х) = g(х) = 0 можно заменить совокупностью уравнений f(х) = и g(х) = 0.);
- метод введения новой переменной (Этот метод заключается в том, что если уравнение f(х) = 0 сводится к уравнению h(g(x)) = 0, то нужно ввести новую переменную.);
- использование свойств функций (Пусть имеется уравнение f(х) = g(х). Если одна из функций возрастает, а другая – убывает, то исходное уравнение либо не имеет корней, либо имеет единственный, который легко угадывается.);
- использование графиков (Пусть имеется уравнение f(х) = g(х). Нужно построить графики функций у = f(х) и у = g(х) и найти все точки их пересечения, абсциссы этих точек и являются корнями исходного уравнения.).
г) Устная работа.
Объяснить, не решая, имеют ли данные уравнения решения.
1.
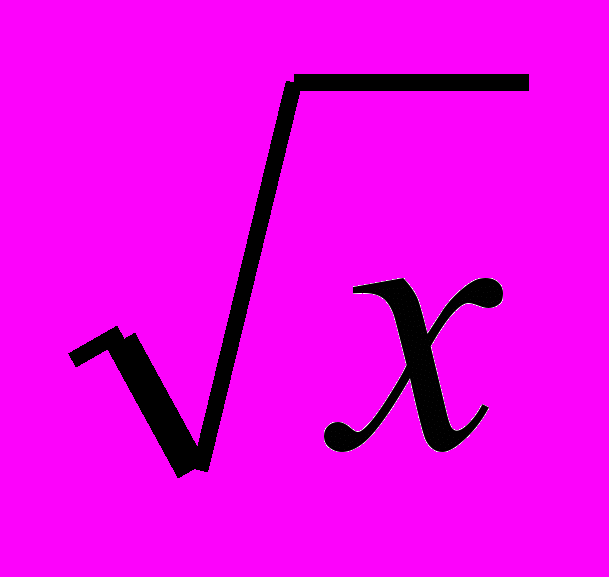 = 2 х – 1 – х2 (II группа). 2. 4
= 2 х – 1 – х2 (II группа). 2. 4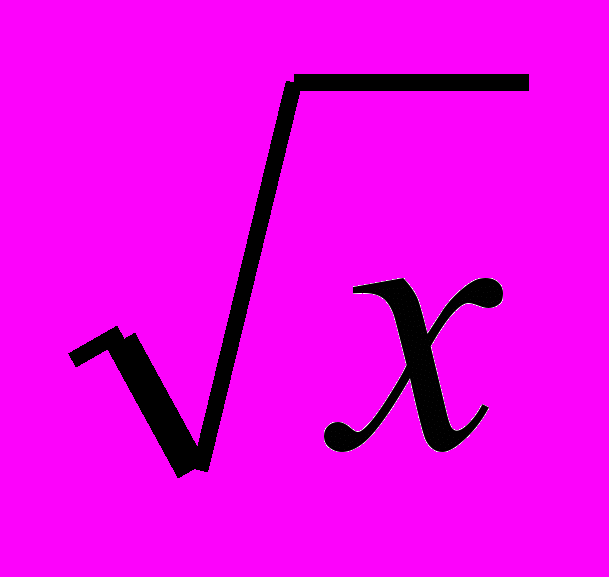 + 2 = 0 (I группа).
+ 2 = 0 (I группа).IV. Систематизация и обобщение знаний (работа с учителем).
Цель: проверить умения учащихся применять различные методы решения иррациональных уравнений.
№ 1. Метод введения новой переменной.
√
 х2 + 1 – 2 х – 6
х2 + 1 – 2 х – 6 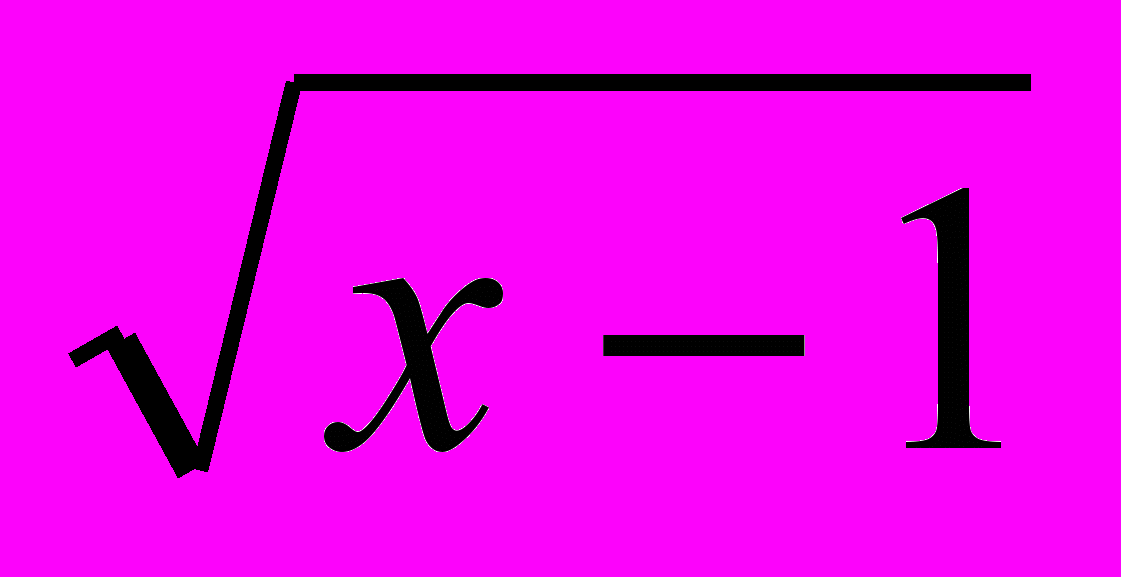 = 7;
= 7;√
 х2 – 2 х + 1 – 6
х2 – 2 х + 1 – 6 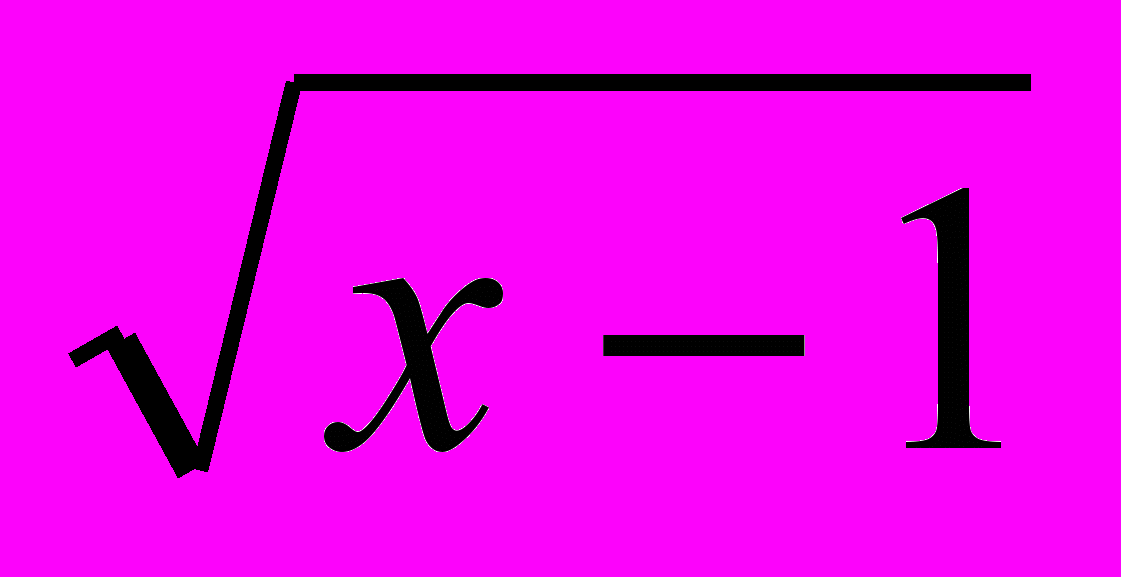 = 7;
= 7;√
 (х – 1)2 – 6
(х – 1)2 – 6 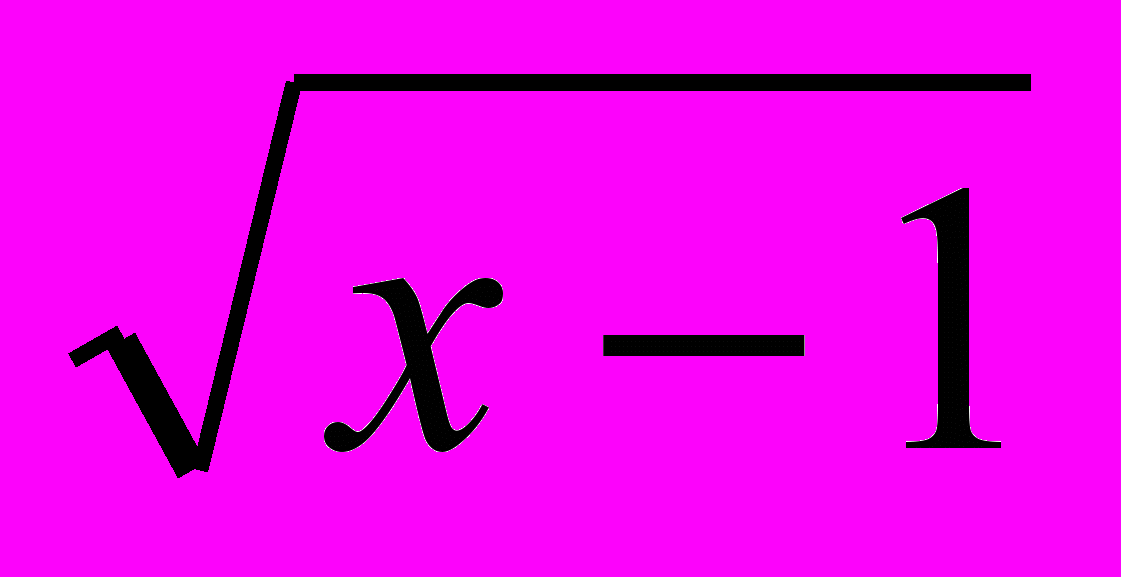 = 7;
= 7;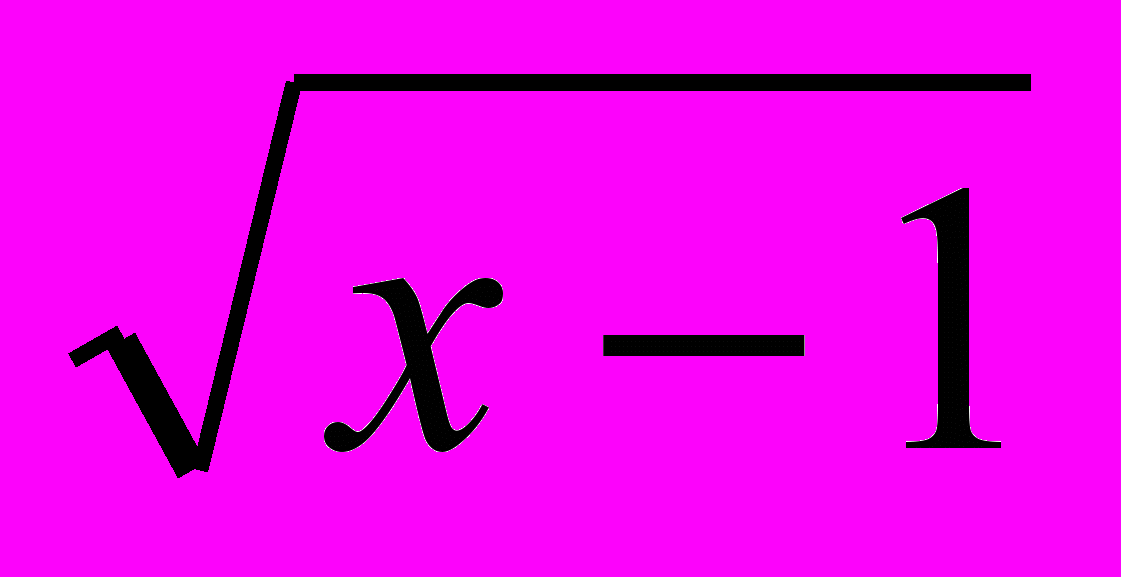 = а ≥ 0;
= а ≥ 0;а2 – 6 а – 7 = 0;
а = 7,
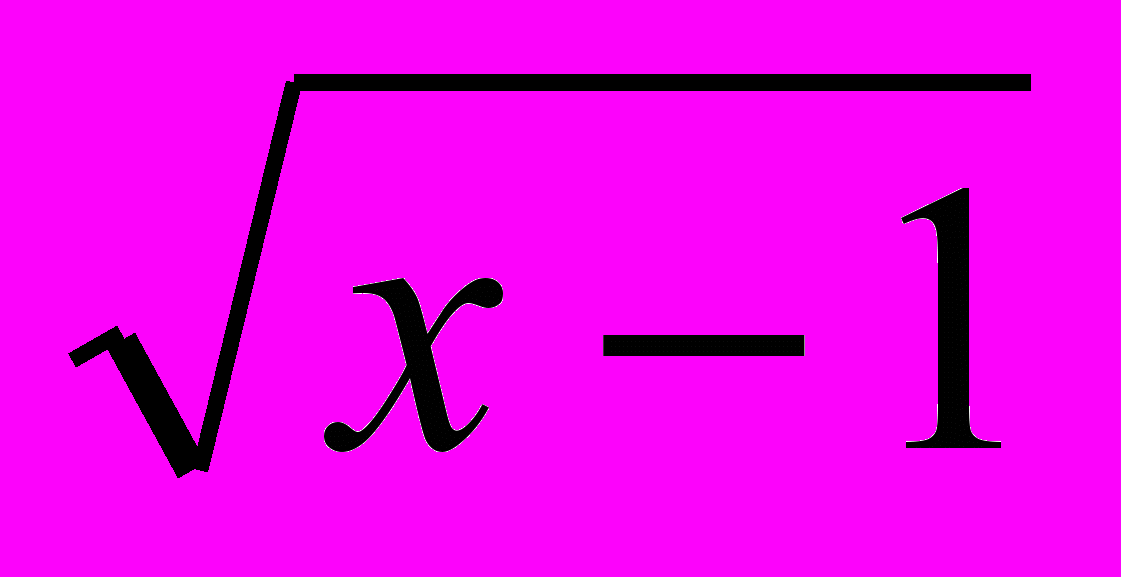 = 7, х = 50;
= 7, х = 50;а = –1 не подходит
Ответ: 50.
2-й способ.
√
 х2 + 1 – 2 х = 7 + 6
х2 + 1 – 2 х = 7 + 6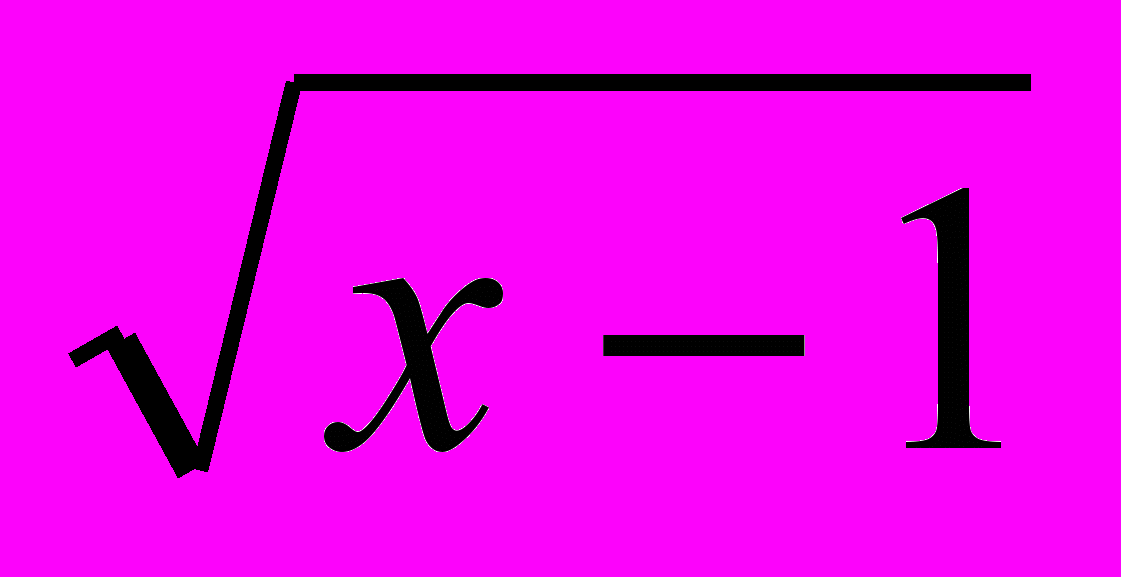 ;
;х2 – 2 х + 1 = 49 + 84
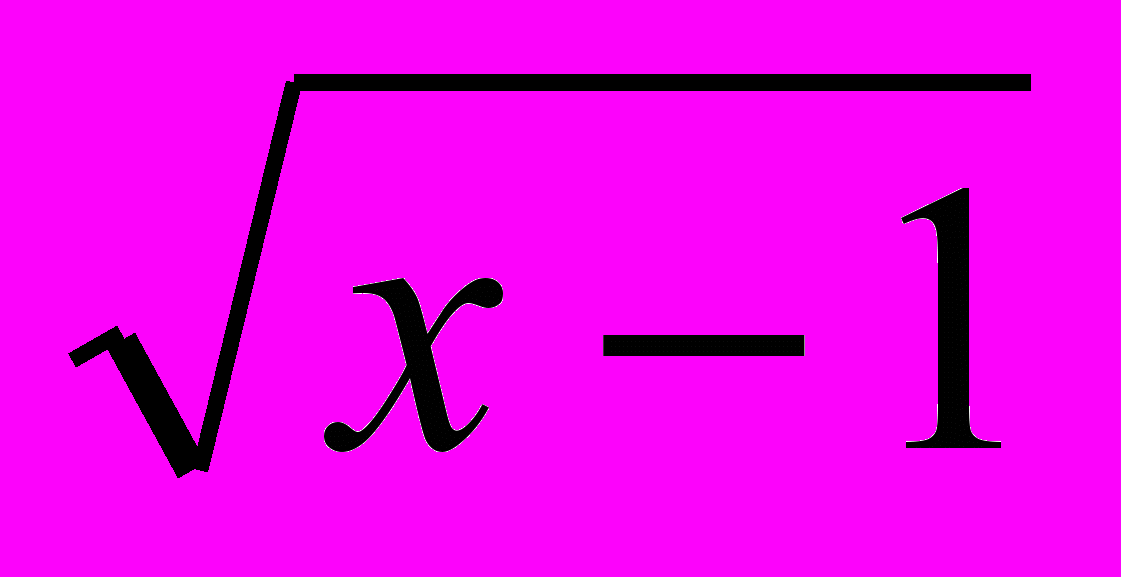 + 36 х – 36 с введением новой переменной
+ 36 х – 36 с введением новой переменной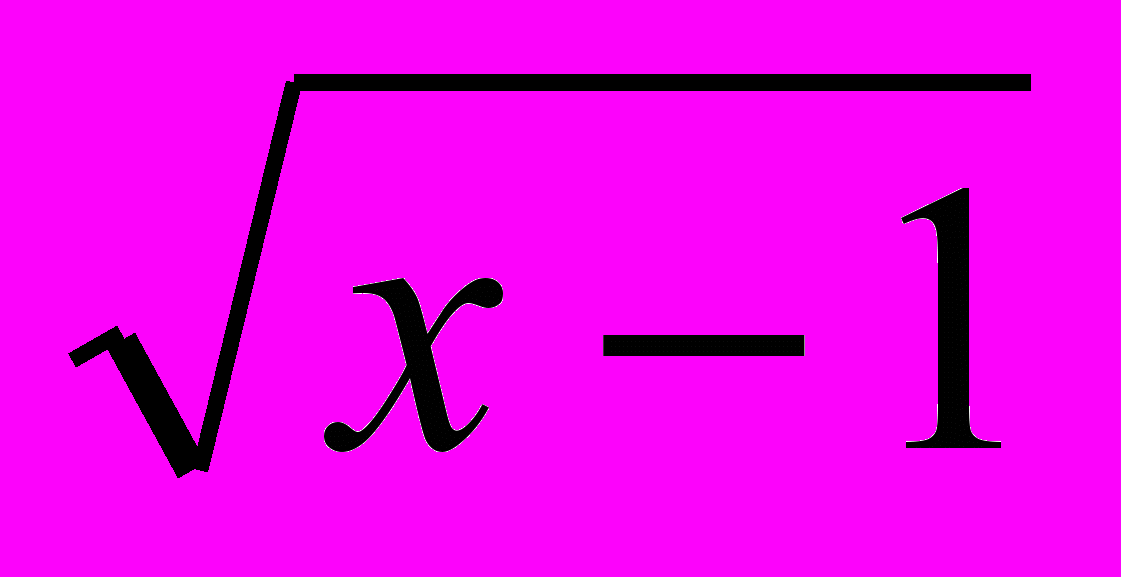 = а ≥ 0.
= а ≥ 0.№ 2. Использование нескольких методов одновременно.
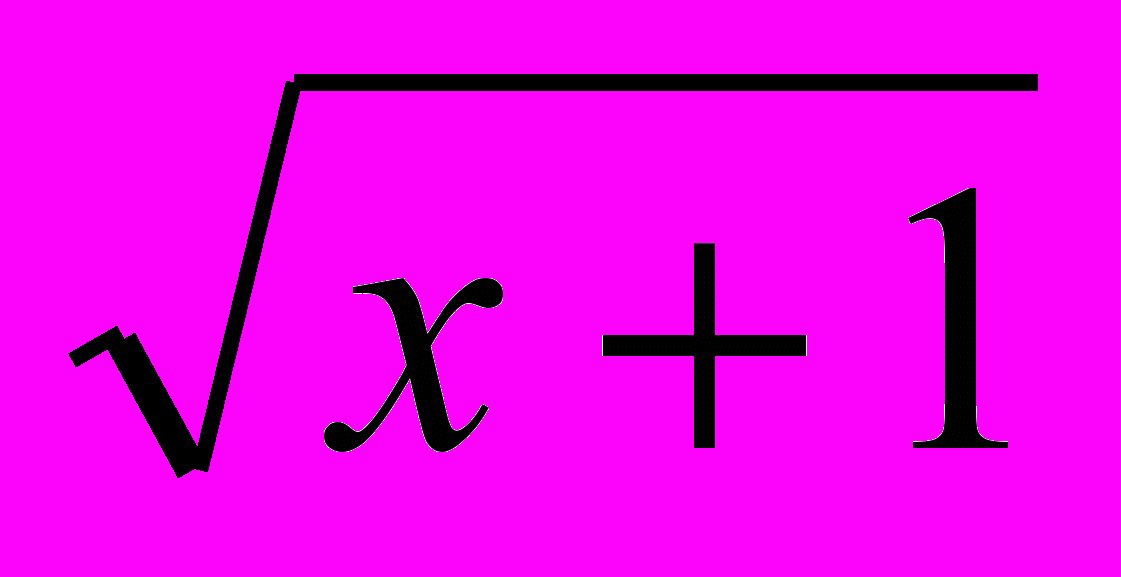 +
+ 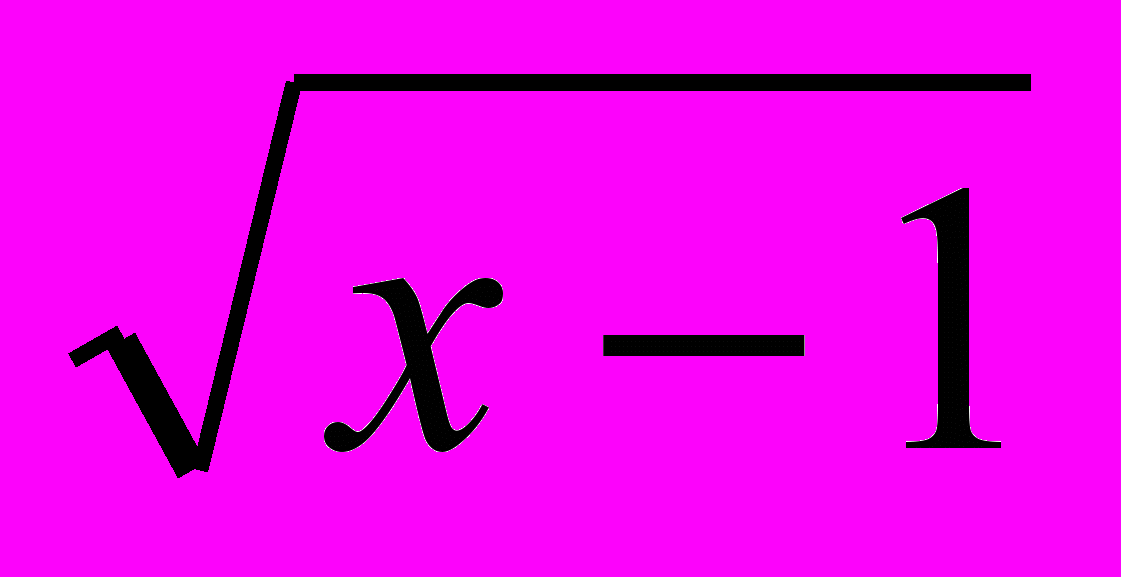 =
= 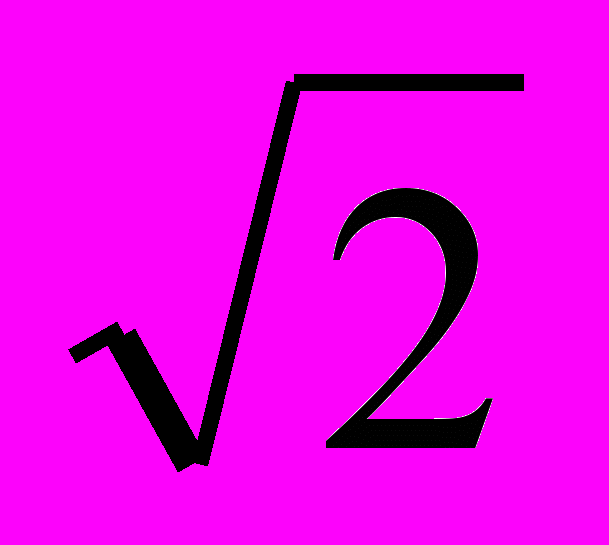 ;
;О.Д.З.: х ≥ 1, х ≥ – 1; х ≥ 1;
2
 х + 2 √ х2 – 1 = 2;
х + 2 √ х2 – 1 = 2;√
 х2 – 1 = 1 – х, 1 – х ≥ 0, х ≤ 1.
х2 – 1 = 1 – х, 1 – х ≥ 0, х ≤ 1.Ответ: х = 1.
- Самостоятельная работа.
I группа. Решить уравнения:
а
 ) х – 3
) х – 3 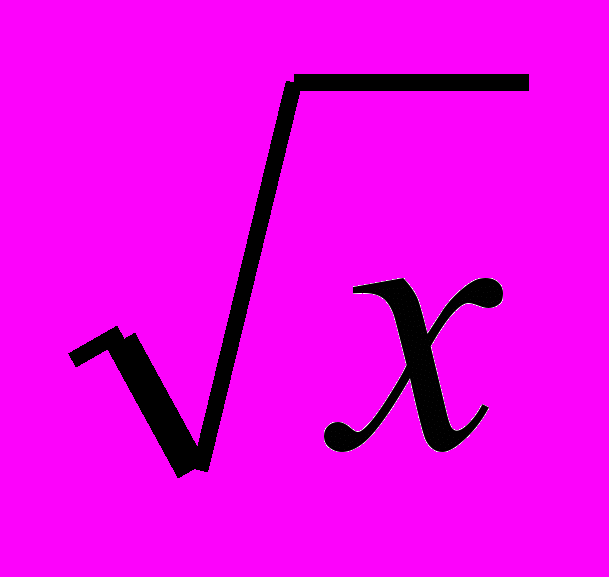 = 4; б) │
= 4; б) │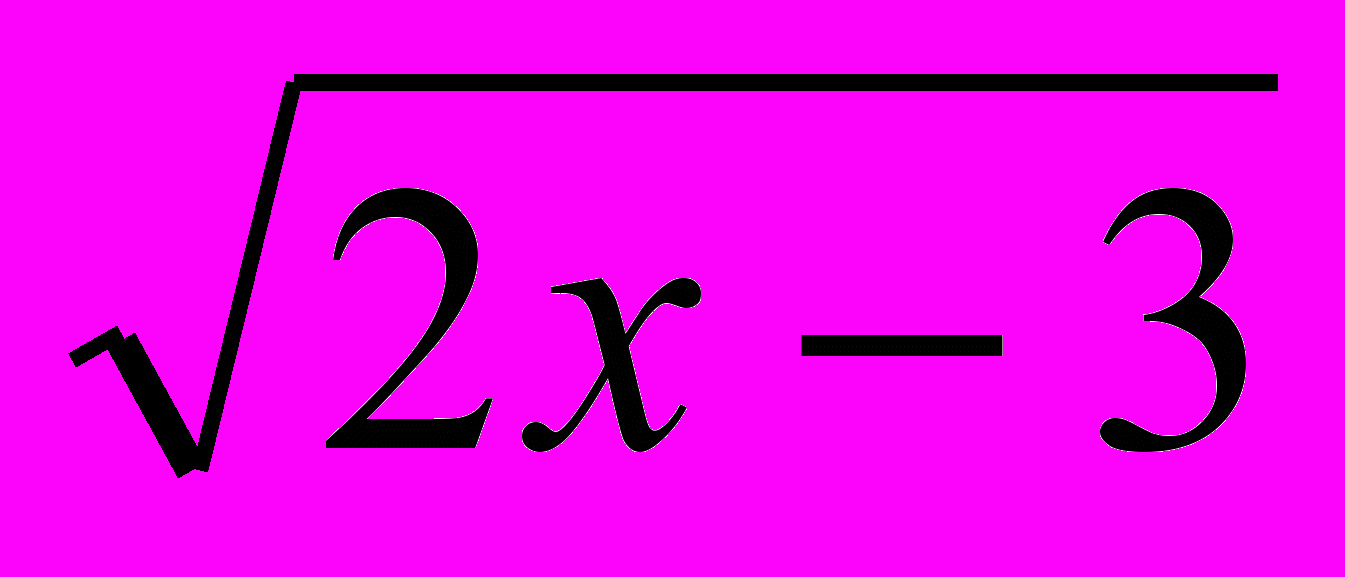 – 1│= 2; в) √4 – 5 х │х + 3│ – 2 = х.
– 1│= 2; в) √4 – 5 х │х + 3│ – 2 = х.Решение:
а) х – 3
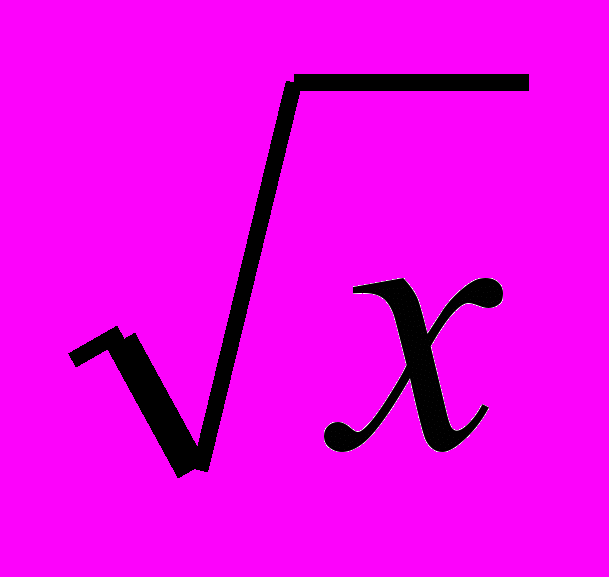 – 4 = 0;
– 4 = 0;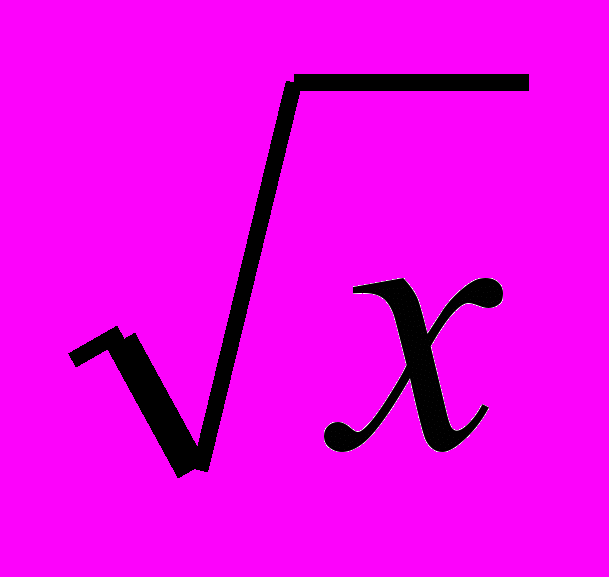 = t, t ≥ 0;
= t, t ≥ 0;t2 – 3 t – 4 = 0;
t1 = 4, t2 = – 1 (не удовлетворяет);
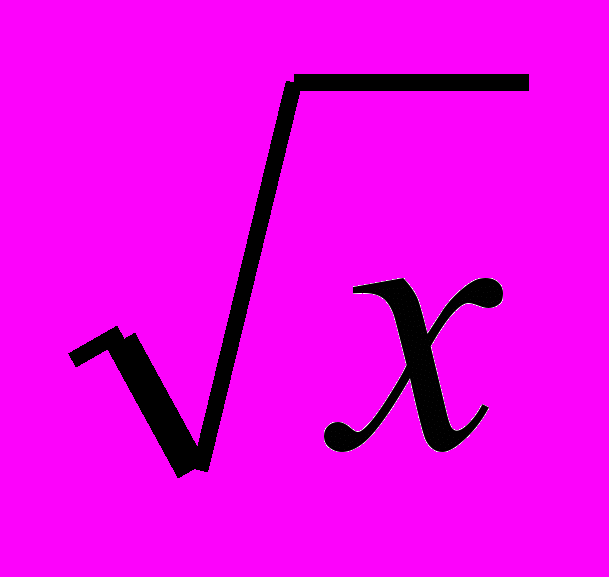 = 4; х = 16.
= 4; х = 16.Ответ: 16.
б)
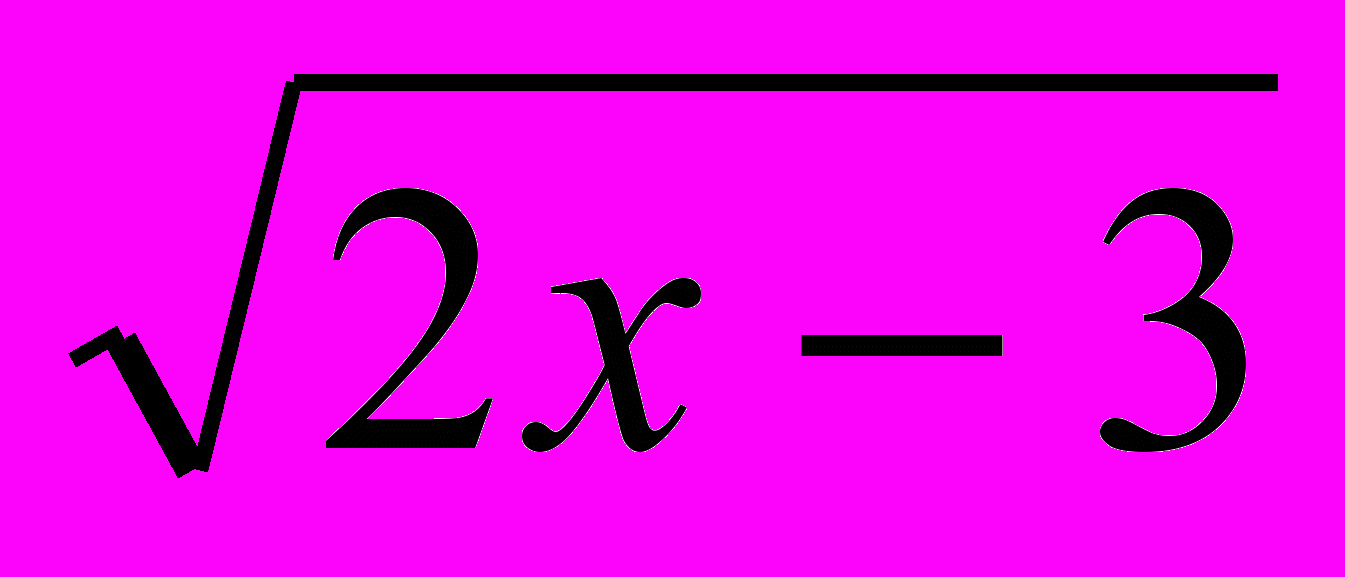 – 1 = 2;
– 1 = 2; 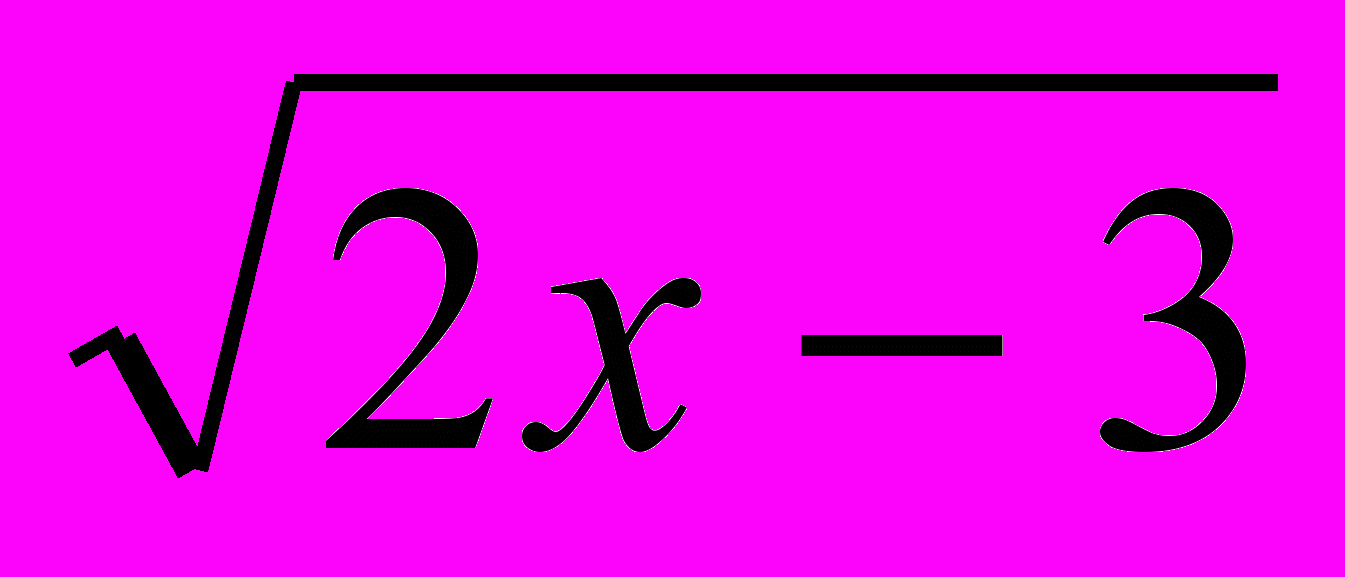 = 3; 2 х – 3 = 9; 2 х = 12; х = 6;
= 3; 2 х – 3 = 9; 2 х = 12; х = 6; 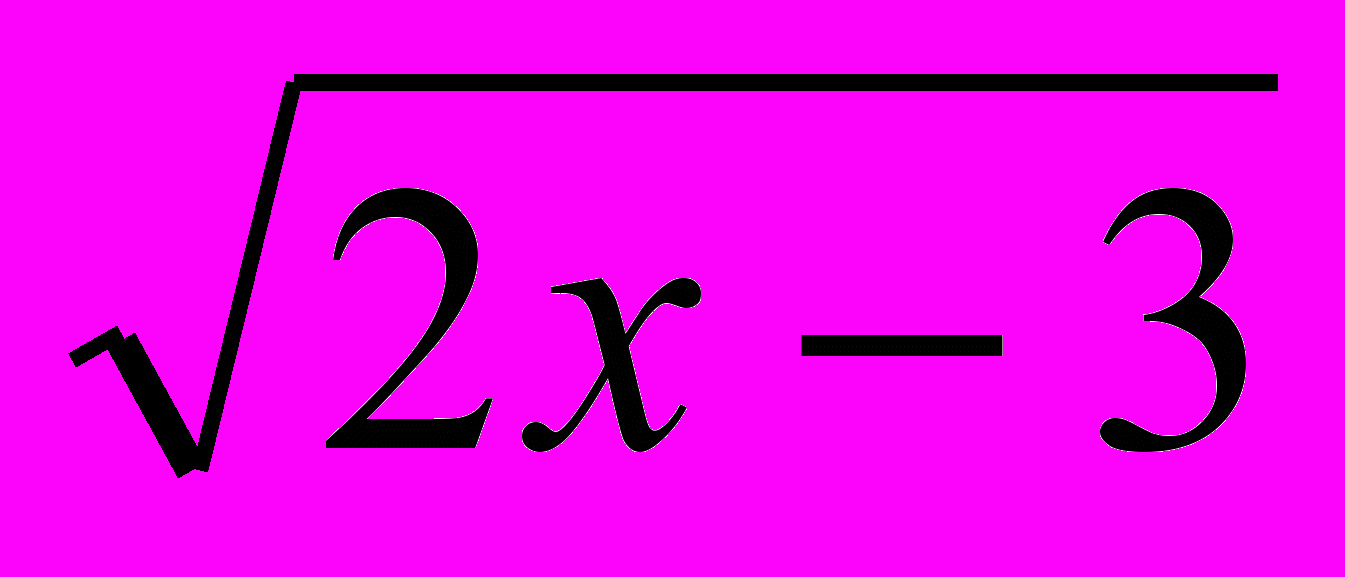 – 1 = – 2;
– 1 = – 2; 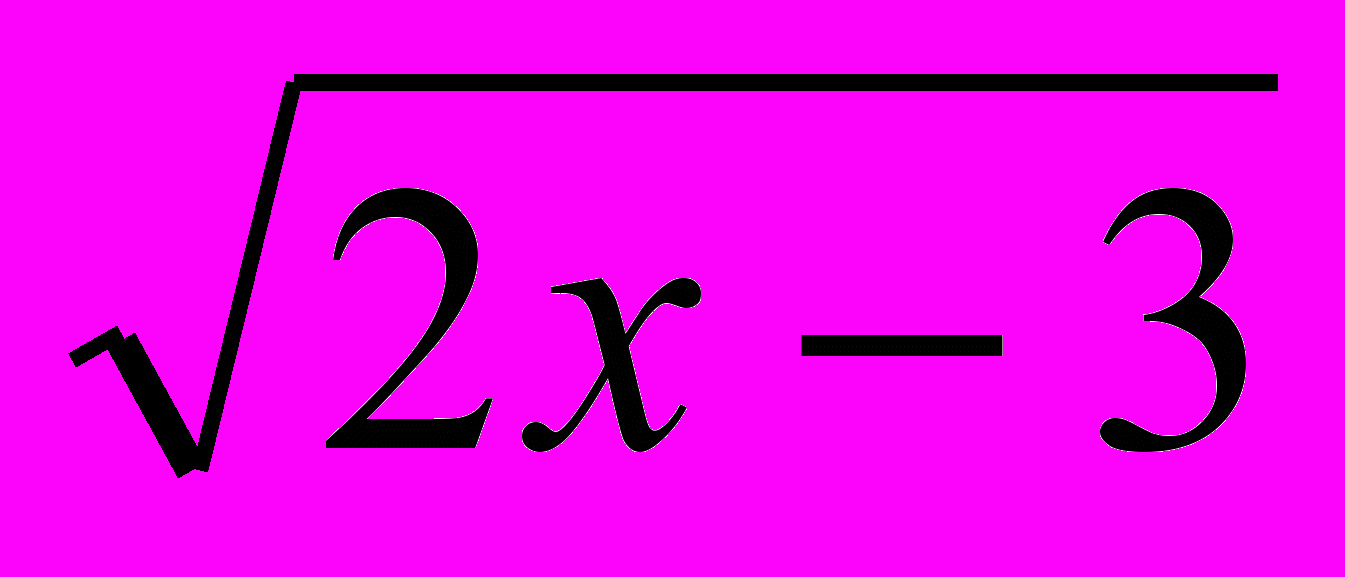 = – 1; Ø.
= – 1; Ø.Ответ: 6.

в) √4 – 5 х│х + 3│= х + 2;
О.Д.З.: х + 2 ≥ 0; х ≥ – 2;
│
 х + 3│= х + 3 однозначно;
х + 3│= х + 3 однозначно;√4 – 5 х (х + 3) = х + 2;
√
 4 – 5 х2 – 15 х = х + 2;
4 – 5 х2 – 15 х = х + 2;(х + 2)2 = 4 – 5 х2 – 15 х;
х2 + 5 х + 4 = 4 – 5 х2 – 15 х;
6 х2 + 19 х = 0;
х (6 х + 19) = 0;
х = 0, х = – 19/6 (посторонний корень).
Ответ: 0.
II группа. Решить уравнения:
а
 )
) 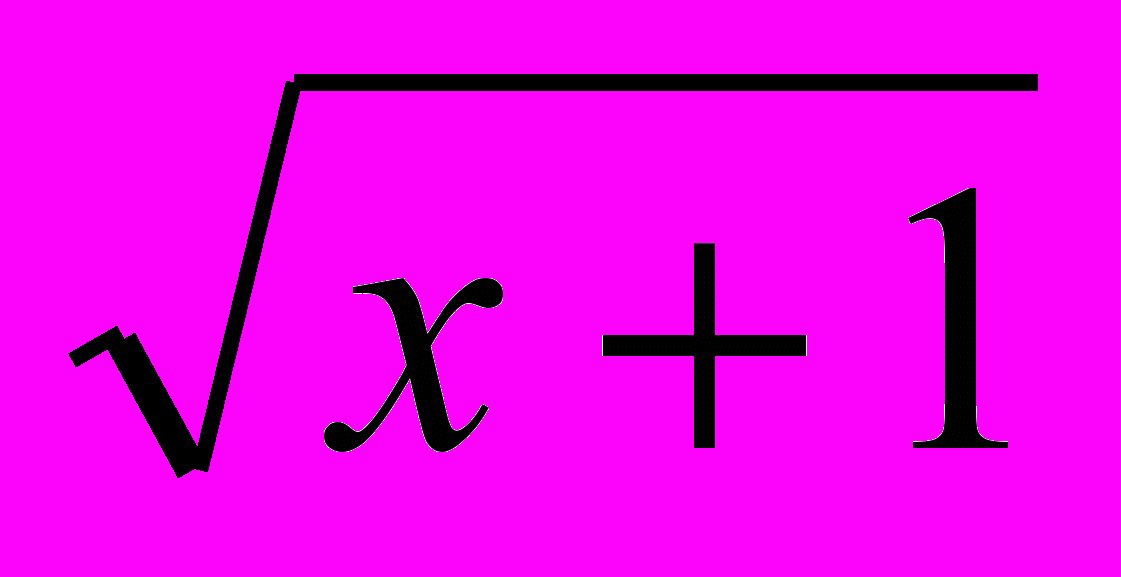 = х – 5; б) √х2 + 5 = 2; в) х +
= х – 5; б) √х2 + 5 = 2; в) х + 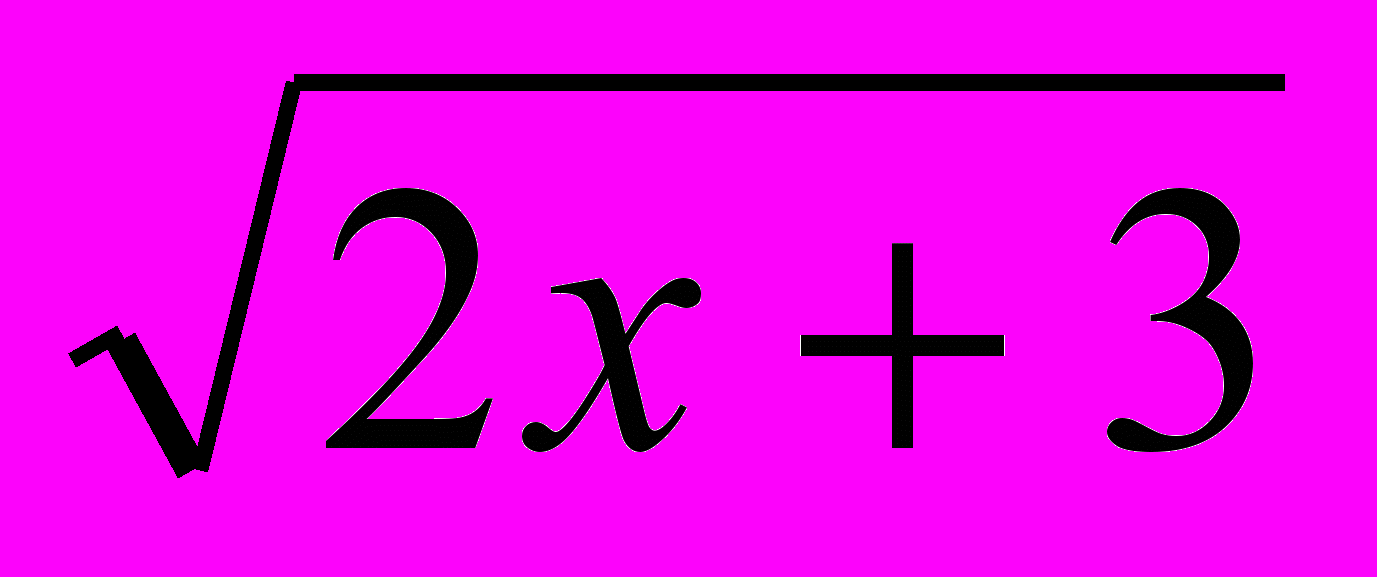 = 6.
= 6.VI. Проверка самостоятельной работы.
Заслушивание объяснений учащихся.
VII. Домашнее задание.
КИМы (на неделю), карточки (выборочные задания).
Ч




 асть А. Решить уравнения: х – 2
асть А. Решить уравнения: х – 2 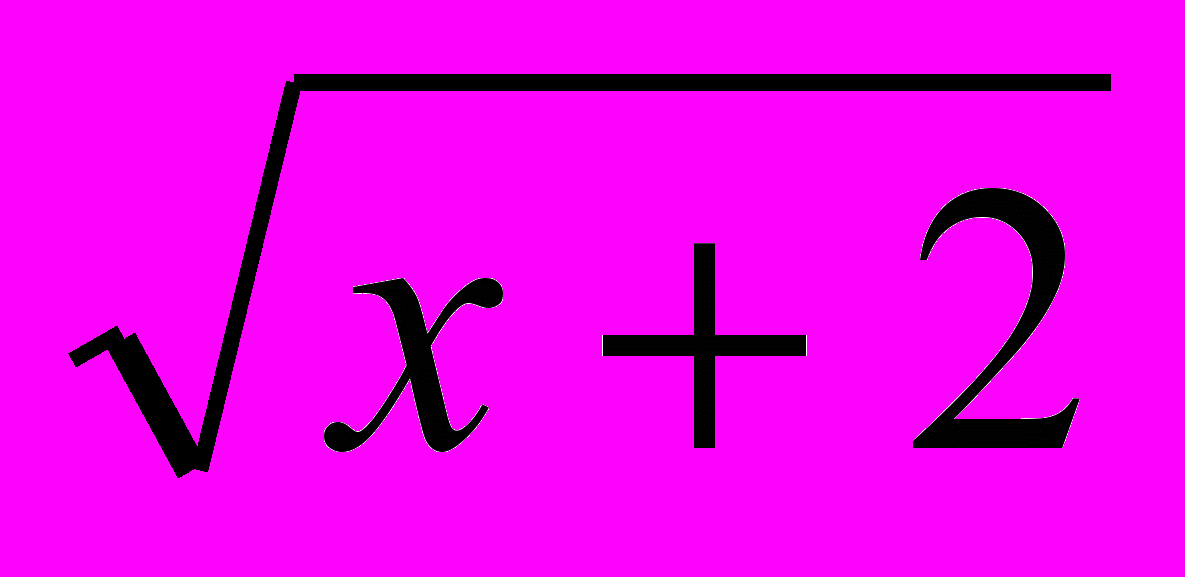 + 3 = 0; √2 х2 + 5 х = √ х2 – 6.
+ 3 = 0; √2 х2 + 5 х = √ х2 – 6.Часть В. Решить уравнения: √ х3 – 5 х + 4 = х – 2; √ х2 – 2 х + 2 + log3 √ х2 – 2 х + 10 = 2.
Ч

 асть С. Решить уравнения: 4
асть С. Решить уравнения: 4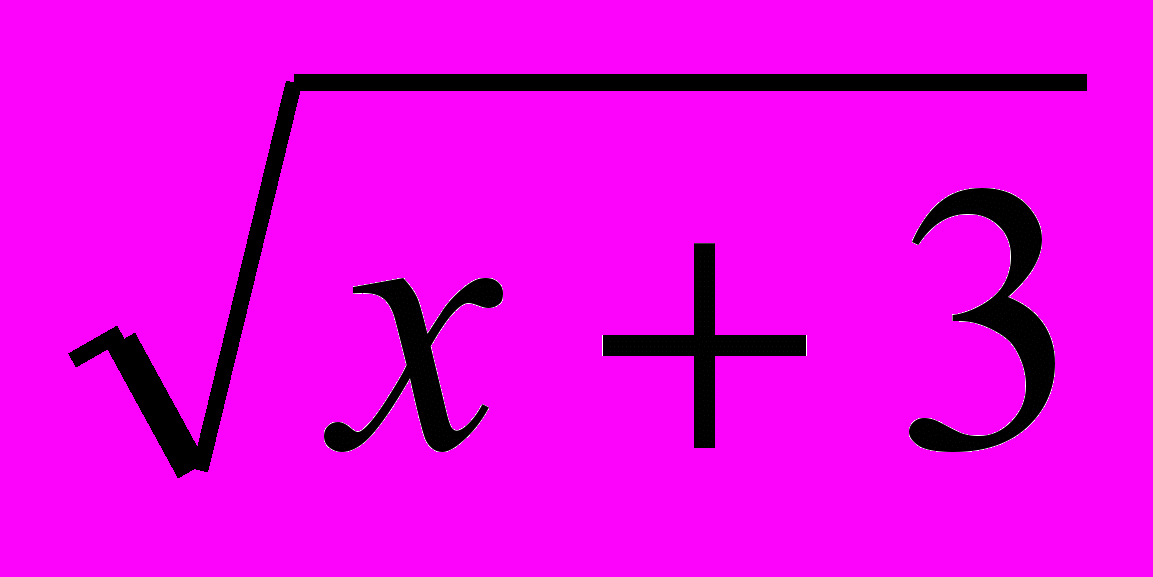 + 4
+ 4 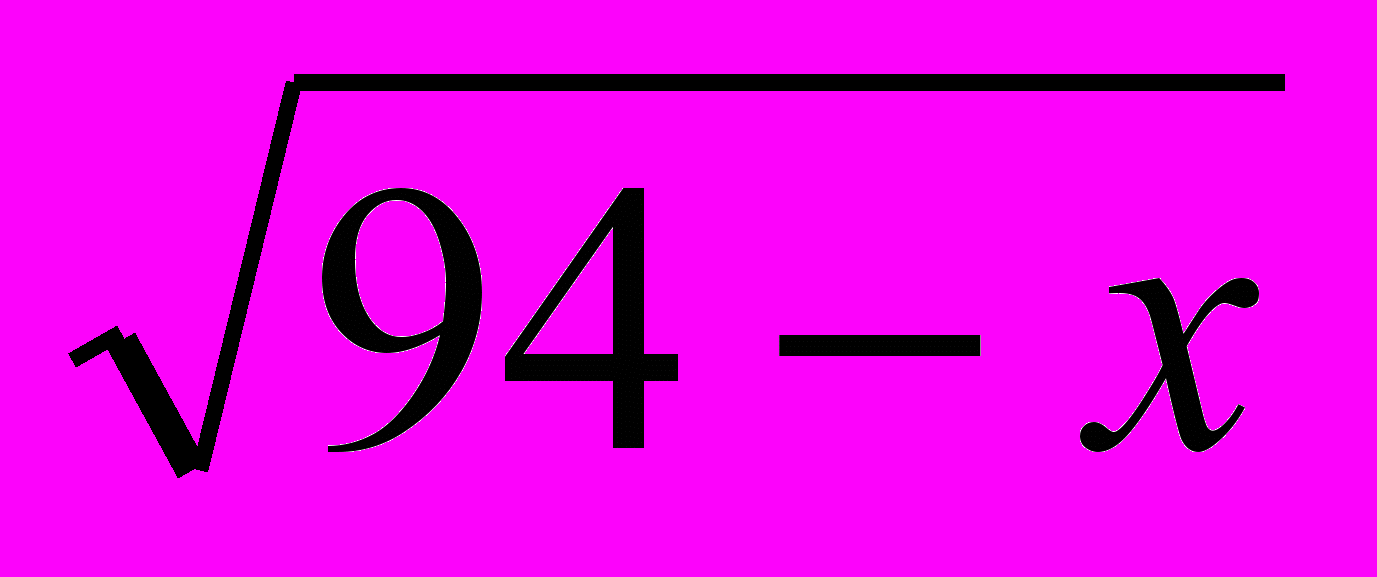 = 5;
= 5;√ х – 2 +
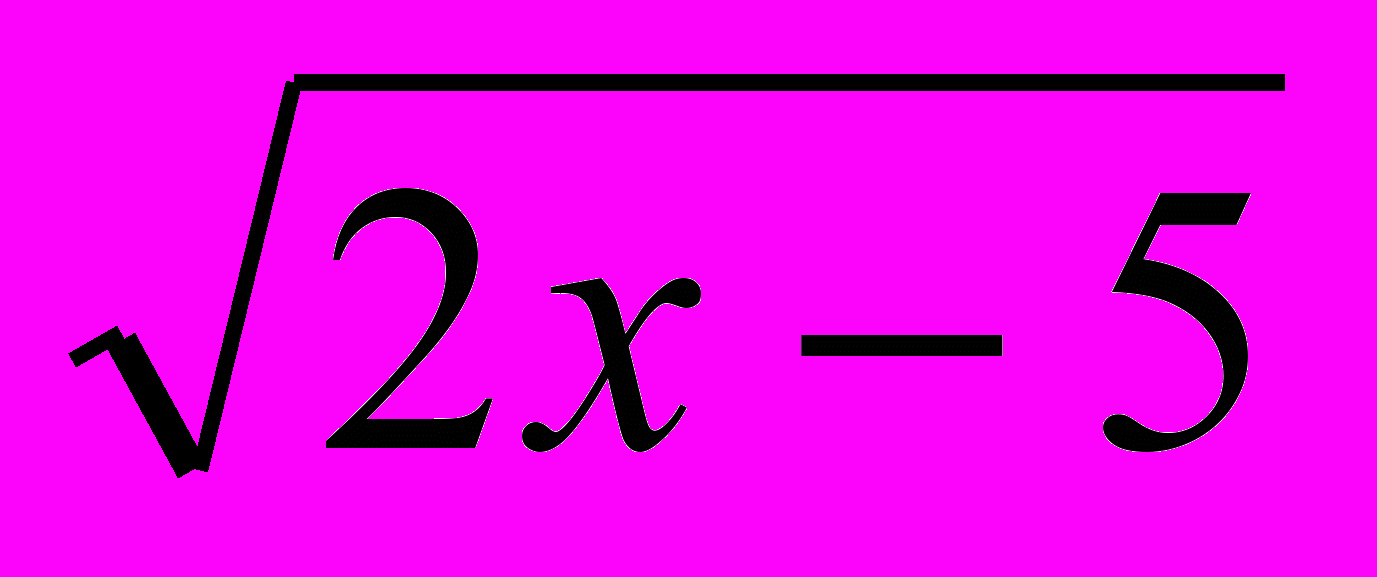 + √ х + 2 + 3
+ √ х + 2 + 3 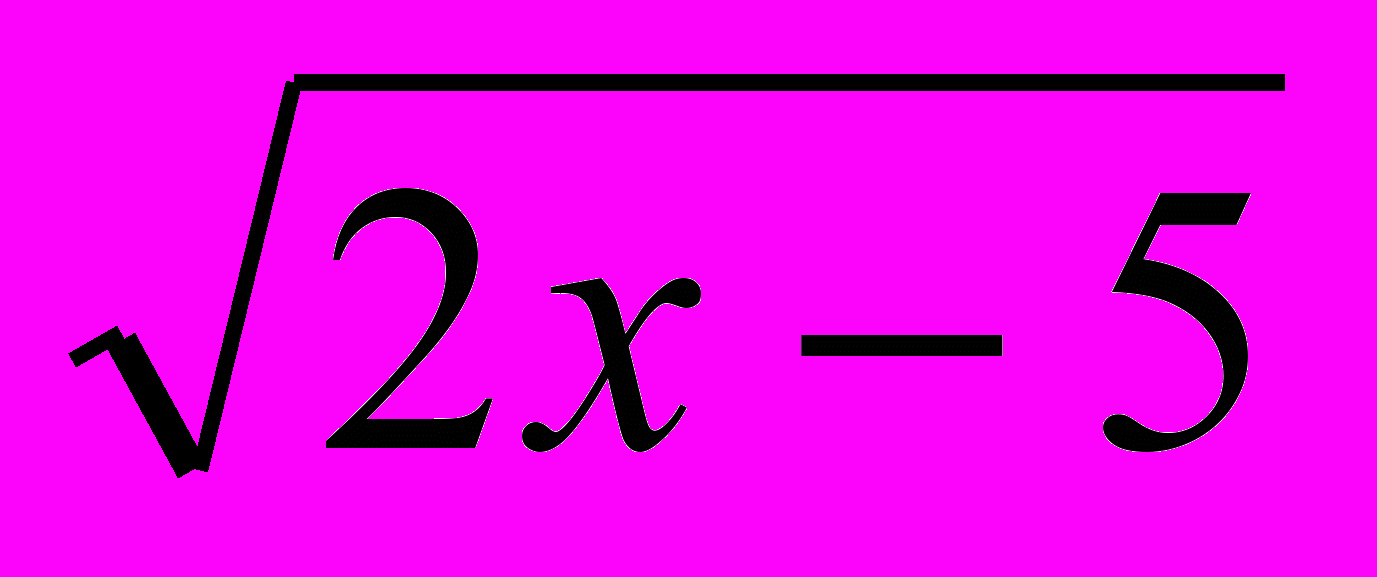 = 7
= 7 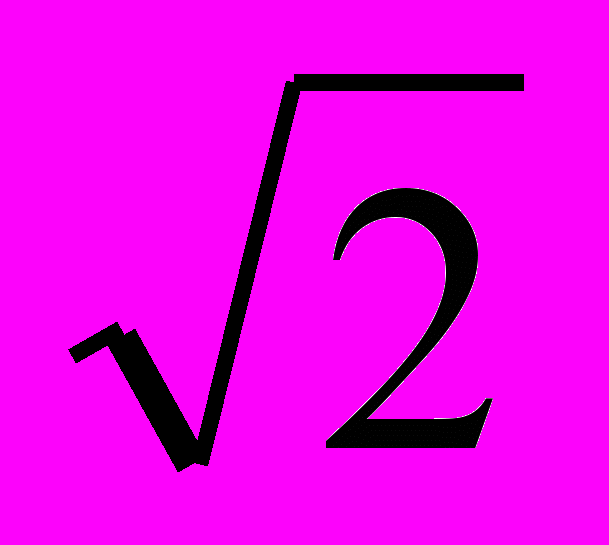 .
.Три качества – обширные знания, привычка мыслить и благородство чувств – необходимы для того, чтобы человек был образованным в полном смысле слова. (Чернышевский.)
VIII. Итог урока.
Карточки учёта.
VIII. Рефлексия.
Я усвоил тему.
Я недостаточно усвоил тему, но смогу самостоятельно разобраться.
У меня возникли трудности.
С помощью товарищей я смогу решить свои проблемы.
Мне нужна помощь учителя.
Приложение 4
Класс: 8.
Повторительно-обобщающий урок по теме «КВАДРАТНЫЕ УРАВНЕНИЯ».
Цели:
- повторить, обобщить и закрепить знания, умения и навыки по теме;
- выяснить уровень знаний учащихся, умение применять знания;
- развивать культуру вычислительных навыков, логическое мышление;
- воспитывать ответственность, дисциплинированность;
- формировать ценные нравственные качества: доброту, отзывчивость, чуткость.
Оборудование:
- проектор;
- табличка-зашифровка;
- таблички «Пункт № 1», «Пункт № 2», Пункт № 3», «Пункт № 4»;
- тесты «Заполни пропуски», «Установи истинность», «Выбери ответ»;
- конверты с карточками-заданиями № 1 для сильных учеников и № 2 – для слабых;
- командировочные удостоверения.
Разминка.
а) Устный счёт (с помощью проектора).
- Вычислить дискриминант:
а) х2 + 5 х – 6 = 0; б) 2 х2 – 4 х + 7 = 0; в) у2 – 10 у + 25 = 0.
Ответы: а) 49; б) – 40; в) 0.
Дополнительный вопрос. Что можно сказать о корнях уравнений в каждом случае?
- Решить уравнение:
а) 5 х2 – 125 = 0; б) 3 х2 – 48 х = 0; в) 7 х2 + 14 = 0;
г) х2 + х – 6 = 0; д) х2 – 3 х – 18 = 0.
Ответы: а) –5; 5; б) 0; 16; в) нет корней; г) – 3; 2; д) – 3; 6.
Дополнительные вопросы:
- Какое уравнение называется квадратным? Приведите пример.
- Какое уравнение называется неполным квадратным уравнением. Приведите пример.
- Сформулируйте теорему Виета.
б) Расшифровка.
На доске прикреплена таблица:
| Дискриминант | О |
| Неполные | Р |
| 4,5 | А |
| Квадратные | Д |
| 24 | О |
| 16; 1 | Т |
| Приведённые | Б |
Учитель. Ребята, вы должны расшифровать данную таблицу. Я буду показывать вам табличку с вопросом. Вы должны записать ответ в левой стороне тетради в столбик и справа поставить букву, которая стоит в таблице против соответствующего ответа. Показываю таблицы с вопросами.
- Какие это уравнения: 2 х2 + 3 х – 7 = 0; 0,2 х2 – 10 х + 3,6 = 0 ?
- Как называется выражение b2 – 4 ac ?
- Какие это уравнения: х2 – 3 х +7 = 0; х2 – 10 х + 20 = 0 ?
- Какие это уравнения: 2 х2 + 4 х = 0; 5 х2 = 0; 12 х2 – 24 = 0 ?
- Чему равно произведение корней уравнения х2 – 10 х + 24 = 0 ?
- Чему равны корни уравнения х2 – 15 х – 16 = 0 ?
- Чему равна сумма корней уравнения 2 х2 – 9 х – 10 = 0 ?
Проверка результатов с помощью проектора: квадратные; дискриминант, приведённые; неполные; 24; 16, - 1; 4,5.
Ответ: ДОБРОТА.
Учитель. Мы сейчас, ребята, живём в очень трудное и сложное время. Но я думаю, что для вас доброта, чуткость, отзывчивость никогда не будут дефицитными качествами. Дарите людям добро, цените это качество в людях.
«Командировка»
Итак, разминка окончена. Сейчас вы отправляетесь в командировку в пункты № 1, № 2, № 3, № 4 со следующими заданиями: пункт № 1 – работа у доски, пункт № 2 – выполнить тест «Установи истинность», пункт № 3 – выполнить тест «Заполни пропуски», пункт № 4 – выполнить тест «Выбери ответ».
Если у вас останется время, вы сможете посетить пункты «Силён? Реши!», «Устал? Отдохни!»
Если вы окажетесь в одном пункте одновременно, будьте друг к другу чуткими. Но из командировки вы должны прибыть в час. Получите командировочное удостоверение. Итак, желаю удачи!
