Решение

Вид материала

Решение

Содержание Общая часть 1.2 Булева функция Суперпозиция функций 1.3 Математическая логика 1.4 Логика высказываний Пропозициональные формулы Теорема корректности. Теорема полноты. Способы задания графов Маршруты, циклы, связности. Свойства деревьев. Планарные графы. Парное сочетание (паросочетание) двудольных графов Теорема Холла (без доказательства)

Подобный материал:

• Найти частное решение линейного однородного дифференциального уравнения. Решение, 6.09kb.
• «Алгоритмизация и решение физических задач на эвм», 391.8kb.
• Навык 4 Думайте в духе «Выиграл выиграл», 91.19kb.
• Решение, 1036.71kb.
• Решение линейных уравнений Цель урока, 126.51kb.
• Совет депутатов г. Протвино решение от 25. 07. 2011 №241/38, 380.05kb.
• Решение страсбург, 1314.79kb.
• Герция Виталия Михайловича, Садоводческого некоммерческого партнерства «Речник» иОрлова, 141.35kb.
• Первая Вторая половина ХIХ начало ХХ вв. Право и жизнь в адыгском обществе, 3427.05kb.
• Республика мордовия рузаевский муниципальный район совет депутатов городского поселения, 19.08kb.

Содержание


Введение………………………………………………………………………………………………………………………. 3

1. Общая часть………………………………………………………………………………………………. 4
   
   0. Множества и операции над ними…………………………………………………………………… 4
      
   1. Булева функция………………………………………………………………………………………………………. 5
      
   2. Математическая логика…………………………………………………………………………………….. 6
      
   3. Логика высказываний…………………………………………………………………………………………… 7
      
   4. Графы……………………………………………………………………………………………………………………………. 8
      
2. Задачи………………………………………………………………………………………………………………. 12
   
3. Решение............................................................................................................. 14
   
4. Заключение………………………………………………………………………………………………………………..
   

Литература……………………………………………………………………………………………………………………………


Введение


Общество 21в. – общество информационное. Центр тяжести в решении задач переместился от задач вычислительной математики к задачам на дискретных структурах. Математика нужна не как метод расчета, а как метод мышлению средство формирования и организации…

В курсе изучаются фундаментальные понятия, лежащие в основе математической кибернетики и таких разделов математики как алгебра, теория графов, математическая логика. Хотя данные разделы и являются отдельными математическими теориями, они не только используют методы друг друга, но и тесно связаны между собой. Все их можно объединить условным названием ``дискретная математика''. Этот термин характеризует конструктивный характер теории, алгоритмические, комбинаторные методы. Задачи дискретной математики, как правило, тесно связаны с компьютерными проблемами, естественно выражаются в виде различных алгоритмов.

Историческая справка

Дискретная математика, по-существу, стала активно развиваться с начала XX века, когда стали изучаться возможности формализации математики и были получены фундаментальные результаты в области математической логики. Это результаты Поста, Клини и, особенно, Гёделя. Теорема неполноты Гёделя имеет мировоззренческое значение – она показывает ограниченность формальных методов построения математической теории.

В основе дискретной математики 4 раздела:

1. Язык дискретной математики;
   
2. Логические функции и автоматы;
   
3. Теория алгоритмов;
   
4. Графы и дискретные экстремальные задачи.
   

Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.

Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно сложные задачи (задачи перебора) и неразрешимые задачи.

1. Общая часть
   

0. Множества и операции над ними
   

Одно из основных понятий математики – множество.

Определение:

Множеством называется совокупность, набор предметов, объектов или элементов.

Множество обозначают: M,N …..

m₁, m₂, m_n – элементы множества.

Символика

A  M – принадлежность элемента к множеству;

А  М – непринадлежность элемента к множеству.

Примеры числовых множеств:

1,2,3,… множество натуральных чисел N;

…,-2,-1,0,1,2,… - множество целых чисел Z.

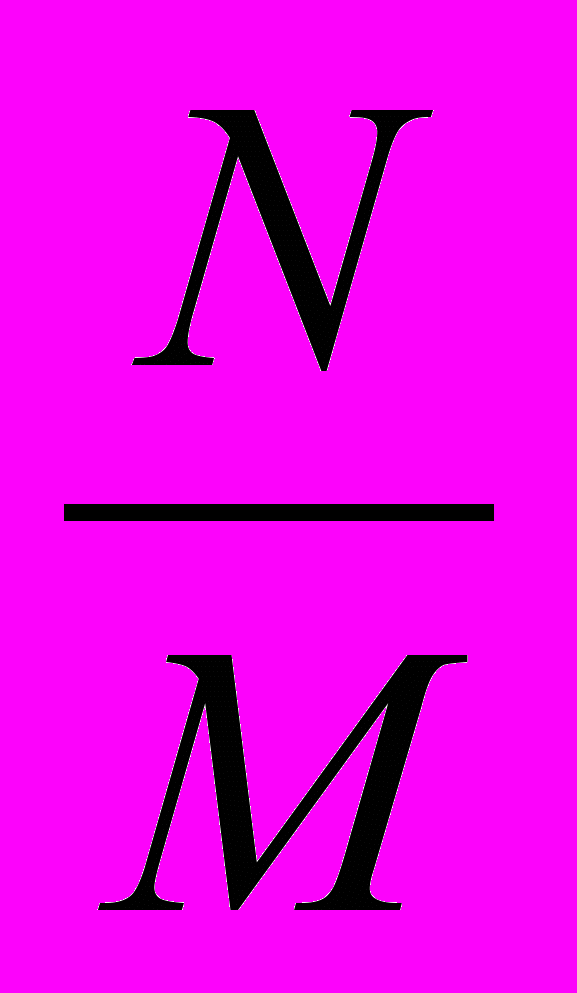множество рациональных чисел а.

I – множество иррациональных чисел.

R – множество действительных чисел.

K – множество комплексных чисел.

Множество А называется подмножеством В, если всякий элемент А является элементом В.

А  В – А подмножество В (нестрогое включение)

Множества А и В равны, если их элементы совпадают.

A = B

Если А  В и А  В то А  В (строгое включение).

Множества бывают конечные и бесконечные.

|М| - мощность множества (число его элементов).

Конечное множество имеет конечное количество элементов.

Пустое множество не содержит элементов: M = .

Существует 5 операций над множествами:

1. объединение (сумма) множеств А и В представляет собой множества состоящие из элементов, принадлежащих хотя бы одному из множеств А и В. Если какой-нибудь элемент входит в оба множества, то в объединении этих множеств он включается только 1 раз
   
2. пересечение (умножение) множеств А и В – это множество, которое состоит из элементов принадлежащих каждому из множеств.
   
3. разность. Порядок множеств существенный. В отличии от первых двух операций разность строго двулична и не камутативна.
   
4. симметрическая разность множеств А и В представляет собой множество, состоящее из элементов, принадлежащих в точности одному из множеств А и в.
   
5. дополнения. Если А 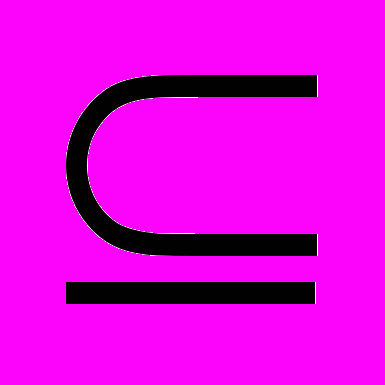Е, то дополнения (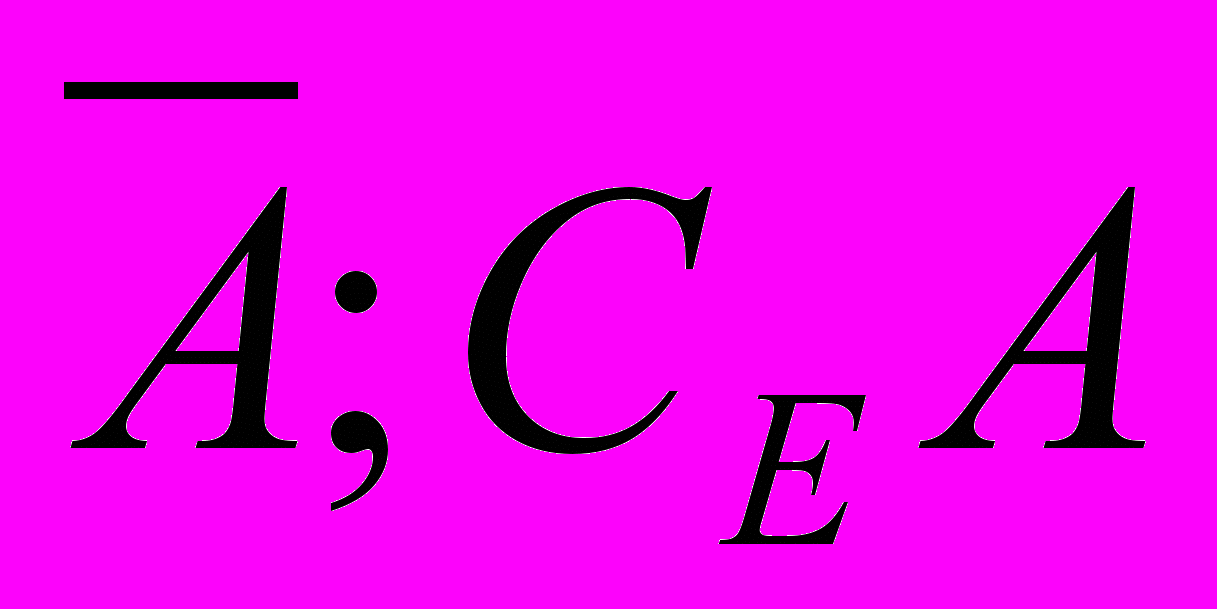); относительно Е определяется так: 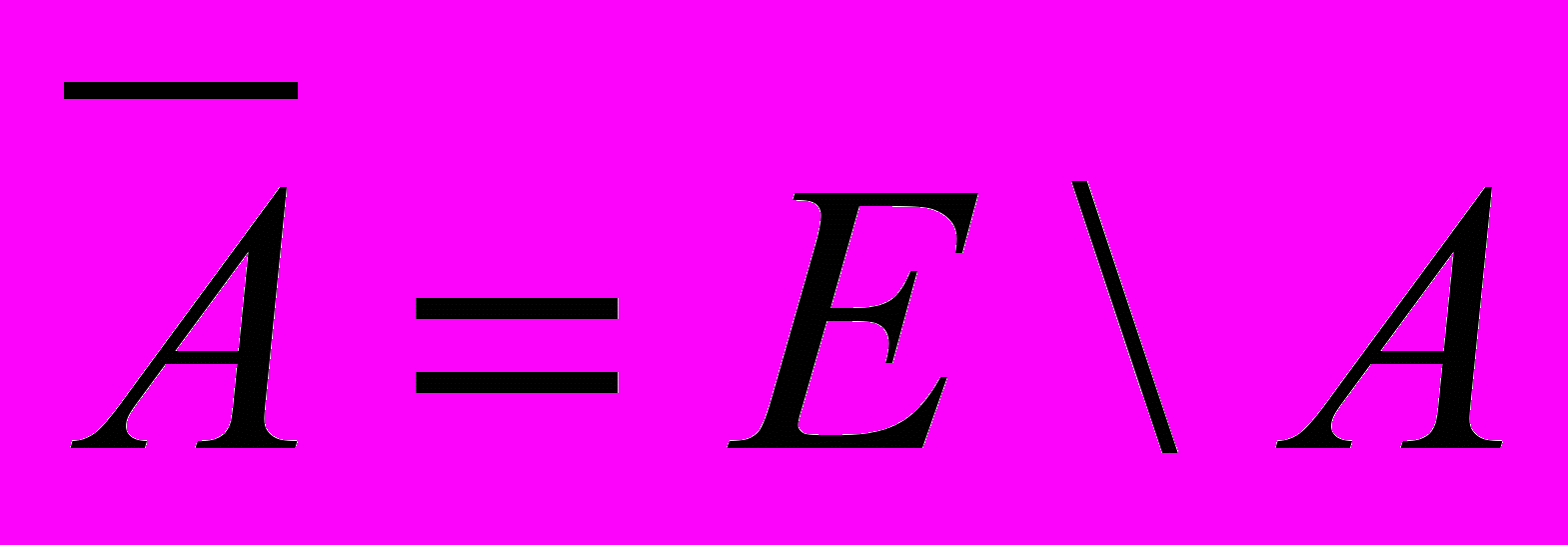т.е. это множество трех элементов, которые не принадлежат множеству А, а принадлежат множеству С.
   

1.2 Булева функция




Понятие булевой функции

Определение (Булева функция). Булевой функцией от n аргументов называется функция f из n-ой степени множества { 0, 1 } в множество { 0, 1 }. Иначе говоря, булева функция – это функция, и аргументы и значение

которой принадлежит множеству { 0, 1 }. Множество { 0, 1 } мы будем в дальнейшем обозначать через B. Булеву функцию от n аргументов можно рассматривать как n-местную алгебраическую операцию на множестве B. При этом алгебра , где  – множество всевозможных булевых функций называется алгеброй логики.

Определение (Фиктивные и существенные переменные). Переменная x_i называется фиктивной (несущественной) переменной функции f(x₁,···,x_n), если

f(x₁,···,x_i-1,0,x_i+1,···,x_n) = f(x₁,···,x_i-1,1,x_i+1,···,x_n)

для любых значений x₁,···,x_i-1,x_i+1,···,x_n. Иначе переменная x_i называется существенной. Функций от двух аргументов шестнадцать. Наиболее употребимые из этих функций только те, которые существенно зависят от обеих переменных.Эти функции записываются как бинарные операции в инфиксной нотации. x₁ & x₂ называется конъюнкцией, x₁  x₂ – дизъюнкцией, x₁  x₂ – импликацией, x₁  x₂ – эквивалентностью, x₁  x₂ – суммой по модулю 2, x₁ | x₂ – штрихом Шеффера. Значения 0 и 1 часто интерпретируют как ``ложь'' и ``истину''. Тогда понятным становится название функции ``отрицание'' – она меняет ``ложь'' на ``истину'', а ``истину'' на ``ложь''. Отрицание читается как ``не''. Конъюнкция читается обычно как ``и'' – действительно, конъюнкция равна 1 тогда и только тогда, когда равны 1 и первая и вторая переменная.<sup>*</sup> Кроме x<sub>1</sub>& x<sub>2</sub> часто используют обозначение x<sub>1</sub>  x<sub>2</sub> или x<sub>1</sub> · x<sub>2</sub> или x<sub>1</sub>x<sub>2</sub> или min(x<sub>1</sub>,x<sub>2</sub>). Дизъюнкция читается ``или'' – дизъюнкция равна 1 тогда и только тогда, когда равны 1 первая или вторая переменная.^* Импликация выражает факт, что из x₁ следует x₂.^* Импликацию часто также обозначают x₁  x₂.

Суперпозиция функций

Определение (Суперпозиция функций). Суперпозицией булевых функций f₀ и f₁,...,f_n называется функция f(x₁,...,x_m) = f₀(g₁(x₁,...,x_m),...,g_k(x₁,...,x_m)), где каждая из функций g_i(x₁, ...,x_m) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f₁,...,f_n.

3 Двойственные функции

Симметрия элементов 0 и 1 в множестве B приводит к понятию двойственности.

Определение (Двойственная функция). Функция g(x₁,...,x_n) = ¬f(¬x₁,...,¬x_n) называется двойственной функцией к функции f и обозначается f^*