Решение
| Вид материала | Решение |
- Найти частное решение линейного однородного дифференциального уравнения. Решение, 6.09kb.
- «Алгоритмизация и решение физических задач на эвм», 391.8kb.
- Навык 4 Думайте в духе «Выиграл выиграл», 91.19kb.
- Решение, 1036.71kb.
- Решение линейных уравнений Цель урока, 126.51kb.
- Совет депутатов г. Протвино решение от 25. 07. 2011 №241/38, 380.05kb.
- Решение страсбург, 1314.79kb.
- Герция Виталия Михайловича, Садоводческого некоммерческого партнерства «Речник» иОрлова, 141.35kb.
- Первая Вторая половина ХIХ начало ХХ вв. Право и жизнь в адыгском обществе, 3427.05kb.
- Республика мордовия рузаевский муниципальный район совет депутатов городского поселения, 19.08kb.
={(a,a),(a,c),(a,g),(a,i),(b,a),(b,c),(b,e),(b,g),(b,i),(c,a),(c,c),(c,g),(c,i),(d,a),(d,c), (d,e),(d,g),(d,i),(e,a),(e,c),(e,e),(e,g),(e,i)} Задача 4
Для конечного множества А = {1,2,3,4,5,6,7,8,9,10} составить матрицу отношения, установить, какими свойствами обладает отношение, установить является ли это отношение отношением эквивалентности или порядка(какого порядка).
Отношение: неравенство.
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 6 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Данная матрица обладает следующими свойствами:
- антирефлексивность
- симметричность
- транзитивность
; 
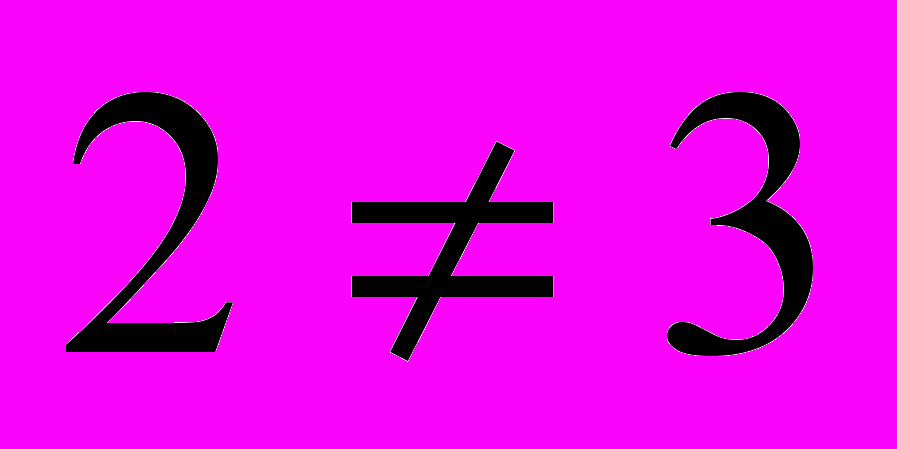; значит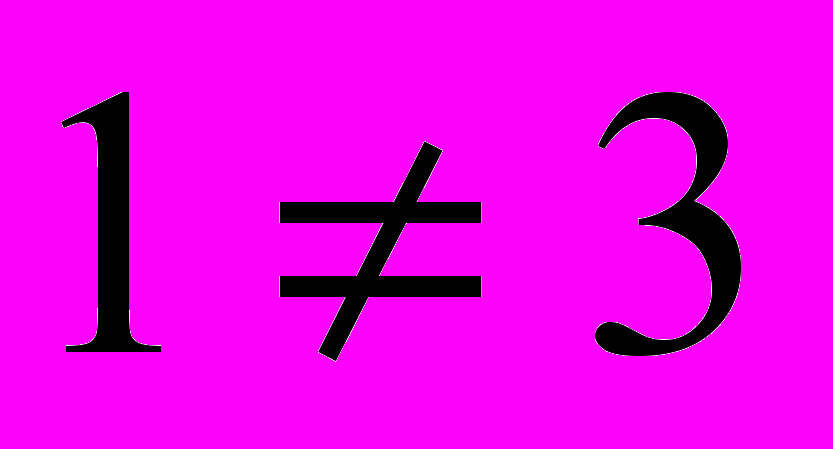 
Так же матрица неэквивалентна, так как не обладает свойством рефлексивности, но является отношением строгого порядка, так как обладает свойством антирафлексивности.
Задача 5Дано множество V векторов одинаковой длины. Записать проекции векторов с V на i-тую ось.
V = {(a,d,s,o),(b,d,s,o),(c,d,d,f)}
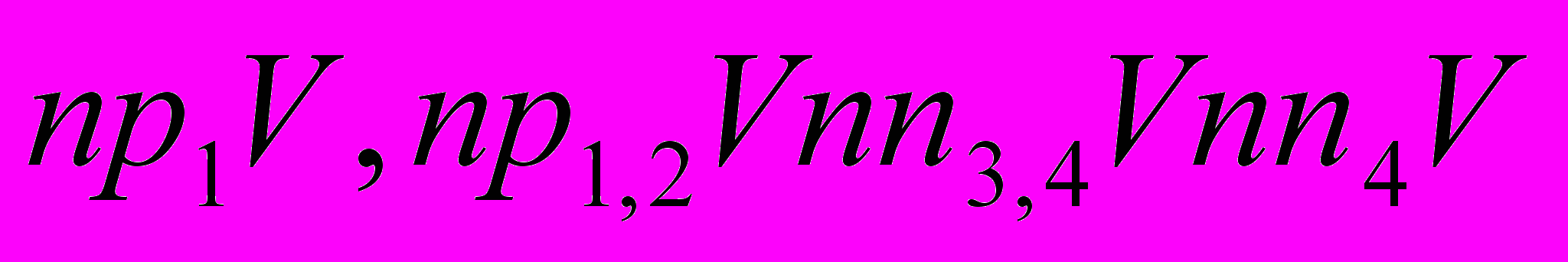
Задача 6
Даны три логических высказывания: А, В, и С. Построить таблицу истинности для логической операции:
Таблица истинности выражения
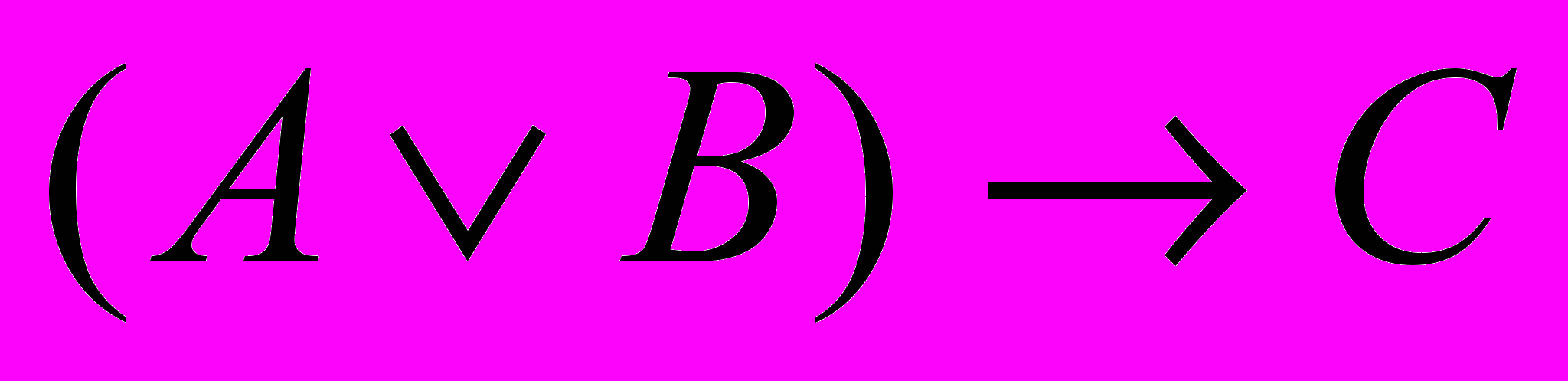будет состоять из восьми строк и пяти столбцов:| № | А | В | С |  | |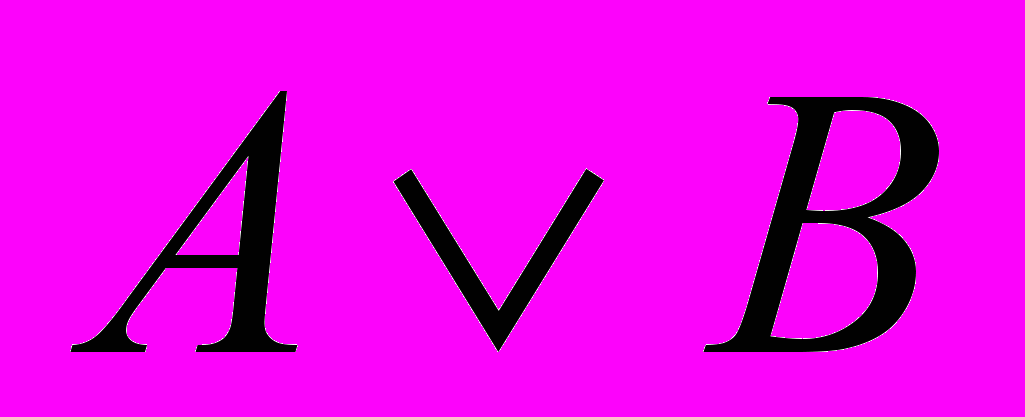
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 1 | 1 |
| 6 | 1 | 0 | 1 | 1 | 1 |
| 7 | 1 | 1 | 0 | 1 | 1 |
| 8 | 1 | 1 | 1 | 1 | 1 |
Задача 7
Выяснить, является ли следующая формула тавтологией:
| Х | Y |  | |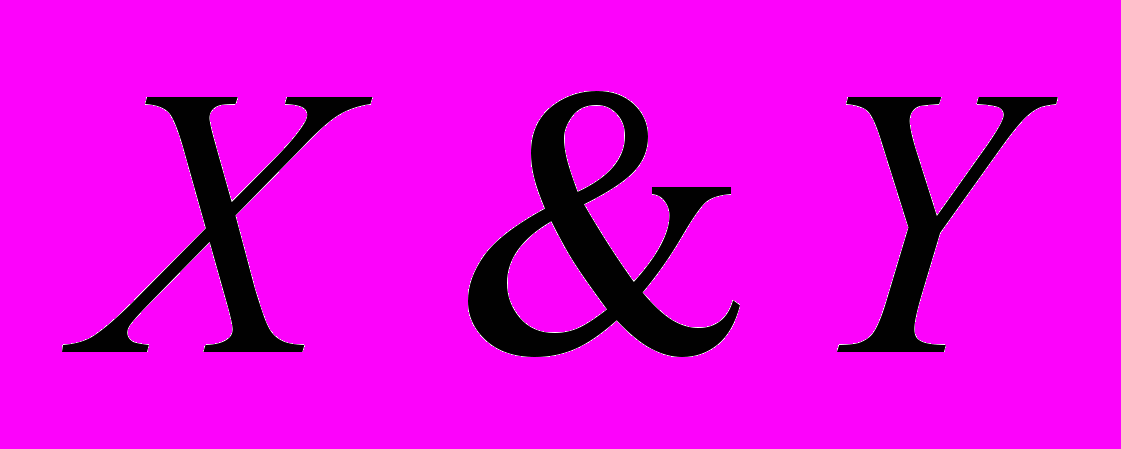
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Так как в последнем столбце нет ни одного нуля, данная формула является тавтологией.
Задача 8
Выяснить любым способом, будут ли данные формулы равносильным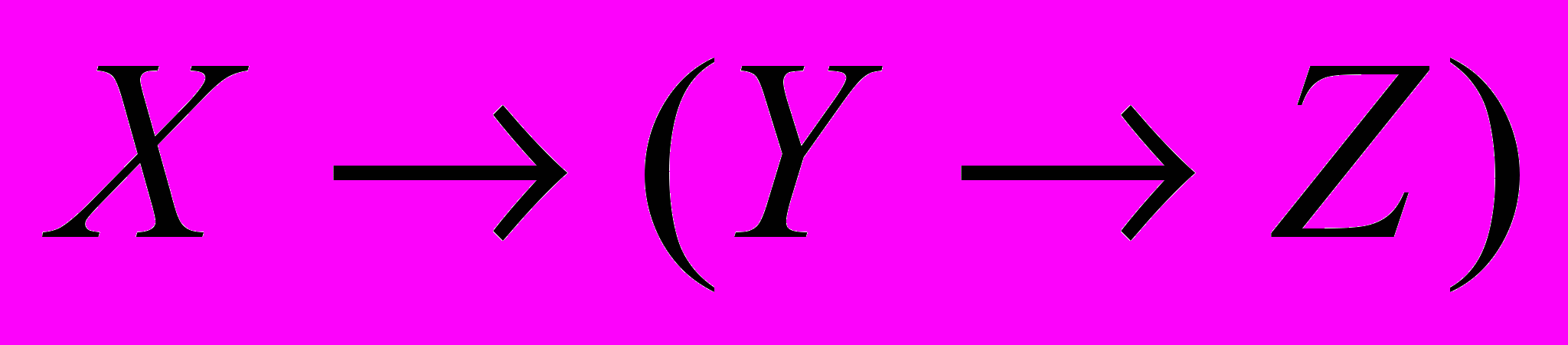и:
и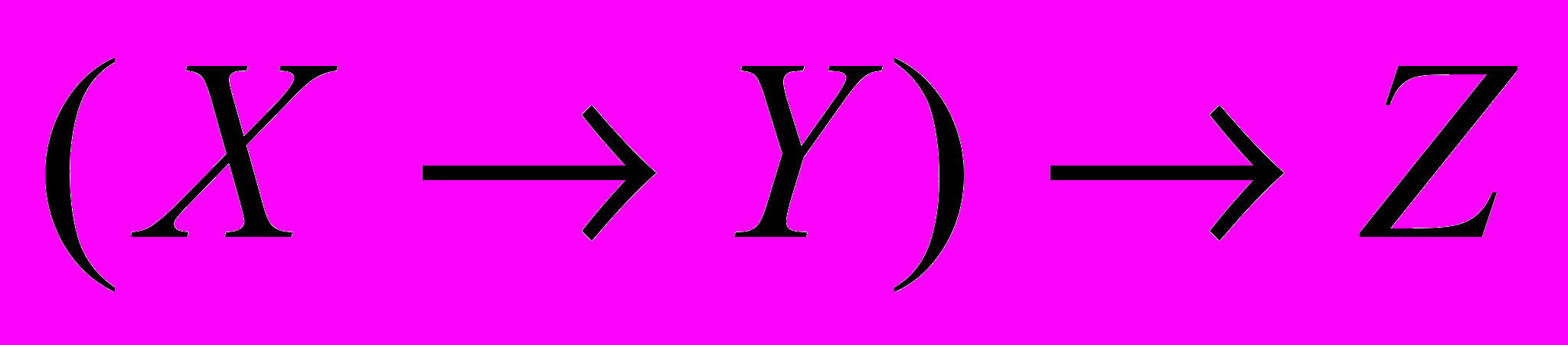 
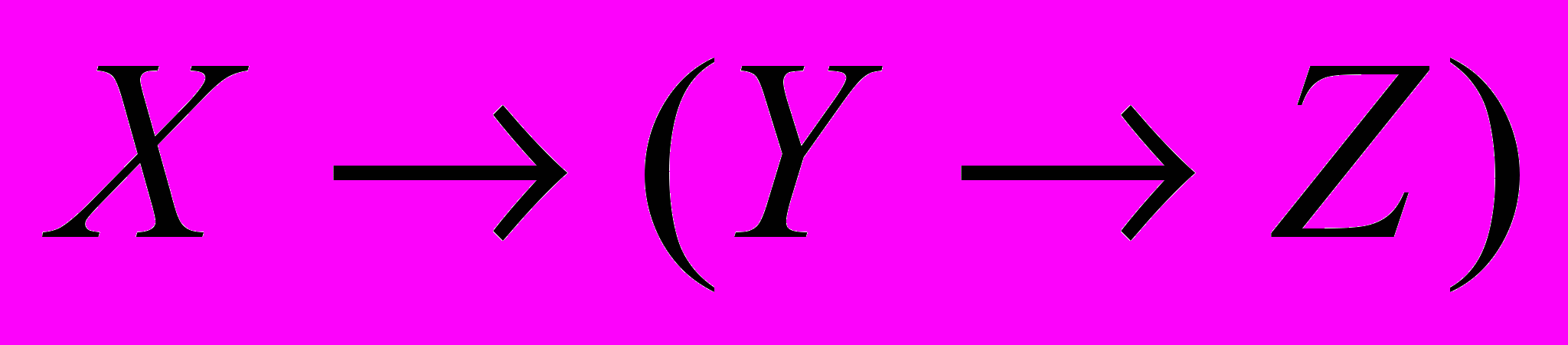
| X | Y | Z |  | |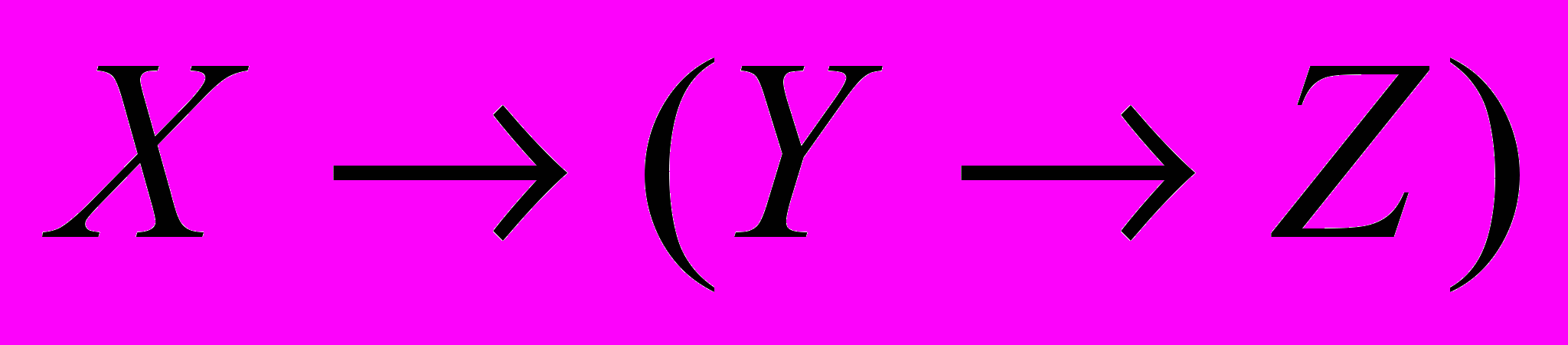
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
-
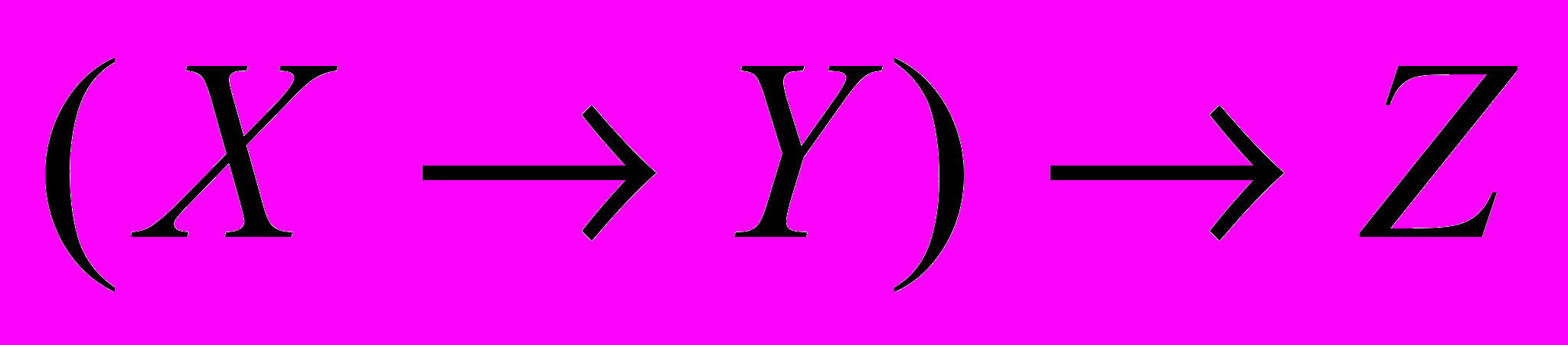
X
Y
Z
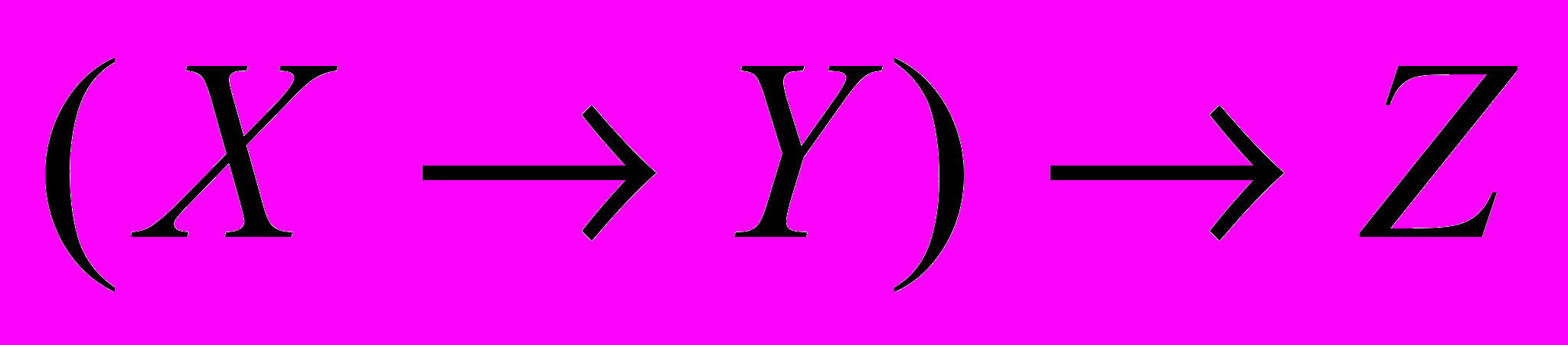
0
0
0
1
0
0
0
1
1
1
0
1
0
1
0
0
1
1
1
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
0
1
1
1
1
1