План исследования 8 Современное состояние проблемы 9 Описание эксперимента 10 Метод текущего Парето [7] 10 Метод moga [1] 11

Вид материала

Подобный материал:

1 2 3 4 5 6 7

Эксперимент “10,50,50”

Шаг	Размер вычисленного Парето	Вычислено решений общего Парето	средние ошибки	максимальные ошибки
РГ -> МТП -> ММД -> КДЦ	36	7	[1770; 1140; 2]	[8400; 1140; 3]
МТП -> РГ-> ММД -> КДЦ	37	6	[3062; 1140; 1]	[17700; 1140; 1]
РГ-> ММД -> КДЦ	41	8	[3487; 1140; 1]	[16100; 1140; 2]
МТП -> ММД -> КДЦ	39	9	[3475; 3300; 1]	[15700; 5460; 1]
МП -> ММД -> КДЦ	40	9	[2653; 5460; 1]	[17500; 5460; 1]

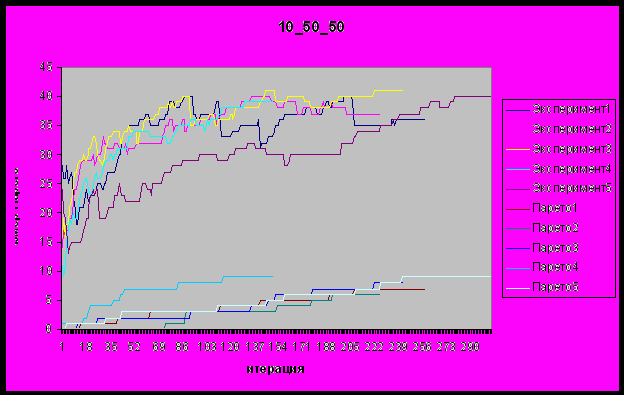
Ниже приведены данные для первых 500 поколений с размером поколения 100:

Шаг	Размер вычисленного Парето	Вычислено решений общего Парето	средние ошибки	максимальные ошибки
РГ -> МТП -> ММД -> КДЦ	32	9	[1847; 1020; 1]	[16000; 1740; 1]
МТП -> РГ-> ММД -> КДЦ	36	8	[3192; 0; 0]	[13200; 0; 0]
РГ-> ММД -> КДЦ	39	15	[4275; 870; 1]	[37200; 1440; 1]
МТП -> ММД -> КДЦ	36	10	[1080; 0; 0]	[4600; 0; 0]
МП -> ММД -> КДЦ	32	6	[3030; 0; 0]	[13700; 0; 0]

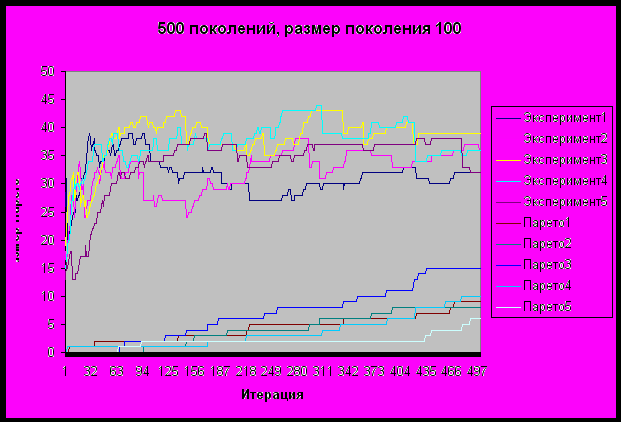
Выводы из результатов

Средние отклонения от общего множества Парето приведены с учетом только тех вариантов, которые не попали в общее множество Парето.

Как видно из приведенных выше результатов, существенных преимуществ в использовании того или иного подхода не наблюдается. Явное превосходство того или иного метода ранжирования над остальными носит скорее случайный характер. Однако можно выделить определенные закономерности.

Исходя из средних отклонений от Парето и графиков роста текущего Парето видно, можно заключить, что Метод Текущего Парето хорошо работает на тех итерациях, когда множество оценок уже сосредоточено вблизи истинного Парето. То есть в середине процесса поиска.

Совместное использование МТП и РГ позволяет уменьшить среднее отклонение результата от истинного Парето по каждому из параметров. Однако оно не дает хорошей сходимости к множеству Парето, поэтому ее следует использовать на последних итерациях поиска для выравнивания результата.

Метод Парето, по сути, осуществляет поиск по так называемому методу «Монте Карло. Уже на средних размерностях подход ненадежен. Это видно из нестабильности его поведения в разных сценариях и максимального среди приведенных средних отклонений от общего Парето. Дополнительно следует заметить, что его текущее Парето уступает по размерам ТП остальных методов.

Из сказанного выше следует рекомендация по построению алгоритма поиска расписания:

На начальных этапах использовать цепь РГ -> ММД -> КДЦ для оценки множества истинного Парето небольшим количеством точек.
В середине поиска – МТП -> ММД -> КДЦ. Это позволит увеличить объем результата и сузить поколение
В конце – РГ -> МТП -> ММД -> КДЦ с целью уменьшить среднее расстояние до истинного Парето.

Заключение

В исследовании рассматривается нетривиальная постановка задачи поиска расписаний. Она отличается от традиционных возможностью одновременного учета сложных зависимостей между задачами и ограничений на время перемещения инженеров. Описанные механизмы обладают достаточной гибкостью, что позволяет легко вводить новые критерии, типы зависимостей и прочие ограничения на время выполнения задач.

В рамках данной работы предложено расширение стандартного подхода составления расписаний, предназначенное для организации алгоритмов адаптивного поиска, предложены методы его оптимизации, проанализирована зависимость сложности алгоритма составления расписания от параметров задачи. Предложены и проанализированы комбинации различных способов ранжирования поколений генетического алгоритма поиска.

Результаты экспериментальной проверки показали, что задача обладает хорошей масштабируемостью: около 90% всего времени выполнения поиска уходит на независимые друг от друга операции составления расписаний по ключу, а так же на их анализ. И только 10% тратится на организацию поиска. Это означает, что достаточно двух 8-процессорных серверных машин средней мощности, чтобы ускорить поиск в 8-9 раз. Например, для размерности 1000 задач, 50 работников, 100 локаций время генерации одного расписания составляет 7 секунд. При размере поколения 500 время обработки одного поколения (обработка 100 новых задач) в общей сложности составит порядка 15 минут. Или порядка 2 минут в высокопараллельной системе. Что даст возможность обработать 500 поколений - среднее число поколений, необходимых для достижения неизменности множества оценок на меньших размерностях - за 16 часов.

Далее в рамках этой темы предполагается более глубокое исследование и оптимизация предложенных и новых алгоритмов поиска. Поиск в практике управления персоналом и исследование более сложных зависимостей между задачами. Анализ возможностей и перспектив применения методов сужения множества Парето, в том числе Теории Важности Критериев (ТВК). Исследование применимости к поиску расписаний подходов нечеткой логики.

Так же планируется попытка внедрения описанного прототипа в систему OSS

Список литературы

Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization. Carlos M. Fonsecay and Peter J. Flemingz. Dept. Automatic Control and Systems Eng. University of Sheeld. Sheeld S1 4DU, U.K.
Комбинаторные алгоритмы: теория и практика. Рейнгольд Э., Нивергельт Ю., Део Н. год издания - 1980, 476с
Computer and job-shop scheduling theory (E.G. Coffman Jr). John Willey & Sons, 1976
http ://tmforum .org
Evtushenko Yu.G., Potapov М.А. Deterministic global optimization // Algorithms Continuous

Optimizat. State Art. Kluver: Acad. Publ., 1994. P. 481-500.

Евтушенко Ю.Г., Потапов М.А. Методы численного решения многокритериальных задач // Доклады АН, 1986, том 291 №1. С. 25-29.
Евтушенко Ю. Г., Потапов М. А. Численные методы решения многокритериальных задач // Кибернетика и вычислит, техника. 1987. Вып. 3. М.: Наука, С. 209 - 218.
Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. Москва: Наука. 1982.
Решение задачи локальной оптимизации расписания при управлении персоналом. Васильев А.В. Материалы XXXVII международной конференции дискуссионного научного клуба “Информационные технологии в науке, образовании, телекоммуникации и бизнесе”. Приложение к журналу ”Открытое образование”. 2010 г.
Многокритериальный выбор решений для задачи управления персоналом. Потапов М.А., Некрылов Д.А., Кутафин А.А. Материалы XXXVII международной конференции дискуссионного научного клуба “Информационные технологии в науке, образовании, телекоммуникации и бизнесе”. Приложение к журналу ”Открытое образование”. 2010 г.
Генетические Алгоритмы (Аналитический обзор). Шатохин Д.С.
Matthew Wall. Galib 2.45 Genetic Algorithms Library Documentation. http ://lancet .mit .edu /ga /
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. Перевод с английского Е.В. Левнера и М.А. Фрумкина под ред. А.А. Фридмана. М.: Мир, 1982
David Beasley. Evolutionary Algorithms – Frequently Asked Questions. //comp.ai.genetic newsgroup, 2001
Методы многокритериальной целочисленной оптимизации, основанные на аппроксимации границы Парето. Поспелов А.И. диссертация на соискание ученой степени кандидата физико-математических наук, Москва 2010
GruberP.M., Kenderov P. Approximation of convex bodies by polytopes // Rendiconti Circolo mat. Palermo. Ser.II. 1982. T. 31. No 2. P. 195-225.
Н. Б. Брусникина, Г. К. Каменев, “О сложности и методах полиэдральной аппроксимации выпуклых тел с частично гладкой границей”, Ж. вычисл. матем. и матем. физ., 45:9 (2005),1555–1565
Fleming, P. J. (1985). Computer aided design ofregulators using multiobjective optimization. In Proc. 5th IFAC Workshop on Control Applica-tions of Nonlinear Programming and Optimiza-tion, pp. 47{52, Capri. Pergamon Press.
Schaer, J. D. (1985). Multiple objective optimization with vector evaluated genetic algorithms. In Grefenstette, J. J., editor, Proc. First Int. Conf. on Genetic Algorithms, pp. 93{100. Lawrence Erlbaum.

Blog

План исследования 8 Современное состояние проблемы 9 Описание эксперимента 10 Метод текущего Парето [7] 10 Метод moga [1] 11

Эксперимент “10,50,50”

Выводы из результатов

Заключение