Geum.ru

План исследования 8 Современное состояние проблемы 9 Описание эксперимента 10 Метод текущего Парето [7] 10 Метод moga [1] 11

Вид материалаДиссертация
Современное состояние проблемы
Описание эксперимента
Метод MOGA [1]
Подобный материал:
1   2   3   4   5   6   7

Современное состояние проблемы


В стандарте управления расписаниями вводятя два шага поисковой оптимизации: долгосрочная и краткосрочная. Работающих с данными последующих нескольких недель и следующего дня соответственно. Исходя из оценки 4 задачи на работника в день и пятиста работников, при полном переборе последняя требует рассмотрения более, чем различных вариантов расписаний (приведенная оценка дает точный результат если каждый работник должен иметь ровно 4 задачи в день, при этом опция перераспределения свободного времени между задачами не рассматривается).

Сейчас широко развивается теория и практика применения алгоритмов адаптивного поиска, в частности генетических алгоритмов, для решения задач большой размерности. На каждом шаге такого алгоритма формируется “поколение” лучших из найденных вариантов, и в некоторые из рассматриваемых решений вносятся случайные изменения для образования следующего поколения. [11,12]

После получения расширенного набора вариантов в результате случайных преобразований поколения мы должны исключить из рассмотрения некоторые из найденных возможных решений. Следует исключать именно те решения, которые уводят поиск в сторону от требуемого результата, и поэтому необходимо каким-то образом сравнить, насколько одно из них ближе к результату, чем другое. Важно заметить, что многокритериальная постановка не позволяет ввести явную функцию приспособленности при отсутствии точной информации о геометрических свойствах множества Парето. Или его подмножества, интересного ЛПР. Это обосновывается тем, что если функция приспособленности не постоянна на всем наборе искомых оценок, ее применение приведет к неоправданному исключению из рассмотрения одинаково удовлетворительных опций.

Для обеспечения работоспособности поисковых алгоритмов необходимо ввести некоторый аналог экстремума.

Для этого в работе используются два метода: текущего Парето (МТП) и MOGA. Они позволяют упорядочить текущее поколение генетического алгоритма и таким образом обеспечивают его сходимость.

Описание эксперимента

Метод текущего Парето [7]


Суть МТП состоит в выделении в текущем поколении множества недоминируемых вариантов. Это множество будем называть текущим множеством Парето. Оно служит для сравнения друг с другом оставшейся части геномов поколения и определения, какие из них следует использовать в следующей итерации, а какие нужно отбросить. Принцип построения ТП удобно отобразить на диаграме



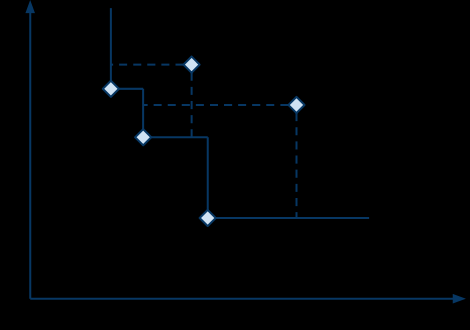
Пусть поколение состоит из пяти элементов: p1-p5. Требуется минимизировать два критерия: y1 и y2. Текущее Парето, очевидно, будет состоять из векторов p1, p2 и p3. Вводится понятие расстояния до текущего Парето: ,

где ppar - точка Текущего Парето.

Согласно исследованиям Ю.Г. Евтушенко и М.А. Потапова, сортировка по расстоянию до текущего Парето при выборе набора лучших геномов для генерации следующего поколения и худших геномов, исключаемых из рассмотрения, ускоряет сходимость поиска к истинному Парето. В данной работе сделано обобщение МТП на дискретный случай.

Сложность алгоритма обработки поколения при применении этого метода в худшем случае будет равна



Где

N - размер поколения

Np - количество недоминируемых вариантов в поколении

c - количество критериев

Оценка реализуется тогда, когда первые (N-Np) геномов поколения попарно не доминируют друг друга и доминируются только последним.

Метод MOGA [1]


Метод MOGA так же служит для ранжирования геномов текущего поколения. Как уже упоминалось выше, он включает в себя два этапа:

1. Упорядочение элементов по количеству доминирующих вариантов

2. Упорядочение элементов по количеству выполненных целей

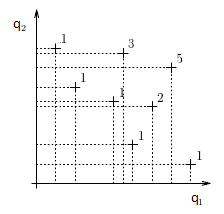
На первом этапе для каждого элемента находится число геномов того же поколения, которые его доминируют. Исходя из этого числа геному присваивается ранг r по правилу r=n+1, где n - число доминирующих геномов. Диаграма 2 иллюстрирует приведенное правило.

Традиционно используются три способа обработки значений рангов:
    1. поколение сортируется в соответствии с рангом
    2. геномам присваиваются значения приспособленности линейно пропорционально рангу.
    3. средние значения функции приспособленности индивидов одного ранга делаются пропорциональными рангу. Таким образом, геномы одного ранга будут обрабатываться с одинаковой частотой.

Очевидно варианты a и b дают эквивалентный результат. Варианты b и c эффективны при совместном применении MOGA и какого-либо другого метода, основанного на функции предпочтительности.


Ключевым моментов второго этапа является понятие цели. Цель, обозначим ее g, представляет собой векторную оценку в том же пространстве критериев Q. Это может быть оценка уже имеющегося решения, которое мы хотим улучшить. Либо точка за пределами множества допустимых решений, варианты, доминируемые которой, нас не интересуют. Для генома p введем понятие количества выполненных целей G(p).

G(p) = (Q - размерность пространства критериев)

Назовем геном удовлетворительным, если G(p) = Q.

Пусть имеются два варианта: p1, p2 и цель g. Будем считать вариант p1 предпочтительным по отношению к p2 если G(p1) > G(p2).

Таким образом, мы получим правило упорядочения вариантов, дающее сходимость поиска

-к подмножеству множества Парето, состоящему только из удовлетворительных опций, если цель достижима

-к вариантам, доминирующим цель по максимально возможному числу критериев, если цель недостижима.

Вычислительная сложность обоих этапов, очевидно, пропорциональна N2.