План исследования 8 Современное состояние проблемы 9 Описание эксперимента 10 Метод текущего Парето [7] 10 Метод moga [1] 11

Вид материала

Диссертация

Содержание Комбинирование методов оценки Ограничения на время выполнения задач

Подобный материал:

• Практических: 0 Лабораторных:, 21.53kb.
• Программа исследования, 416.21kb.
• Правила составления социологической анкеты. Опрос экспертов как метод социологического, 15.89kb.
• Методика это более узкое понятие. Например, в экспериментальном методе исследования, 21.98kb.
• 1 Метод статистического моделирования, 167.94kb.
• Темы курсовых работ по курсу «Программирование» для студентов группы биб-11-1 (2011-2012, 85.51kb.
• Методика исследования 4 Штатно-номенклатурный метод 4 Метод расчета коэффициентов насыщенности, 831.9kb.
• Расшифровка : Наука в целом (информационные технологии 004), 79.71kb.
• Урока литературы в 9 классе на тему: «Древнерусская литература и современность. Золотое, 43.48kb.
• План Экспериментальный метод в науке и его трансформация в метод познавательной деятельности, 192.2kb.

Комбинирование методов оценки

Приведенные выше подходы призваны исключить некоторый элемент случайности направления поиска и обеспечить сходимость поколения к требуемому результату. На диаграмах 1 и 2 изображены участки множества Парето, которые скорее всего будут интересны ЛПР в зависимости от положения цели.





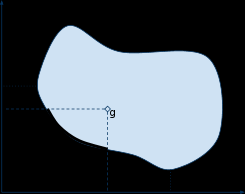
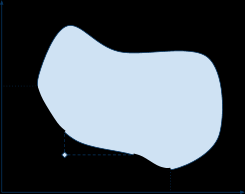
Диаграма 1 Диаграма2

Для любого из приведенных выше методов сортировки геномов по предпочтительности найдется такая пара оценок, которые будут несравнимы. Смысл применения нескольких методов последовательно - ввести дополнительный порядок для решений, признанных равными предыдущим методом. В попытке улучшить сходимость алгоритма. При этом если метод A отличается от B только порядком несравнимых по B решений, комбинирование A и B не имеет смысла. В противном случае комбинирование A и B требует дополнительного исследования, так как изменение способа применения подходов повлияет на поведение процесса поиска.

В данной работе будет произведен анализ совместного использования различных цепочек из пяти перечисленных ниже механизмов:

1. Ранжирования геномов (РГ)

2. Сравнения по количеству достигнутых целей (КДЦ)

3. Текущего Парето (МТП)

4. Выделения Парето (МП)

5. Минимакса дистанции (ММД)


Пункты 4 и 5 ранее не упоминались. Суть подхода 4 состоит в предпочтении точек текущего Парето точкам, которые в него не входят. Подход пункта 5 предназначен для предотвращения сходимости поиска к одной точке. Он подразумевает сортировку поколения по возрастанию минимальной удаленности векторной оценки от ближайшей точки того же поколения. В большинстве многокритериальных задач значения критериев попарно несравнимы, в качестве метрики в пространстве оценок чаще всего используется норма ∞. Ее применение логически обосновано и затраты на ее вычисление достаточно малы. Исследование способов обеспечения равномерного покрытия пространства результатов выходит за рамки данной работы. Поэтому именно норма ∞ была выбрана для реализации ММД. Само пространство при этом нормируется и приводится к отрезку [0,1]. Что позволяет работать с разными шкалами для каждого из критериев.

Механизм ММД использует скалярную функцию приспособленности, которая вычисляется следующим образом:

F =

где 1 < i,j < G (G - размер поколения)

p_i[k] - k-я компонента векторной оценки p_i

P_k=max0(p[k]) - min0(p[k])


Обратим внимание на способ комбинирования произвольных механизмов A и B для упорядочения одного поколения. Комбинацию, в которой механизм A применяется первым, а B - вторым будем обозначать (A,B). Предлагаемый способ их комбинирования заключается в следующем. Если A определил, что p1 более (или менее) предпочтителен, чем p2, способ B не должен менять это соотношение. Если же подход A признал p1 и p2 одинаково предпочтительными (или несравнимыми), предпочтение должно определяться на основе B. Аналогично для оставшихся подходов в цепочке.

В работе исследованы следующие комбинации вышеупомянутых подходов

• (РГ, МТП, ММД, КДЦ)
  
• (МТП, РГ, ММД, КДЦ)
  
• (РГ, ММД, КДЦ)
  
• (МТП, ММД, КДЦ)
  
• (МП, ММД, КДЦ)
  

И произведено сравнение сравнение эффективности применения этих цепочек.

Эксперимент спроектирован таким образом из следующих соображений:

• В первую очередь должны применяться механизмы, ускоряющие сходимость поиска к множеству Парето. Иначе результат их работы будет частично или полностью теряться
  
• КДЦ предназначен для обеспечения сходимости поиска в область удовлетворительных решений. Остальные механизмы никак не влияют на относительную предпочтительность элементов текущего Парето, поэтому применение КДЦ для ТП может производиться на любом этапе. Однако его применение для остальной части поколения будет сужать рассредоточенность последнего, не давая при этом какого-либо ускорения сходимости поиска к множеству Парето.
  

Все множество Парето может оказаться слишком большим для обработки в рамках поколения, и хранения. Так же ЛПР не сможет принять решение, выбирая из большого числа опций. Поэтому имеет смысл ставить цель найти подмножество множества Парето, равномерно распределенное (в смысле какой-либо метрики) по истинному МП. Это позволит оценить возможности системы в целом и сузить область поиска, введя новую цель, если результат окажется неудовлетворительным. Под сужением области поиска здесь имеется в виду вмешательство ЛПР в процессе работы алгоритма и уточнение цели на основе уже имеющихся промежуточных результатов поиска.

Ограничения на время выполнения задач

В работе рассматриваются случаи со сложными зависимостями между задачами. Как уже было сказано выше, зависимости подразделяются на три вида:

• “Одновременный старт” (необходимость одновременного начала)
  
• “В течение” (зависимая задача должна быть выполнена в тече)
  
• “Конец к началу” (зависимая задача должна начать выполняться после окончания той, от которой она зависит)
  

Пусть задачи t1 и t2 связаны по правилу “Одновременный старт”. Очевидно, что если t1 зависит от t3 по правилу “Конец к началу”, t2 так же будет зависеть от t3 по правилу “Конец к началу”.

Предположим, t1 должна быть выполнена в течение задачи t2, то есть t1 зависит от t2 по правилу “В течение”. В этом случае если t2 зависит от t3 по отношению “конец к началу”, t1 так же переймет эту зависимость. Однако t2 не переймет зависимостей “конец к началу” задачи t1.

Так же можно показать, что цепочки зависимостей “В течение” и “Конец к началу” порождают слудующее правило:

Если справедливо, что

t1 -> t2 -> … -> tn

то



Здесь запись t1 -> t2. означает зависимость t1 от t2 по рассматриваему в выражении правилу.

Приведенные правила раскрывают неявные зависимости между задачами условия, которые так же требуется учитывать при построении расписания. По результатам теоретического и экспериментального исследования изложенных ниже способов учета зависимостей при реализации систем управления расписаниями рекомендуется раскрывать эти неявные зависимости перед началом поиска.