План исследования 8 Современное состояние проблемы 9 Описание эксперимента 10 Метод текущего Парето [7] 10 Метод moga [1] 11

Вид материала

Подобный материал:

1 2 3 4 5 6 7

Содержательное описание проблемы

Предполагается, что известен набор задач, порядок выполнения которых требуется определить. Для каждой из них определен список сотрудников, способных ее выполнить. Известно, что при достаточно большой размерности задачи построения расписания (ЗПР) время ее решения растет пропорционально экспоненте размерности задачи. Сегодня для ее решения достаточно часто используют “жадные” алгоритмы. Иногда они дают приемлемые результаты за относительно короткое время. Следующим шагом в исследовании данной проблемы должны стать поисковые методы, которые позволят лицу, принимающему решение, увидеть область доступных опций. Под областью доступных опций здесь понимается набор недоминируемых по Парето, либо какому-либо другому правилу решений. Исходя из них у него будет возможно выбрать вариант, удовлетворяющий политике компании и позволяющий, пусть не по всем, но по некоторым параметрам обойти конкурентов.

Множество Парето

В многокритериальной постановке многих задач критерии попарно несравнимы. Имея две оценки (a1,a2) и (b1,b2) и зная, что выполняется a1 > b1 и a2 < b2, нельзя сказать, какая из них предпочтительнее. Иными словами доминирует другую.

Пусть есть две векторных оценки критериев задачи {a_i} и {b_i}. Будем говорить, что {a_i} доминирует {b_i} если

. Если известны векторные оценки всех возможных вариантов решения задачи, очевидно имеет смысл исключить из рассмотрения все те из них, для которых существует хотя бы один доминирующий вариант. Множеством недоминируемых вариантов - множеством Парето - называется набор тех возможных решений задачи, для которых не существует другого решения, доминирующего его.

Метод выделения ядра

Зачастую на практике требуется не просто найти множество лучших из достижимых решений, но и выбрать из этого множества варианты, позволяющие наилучшим образом выполнить поставленную перед системой цель g. Или же составить конкуренцию аналогичным системам.

Пусть имеются два критерия: стоимость решения (q1) и его некоторое обобщенное качество (q2)

На диаграме 1 цель, которую требуется достигнуть находится внутри множества достижимых решений. Зачастую в этом случае имеет смысл выбирать доминирующие цель варианты, и рассматривать только те из них, которые дают лучший по всем показателям результат.

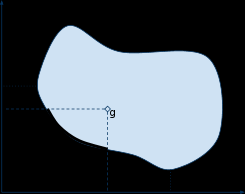
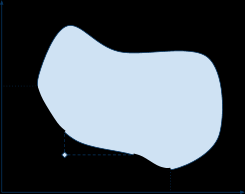
Диаграма 1 Диаграма2

В случае, изображенном на диаграме 2, поставленная цель в принципе недостижима. Если ставится задача обойти конкурирующую фирму, очевидно, доминируемые целью решения будут бесполезны. Однако выбрав, например, более качественные, но более дорогие варианты, при определенной стратегии управления можно получить конкурентное преимущество.

Специфические черты проблемы

Исследуемая задача отличается прежде всего тем, что вместо инструмента для составления единственного расписания требуется создать набор механизмов для упрощения выбора подходящего расписания из вычисляемого множества так называемых лучших вариантов.

В результате первого этапа автоматического анализа проблемы должно быть построено множество недоминируемых оценок, из которых ЛПР сможет выбрать устраивающий его вариант.

Еще одна особенность задачи заключается в том, что требуется учитывать возможность появления задачи после составления расписания. Относительно небольшие модификации набора задач не должны приводить к сильным изменениям исполняемого плана.

Так же следует учитывать, что на решение накладывается ряд ограничений. Задачи могут иметь различные зависимости друг от друга, иметь жесткие границы начала и конца выполнения. Рабочий день инженера должен начинаться и заканчиваться в определенной позиции. Приступая к следующей задаче после окончания предыдущей, специалисту необходимо переместиться в новое место выполнения.

Постановка задачи

Описание начальных условий

Приведем описание начальных условий - набор данных, предоставляемых внешними системами. Будем считать, что доступ к этой информации занимает пренебрежимо мало времени по сравнением со временем работы системы СУП.

данные о каждом работнике
1. его рабочие часы
2. задачи, которые он может выполнять
данные о каждой задаче
1. требуемый срок завершения (за несоблюдение накладывается штраф)
2. набор зависящих и зависимых задач
3. место выполнения
4. время выполнения
5. интервал времени, в течение которого выполнение задачи имеет смысл
6. набор квалифицированных сотрудников
данные о географическом положении точек работ – полносвязный направленный граф, на ребрах которого обозначено время, затрачиваемое на передвижение между двумя точками

Расписание будет состоять из времени начала выполнения для каждой задачи и сотрудника, который будет ей заниматься. По завершении поиска, как уже было упомянуто выше, мы получим приближение множества недоминируемых вариантов расписаний. Из них ЛПР сможет, руководствуясь некоторой информацией о предпочтительности вариантов, выбрать подходящий для целей предприятия.

План исследования

Проведенное исследование включает в себя сравнение эффективности различных комбинаций методов оптимизации поиска. Для проведения эксперимента были выбраны следующие подходы

1. Устранение возможности генерации заведомо неверных вариантов

2. Метод текущего Парето (М.А. Потапов, Ю.Г. Евтушенко) (модификация для дискретных множеств)

3. Ранжирование оценок по количеству доминирующих вариантов, являющийся частью многоцелевого генетического алгоритма (MOGA, multi-objective genetic algorhythm)

4. Ранжирование оценок по количеству выполненных целей, так же являющийся частью MOGA.

Виды рассматриваемых ограничений на время выполнения задач:

а. последовательное выполнение

б. выполнение в течение другой задачи

в. одновременное начало выполнения

Очевидно, что при наличии ограничений б. и в. первый из приведенных подходов необходим. Иначе на каждый правильный вариант расписания будет приходиться как минимум ((W-1)*T)^N вариантов, не удовлетворяющих ограничению б) или в). (W - общее число работников, T - число рабочих отрезков времени каждого из работников, N - число групп задач, связанных зависимостями б) или в) ). Приведенная оценка получена исходя из правила: если задачи связаны зависимостью б или в, они должны быть выполнены разными работниками в один и тот же отрезок рабочего времени. Подробнее о способах увеличения вероятности найти верный вариант, а так же о способах уменьшения длины ключа за счет этого будет сказано далее.

Blog