План исследования 8 Современное состояние проблемы 9 Описание эксперимента 10 Метод текущего Парето [7] 10 Метод moga [1] 11

Вид материала

Подобный материал:

1 2 3 4 5 6 7

Описание агоритма поиска

Алгоритм работы поиска представляется следующей блок схемой:

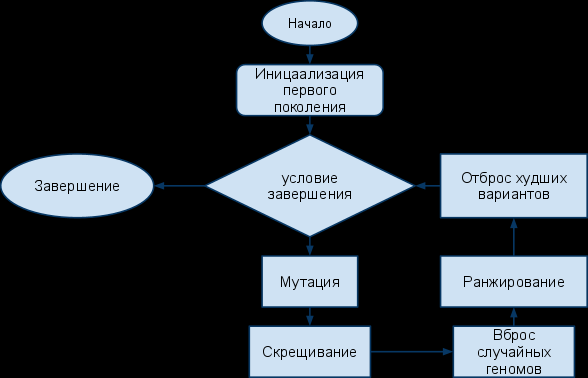
Инициализация первого поколения

На этапе инициализации выполняется случайное создание первого поколения. Ключи собираются на основе пределов подключей каждого этапа. Каждый подключ вычисляется случайно и равномерно распределен на отрезке [0,K] (K - верхний предел подключа).

Условие завершения

Для исследования были выбраны два условия завершения. На средних размерностях это неизменность текущего Парето на протяжении N поколений. N принято 20, так как за 20 поколений при 25% новых оценок в каждой итерации перебирается и отсеивается в 5 >> 1 полных поколений.

Вычислительная сложность задачи для малых размерностей позволяет охватить порядка 1000 итераций за 10 минут. Это много больше 300 итераций, в среднем требующихся для выполнения предыдущего условия. Поэтому для исследования поведения поиска на малых размерностях в качестве условия завершения было выбрано достижение тысячного поколения.

Операция мутации

Основная задача операции мутации в генетическом алгоритме - внесение относительно малого случайного изменение в аргумент p. Реализация этой операции в рассматриваемой задаче очевидна: в геноме случайным образом меняется небольшое число бит. Доля изменяемых бит была выбрана равной 10% от длины мутируемого генома.

Операция скрещивания

Задача операции скрещивания - создание новых геномов p3 и p4 на базе двух имеющихся p1 и p2. Он осуществляется случайным выбором каждого бита p3 из одного из бит соответствующей позиции p1 и p2. p4 формируется аналогично. Если на i-ю позицию p3 был выбран бит i-й позиции p1, то на i-ю позицию p4 будет выбран бит с i-й позиции p2. Доля “обмениваемых” в процессе скрещивания так же равняется с = 10%.

Проиллюстрируем физический смысл скрещивания. Пусть длина генома равна n бит. Его можно представить как точку в одной из вершин гиперкуба размерности N. Если рассмотреть возможные пути из p1 в p2 по вершинам этого гиперкуба длины 2*с, то в результате операции скрещивания мы получим две точки одного и того же пути, отстоящие от p1 и p2 на одинаковое число шагов.

Результаты эксперимента

Эксперимент приводился для каждого из пяти перечисленных выше порядков ранжирования и для двух наборов начальных условий. 4 инженера, 20 локаций, 5 групп задач и 20 инженеров, 100 локаций, 50 групп задач.

Каждая группа задач включала в себя все три типа зависимостей, каждой задаче присваивалась локация на основе равномерного распределения. На иллюстрации приведены длительности каждой из задач и их зависимости.

Ниже описаны результаты проведенных вычислений (количество рабочих, количество локаций, количество комплектов задач). Все временные параметры приведены в милисекундах.

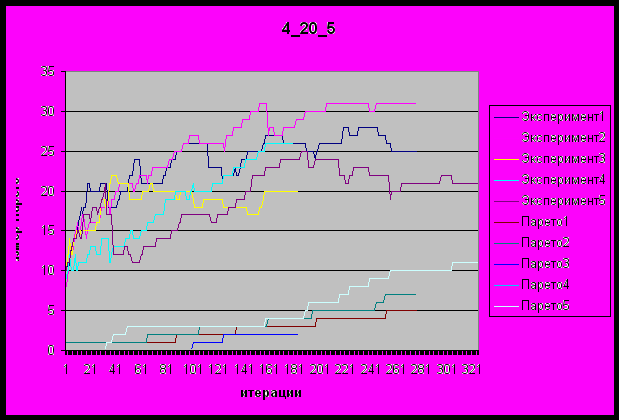
Эксперимент “4,20,5”

Время обработки поколения:

Размер поколения	100	200
Среднее время обработки поколения	0,5 сек	1,3 сек

Для анализа результатов эксперимента полезно выделить общее множество Парето по всем пяти шагам эксперимента и сравнить, насколько парето каждого шага приблизилось к нему. Это имеет смысл, так как помимо размера множества Парето и доли элементов общего Парето в нем нас интересует, насколько недоминируемые оценки каждого эксперимента, не попавшие в общее Парето, близки к нему.

Первый эксперимент проводился при размере поколения 100 и условии завершения – 20 итераций без изменения текущего Парето.

Шаг	Размер вычисленного Парето	Вычислено решений общего Парето	средние ошибки	максимальные ошибки
РГ -> МТП -> ММД -> КДЦ	25	5	[647; 0; 1]	[1300; 0; 3]
МТП -> РГ-> ММД -> КДЦ	31	7	[623; 0; 1]	[1300; 0; 3]
РГ-> ММД -> КДЦ	20	2	[716; 300; 1]	[2200; 300; 3]
МТП -> ММД -> КДЦ	26	0	[833; 0; 1]	[2000; 0; 3]
МП -> ММД -> КДЦ	21	11	[640; 0; 1]	[1600; 0; 2]

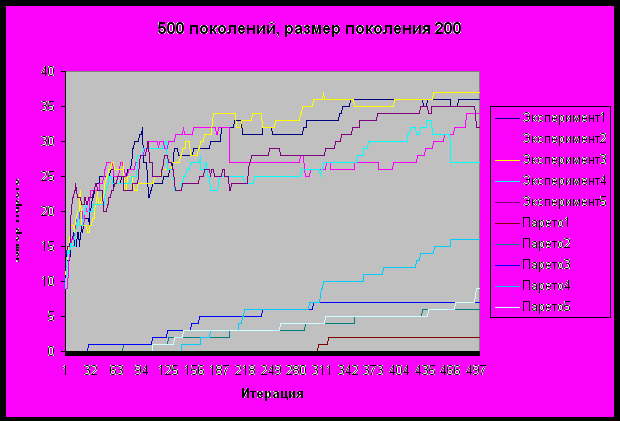
На приведенном ниже графике проиллюстрирована эволюция текущего множества Парето (Эксперимент<#>) и эволюция доли решений поколения в общем Парето, найденном по результатам всего эксперимента (Парето<#>).

Результаты измерений с условием завершения – достижение 500 поколений.

Для размера поколения 100:

Шаг	Размер вычисленного Парето	Вычислено решений общего Парето	средние ошибки	максимальные ошибки
РГ -> МТП -> ММД -> КДЦ	30	4	[718; 300; 1]	[1700; 300; 3]
МТП -> РГ-> ММД -> КДЦ	30	4	[730; 0; 1]	[1900; 0; 2]
РГ-> ММД -> КДЦ	28	7	[842; 0; 1]	[4900; 0; 2]
МТП -> ММД -> КДЦ	27	9	[535; 300; 1]	[1200; 300; 2]
МП -> ММД -> КДЦ	25	8	[1493; 300; 1]	[4000; 300; 3]

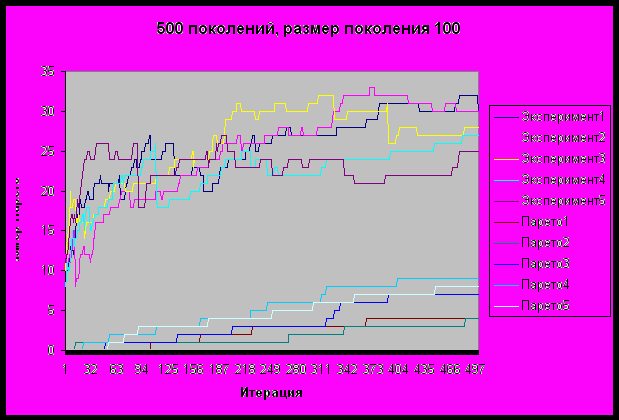
Результаты измерений с условием завершения – достижение 500 поколений.

Для размера поколения 200:

Шаг	Размер вычисленного Парето	Вычислено решений общего Парето	средние ошибки	максимальные ошибки
РГ -> МТП -> ММД -> КДЦ	36	2	[460; 300; 1]	[1300; 300; 2]
МТП -> РГ-> ММД -> КДЦ	34	6	[484; 300; 1]	[1200; 300; 3]
РГ-> ММД -> КДЦ	37	7	[435; 0; 1]	[900; 0; 4]
МТП -> ММД -> КДЦ	27	16	[463; 0; 1]	[1100; 0; 1]
МП -> ММД -> КДЦ	32	9	[585; 0; 1]	[2200; 0; 3]

Blog