К. А. Джафаров курс лекций «исследования в рекламе» Содержание (по темам) Особенности рекламного исследования Процесс рекламного исследования Этика рекламных исследований Отчет

Вид материала

Курс лекций

Содержание 10. Описательные методы анализа количественных данных Дескриптивные методы. Доли, проценты и пропорции Описательные статистики Медиана (Ме) X, которому соответствует наибольшее значение ν Выводы об одном параметре на основе одной выборки Выборка большого объема, интервальный или относительный уровень измерения. Выборка небольшого объема, интервальный или относительный уровень измерения. Выводы об одной переменной на основе двух независимых выборок Небольшая выборка, интервальный или относительный уровень измерения Выводы о связи переменных Выводы о поведении одной переменной в трех и более независимых выборках 11. Конкуренция и конкурентное окружение Применение КА. Выдвижение гипотез исследования или формулировка вопросов, которые ставятся перед ними Планирование выборки и получение рекламных материалов Определение способа обработки дублирующиеся рекламы Подготовка кодировочных таблиц и бланков Применение результатов ... Полное содержание

Подобный материал:

• Московская финансово-юридическая академия, 21.17kb.
• Планирование программы исследования: основные этапы. Постановка задач маркетингового, 30.98kb.
• Разработка научно-образовательного материала (ном), 36.8kb.
• Маркетинговые исследования фактически это деятельность, направленная на анализ и сбор, 41.83kb.
• Инструкция : Бланк исследования: все без бланков исследования Отчет испытуемого, 39.61kb.
• Задача: формирование методологической готовности к научно-исследовательской деятельности, 702.35kb.
• Отчет по нир: 44 с., 34 рис., 2 табл., 16 ист. Объекты исследования рабочий процесс, 404.5kb.
• Отчет по результатам социологического исследования, 2088.05kb.
• Эффективность исследования систем управления и решения возникающих проблем во многом, 32.47kb.
• Разработка программы укрепления репутации вуза Математические модели в управлении рекламными, 29.46kb.

10. Описательные методы анализа количественных данных

Когда данные собраны, начинается их анализ, т.е. организация данных, изучение и применение статистических критериев. При анализе данных используются различные методы. Рассмотрим в начале

Дескриптивные методы. Данные можно описывать в терминах распределения частот, долей, процентов и пропорций.

Распределение частот. Каждого ответа относят к одной из категории шкалы. При этом, ставят отметку возле той категории, к которой отнесен ответ. Окончательный результат подсчета числа ответов по каждой из категорий называется распределением частот. Подсчет можно выполнить вручную или на компьютере.

Доли, проценты и пропорции. После построения распределения частот выбирается один из трех типов анализа:

- доли (отражают относительную частоту ответов в категории, получается делением числа ответов конкретной категории к общему числу ответов по всем категориям),

- проценты (вычисляются путем деления количество ответов к общему числу ответов и умножением на 100),

- пропорции (пропорция одного числа X в отношении другого числа Y определяется как X/Y, дает возможность отчетливо видеть соотношения между относительным размером двух категорий, использованных в анкетном вопросе).

При анализе данных используются дискретные и непрерывные данные. Дискретные данные содержат ответы, ограниченные конкретным набором целых чисел, отделенных друг от друга одинаковыми интервалами, непрерывные данные дают возможность для ответа, при которой значения могут располагаться как угодно близко друг другу на числовой шкале. Эти данные обычно группируются:

- упорядочиваются,

- определяется число и ширина интервалов категорий,

- строится распределение частот.

Описательные статистики. При сборе данных на интервальном и относительном уровне используется статистический анализ. В основном следующие статистики:

Среднее

г
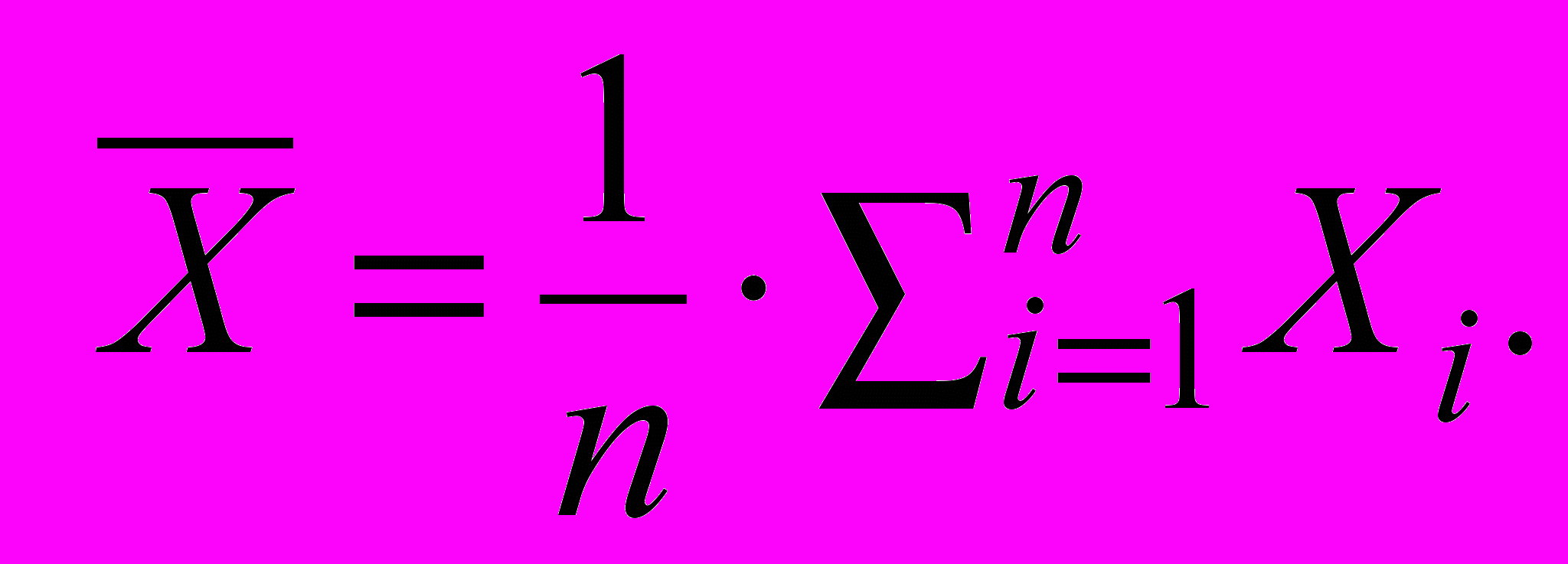
де Xi – наблюдаемые данные, n – их количество. При интервальном измерении Xi – середина интервалов. Среднее дает возможность представить единственным числом множество ответов на вопрос анкеты.

Стандартное отклонение

.

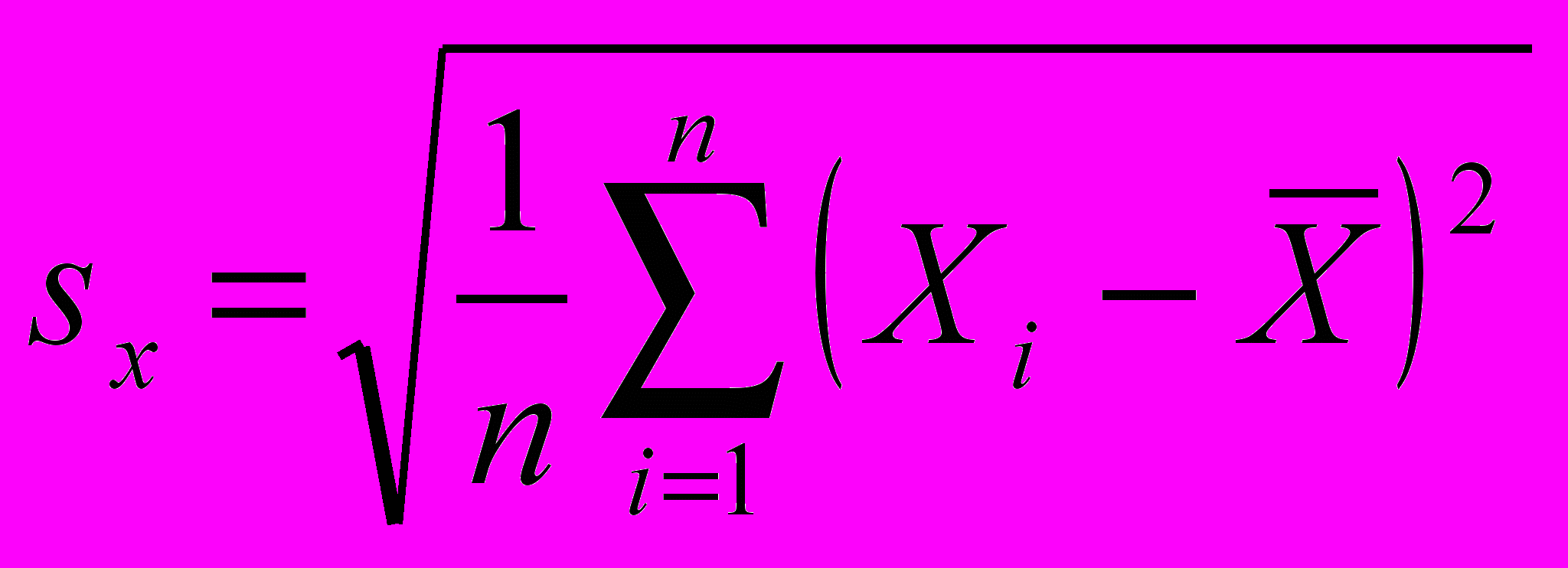Дисперсия – это квадрат стандартного отклонения. Стандартное отклонение и дисперсия выражают меру отклонения (разброса) значений около среднего.

Медиана (Ме) – это то значение выборки, которое находится в середине вариационного ряда. Если вариационный ряд дискретный, то в случае, когда n – нечетное число, медиана - это то значение выборки, которое находится ровно в середине вариационного ряда. Если n – четное число, то медиана определяется как среднее арифметическое двух выборочных значений, которые находятся в середине вариационного ряда.

Если вариационный ряд интервальный, то в этом случае определяется медианный интервал, который находится в середине. С помощью линейной интерполяции находится медиана. Здесь мы опустим процедуру нахождения. Приближенно значение медианы в этом случае можно определить следующим образом. Пусть все выборочные значения попадают в промежуток от (a,b). Составим таблицу

(a,a1)	(a1,a2)			(am-1,b)
ν1	ν2			νm

где ν – количество выборочных значений X, попадающих в интервал. Вычислим




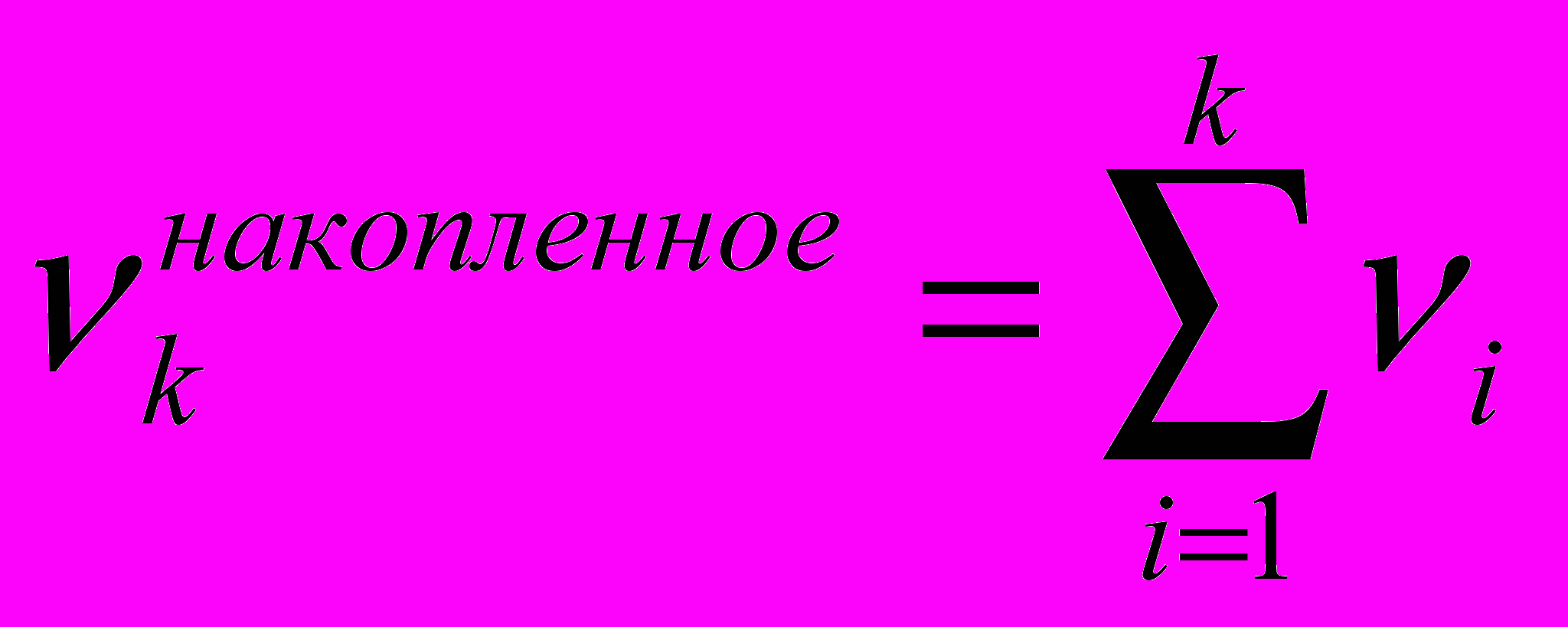
Медиана – это то значение выборки, для которого .

Если в выборке разброс крайних значений существенен, то в качестве выборочной характеристики среднего лучше использовать медиану (а не )

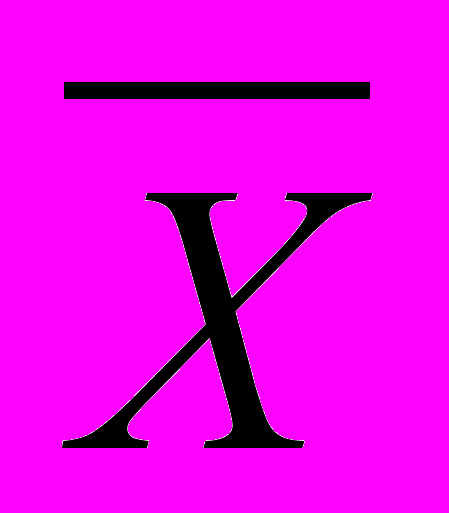Мода (Мо) – это то значение выборки, которое имеет наибольшую частоту (т.е. это часто встречающееся значение выборки). Если вариационный ряд дискретный, т.е. имеет следующий вид

X(1)	X(2)			X(n)
ν1	ν2			νn

то мода – это то значение X, которому соответствует наибольшее значение ν.

Для принятия решения помимо описательного анализа нужен статистический анализ. Исследователь должен быть уверен в выводах, которые он делает. Он должен знать, какой доверительный уровень выбрать. Одни распределения симметричны, другие нет, что у симметричных распределений значения среднего, медианы и моды совпадают. Он должен знать о правиле трех-сигм: 68% собранных данных (по определенному признаку) находятся от среднего на расстоянии не больше чем значения стандартного отклонения, 95,4% - на расстоянии не больше чем двух стандартных отклонений, а 99,7% - на расстоянии не больше чем трех стандартных отклонений…

После вычисления выборочных характеристик исследователь делает выводы, основываясь на субъективных рассуждениях, если не воспользоваться методами статистических выводов. Если он хочет получить выводов с высоким уровнем доверия должен применить статистический анализ. С помощью такого анализа он получает математическую оценку уровня доверия и определяет статистическую значимость различий в ответах разных групп. Методы статистических выводов используют гипотезы: основные и альтернативные. Основная гипотеза – утверждение об отсутствии различий связи, или иных закономерностей. Альтернативы бывают односторонние и двусторонние. После выдвижения гипотез исследователь определяет уровень значимости, т.е. вероятность отвергнуть основную гипотезу, когда она на самом деле верна. Рассмотрим более подробно.

Выводы об одном параметре на основе одной выборки.

Возможны два типа анализа.

А. Сравнение выборочного среднего или доли с соответствующим средним или долей генеральной совокупности.

Б. Исследование внутренних свойств одной выборки.

Сначала остановимся на первом типе анализа. Займемся сравнением средних значений. Здесь также есть варианты.

1. Выборка большого объема, интервальный или относительный уровень измерения. Символически, основная и альтернативная гипотезы записываются так:

Н0: X = μ

Н1: X > μ (или X< μ, или двусторонняя: X = μ)

Здесь – X выборочное среднее, а μ – среднее генеральной совокупности. Для проверки гипотез используется критерий (или тест), который предусматривает вычисление статистики критерия Z = (X- μ)/(σ/√n), которая имеет стандартное нормальное распределение. Отметим, что в этой формуле σ стандартное отклонение генеральной совокупности. Далее, из таблицы значений функции стандартного нормального распределения (см.приложение) находят при заданном уровне значимости критическое значение критерия Zкрит, которого сравнивают с Z. Если Z > Zкрит., то основная гипотеза отвергается.

2. Выборка небольшого объема, интервальный или относительный уровень измерения. Выдвигаются такие же гипотезы, как и в пункте 1. Только используется другой критерий t = (X- μ)/(s/√n), где s выборочное стандартное отклонение. Эта статистика подчиняется распределению Стьюдента. Из таблицы значений распределения Стьюдента с заданным уровнем значимости и числом степеней свободы n-1, находят критическое значение tкрит. Если t > tкрит, то основная гипотеза отвергается.

Б. Рассмотрим второй тип и задачу сравнения долей. Для этого выдвигаются гипотезы:

Н0: p = Pи

Н1: p > Pи,

где p доля выборки, включающая выбравших целевой вариант ответа, Pи доля респондентов генеральной совокупности, выбравших целевой вариант ответа. Для проверки гипотез вычисляется статистика критерия Z = (p-Pи)/√Pи•Qи/n), где Qи доля респондентов, выбравших альтернативный вариант ответа, n объем выборки. Далее, также из таблицы значений стандартного нормального распределения при заданном уровне значимости находят Zкрит. И сравнивают с Z. Если Z > Zкрит, то основную гипотезу отвергают.

С помощью критерия хи-квадрат мы можем исследовать распределение частот в одной выборке, и определить, имеется ли значимое отличие этого распределения от некоторого теоретического распределения. Этот критерий применяется для данных любого уровня измерения. Логика критерия в том, что чем больше наблюдаемая частота отличается от ожидаемой частоты, тем больше вероятность существования действительных различий между категориями ответов. Таким образом, при использовании критерия хи-квадрат основная гипотеза утверждает, что наблюдаемые частоты эквивалентны ожидаемым, а альтернативная гипотеза утверждает что, они не равны. Статистика этого критерия Χкв = Σ (Qi – Ei)кв/Ei , где Ei ожидаемая частота i-ой категории, а Qi наблюдаемая частота той же категории. Далее, из таблицы значений распределения хи-квадрат при заданной уровне значимости и числе степеней свободы (подробно на примере) находят критическое значение и сравнивают с вычисленной статистикой.

Выводы об одной переменной на основе двух независимых выборок.

1. Большая выборка, интервальный и относительный уровень измерения. Рекламисты часто сравнивают группы людей. Их могут интересовать группы, отличающиеся по какой-либо переменной, связанной с рекламированием: по осведомленности о рекламе, по степени воздействия на них рекламы, по воздействию на них различных типов рекламы, сравнение потребителей, которые используют данную марку, с теми, кто ею не пользуется, молодых потребителей с пожилыми потребителями и т.д. Здесь применяется критерий: Z = (X1-X2)/√(s1кв/n1)+(s2кв/n2), где X1 и X2 выборочные средние, а s1 и s2 выборочные стандартные отклонения двух выборок, соответственно, n1 и n2 объемы этих выборок. Далее, из таблицы значений стандартного нормального распределения при заданном уровне значимости находят Zкрит. Если Z > Zкрит, то основную гипотезу отвергают.

2. Небольшая выборка, интервальный или относительный уровень измерения. При постановке задачи, как в пункте 1 выше, используется критерий Стьюдента. Вычисляется статистика

t = (X1-X2)/ √((n1-1)s1кв + (n2-1)s2кв))/(n1+n2-2) •(1/n1 + 1/n2).

Далее из таблицы значений распределения Стьюдента при заданном уровне значимости и числе степеней свободы n1+n2-2 находят tкрит и сравнивают с t.

В заключение этого пункта отметим, что помимо сравнения двух средних, рекламисты часто сравнивают и доли в двух выборках.

Здесь используется и значение стандартной ошибки для разности долей (а не разность двух средних)

Z = (p1-p2)/ √ ((n1•p1+n2•p2)/(n1+n2)) •(1-((n1•p1+n2•p2)/(n1+n2))) (1/n1 + 1/n2).

Выводы о связи переменных.

Простой и наглядный способ исследования отношений между переменными является их оформление в виде перекрестной таблицы. Такая таблица позволяет узнать, как респонденты, имеющие определенное значение по одной переменной, характеризуются с точки зрения другой переменной или переменных. Таблица строится так:

1) на горизонтальной оси указываются названия или значения для каждой категории первой переменной,

2) на вертикальной оси указываются значения или названия для каждой категории второй переменной,

3) для каждого респондента находят категорию или значение на горизонтальной оси, которые соответствовали бы его ответу на данную переменную,

4) для того же респондента находят категорию или значение на вертикальной оси, которые соответствовали бы его ответу,

5) ставят галочку в клетке на пересечении горизонтальной и вертикальной осей,

6) подсчитывают количество галочек в каждой клетке и, исходя из полученных результатов, определяют проценты для каждой строки и каждого столбца, а также для каждой клетки.

Связь между переменными определяется с помощью корреляционной матрицы.

Выводы о поведении одной переменной в трех и более независимых выборках.

Описанные выше критерии применимы тогда, когда необходимо оценить различия между двумя сравниваемыми средними, полученными в двух группах. Эти критерии неприемлемы, если нужно сравнить три или более средних. Во-первых, они неэффективны (сравнение, например пяти средних требует вычисления десяти коэффициентов корреляций). Во-вторых, они могут привести к неправильным выводам. Для устранения этих проблем применяется дисперсионный анализ (ДИ).

Однофакторный ДА применяется к одной зависимой переменной, такой, как например, намерение купить определенный товар, и сравнивает среднее этой переменной в трех и более независимых группах. Н0 предполагает, что средние равны, а Н1 предполагает, что различия в значениях сравниваемых средних больше, чем можно ожидать, исходя из ошибки выборки. ДА требует сложных расчетов, поэтому использует компьютерные программы. Но, исследователь должен понимать логику ДА.

ДА проводится в следующей последовательности:

1. вычислите общее среднее,
   
2. вычислите сумму квадратов между группами (СКМ), которая определяется как сумма квадратов разностей каждого группового среднего и общего среднего, помноженных на число респондентов в каждой группе,
   
3. подсчитайте степени свободы (СС) для СКМ, отняв единицу от количества групп,
   
4. подсчитайте средний квадрат между группами (СрКМ), который определяется как отношение СКМ к СС,
   
5. подсчитайте сумму квадратов внутри групп (СКВ),
   
6. подсчитайте степени свободы для СКВ, отняв от общего количества людей в выборке количество групп,
   
7. определите внутригрупповую вариативность, т.е. средний квадрат внутри групп (СрКВ), как отношение СКВ к СС,
   
8. находите значение F-статистики как отношение СрКМ к СрКВ.
   

Если F < 1, то внутригрупповая дисперсия больше межгрупповой дисперсии, и основная гипотеза отвергается.

Заметим, что во избежание ошибок при этом, необходимо выполнить три основные требования:

- статистический критерий является основой суждения, а не заменяет его (статистически значимые различия средних говорят о том, что различия вызваны реально существующими различиями в генеральной совокупности, а не обусловлены случайной ошибкой),

- не забывайте о зависимости статистики хи-квадрат от объема выборки (если Ei < 5, то хи-квадрат не применяется),

- корреляция не позволяет делать выводы о причинно-следственных отношениях (указывает только на взаимосвязь).

В заключение этого пункта, приведем сводную таблицу критериев с указанием обстоятельств, определяющих их применение.

Сравнение	Объем выборки	Уровень измерения	Статистика критерия
Выборочного и теоретического средних	большой	интервальный или относительный	Z-критерий
_____ !!______	небольшой	интервальный или относительный	t-критерий
Выборочной и теорет. долей	любой	номинальный	Z-критерий для долей
Двух выборочных средних	большой	интервальный или относительный	Z-критерий
_____!!_______	небольшой	интервальный или относительный	t-критерий
Долей в двух выборках	любой	номинальный	Z-критерий для долей
Одна и более переменных	любой	номинальный, интервальный или относительный	Критерий хи-квадрат
Взаимосвязи двух переменных	любой	номинальный, интервальный или относительный	корреляция
Три или более выборочных средних	любой	интервальный или относительный	Дисперсионный анализ

11. Конкуренция и конкурентное окружение

А. Контент-анализ (КА) рекламы. Под этим понимают метод количественных исследований, с помощью которого можно лучше понять практику рекламной деятельности, стратегии рекламирования конкретной торговой марки, а также оценить воздействие рекламы.

Характерные особенности и применение КА.

КА – это систематический, объективный метод количественных исследований. КА будет объективным, если:

- выработаны ясные и объективные правило отбора и изучения рекламы,

- четко определены категории кодирования,

- кодировщики и исследователи прошли хорошую подготовку и работают независимо друг от друга,

- анализ данных соответствует уровню измерения собираемой информации.

Так как КА один из количественных методов, то представление результатов такого анализа дает возможность пользоваться статистическими методами в процессе изучения и обобщения результатов, увеличивает возможность обнаружения глубинных зависимостей в данных.

Применение КА. Этот метод применяется в научных, и в прикладных целях. В научных исследованиях КА направлен на установление общих тенденций развития практики рекламной деятельности или определения зависимости между характерными особенностями рекламы и рекламным воздействием. В прикладных исследованиях КА направлен на определение позиционирования товара и установление рекламной стратегии конкурирующих торговых марок.

Этапы проведения КА.

1. Выдвижение гипотез исследования или формулировка вопросов, которые ставятся перед ними.

2. Формулировка операционального определения генеральной совокупности изучаемых рекламных материалов. Операциональное определение соответствует вопросам исследования или выдвигаемой гипотезе, и подобно определению генеральной совокупности при проведении опросов, четко указывает на совокупность объектов, представляющих интерес.

3. Планирование выборки и получение рекламных материалов. План выборки определяет способ отбора конкретной рекламы из числа объектов, названных в определении рекламных материалов (сплошное или выборочное обследование).

4. Определение способа обработки дублирующиеся рекламы.

5. Разработка системы категорий. В два этапа: а) установление категорий, представляющих интерес, б) перечисление конкретных параметров каждой категории. В данном этапе также выбирается тип уровня измерения.

6. Подготовка кодировочных таблиц и бланков. Кодировочная таблица – это словарь КА, содержащий определения наиболее важных терминов. Кодировочный бланк напоминает анкету, составляемую для проведения опроса. Сюда вносят результаты наблюдения лиц, осуществляющих изучение и оценку рекламы.

После создания кодировочных таблиц и бланков, отбираются кодировщики, и проводится их обучение. После устных инструкций переходят к практической деятельности по кодированию, во время которой кодировщикам демонстрируют отобранные образцы рекламы, они присваивают этим образцам коды, и обсуждаются проблемы, с которыми столкнулись кодировщики, и происходит обмен опытом. Чтобы улучшить КА, можно провести предварительное тестирование и последующий пересмотр материалов. Пилотаж дает возможность улучшить структуру системы категорий, дает более точное определение категориям, усовершенствует процедуру и инструментарий для кодирования.

Проверка надежности является важным моментом КА. Есть различные формулы для определения надежности, они предназначены для анализа данных на номинальном уровне измерения. Согласованность экспертных оценок для данных на интервальном уровне определяется с помощью коэффициента корреляции.

Применение результатов исследования. Это заключительный этап КА. Достигнутое понимание должно быть сформулировано в явном виде. Результаты изучения зависимости между формой рекламы и ее содержанием является возрастания понимания того, как особенности рекламы определяют реакцию на нее потребителей. В обоих случаях более глубокое понимание приводит к расширению и внесению изменений в существующую теорию. Наконец, проводя КА товарной категории или конкретной марки, можно глубже понять рекламную стратегию и практику конкурентов, что, в свою очередь, позволяет усовершенствовать стратегическое планирование рекламы собственной торговой марки.

Процесс построения карт восприятия. Карты восприятия – это средство получения информации, необходимой для понимания указанных аспектов оценки потребителем торговой марки товара. Существуют два подхода к составлению карт восприятия: атрибутный и не атрибутный подходы.

Атрибутный метод требует от респондентов оценки набора торговых марок с помощью большого количества свойств (атрибутов), на которые они ориентируются, когда воспринимают, оценивают и определяют различия между торговыми марками или товарами. Атрибутные карты создаются с помощью одного из трех статистических методов: факторного анализа, дискриминантного анализа и анализа соответствий.

Неатрибутный метод требует от респондентов оценки торговых марок в терминах сходства или предпочтения, а не на основании свойств.

Факторный анализ (ФА). Статистический метод, устанавливающий небольшое число факторов или осей, которые определяют взаимосвязь между большим количеством коррелируемых между собой переменных. ФА применяется после того, как потребители дали оценку каждой рассматриваемой торговой марке или товару по всем атрибутам. Вычисляют коэффициент корреляции, далее:

- компьютерная программа ФА изучает корреляционную матрицу, а затем извлекает достаточное число факторов, объясняющих 100% совокупной дисперсии,

- программа вычисляет для каждого фактора три важных показателя,

- на основании изучения собственных значений и процента объясненной дисперсии по каждому из факторов исследователь определяет, сколько факторов следует оставить для последующего анализа,

- с помощью компьютерной программы ФА проводится повторный анализ данных, при этом количество выделяемых факторов устанавливается равным числу, полученном на предыдущем этапе,
- для каждой переменной вычисляются и изучаются факторные нагрузки, которые служат показателем связи между переменной и фактором,

- исследователь изучает атрибуты, составляющие каждый фактор, и затем дает ему название,

- с помощью программы ФА вычисляется средний факторный балл для каждой торговой марки (факторный балл – это взвешенная средняя оценка торговой марки по всем атрибутам, составляющим данный фактор),

- средний факторный балл используется при размещении торговых марок на карте восприятия.

Дискриминантный анализ (ДА). ФА уменьшает список атрибутов торговых марок и сводит его к нескольким факторам, в соответствии с которыми торговые марки затем располагаются на карте. В результате торговые марки так группируются, что в пределах одной группы потребители воспринимают торговые марки как более сходные и отличающиеся от марок других групп. Чем больше расстояние между группами торговых марок на карте, тем больше отличаются между собой марки этих групп. ДА также использует математические вычисления для определения новых координатных осей и расположения в соответствие с ними товаров на карте восприятия. Однако в этом случае факторы определяются таким образом, чтобы свести к минимуму пересечение группировок торговых марок. Цель ДА состоит в поиске таких осей, которые как можно лучше позволяют отделить, разделить торговые марки и товары. Но, ФА позволяет создавать более наглядные и полезные карты восприятия.

Анализ соответствий (АС). ФА и ДА требуют, чтобы восприятие и оценка торговой марки осуществлялись на интервальном уровне измерения. Именно поэтому, для оценки атрибутов используют шкалы семантического дифференциала и шкалы Ликерта. Многие из атрибутов товаров могут быть измерены только на номинальном и порядковом уровнях. В этом случае, АС позволяет создавать карты восприятия на основе данных номинального и порядкового уровней измерения. Процесс проведения АС: выделяются факторы (оси), вычисляется процент дисперсии, объясненный каждым фактором, выбираются значимые факторы, которым присваиваются имена, по каждому из параметров подсчитываются баллы торговой марки или товара, атрибуты торговой марки или товар наносятся на карту.

Построение неатрибутных карт восприятия. Построение не требует составления перечня свойств торговых марок, товаров или товарных категорий. Потребители определяют сходство или предпочтение марок, исходя из тех критериев, которыми они обычно пользуются в подобных случаях. Атрибуты или иные явно указанные критерии не предоставляются исследователю. Построение по этапам.

1. Выбор типа оценки. Оценки бывают двух типов:
   

- если требуется оценка сходства и различий потребителю представляют список торговых марок с просьбой проранжировать пары, начиная с самых похожих и заканчивая самыми непохожими, и наоборот,

- если требуется оценка предпочтений, потребителю предлагают список отдельных торговых марок с просьбой упорядочить их, начиная наиболее предпочитаемой и заканчивая наименее предпочитаемой.

2. Отбор торговых марок или товаров. Необходимо отобрать достаточное количество торговых марок, принимая во внимание математическое соображение, при этом, не слишком усложняя задачу респондента.

3 . Составление вопросов для анкеты.

4. Сбор и анализ данных, построение карты. Анализ данных напоминает подход, используемый в ФА, с той разницей, что математические вычисления отличаются: 1) для каждого фактора вычисляются собственные значения и отбираются те факторы, у которых собственные значения выше, 2) располагая установленным числом параметров, для каждого объекта по каждому из факторов вычисляется балл. Эти баллы используются для построения карты восприятия.

В заключение отметим, что оба метода построения карт восприятия имеют свои преимущества и недостатки. Если использовать атрибутные методы, значения параметров легко определяются. Более того, статистические методы, лежащие в основе создания этого типа карт, просты в использовании и имеются в большинстве компьютерных статистических программ. Недостаток этого метода заключается в том, что для построения карты необходимо составить полный перечень свойств торговых марок и товаров. Если в перечень свойств внесены не все характеристики, это значительно повлияет на качество выводов, сделанных на основе карт восприятия. Неатрибутные карты восприятия полагаются на явно не указываемые критерии оценок каждого респондента. Для построения таких карт не нужно располагать перечнем атрибутов, благодаря чему подготовка и сбор информации облегчаются. Однако следует учитывать то, что факторы, выделяемые в ходе построения неатрибутных карт восприятия, зачастую сложно интерпретировать.