Geum.ru

Доклад: «Численный метод решения уравнений, неравенств и их систем»

Вид материалаДоклад

Содержание


Способ проб
Подобный материал:
Доклад: «Численный метод решения уравнений, неравенств и их систем».


Наряду с аналитическим и графическим методами широкое применение находит численный метод решения уравнений, неравенств и их систем. В последнее время интерес к этому методу возрос в связи с прогрессом в области вычислительной техники. Рекомендуется с использованием современных вычислительных средств решать численным методом уравнения, неравенства и их системы.

В самом общем виде сущность численного метода состоит в следующем: пусть каким-либо путем определены границы корня данного уравнения, произведя серию последовательных вычислений, мы сужаем границы корня так, что он может быть представлен с любой степенью точности. Рекомендуется с учащимися рассмотреть способ проб.

Способ проб основан на следующем утверждении: если функция у = F(х) непрерывная на отрезке [а, в] и F(а) < 0, F(в) > 0(или F(а)> 0, F(в) < 0), то внутри отрезка [а, в] существует точка х1 такая, что F(х1) = 0 (рис. 1).


Пусть имеем уравнение F(х) = 0, далее известно, что F(а) < 0, F(в) > 0 и функция у = F(х) на отрезке [а,в] непрерывная, тогда согласно вышеуказанному утверждению данное уравнение имеет корень х1 , заключенный между а и в. Чтобы уточнить значение корня, рекомендуется брать последовательно а1, а2, … , ап , удовлетворяющие условиям а <а1 <а2 <а3 <… <ап-1 <ап< в,

F ( а п-1) < 0, F ( ап) >0.

Тогда получим а п-1< х < а п (рис. 1). Величина разности а п-1 – а п характеризует точность, с которой найден корень х 1.Обычно полагают х 1 ≈а , или х 1 ≈а п-1 , или х 1 ≈( а п-1 + а п )/ 2.

Приближаться к корню рекомендуется не только слева, но и справа. В этом случае берем последовательно числа в , в, …, удовлетворяющие условиям а< в п< в п-1< …<в 2< в 1< в ,

F ( в п-1) >0, F ( вп) <0.

Тогда имеем вп < х1< вп-1 .




Пример 1. Вычислить способом проб корни уравнения х² – √х – 1 = 0 с точностью до 0,001.






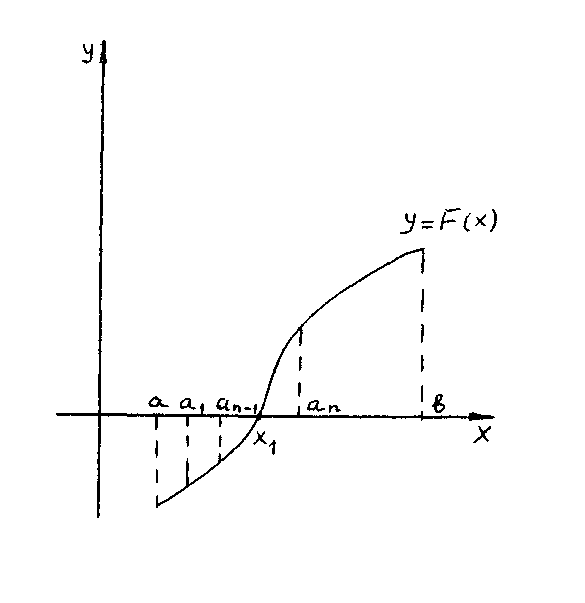
Рекомендации к решению. Вначале найдем интервалы, в которых содержатся корни данного уравнения. Построив графики функций у = √х и у = х² - 1, убеждаемся, что данное уравнение имеет один корень, лежащей на отрезке [1,4; 1,7].


Далее выполним вычисления, результаты которых приводятся в следующей таблице:

х
х² – √х – 1

В = 1,700
+0,586

В 1= 1,600
+0,295

В2=1,500
+0,025

В3=1,495
+0,011

В4=1,491
+0,002

В5 =1,490
- 0,001

Ответ: х 1 ≈ 1,400.

Если требуется способом проб решить неравенство F ( х) >0, то вначале рекомендуется этим способом вычислить все действительные корни уравнения F ( х) = 0. Пусть х 1 <х 2 <… <х п, тогда определим знак функции у = F ( х) в интервалах ( -∞ ,х 1), ( х 1,х 2), …, ( х п,∞) . для этого достаточно определить знак функции в любой точке интервала, только в силу непрерывности функция будет иметь этот знак во всем интервале. Те интервалы, в которых знак функции совпадает со знаком данного неравенства, будут его решениями.

Пример 2. решить способом проб неравенство х² – √х – 1 >0. Границы интервалов, являющихся решением неравенства, вычислить с точностью до 0,001.

Рекомендации к решению. Соответствующее данному неравенству уравнение решено выше. Это уравнение имеет единственный корень х 1 ≈1,490.Таким образом, имеем два интервала (0,х 1) и (х 1,∞ ). Интервал ( -∞ ,0) исключаем из рассмотрения, так как он не входит в область определения данного неравенства. Определим знаки функции у = х² – √х – 1 в интервалах ( 0 ,х 1) и ( х 1, ∞). В интервале ( 0 ,х 1) эта функция отрицательна, так как у(1) = -1< 0; в интервале ( х 1, ∞) эта функция положительная, так как у(4)=13 >0. Знак этой функции совпадает со знаком данного неравенства во втором интервале.

Ответ: х 1 < х < ∞, где х 1 ≈ 1,490.






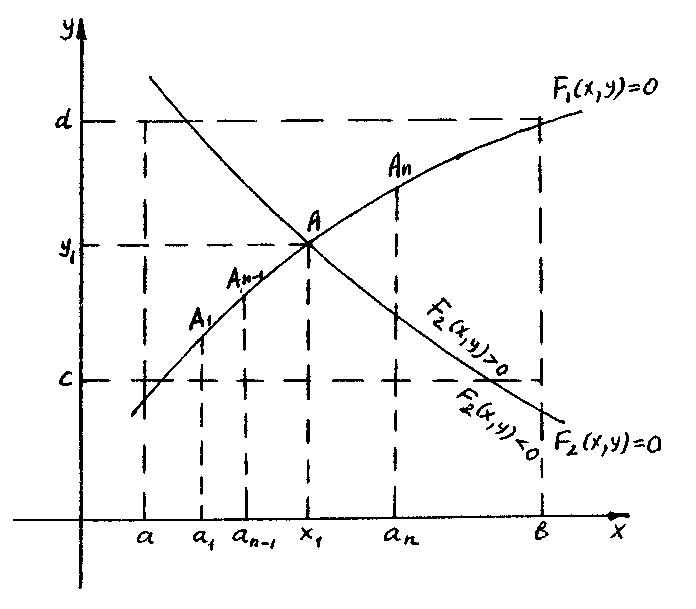
Способ проб рекомендуется использовать также при решении систем уравнений. Пусть имеем систему F1 (х;у) = 0, F2(х,у) = 0. Определим прямоугольник, в котором содержится решение этой системы. Пусть а ≤х F1 (х;у) = 0, F2(х,у) = 0 ≤ в, с ≤ у1 ≤d и функции F1 (х;у) = 0, F2(х,у) = 0 в этом прямоугольнике непрерывные. Для определенности положим, что под графиком уравнения F2(х,у) = 0в этом прямоугольнике F2(х,у) = 0, тогда в точках выше данного графика F2(х,у) > 0. Чтобы уточнить решение системы А(х1,у1) рекомендуется выбрать последовательно точки А1,А2, …, Ап-1 , Ап такие, что их абсциссы удовлетворяют условие а <а1 <а2< …<ап-1< ап< в и выполняются условия F1 (Ап-1 )<0, F1 (Ап-1 )>0 . Тогда получим ап-1< х <ап. Если точность, с которой найдено решение, нас удовлетворяет, то можно положить х1≈ ап-1, или х1≈ ап, или х1≈ (ап-1+ап)/2. далее определяем у1 из какого-либо данного уравнения.

Заметим , что приближаться к точке А рекомендуется по любой из четырех данных дуг.

Системы, содержащие три и более уравнений, рекомендуется преобразовывать к системе с двумя уравнениями, а затем решать вышеизложенным способом. Очевидно, что такой способ проб применим для решения систем неравенств с двумя неизвестными, в этом случае способ проб дает возможность с какой угодно степенью точности указать границы областей, удовлетворяющих данной системе неравенств.

В заключении заметим, что способ проб рекомендуется сочетать с графическим методом. Графическим методом можно найти решения уравнения ( неравенства, системы) с небольшой точностью, способ проб дает возможность уточнить эти решения с какой угодно степенью точности.


Литература.

  1. Я.И. Груденов «Совершенствование методики работы учителя математики», 2002.
  2. А.М. Колдашев «Графический и численный методы решения уравнений, неравенств и их систем», 1989.