Программа профильного курса «Алгебра плюс»

Вид материала

Программа

Содержание Цели программы Задачи программы Новизна программы Ожидаемые педагогические результаты Пояснительная записка. Программа курса «Алгебра плюс» Алгебраические уравнения. – 15 ч. Рациональные алгебраические системы уравнений. - 8 ч. Алгебраические неравенства. – 5 ч. Календарно-тематическое планирование программы профильного курса «Алгебра плюс» Тема 1. Многочлены. 7 ч. Тема 2. Алгебраические уравнения. 15 ч. Тема 3. Рациональные алгебраические системы уравнений. 8 ч. Тема 4.Алгебраические неравенства. 5 ч.

Подобный материал:

• Программа элективного курса «Решение уравнений и неравенств с модулями и параметрами», 98.16kb.
• Приказ от № Рабочая программа элективного учебного предмета «Алгебра плюс: элементарная, 165.27kb.
• Программа профильного курса изучения информатики Алгоритмика, 80.96kb.
• Программа профильного курса информатики 10-11 класс пояснительная записка, 62.72kb.
• Программа по дисциплине Линейная алгебра для студентов 1 курса дневного отделения факультета, 212.1kb.
• Программа элективного курса предпрофильной подготовки и профильного обучения «Введение, 91.03kb.
• Программа элективного курса предпрофильной подготовки и профильного обучения «ссср, 149.31kb.
• Программа курса повышения квалификации учителей математики, 15.17kb.
• Программа элективного курса предпрофильной подготовки и профильного обучения «История, 160.13kb.
• Хвостёнкова Ольга Александровна п. Опытный 2004 программа курса, 84.4kb.

Программа профильного курса «Алгебра плюс»


Аннотация


Актуальность программы.


Концепция модернизации российского образования предусматривает на старшей ступени общего образования переход к профильному обучению.

Данный курс систематизирует и углубит базовые знания учащихся, позволит оптимально развить творческие способности в области математики.


Концепция представляемой программы.

В ее содержании предусмотрено:

• глубокое изучение различных методов решения алгебраических рациональных уравнений, неравенств, систем уравнений, теорем и формул, не изучаемых в традиционном школьном курсе;
  
• реальная практико-ориентированная деятельность учащихся, предоставляющая возможности: для саморазвития учащихся и для выполнения практических задач математической обработки различных процессов и явлений;
  
• блочно-модульное построение, разнообразие задание, разный уровень сложности заданий позволяет учащимся реализовать свое право на выбор заданий, соответствующих их возможностям и способностям, и взять на себя ответственность за составление своего индивидуального учебного плана.
  

Цели программы

Целью данной программы является повторение и глубокое изучение учащимися теории алгебраических рациональных уравнений, систем, неравенств, освоение разнообразных приемов практического решения, нахождение наиболее рационального решения.


Задачи программы

Развитие навыков математического анализа, приемов решения уравнений с целью нахождения наиболее рационального математически красивого решения; формирование аналитического, логического мышления, умения самостоятельной работы. Особое внимание уделяется формированию научного мировоззрения.


Новизна программы

В курс вводятся следующие теоретические и практические разделы: равносильные уравнения, метод замены переменных в дробно-рациональных уравнениях, уравнения содержащие знак модуля, уравнения с параметрами, симметрические системы уравнений, однородные системы с двумя переменными, неравенства, содержащие модули, неравенства с двумя переменными, возвратные уравнения, теорема Безу, деление многочленов.


Ожидаемые педагогические результаты:

• осознание и усвоение теорем, формул в области решения различных уравнений высших степеней дробно-рациональных уравнений, решение симметрических систем уравнений, систем с тремя переменными;
  
• усвоение различных методов решений уравнений, ознакомление с многообразием способов решения, возможностью применения их в ситуационных задачах;
  
• развитие мировоззренческого системообразующего взгляда на применение методов решения алгебраических рациональных уравнений и систем уравнений в науке;
  
• развитие умения анализа и логического, рационального подхода к решению задач.
  

Рекомендуемые методические подходы и организация занятий.

• Теоретические знания даются в виде лекций и бесед;
  
• Практическая работа в виде индивидуальных и групповых занятий.
  
• Рекомендуется давать творческие домашние задания.
  
• Проверка усвоения теоретических знаний – зачеты.
  

Содержание программы.

Программа включает в себя:

• лекций – 3 ч.
  
• бесед – 6 ч.
  
• практикум по решению задач – 14,5 ч.
  
• самостоятельных работ – 4,5 ч. (9 работ по 0,5 ч.)
  
• семинаров – 4 ч.
  
• зачетов – 3 ч.
  

Основные разделы программы:

1. Многочлены – 7 ч.

2. Алгебраические уравнения – 15 ч.

3. Рациональные алгебраические системы уравнений – 8 ч.

4. Алгебраические неравенства – 5 ч.

• Программа инвариантна т. к. включенный в программу материал может применяться для различных групп учащихся.
  
• Программа может быть разбита на несколько блоков с различным количеством часов, что достигается обобщенностью материала, модульным принципом построения.
  
• Развертывание содержания материала в программе структурировано таким образом, что изучение последующих тем, обеспечивается знанием предыдущих, а между частными и общими знаниями прослеживаются связи.
  
• Возможно, установить степень достижения промежуточных и итоговых результатов и выявить сбой в происхождении программы в любой момент процесса обучения.
  
• Во времени материал программы распределен с учетом его достаточности для качественного изучения материала и получения запланированных результатов, устранения возможных при прохождении программы сбоев.
  
• Доля практической и самостоятельной работы учащихся составляет 75%.
  
• Предусматривается продолжение изучения данного курса в 11 классе.
  
• Данная программа составлялась на основе базовой государственной программы для общеобразовательных школ, гимназий, лицеев, Математика 5- 11 кл., сост. Кузнецова Г.М. и др. Программа логически связана с программой основного курса.
  

Пояснительная записка.

Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики.

Целью данной программы является систематизация и углубление знаний по курсу алгебры. Особое внимание уделяется формированию научного мировоззрения учащихся, развитию творческих способностей.

Задачи программы: закрепление и углубление системы знаний в области математики, развитие навыков самостоятельной работы, повышение интереса к изучению математики.

Области применения программы: профильные классы средних общеобразовательных школ, лицеи, гимназии.

Возможно использование сокращенного варианта программы или отдельных тем.

Новизна программы состоит во введении в курс следующих теоретических и практических разделов: равносильные уравнения, метод замены переменных в дробно-рациональных уравнениях, уравнения содержащие знак модуля, уравнения с параметрами, симметрические системы уравнений, однородные системы с двумя переменными, неравенства содержащие модуль, неравенства с двумя переменными, возвратные уравнения, теорема Безу, деление многочленов.

Программа рассчитана на 35 ч. (1 ч. в неделю). В том числе: лекций – 3 ч.; бесед – 6 ч.; практикум по решению задач – 14,5 ч.; самостоятельных работ – 4,5 ч. (9 работ по 0,5 ч.); семинаров – 4 ч.; зачетов – 3 ч.

Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил.

Ожидаемые результаты: выработка навыков логического анализа, умения выбора рационального метода решения; развитие интереса к предмету.

Структура курса. Курс состоит из четырех разделов: многочлены - 7 ч.; алгебраические уравнения – 15 ч.; рациональные алгебраические уравнения -8 ч.; алгебраические неравенства 5 ч.

Данный курс соответствует целям и задачам профильного обучения. Курс доступен для учащихся; адаптирован, предполагает индивидуальный, дифференцированный подход.


Программа курса «Алгебра плюс»

1. Многочлены. – 7 ч.
   

Формулы (a  b)ⁿ, (a + b + c)². Делимость и деление многочленов с остатком. Теорема Безу. Корни многочленов. Общая теорема Виета.

2. Алгебраические уравнения. – 15 ч.
   

Равносильные уравнения. Следствия уравнений. Решение уравнений методом разложения на множители. Метод замены переменных при решении уравнений. Возвратные уравнения. Однородные уравнения. Дробно-рациональные уравнения. Разные способы решения. Уравнения, содержащие знак модуля. Уравнения с параметрами. Метод оценки. Использование монотонности при решении уравнений.

3. Рациональные алгебраические системы уравнений. - 8 ч.
   

Метод подстановки и метод сложения при решении систем уравнений. Решение симметрических систем уравнений. Однородные системы уравнений с двумя переменными. Замена переменных в системах уравнений. Решение системы уравнений содержащих параметры. Система с тремя переменными. Основные методы.

4. Алгебраические неравенства. – 5 ч.
   

Дробно-рациональные алгебраические неравенства. Неравенства содержащие модули. Неравенства с двумя переменными. Множество решений на координатной плоскости.


Календарно-тематическое планирование программы профильного курса «Алгебра плюс»

№	Тема урока	Форма	Основные Понятия	Оборудование	Работа учащихся	Ожидаемые результаты
Тема 1. Многочлены. 7 ч.
1.	Формулы (a ±b)n, (a + b + c)2.	Лекция , групповая работа	(a ±b)n, (a + b + c)2.	Карточки	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать; учатся работать с формулами.
2.	Формулы (a ±b)n, (a + b + c)2.	Беседа, групповая работа	(a ±b)n, (a + b + c)2	Конспект, карточки	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать; закрепление навыка работы с формулами
3.	Делимость и деление многочленов с остатком	Беседа, групповая работа	Q(x)=(x-a)·P(x)+R	Карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать
4.	Делимость и деление многочленов с остатком. Самостоятельная работа № 1.	Индивидуальная работа		Конспект, карточки	Решают задачи	Приобретается умение деления многочлена на многочлен
5.	Теорема Безу. Корни многочленов.	Беседа	Уравнение вида . Целые корни делителя an.	Карточки	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать. Формируется умение решать уравнения высших степеней.
6.	Теорема Безу. Корни многочленов. Самостоятельная работа № 2.	Индивидуальная работа		Конспект, карточки	Решают задачи	Формируется умение решать уравнения высших степеней.
7.	Общая теорема Виета.	Семинар. Групповая работа	, , ,	Конспект, карточки	Решают задачи	Знакомство с методами проверки решения уравнений с помощью теоремы Виета.
Тема 2. Алгебраические уравнения. 15 ч.
8.	Равносильные уравнения. Следствия уравнений.	Лекция. Групповая работа	Равносильные уравнения. Следствия уравнений.	Карточки	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать, Формируется умение соблюдать логическую последовательность при решении уравнений.
9.	Решение уравнений методом разложения на множители.	Беседа. Групповая работа.		Конспект, карточки	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать. Закрепляются навыки полученные на уроках алгебры.
10.	Метод замены переменных при решении уравнений. Самостоятельная работа № 3.	Групповая, индивидуальная работа		Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Закрепляются навыки полученные на уроках алгебры.
11.	Возвратные уравнения	Лекция		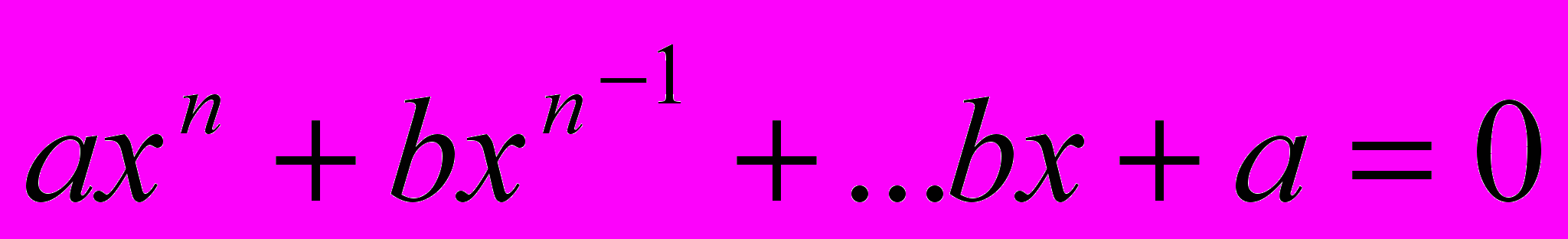Карточки	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный метод решения.
12.	Однородные уравнения. Самостоятельная работа № 4.	Групповая, индивидуальная работа		Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный метод решения.
13.	Однородные уравнения. Зачет № 1.	Индивидуальная работа		Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный метод решения.
14.	Дробно-рациональные уравнения. Разные способы решения.	Беседа. Групповая работа.		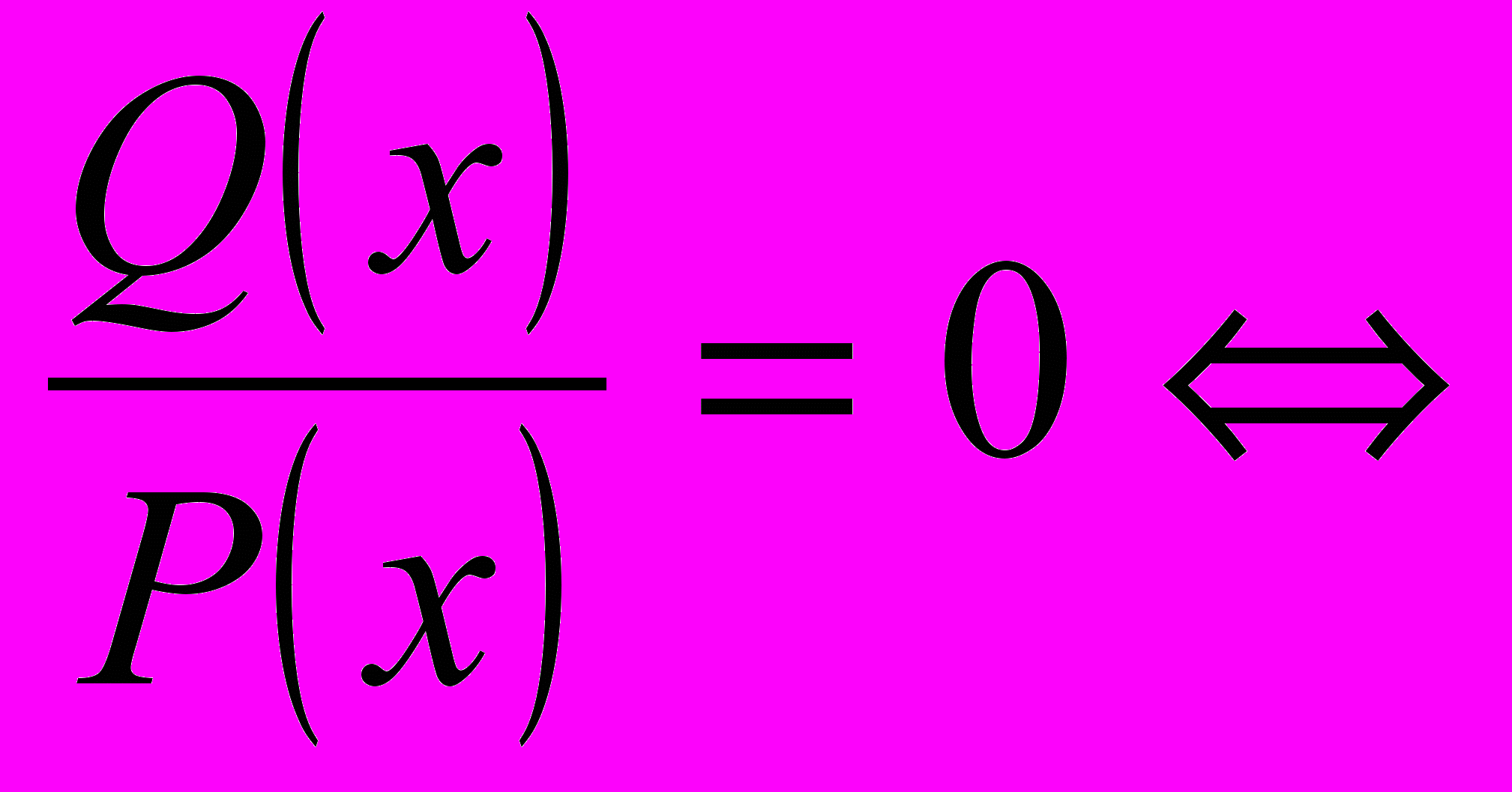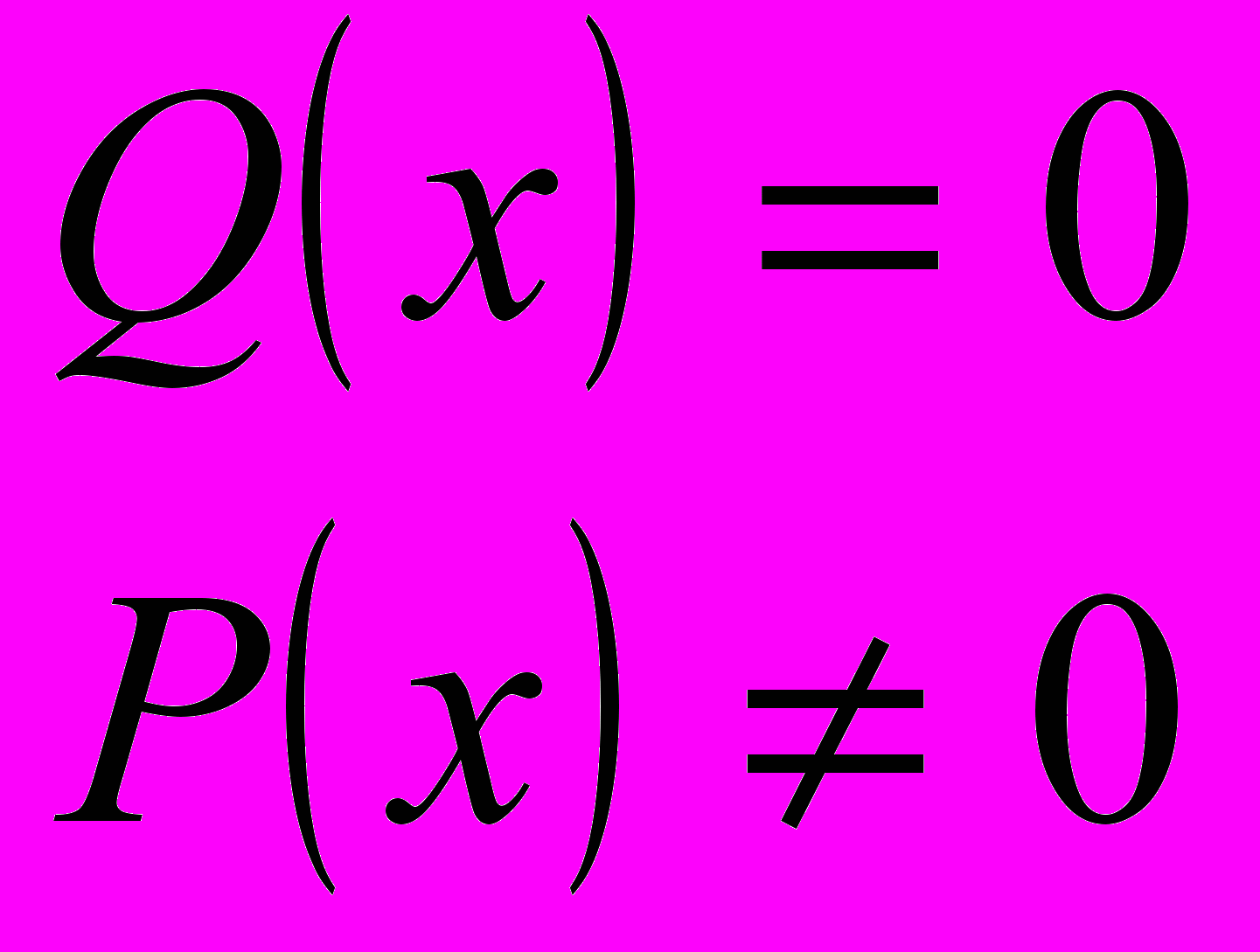Карточки	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный метод решения
15.	Дробно-рациональные уравнения. Разные способы решения.	Семинар. Групповая, индивидуальная работа.	Метод замены переменных.	Конспект, карточки.	Решают Задачи.	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный метод решения
16.	Уравнения, содержащие знак модуля.	Беседа. Групповая, индивидуальная	х при 0, IхI = -х при < 0.	Карточки.	Записывают основные понятия, решают	Вырабатывается умение логически мыслить, анализировать. Формируется умение решать уравнения, разбивая область решения на несколько.
17.	Уравнения, содержащие знак модуля. Самостоятельная работа № 5.	Групповая, индивидуальная работа		Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Формируется умение решать уравнения, разбивая область решения на несколько.
18.	Уравнения с параметрами	Беседа. Групповая, индивидуальная работа		Конспект, карточки	Решают задачи	Закрепляются теоретические знания и формируется умение их применять при решении задач.
19.	Уравнения с параметрами	Семинар. Групповая, индивидуальная работа.		Конспект, карточки.	Решают Задачи.	Закрепляются теоретические знания и формируется умение их применять при решении задач.
20.	Метод оценки. Использование монотонности при решении уравнений..	Беседа.	, , 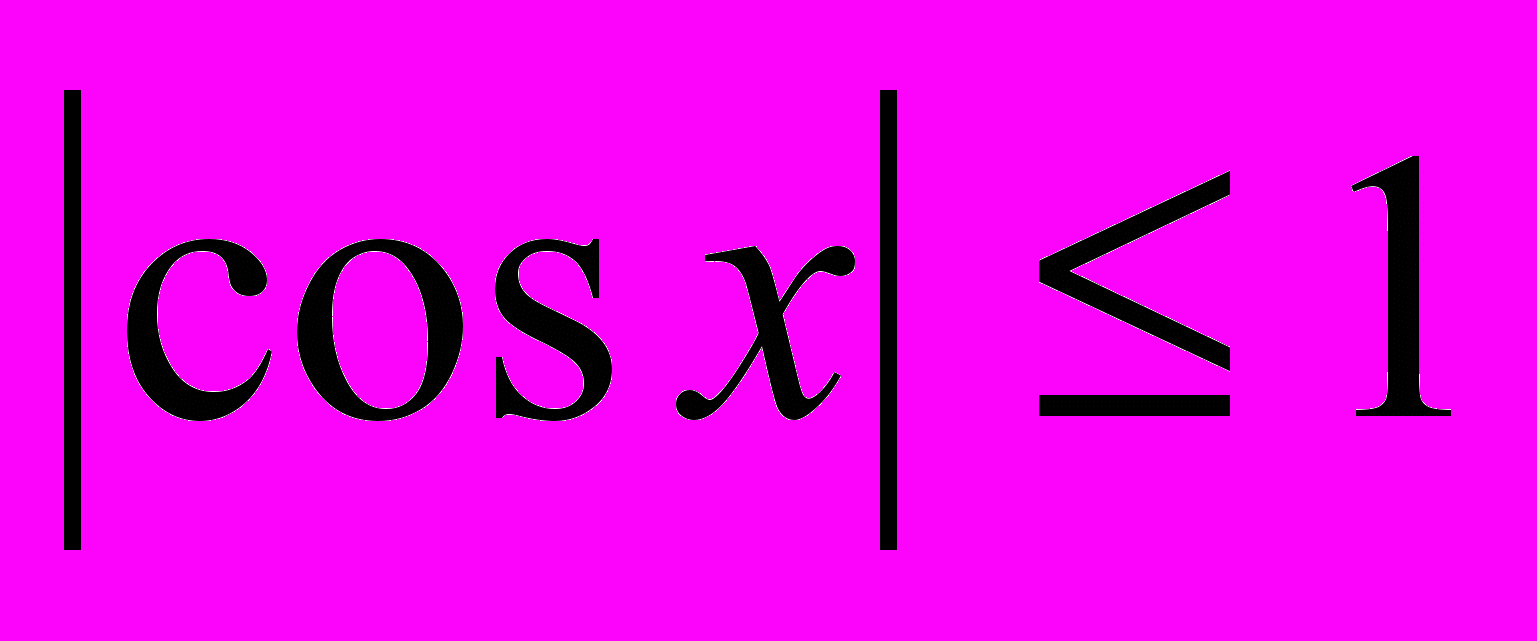, 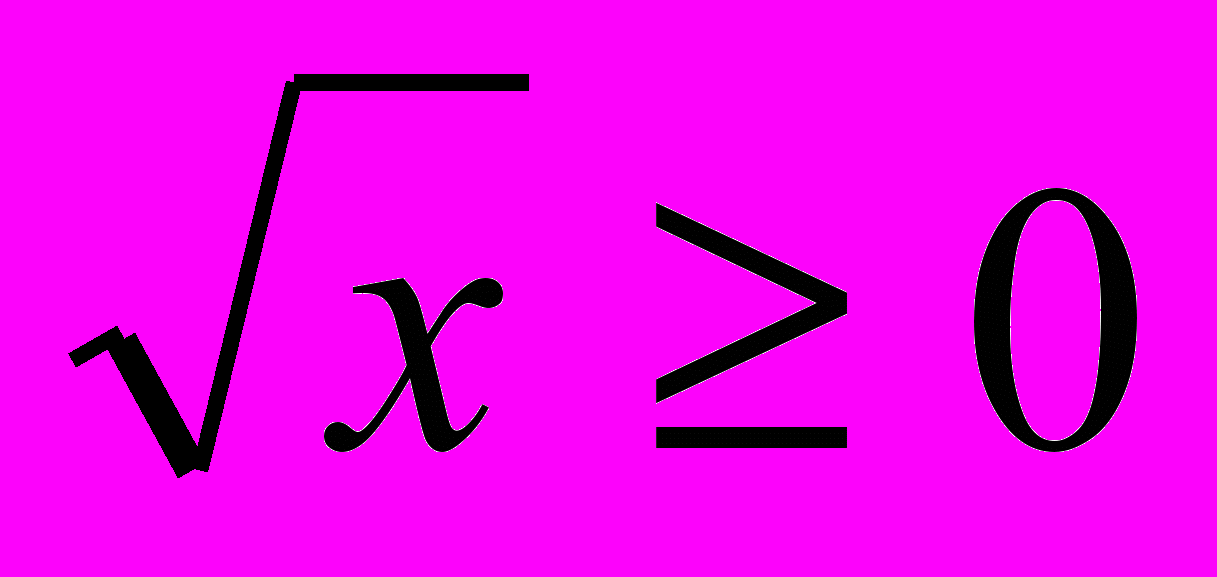. Теорема о корне	Карточки.	Записывают основные понятия, решают.	Вырабатывается умение логически мыслить, анализировать. Углубляются, систематизируются знания по теме «Свойства функций».
21.	Метод оценки. Использование монотонности при решении уравнений. Самостоятельная работа № 6.	Групповая, индивидуальная работа.		Конспект, карточки.	Решают Задачи.	Вырабатывается умение логически мыслить, анализировать. Углубляются, систематизируются знания по теме «Свойства функций».
22	Зачет № 2.	Индивидуальная работа.		Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Углубляются, систематизируются знания по теме «Алгебраические уравнения».
Тема 3. Рациональные алгебраические системы уравнений. 8 ч.
23	Метод подстановки и метод сложения при решении систем уравнений.	Беседа, индивидуальная работа.		Конспект, карточки.	Записывают основные понятия, решают.	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный способ решения систем уравнений.
24	Решение симметрических систем уравнений	Беседа, индивидуальная работа.	х + у = а, х · у = b.	Конспект, карточки.	Записывают основные понятия, решают.	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный способ решения систем уравнений.
25	Однородные системы уравнений с двумя переменными. Самостоятельная работа № 8.	Индивидуальная работа.		Конспект, карточки.	Решают задачи.	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный способ решения систем уравнений.
26	Замена переменных в системах уравнений.	Индивидуальная работа.		Конспект, карточки.	Решают задачи.	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный способ решения систем уравнений.
27.	Решение систем уравнений, содержащих параметры.	Беседа.		Конспект, карточки.	Записывают основные понятия, решают.	Вырабатывается умение логически мыслить, анализировать
28.	Решение систем уравнений, содержащих параметры.	Семинар. Групповая, индивидуальная работа		Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Формируется умение выбрать рациональный способ решения систем уравнений.
29.	Система с тремя переменными. Основные методы.	Индивидуальная работа	Метод Гаусса при решении уравнений a1x+b1y+c1z=d1 a2x+b2y+c2z=d2 a3x+b3y+c3z=d3	Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Знакомство с методом Гаусса.
30.	Система с тремя переменными. Основные методы. Самостоятельная работа № 7.	Индивидуальная работа		Конспект, карточки	Решают задачи	Вырабатывается умение логически мыслить, анализировать. Знакомство с методом Гаусса.
Тема 4.Алгебраические неравенства. 5 ч.
31.	Дробно-рациональные алгебраические неравенства	Беседа, индивидуальная работа.	Метод интервалов	Конспект, карточки.	Записывают основные понятия, решают.	Вырабатывается умение логически мыслить, анализировать. Сформировать умение пользоваться методом интервалов.
32.	Неравенства, содержащие модули	Беседа, индивидуальная работа.		Конспект, карточки.	Записывают основные понятия, решают.	Вырабатывается умение логически мыслить, анализировать. Повышение культуры работы с графиком.
33.	Неравенства с двумя переменными. Множество решений на координатной плоскости.	Беседа, индивидуальная работа.	ay  bx +c	Конспект, карточки.	Записывают основные понятия, решают.	Вырабатывается умение логически мыслить, анализировать. Повышение культуры работы с графиком.
34.	Неравенства с двумя переменными. Множество решений на координатной плоскости. Самоcтоя-тельная работа № 9.	Индивидуальная работа.		Конспект, карточки.	Решают задачи.	Углубляются знания и совершенствуются методы решения неравенств.
35.	Зачет № 3.	Индивидуальная работа.		Конспект, карточки.	Решают задачи.	Углубляются знания и совершенствуются методы решения неравенств и систем уравнений
ИТОГО:		35

Литература.

1. Виленкин Н.Я. и др. «Алгебра для 8 класса», Учебное пособие для школ и классов с углубленным изучением математики., М., «Просвещение», 1995 г.
   
2. Виленкин Н.Я. и др. «Алгебра для 9 классов», Учебное пособие для школ и классов с углубленным изучением математики., М., «Просвещение», 1996 г.
   
3. Галицкий М. Л., Мошкович М.М., Шварцбурд С.И. «Углубленное изучение курса алгебры и математического анализа.», М., «Просвещение», 1986 г.
   
4. Галицкий М. Л., Гольдман А. М., Звавич Л. И. «Сборник задач по алгебре» для 8-9классов, М., «Просвещение», 1995 т.
   
5. Говоров В.М., Дыбов П. Т. и др. «Сборник конкурсных задач по математике» М., «Наука», 1986 г.
   
6. Гусаков В. А. «Алгебра и геометрия в задачах», Краснодар, 1993 г.
   
7. Дорофеев Г. В. «Сборник заданий для проведения письменного экзамена по алгебре и началам анализа», М., «Дрофа», 2002г.
   
8. Кострикина Н.П. «Задачи повышенной трудности в курсе алгебры» 7-9 классы, М., «Просвещение», 1991 г.
   
9. Крамор В. С. «Повторяем и систематизируем курс алгебры и начал анализа», М., «Просвещение», 1990 г.
   
10. Кутасов А, Д., Пиголкина Т.С. и др. «Пособие по математике для поступающих в вузы.» М., «Наука», 1985 г.
    
11. Нестеренко Ю. В., Олехник С. Н., Потапов М.К. «Задачи вступительных экзаменов по математике», М., «Наука», 1980 г.
    
12. Мордкович А. Г. «Алгебра и начала анализа», М., «Высшая школа», 1987г.
    
13. Петров К. И. «Сборник задач по алгебре» М., «Просвещение»,1984 г.
    
14. Симонов А. Я., Бакаев Д. С. «Система тренировочных задач и упражнений по математике.», М., «Просвещение», 1991 г.
    
15. Авторский коллектив под ред. Сканави М. И. «Сборник задач для поступающих в вузы.», М., «Мир и образование», 2003 г.
    
16. Сканави М. И., «Сборник задач по математике», М. «Высшая школа», 1996 г.
    
17. Фадеев Д.К., Соминский Н. С. «Сборник задач по высшей алгебре.», М., «Наука», 1972 г.
    
18. Шарыгин И. Ф. «Факультативный курс по математике.», М., «Просвещение», 1989 г.
    
19. Шарыгин И. Ф. «Математика для поступающих в вузы.», М., «Дрофа», 1995 г.
    
20. Ястребинецкий Г. А. «Задачи с параметрами», М., «Просвещение» 1986 г.