М. К. Аммосова Кафедра математической экономики рабочая программа

Вид материала

Содержание

Недельная нагрузка : 2 ч. (лекция), 2 ч. (лаб)
Выписка из требований госстандарта
5. Принципы и цели изучения курса
2.2. Предметные цели курса.
6. Экзаменационные вопросы

Подобный материал:

Министерство образования Российской Федерации

Якутский государственный университет

имени М.К. Аммосова

Кафедра математической экономики

РАБОЧАЯ ПРОГРАММА

ДИСЦИПЛИНЫ

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ

И МЕТОДЫ ОПТИМИЗАЦИИ

по направлению 510100 « математика »

2003 г.

Составитель Н.К.Алексеев - профессор кафедры математической экономики.

3. В Ы П И С К А И З У Ч Е Б Н О Г О П Л А Н А

Всего часов: 110 ч.

В том числе аудиторных занятий: 72 ч.

самостоятельной работы: 38 ч.

Курс «Вариационное исчисление и методы оптимизации» изучается по направлению 510100 – математика в течение одного семестра.

Недельная нагрузка : 2 ч. (лекция), 2 ч. (лаб)

Виды занятий	Семестр 7
Аудиторные	72
Лекционные Лабораторные	36 36
Самостоятельная работа	38
Итого	110
Форма контроля	экзамен

ВЫПИСКА ИЗ ТРЕБОВАНИЙ ГОССТАНДАРТА

Требования (федеральный компонент) к обязательному минимуму содержания и уровню подготовки бакалавра и дипломированного специалиста по циклу «Общие математические и естественнонаучные дисциплины».

Требования к знаниям и умением по циклу «Общие математические и естественнонаучные дисциплины».

Требования к образованности бакалавра математических, естественнонаучных и сельскохозяйственных направлений высшего профессионального образования.

После освоения математических и естественнонаучных дисциплин бакалавр должен иметь представления:

об основных математических структурах и методах;
о математическом моделировании;
об информации, способах её хранения, обработки и представления;

Бакалавр должен знать и уметь использовать в области математики:

- методы математического анализа;
- методы алгебры, геометрии;

методы теории дифференциальных уравнений и математической физики;

1.4 - методы численного эксперимента;

1.5 - методы теории вероятностей и математической статистики.

ОПД.Ф.16 110

Элементы дифференциального исчисления и выпуклого анализа; гладкие задачи с ограничениями типа равенств и неравенств; правило множителей Лагранжа; задачи линейного программирования и проблемы экономики; теорема двойственности; классическое вариационное исчисление; уравнение Эйлера; условия второго порядка Лежандра и Якоби; задачи классического вариационного исчисления с ограничениями; необходимые условия в изопериметрической задаче и задаче со старшими производными; классическое вариационное исчисление и естествознание; оптимальное управление; принцип максимума Понтрягина; оптимальное управление и задачи техники; методы решения задач линейного программирования; симплекс-метод; методы решения задач без ограничения; градиентные методы; метод Ньютона; методы сопряженных направлений; численные методы решения задач вариационного исчисления и оптимального управления.

5. ПРИНЦИПЫ И ЦЕЛИ ИЗУЧЕНИЯ КУРСА

2.1. Принципы построения программы.

- Рабочая программа соответствует Государственному образовательному стандарту высшего и профессионального образования по направлению 510100 – математика.

- Курс имеет как теоретическую, так и практическую направленность.

2.2. Предметные цели курса.

После изучения дисциплины студент должен иметь представление:

О месте и роли экстремальных задач в математике и в приложениях, связанных с оптимизацией различных процессов, происходящих в экономике, в технике, в народном хозяйстве, в экологии, в военном деле и т.д.;
Об основах линейного, нелинейного, выпуклого программирования, об оптимальном управлении и динамическом программировании, о численных методах оптимизации.

Студент должен знать и уметь использовать:

2.2.1 - методы минимизации функций многих переменных с ограничениями типа равенств и неравенств;

-градиентные методы спуска;

2.2.3 - методы выпуклого программирования;

2.2.4 - методы линейного программирования;

2.2.5 - применение правила множителей Лагранжа для решения задач нелинейного программирования;

2.2.6 - необходимые и достаточные условия экстремума функционала при решении задач классического вариационного исчисления;

2.2.7 - принцип максимума Л.С.Понтрягина при решении задач оптимального управления;

2.2.8 - метод динамического программирования и принцип оптимальности Р.Беллмана для решения задач оптимального управления.

Интеллектуальные цели

2.2.9 - умение формулировать задачу и ставить цель;

2.2.10 – приобретение склонности к творческой деятельности;

2.2.11 - приобретение навыков самостоятельной работы над изучением учебно-методической и научной литературы по данному курсу и его приложениям;

- мение видеть и решать нестандартные задачи.

6. ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ

1. Понятие о задачах оптимизации. Постановка задачи нелинейного программирования (НЛП). Общая схема решения задач НЛП. Классификация методов решения задач НЛП.

2. Выпуклые оболочки, выпуклые множества, выпуклые функции. Леммы о выпуклых функциях. Критерии выпуклости функций. Геометрическая иллюстрация.

3. Условия экстремума. Необходимые условия 1-го и 2-го порядков. Теоремы о необходимых и достаточных условиях.

4. Существование, единственность, устойчивость точки минимума. Теорема Вейерштрасса о существовании решения. Понятие невырожденной и локально-единственной точки минимума. Теорема, связывающая локально-устойчивую и локально-единственную точки минимума. Понятие глобально-устойчивой точки минимума. Теорема о глобально-устойчивой точке минимума.

Понятие слабо устойчивого множества точек глобального минимума. Условия слабой устойчивости множества точек глобального минимума.

5. Понятие о безусловной минимизации функций многих переменных. Градиентный метод. Формулировка теорем о сходимости. Метод скорейшего спуска. Формулировка теорем о сходимости.

6. Методы 2-го порядка в задачах безусловной оптимизации. Поиск минимума без вычисления производных, метод Гаусса-Зейделя.

7. Минимизация функций на выпуклых множествах. Теорема о множестве точек локального минимума выпуклых функций на выпуклых множествах. Теорема о необходимом условии минимума дифференцируемой функции на выпуклом множестве. Теорема о необходимом и достаточном условиях минимума выпуклой функции на выпуклом множестве.

8. Понятие проекции точки на множество, оператора проектирования, расстояния точки до множества. Лемма о свойствах проекции на выпуклое замкнутое множество.

9. Теорема о необходимом условии минимума дифференцируемой функции на выпуклом множестве, формулируемом с помощью проекции. Теорема о необходимом и достаточном условиях минимума выпуклой функции на выпуклом множестве, формулируемом с помощью проекции.

10. Метод условного градиента минимизации дифференцируемой функции на выпуклом, замкнутом, ограниченном множестве. Формулировка теоремы о сходимости метода условного градиента для случая выпуклой функции.

11. Метод проекции градиента для минимизации дифференцируемой функции на выпуклом, замкнутом, ограниченном множестве. Условный метод Ньютона.

12. Задачи НЛП с ограничениями типа равенств. Метод исключения. Правило множителей Лагранжа. Теорема об обосновании правила множителей Лагранжа. Уточненная формулировка правила множителей Лагранжа. Утверждение о нормальных точках минимума. Нормальное правило множителей Лагранжа. Формулировка правила множителей для анормальных задач.

13. Задачи линейного программирования(ЛП). Постановка. Геометрическая интерпретация. Решение задач ЛП графическим методом. Понятие опорного плана, базиса, базисных, вне базисных переменных. Модифицированный симплекс метод ( метод обратных матриц). Мультипликативное представление обратной матрицы.

14. Постановка задач вариационного исчисления. Типы функционалов. Понятие линейного нормированного пространства, функционала, примеры. Понятие линейного, непрерывного функционала, примеры. Понятие относительного минимума функционала, вариации функционала. Теорема об относительном экстремуме функционала. Понятие стационарной точки, линейного многообразия, примеры. Основная лемма вариационного исчисления. Функционалы вида:

F(y)=

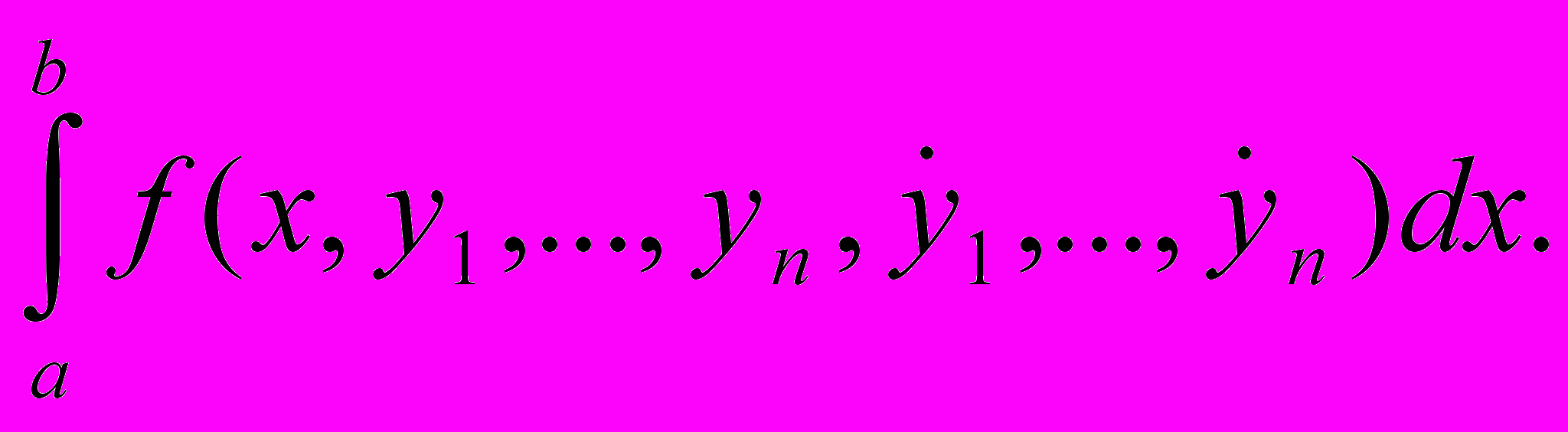
Первая вариация. Уравнение Эйлера. Функционалы вида

F(y)=

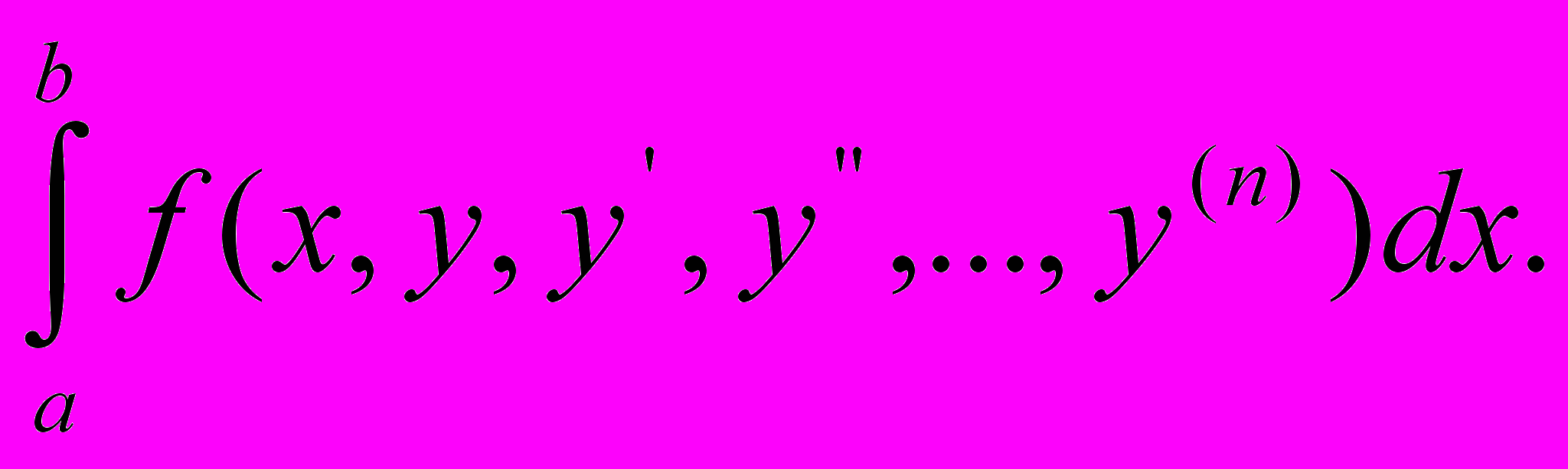
Первая вариация. Уравнения Эйлера.

15. Достаточные условия экстремума функционала. Понятие дифференцируемого функционала. Связь между производной функционала и первой вариацией. Понятие дважды дифференцируемого функционала. Формулировка достаточного условия относительного экстремума. Достаточное условие Вейерштрасса для функционала

F(y)=

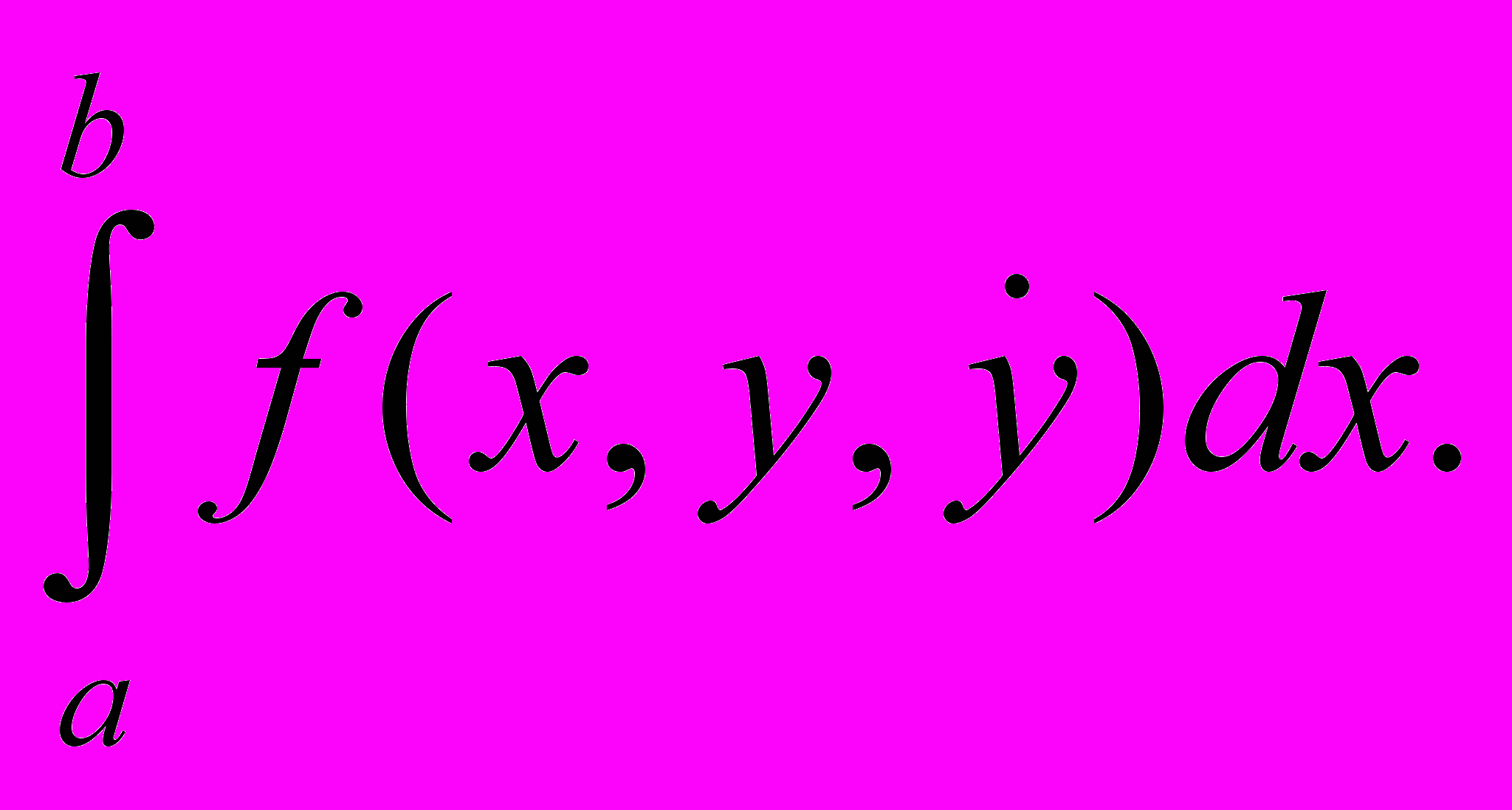
. Условный экстремум. Формулировка теорем об условном экстремуме.

16. Постановка задач оптимального управления. Фазовые и управляющие переменные. Амплитудные ограничения, примеры. Интегральные ограничения, примеры.

17. Интерпретация решения системы дифференциальных уравнений при заданном кусочно-непрерывном управлении. Частные случаи уравнений движения обьекта.

Критерии качества управления. Типы критериев качества.
Классификация задач оптимального управления по типу ограничений на фазовые пе-

ременные.

Распространенные задачи оптимального управления. Основные проблемы теории

управляемых процессов.

Принцип максимума Л.С. Понтрягина в теории оптимальных систем.
Применение принципа максимума, как проверочного условия. Применение принципа

максимума для выявления структуры оптимального управления.

Применение принципа максимума для сведения задачи оптимального управления к

решению двухточечной краевой задачи

Дифференциальный принцип максимума. Принцип максимума для случая открытой

области управления.

Принцип максимума для задач Больца, Лагранжа.
Принцип максимума для задач терминального управления с нефиксированной продолжительностью процесса.

27. Свойства функции Гамильтона. Достаточность принципа максимума для линейных систем.

28. Интегральный принцип максимума. Теоремы о необходимости и достаточности интегрального принципа максимума.

29. Методы последовательных приближений на основе принципа максимума.

ЛИТЕРАТУРА

Основная

1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М. 2000.

2. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе, Мищенко. Математическая теория оптимальных процессов. М.: Наука, 1978.

3. Акулич И.Л. Математическое программирование в примерах и задачах. М. Выс.шк., 1986.

4. Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. М,: Наука, 1984.