Менеджмента качества положение о модульно-рейтинговой системе квалиметрии учебной деятельности студентов
| Вид материала | Документы |
| Алтайский государственный технический университет им. И.И.Ползунова Учебное пособие 3 График контроля 4 Шкала оценок и правила вычисления рейтинга 5 Возможности повышения рейтинга |
- Положение о модульно-рейтинговой системе оценки знаний студента I. Рейтинговая оценка, 90.36kb.
- Удк 387. 14 Вопросы менеджмента качества образования, 6.15kb.
- Положение распространяется на штатных преподавателей, занимающих должность профессора, 100.38kb.
- Методические рекомендации по организации учебного процесса с использованием модульно-рейтинговой, 554.48kb.
- Облем, связанных с переходом к компетентностному формату образовательных программ,, 208.9kb.
- Методическое руководство по модульной системе обучения и рейтинговой оценке деятельности, 479.93kb.
- Методическое руководство по модульной системе обучения и рейтинговой оценке деятельности, 116.64kb.
- Задачи : организация качественного перехода на фгос спо обеспечение своевременности, 77.67kb.
- И. М. Губкина Кафедра «Техническая механика» Положение о рейтинговой системе оценки, 59.48kb.
- Практические (семинарские) занятия описание рейтинговой системы, 768.19kb.
Алтайский государственный технический университет им. И.И.Ползунова
Памятка для студентов групп ПОВТ 31-34 по изучению дисциплины «Математический анализ» (3 семестр)
Составил ________________ Утверждаю
Зав. кафедрой ___________
« » ___________200_ года
1 Содержание дисциплины
В 3 семестре продолжается изучение дисциплины «Математический анализ». Будут рассмотрены следующие темы.
Модуль 1. ТЕМА 5. Функции нескольких переменных.
Евклидово n-мерное пространство. Открытые и замкнутые множества. Предел последовательности точек пространства. Теорема Больцано-Вейерштрасса. Понятия предельной точки, компактного и связного множества.
Предел и непрерывность функции нескольких переменных. Свойства непрерывных функций. Свойства функций, непрерывных на компактном множестве.
Частные производные и дифференцируемость функции. Дифференциал 1 порядка, его свойства. Частные производные и дифференциалы высших порядков. Формула Тейлора. Необходимые и достаточные условия экстремума. Неявные функции, их существование и дифференцирование. Условные экстремумы, метод множителей Лагранжа.
Геометрические вопросы теории функций нескольких переменных: понятие скалярного поля, поверхности и линии уровня, производная поля по направлению, градиент, касательная плоскость и нормаль к поверхности.
Модуль 2. ТЕМА 6. Кратные, криволинейные, поверхностные интегралы.
Мера Жордана. Определение и свойства кратных интегралов. Вычисление двойных интегралов в декартовых координатах. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах. Тройной интеграл в декартовой, цилиндрической, сферической системах координат.
Криволинейные интегралы 1 рода: определение, свойства, вычисление. Понятие площади поверхности. Поверхностные интегралы 1 рода. Приложения интегралов в геометрии и механике.
ТЕМА 7. Элементы теории векторных полей.
Криволинейные интегралы 2 рода. Условия независимости от пути интегрирования. Формула Грина. Ориентация поверхности. Поверхностные интегралы 2 рода. Формула Гаусса-Остроградского. Теорема Стокса.
Понятие векторного поля. Потенциальные поля, условия потенциальности. Поток, дивергенция, циркуляция, ротор векторного поля. Соленоидальные и гармонические векторные поля. Операторы Гамильтона и Лапласа.
Модуль 3. ТЕМА 8. Числовые ряды.
Понятие числового ряда. Свойства сходящихся рядов. Критерий Коши. Признаки сходимости (признаки сравнения, Даламбера, Коши, интегральный). Теорема Лейбница. Абсолютная и условная сходимость.
ТЕМА 9. Функциональные последовательности и ряды.
Поточечная и равномерная сходимость. Область сходимости. Сумма ряда. Критерий Коши и признак Вейерштрасса равномерной сходимости. Непрерывность суммы. Почленное дифференцирование и интегрирование функциональных рядов.
Степенные ряды. Теорема Абеля. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд. Приложения степенных рядов.
ТЕМА 10. Ряды Фурье, интеграл и преобразование Фурье.
Гармонические колебания. Ортогональность тригонометрической системы функций. Понятие ряда Фурье. Разложение функций в ряд Фурье. Приближение функций алгебраическими и тригонометрическими многочленами. Свойство минимальности коэффициентов Фурье. Неравенство Бесселя, равенство Парсеваля.
Абстрактные ряды Фурье в гильбертовом пространстве (понятие гильбертова пространства, сходимость по норме, ряд Фурье по ортонормированной системе функций, свойство минимальности коэффициентов Фурье, неравенство Бесселя, полные системы функций).
Комплексная форма ряда Фурье. Интеграл и преобразование Фурье.
Литература и учебно-методические материалы
(более полный список – у преподавателя)
- Берман Г.Н. Сборник задач по курсу математического анализа–М.: Наука, 1985.–383 с.
- Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление – М.: Наука, 1988. – 432 с.
- Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного – М.: Наука, 1989 г. -464 с.
- Кудрявцев Л.Д. Курс математического анализа. В 3 т. – М.: Высш.шк., 1988. – Т.1 – 712 с., Т.2 – 575 с., Т.3. – 351 с.
- Пискунов Н.С. Дифференциальное и интегральное исчисления. В 2 т. – М.: Наука, 1985.– Т.1 – 432 с., Т.2 – 576 с.
- Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. Функции нескольких переменных – М.: Высш.шк., 1988 г. - 288 с.
Учебное пособие
- Киркинский А.С. Математический анализ: Учебное пособие. Часть 2.- 2-е изд., перераб. - Алт. гос. техн. ун-т им. И.И.Ползунова. Центр дистанционного обучения. Барнаул: Изд-во АлтГТУ, 2003 г.-234с. (продается в ЦДО).
3 График контроля
| Модуль | Контрольное испытание | Время проведения | Вес в итоговом рейтинге | Примечания |
| 1 | Контрольная работа по теме 5 | 5 неделя | 0,1 | 5 задач |
| Коллоквиум по теме 5 | 6 неделя | 0,1 | 1 основной вопрос (55 баллов), 3 дополни-тельных (по 15 баллов) | |
| 2 | Индивидуальные домашние зада-ния по темам 6, 7 | 10 неделя | - | Оцениваются по принципу зачтено/не зачтено |
| Контрольная работа по теме 7 | 11 неделя | 0,1 | 4 задачи | |
| 3 | Контрольная работа по теме 8 | 13 неделя | 0,1 | 8 задач |
| Контрольная работа по темам 9, 10 | 16 неделя | 0,1 | 4 задачи | |
| Экзамен (по темам 6 – 10) | Сессия | 0,5 | 2 вопроса по 40 баллов, 2 – по 10 баллов | |
Примечания. 1. Любая контрольная точка, выполненная после срока без уважительной причины, оценивается на 10% ниже. Максимальная оценка в этом случае 90 баллов.
2. К экзамену допускаются студенты, имеющие не более двух задолжностей по контрольным точкам. При наличии одной или двух задолжностей студенту на экзамене выдаётся дополнительное задание.
3. «Автоматы» по математическому анализу не выставляются.
4 Шкала оценок и правила вычисления рейтинга
В АлтГТУ принята 100-балльная шкала оценок. Именно эти оценки учитываются при подсчёте рейтингов, назначении стипендии и в других случаях. Традиционная шкала будет использоваться только в зачётных книжках. Соответствие оценок устанавливается следующим образом: 75 баллов и выше – «отлично», 50 – 74 балла – «хорошо», 25 – 49 баллов – «удовлетворительно», менее 25 баллов – «неудовлетворительно».
Успеваемость студента оценивается с помощью текущего рейтинга (во время каждой аттестации) и итогового рейтинга (после сессии). Во всех случаях рейтинг вычисляется по формуле:
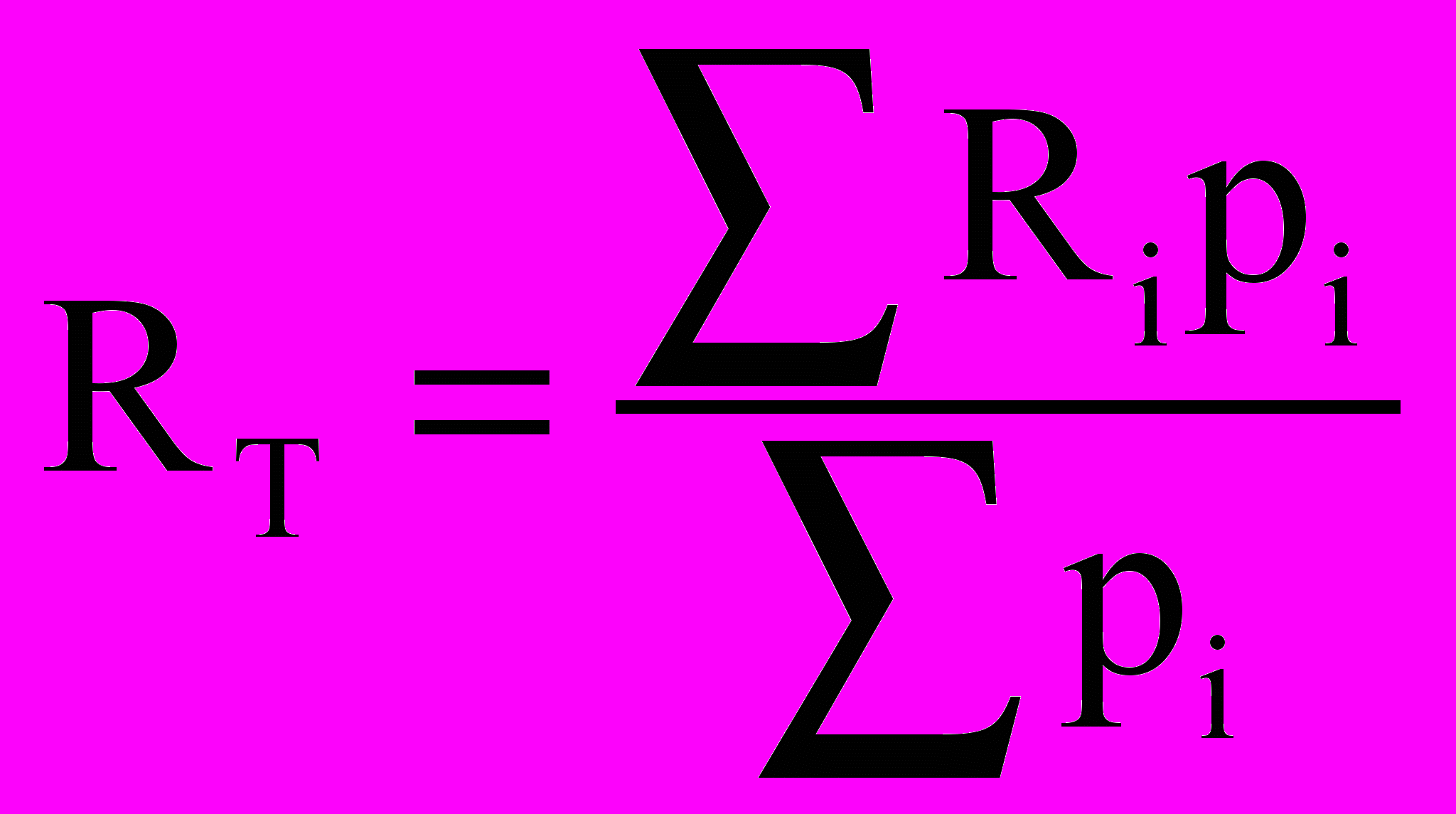 ,
,где Ri – оценка за i-ю контрольную точку, pi – вес этой контрольной точки. Суммирование проводится по всем контрольным точкам с начала семестра до момента вычисления рейтинга.
Приведём пример. Пусть студент Сидоров Иван Петрович получил следующие оценки. Контрольная работа по теме 5 – 38 баллов, коллоквиум – 60, индивидуальные задания выполнены, контрольная работа по теме 7 – 32 балла, контрольная работа по теме 8 – 80, контрольная работа по темам 9, 10 – 58, оценка за ответ на экзамене – 70 баллов. На 1-й аттестации (7 неделя) его рейтинг равен:
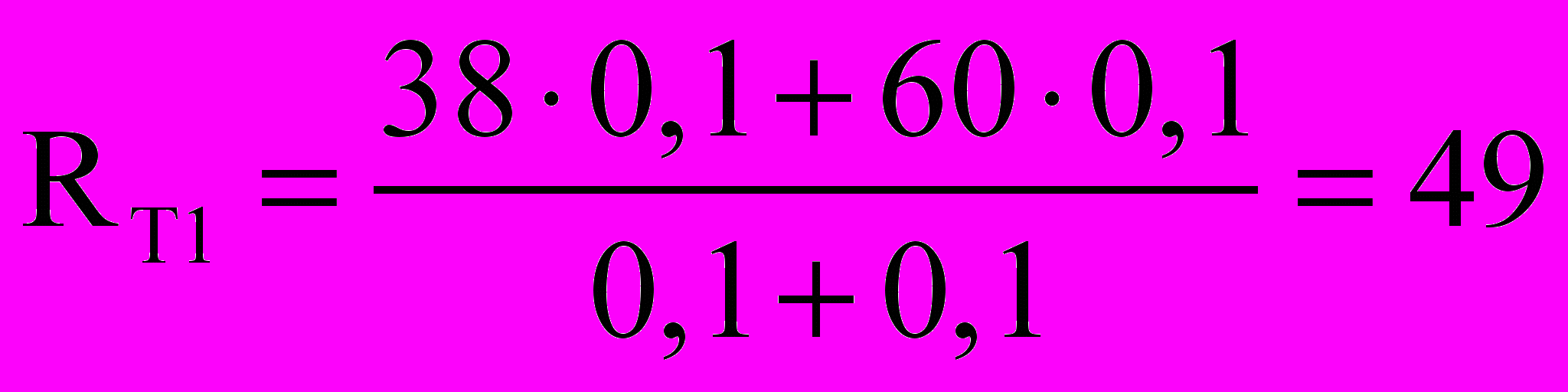 .
.На 2-й аттестации (13 неделя):
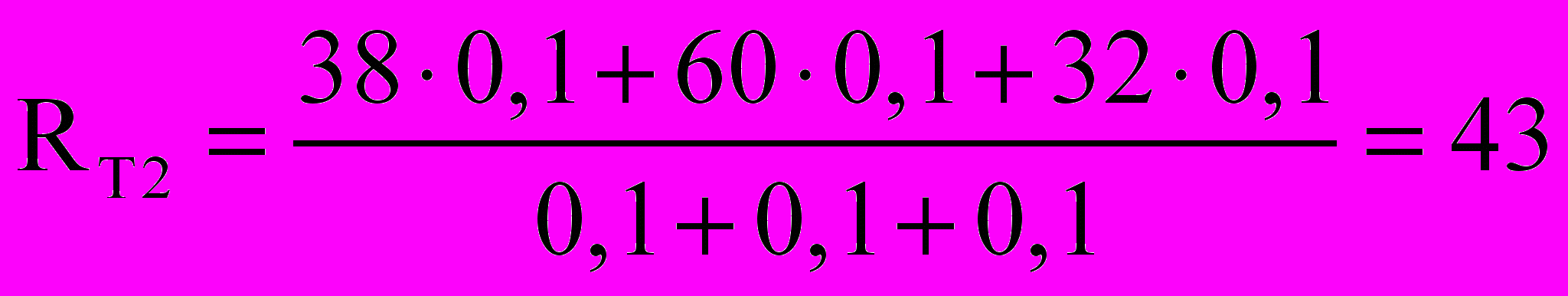 .
.Перед началом сессии вычисляется семетровый рейтинг:
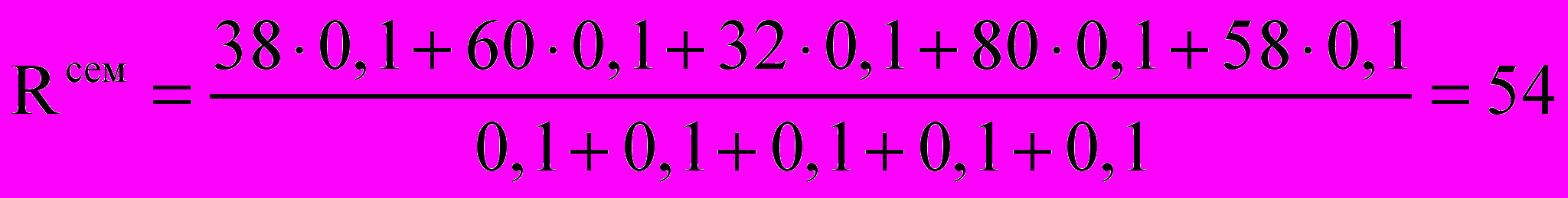 .
.Итоговый рейтинг, учитывающий экзамен:
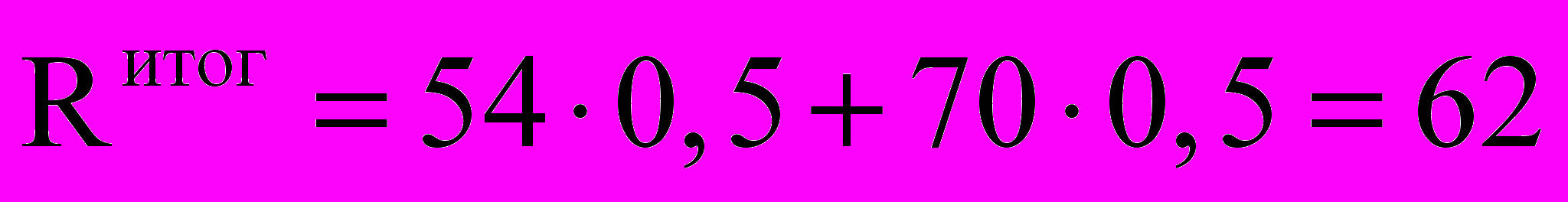 .
.В зачётку выставляется оценка «хорошо».
5 Возможности повышения рейтинга
Для студентов с высоким текущим рейтингом по их желанию может быть организовано углубленное изучение предмета, выдано дополнительное задание. В этом случае проводится дополнительный контроль: либо решение задач (контрольная работа, олимпиада), либо защита реферата. После проведения такого контроля (с оценкой R* ), текущий рейтинг пересчитывается:
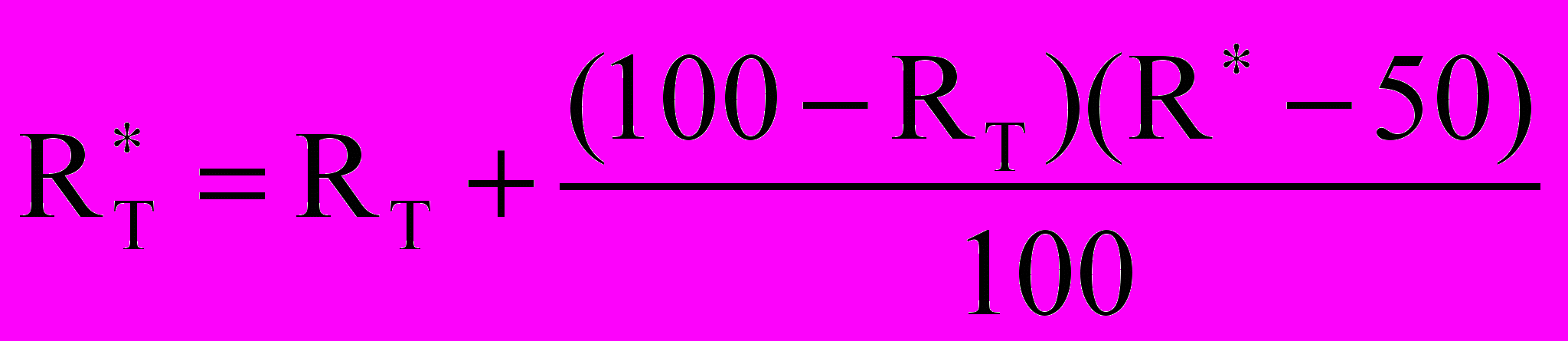 .
.Деканат, учитывая рейтинги студента по каждой дисциплине, вычисляет комплексные рейтинги, вывешивает рейтинг-листы специальности, курса, факультета.
