Методические указания к лабораторным работам по курсу "Математическое моделирование и применение ЭВМ в химической технологии " (часть 2) для студентов 4 курса химико-технологического факультета / Сост.
| Вид материала | Методические указания |
- Методические указания к электронным лабораторным работам по курсу физической химии, 2388.82kb.
- Работам по курсу «Математическое моделирование и проектирование» для студентов магистратуры, 262.63kb.
- И математическое моделирование, 1392.77kb.
- Методические указания к лабораторным работам по физике по практикуму «Вычислительная, 138.12kb.
- Методические указания к лабораторной работе по курсу "Базы данных", 114.06kb.
- Методические указания к лабораторным работам по курсу, 438.32kb.
- Методические указания к лабораторным работам по биологической химии для студентов, 948.06kb.
- Методические указания по лабораторным работам Факультет: электроэнергетический, 554.73kb.
- Методические указания к лабораторным работам для студентов специальности 210100 "Автоматика, 536.56kb.
- Методические указания к лабораторным работам №1-5 для студентов специальности 210100, 363.6kb.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
ОДЕССКИЙ НАЦИОНАЛЬНЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Химико – технологический факультет
М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
к лабораторным работам по курсу
"Методы прогрнозорования состояния окружающей среды"
для студентов химико-технологического факультета
по специальностям:
7.091601 ХИМИЧЕСКАЯ ТЕХНОЛОГИЯ ОРГАНИЧЕСКИХ ВЕЩЕСТВ
7.091602 ХИМИЧЕСКАЯ ТЕХНОЛОГИЯ НЕОРГАНИЧЕСКИХ ВЕЩЕСТВ
7.070801 ЭКОЛОГИЯ
Часть 2
Разработали: доц.кафедры ТООС Луговской В. И.
доц. кафедры ТНВ Брем В.В.
г. Одесса 2003
Методические указания к лабораторным работам по курсу "Математическое моделирование и применение ЭВМ в химической технологии " (часть 2) для студентов 4 курса химико-технологического факультета / Сост. В.И.Луговской, В.В.Брем. – Одесса: ОНПУ, 2003.- 56 с.
| Составители | доц. кафедры ОФТ, к.т.н. Луговськой В.И. доц. кафедры ТНВЕ, к.х.н. Брем В.В. доц. кафед |
Утверждено методической комиссией
химико-технологического факультета ОНПУ
Зарегистрировано в лаборатории информационных технологий ОНПУ
МВ-469 № 977-РС-2003
Скопировано с оригинал-макета, предоставленного авторами
CОДЕРЖАНИЕ
Лабораторная работа N 10 …………………………………….......................…. 3
Лабораторная работа N 11 …………………………………….......................…. 13
Лабораторная работа N 12 ..…………………………………….................…..... 18
Лабораторная работа N 13 ........................……………………………………… 22
Лабораторная работа N 14 .........................……………………………………… 29
Лабораторная работа N 15 .........................……………………………………… 35
Лабораторная работа N 16 .........................……………………………………… 40
Литература, рекомендуемая при подготовке к лабораторным работам ..............42
Лабораторная работа 10
"Исследование устойчивости Реактора"
Цель работы – при заданных значениях параметров процесса. провести анализ устойчивости реактора идеального смешения:
– определить число и характер стационарных режимов;
– исследовать статические и динамические характеристики по каналам: температура - температура входа; температура параметр теплоотвода; температура - адиабатический разогрев;
– определить условия существования единственного низко- или высокотемпературного режима;
I. Постановка задачи.
Не любое состояние химической системы, рассчитанное по математической модели, реализуется в практических условиях. Причиной этого является то, что ни один реальный реактор не работает в строго стационарном режиме. Флуктуации состава исходной смеси, колебания внешний условий и другие малые случайные возмущения непрерывно выводят процесс из стационарного состояния. Очевидно, что процесс может протекать нормально только в том случае, если малые внешние воздействия приводят к малым отклонениям режима процесса от стационарного; в противном случае любое слабое неконтролируемое возмущение приведет к нарастающему удалению от заданного стационарного состояния, т.е. к срыву процесса.
Если система, выведенная каким-либо малым внешним воздействием из стационарного состояния, после прекращения действия возмущающего фактора возвращается в первоначальное состояние, то данное стационарное состояние называется устойчивым. На практике реализуются лишь устойчивые состояния. Исследование вопросов устойчивости будет рассмотрено на примере реактора идеального смешения - простейшей из систем, исследуемых в теории химических реакторов. В режиме идеального смешения значения всех переменных одинаковы по всему объему реактора. В соответствии с этим стационарный режим реакторов такого типа описывается алгебраическими, а нестационарные - обыкновенными дифференциальными уравнениями. Исследование их устойчивости осуществляется наиболее просто.
При протекании экзотермической реакции в реакторе идеального смешения возможно существование нескольких стационарных режимов, одни из которых являются устойчивыми, другие - неустойчивыми. Число стационарных режимов и их характер определяется совокупностью значений параметров процесса.
2. Описание методики выполнения работы
Анализ устойчивости реактора идеального смешения удобно проводить с использованием диаграммы интенсивности тепловыделения и теплоотвода. Для ее построения и дальнейшего анализа необходимо выполнить следующие этапы:
1) Привести имеющиеся параметры н безразмерному виду;
2) Выполнить необходимые расчеты, построить диаграмму "тепловыделение-теплоотвод" для номинального режима и определить число и характер стационарных режимов;
3) Построить линии тепловыделения и теплоотвода при варьировании следующих параметров - температуры входа, параметра теплоотвода и адиабатического разогрева и определить статические характеристики реактора идеального смешения по каналам;
4) Определить условия существования единственного низко- или высокотемпературного режима;
5) Найти условия, при которых промежуточный режим может быть устойчивым я оценить реалистичность этих условий;
6) Построить динамические характеристики реактора идеального смешения и провести их анализ,
2.1. Приведение модели РИС к безразмерному виду
Поведение объекта определяется совокупностью значений параметров, входящих в математическое описание. Проведем классификацию параметров модели РИС.
Входные параметры:
| - технологические: | Твх , Свх , Qвх , Тх * |
| - конструктивные: | V, S* |
| - теплофизические: | a, Сp , r, СA * |
| - параметры, характеризующие реакцию: | ( -DH), Е, В. |
Выходные параметры:
| - технологические: | Твых , С* |
| - время: | t. |
Для нахождения всего трех выходных параметров необходимо задать 13 входных параметров. Для упрощения исследования модели и сокращения количества параметров применяют запись уравнений модели в безразмерной форме. Вводятся ряд безразмерных параметров (табл. 1).
Таблица 1
После подстановки безразмерных параметров и преобразований получаем модель РИС в безразмерном виде:
- Материальный баланс:
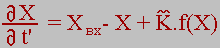 | (2.1) |
- Энергетический баланс:
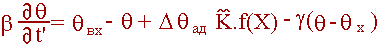 | (2.2) |
- Уравнение кинетики:
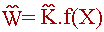 | (2.3) |
где :
 | |
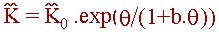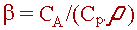 | отношение усредненной теплоемкости аппарата к теплоемкости реакционной смеси ("безразмерная теплоемкость") |
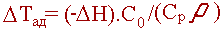 | адиабатический разогрев, т.е. величина, характеризующая на сколько градусов разогреется реакционная смесь при полной степени превращения |
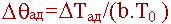 | адиабатический разогрев в безразмерной форме |
 | безразмерный параметр теплоотвода |
| b=R*T0/E | критерий Аррейниуса |
 | константа скорости реакции при опорной температуре |
| X | степень превращения |
| T0 | опорная температура, K; |
| R | газовая постоянная |
 | время пребывания (контакта) |
| C0 | концентрация на входе |
| n | порядок реакции |
Подсчитаем количество параметров в безразмерной модели:
а) выходные параметры:
- технологические
- время t'
б) входные параметры:
- технологические Хвх ,
в) теплофизические -
, 
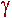. г) параметры характеризующие реакцию -
, b, 
. В безразмерной модели 8 параметров. Таким образом число параметров сократилось за счет исчезновения конструктивных параметров. Это является важным достоинством безразмерной модели РИС.
2.2. Построение Q-T-диаграммы и исследование устойчивости стационарных режимов РИС
Одной из основных характеристик химического реактора является его устойчивость, т.е. способность возвращаться к исходному стационарному состоянию после устранения внешних возмущений.
Для исследования устойчивости РИС широко используют диаграмму зависимости тепловыделения и теплоотвода от температуры (Q-T-диаграмму).
Вначале рассмотрим зависимость скорости реакции, протекающей в РИС на примере единственной необратимой реакции 1-го порядка.
Скорость реакции в размерном виде выражается следующей зависимостью:
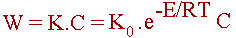 | (2.4) |
Значение концентрации C в реакторе зависит от величины концентрации на входе C 0 и температуры в реакторе T. Из уравнения материального баланса для стационарного режима следует, что:
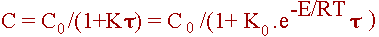 | (2.5) |
где = V/Q - время контакта, с.
Подставив (2.5) в (2.4), окончательно получим:
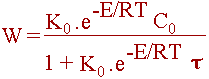 | (2.6) |
Г
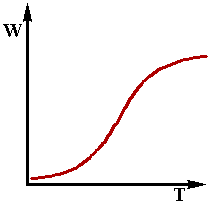рафик зависимости (2.6) имеет следующий вид (см.рис. 2.1):При малых значениях температуры Т второе слагаемое в знаменателе пренебрежимо мало по сравнению с едининицей.
Тогда:
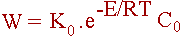(2.7)В этой области с повышением температуры
скорость реакции растет по закону Аррейниуса Рис.2.1 (нижняя ветвь графика).
При больших температурах, наоборот, второе слагаемое в знаменателе формулы (2.6) становится много больше единицы.
Тогда :
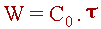 | (2.8) |
где τ= V/Q - время контакта.
Физический смысл зависимости (2.8) достаточно ясен. При высоких температурах реакция протекает настолько быстро, что реагирует практически все вещество, поступающее в аппарат. В этом режиме скорость реакции W практически не зависит от температуры (верхняя ветвь графика).
Аналогичный вид имеет эти зависимости и в безразмерной форме.
Для построения Q - T - диаграммы рассмотрим уравнение энергетического баланса в безразмерной форме (2.2). В стационарном режиме накопление тепла равно нулю. Запишем уравнение энергетического баланса в следующем виде:
 | (2.9) |
Обозначим левую часть уравнения qR - выделение тепла, т.е. количество тепла, выделяемого при протекании химической реакции в единицу времени, а правую - qT - отвод тепла, т.е. количество тепла, отводимого в единицу времени через стенку холодильника и с потоком.
В стационарном режимве выделение и отвод тепла равны между собой - qR=qT
Преобразуем выражение для расчета величины теплоотвода qT :
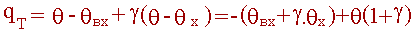
Окончательно:
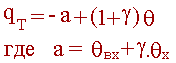 | (2.10) |
Выражение для расчета величины тепловыделения qR :
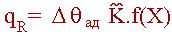 | (2.11) |
Характер зависимостей (2.10) и (2.11) от температуры следующий. Выражение (2.10) представляет собой уравнение прямой линии, причем qT растет с увеличением
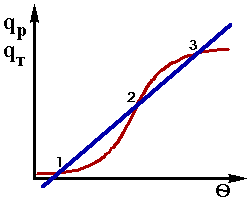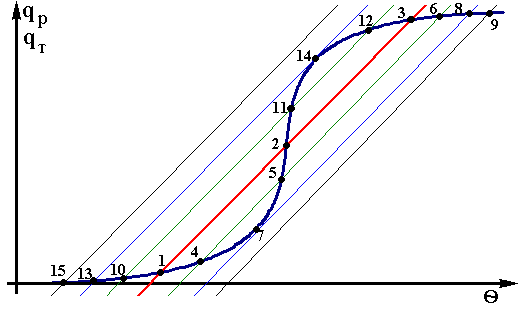
асштабом (рис.2.2). Линии зависимостей qR и qT от температуры пересекаются в трех точках-1,2 и 3. В этих точках при температурах
d
Как видно из графика (рис.2.2) в данной ситуации при одних и тех же значениях входных параметров возможны три различных стационарных режима, не Рис.2.2 только обеспечивающие различные значения выходных
параметров, но и отличающиеся по устойчивости.
Рассмотрим вначале стационарный режим 3, который соответствует режиму работы при температуре
В точке 3 линия теплоотвода проходит с большим углом наклона, чем линия тепловыделения. Поэтому при температуре
Таким образом, стационарный режим в точке 3 возвращается к исходному состоянию после снятия внешних возмущений, т.е. режим устойчивый.
Способность системы (реактора) возвращаться к исходному стационарному состоянию после снятия возмущений называется устойчивостью. Иначе говоря, исходный стационарный режим устойчив, если после устранения источников нарушения режима любые малые отклонения с течением времени стремятся к нулю. Если же значения отклонений нарастают во времени, то исходный стационарный режим неустойчив.
При температуре
Теперь рассмотрим режим в точке 2. Здесь наклон линии теплоотвода меньше, чем линии тепловыделения. Но так же, как и в точках 1 и 3, qR=qT, и если нет возмущений, режим будет стационарным. Пусть произошло случайное возмущение и температура
Проведенный анализ показал, что из трех возможных в данных условиях стационарных режимов только два: 1-при низкой температуре (и, соответственно, малой скорости реакции) и 3-при высокой температуре (и большой скорости реакции) являются устойчивыми, а третий - при промежуточных значениях температуры и скорости реакции (точка 2) - неустойчив.
2.3. Влияние входных параметров на стационарные режимы.
Построение статических характеристик РИС
Рассмотрим влияние изменения основных параметров на входе в РИС на стационарные режимы.
Скорость теплоотвода является функцией следующих параметров:
qT = f(θвх θх γ) (2.12)
Поскольку уравнение зависимости скорости теплоотвода от параметров (2.10) представляет собой уравнение прямой линии, то при изменении параметров, входящих в коэффициент a - θвх и θх, линия теплоотвода будет перемещаться параллельно самой себе.
Рассмотрим влияние температуры входа на стационарные режимы. При увеличении θвх линия теплоотвода будет смещаться вправо. При этом условия существования стационарных режимов будут другими. На рис.2.3 показаны линии теплоотвода, построенные при разных значениях
