Методические указания к лабораторным работам по курсу "Математическое моделирование и применение ЭВМ в химической технологии " (часть 2) для студентов 4 курса химико-технологического факультета / Сост.
| Вид материала | Методические указания |
- Методические указания к электронным лабораторным работам по курсу физической химии, 2388.82kb.
- Работам по курсу «Математическое моделирование и проектирование» для студентов магистратуры, 262.63kb.
- И математическое моделирование, 1392.77kb.
- Методические указания к лабораторным работам по физике по практикуму «Вычислительная, 138.12kb.
- Методические указания к лабораторной работе по курсу "Базы данных", 114.06kb.
- Методические указания к лабораторным работам по курсу, 438.32kb.
- Методические указания к лабораторным работам по биологической химии для студентов, 948.06kb.
- Методические указания по лабораторным работам Факультет: электроэнергетический, 554.73kb.
- Методические указания к лабораторным работам для студентов специальности 210100 "Автоматика, 536.56kb.
- Методические указания к лабораторным работам №1-5 для студентов специальности 210100, 363.6kb.
Рис.3. Блок-схема метода наискорейшего спуска
2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Работа выполняется в такой последовательности:
- для расчета целевой функции используют процедуру – подпрограмму "KRI0PT"
(см. лабораторную работу №5);
- для расчета частных производным по независимым переменным составляют и транслируют подпрограмму-процедуру "PROlZ";
- Выполняют расчеты на ЭВМ по программе "МBRAD" (реализующей
метод градиента) и по программе "НAIСКОР" (реализующей
метод наискорейшего спуска), в результате которых определяют координаты точки экстремума целевой функции;
- осуществляют проверку - является ли найденный экстремум глобальным, для чего расчеты повторяется несколько раз из начальных точек с различными координатами.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
В лабораторной работе №5 (табл. 5.1) приведены целевые функции и
область допустимых изменений исследуемых независимых переменных.
Требуемая точность определения координат точки экстремума 0,001.
ОФОРМЛЕНИЕ ПРОТОКОЛА
В протоколе по лабораторной работе описываются результаты расчётов, выполненных на ЭВМ, приводятся доказательства нахождение глобального экстремума.
Кроме того, в протокол включается листинг подпрограммы, и распечатки расчетов.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Классификация методов решения задач оптимизации.
2. Общая идея методов нелинейного программирования.
3. Метод градиента, алгоритм расчета.
4. Блок-схема метода градиента.
5. Метод наискорейшего спуска, алгоритм расчета.
6. Блок-схема метода наискорейшего спуска.
7. Методы поиска экстремума функции одной переменной.
8. Как доказать, что найденный экстремум является глобальным?
Лабораторная работа 16
Использование методов линейного программирования
для решения оптимизационных задач
ЦЕЛЬ РАБОТЫ: – определить экстремум целевой функции с использованием симплекс– метода данцига
- Описание методики расчетов
Линейное программирование представляет собой математический аппарат, разработанный для решения оптимизационных задач с линейным выражением для критерия оптимальности и линейными ограничениями на область изменения переменных.
Математически задача линейного программирования формулируется следующим образам.
Имеется ряд переменных Х1, Х2, …Хn . Требуется найти такие неотрицательные значения этих переменных, которые бы удовлетворяли системе линейных уравнений (ограничениям)
а11X1 + а12X2 + … + а1nXn ≥ В1
а21X1 + а22X2 + … + а2nXn ≥ В2 (1)
…………………………………
аm1X1 + аm2X2 + … + аmnXn ≥ Вm
и, кроме того, линейная функция достигала экстремума.
R = C1X1 + C2X2 + … + CnXn (2)
В системе (1) могут быть как равенства, так и неравенства.
Для решения таких задач используется симплекс–метод данцига
Пусть система ограничений (1) записана в виде равенств. Полагая, что ранг матрицы коэффициентов меньше числа неизвестных, выразим r неизвестных системы (1) через остальные:
X1 =
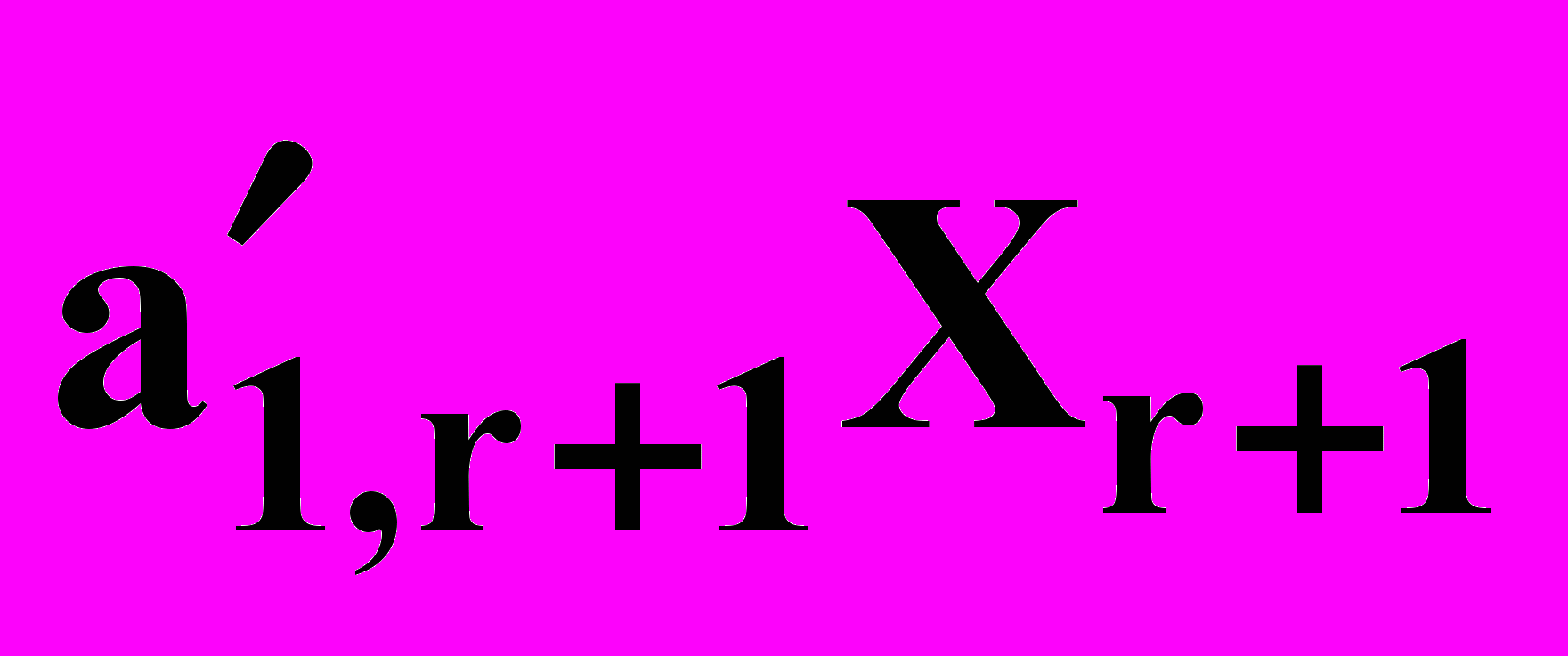 +
+ 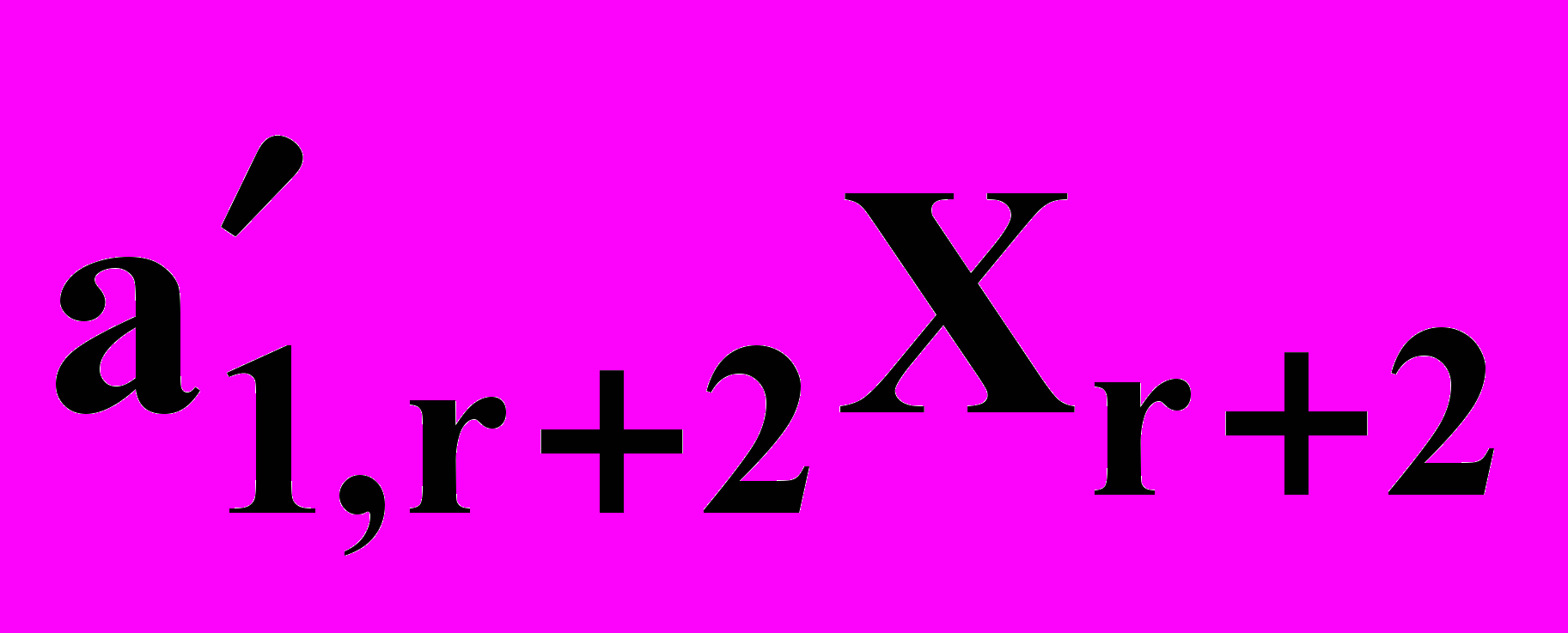 + …+
+ …+  +
+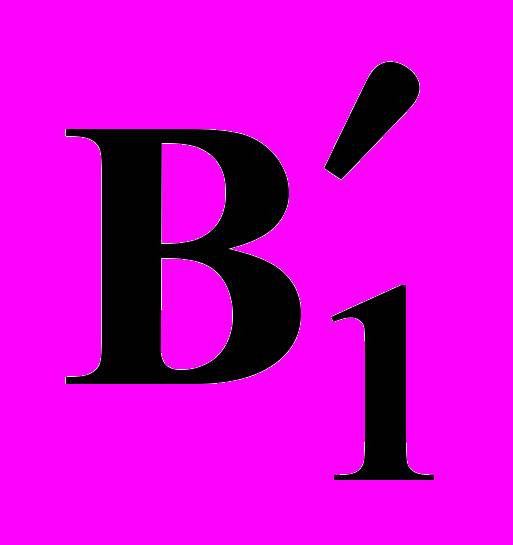
X2 =
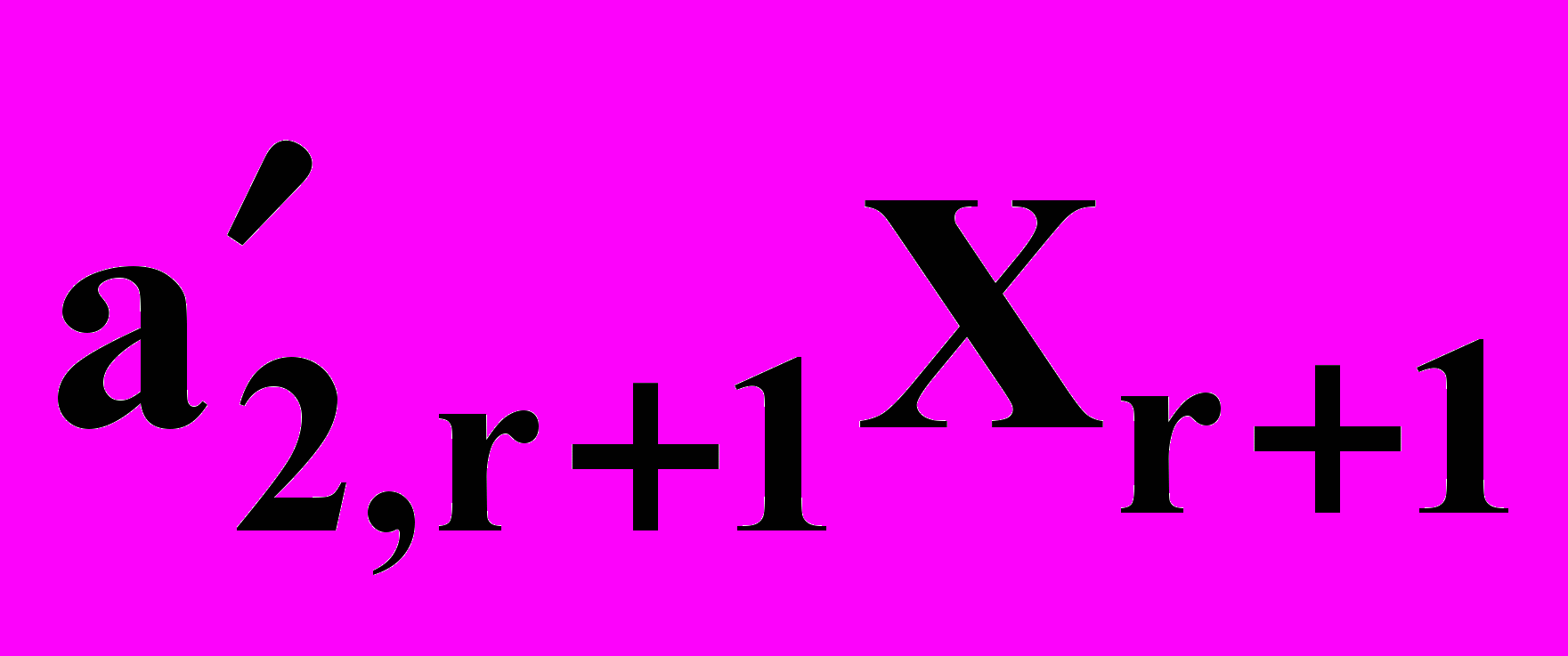 +
+ 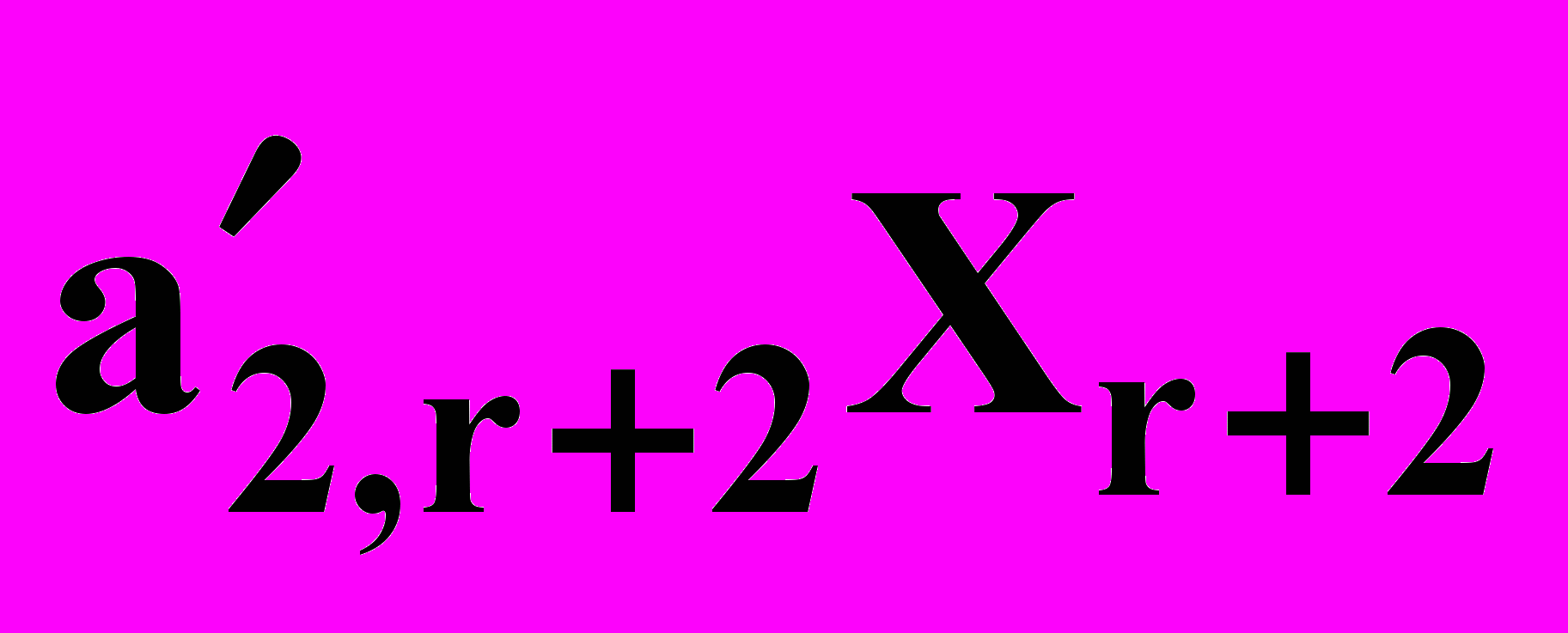 + …+
+ …+ 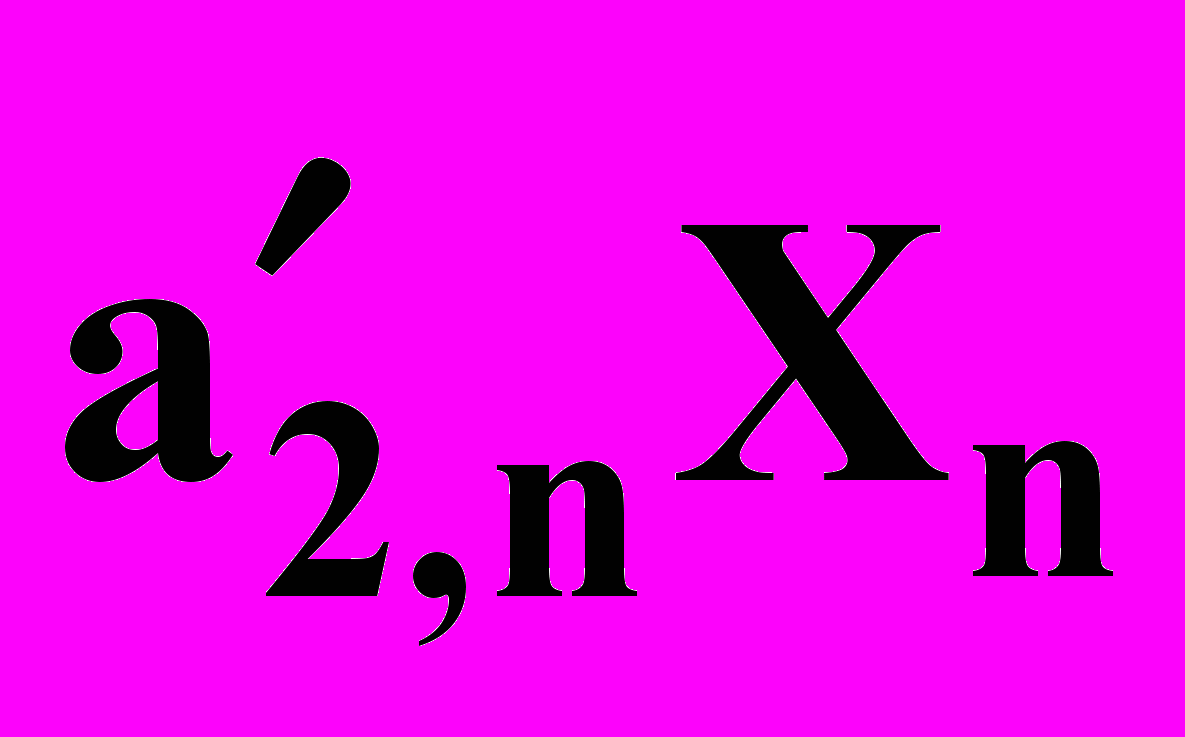 +
+ 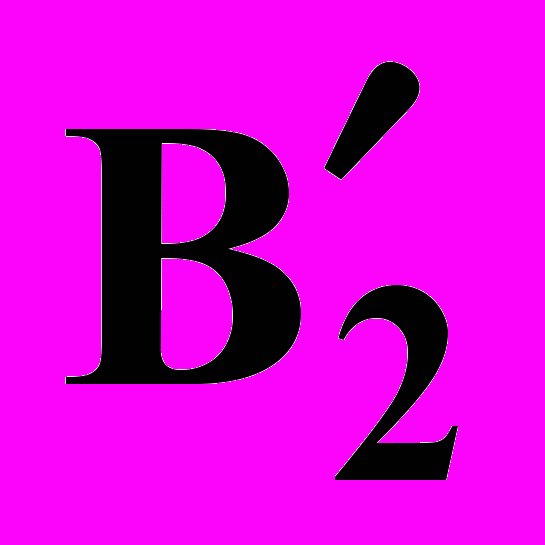 (3)
(3)…………………………………
Xr =
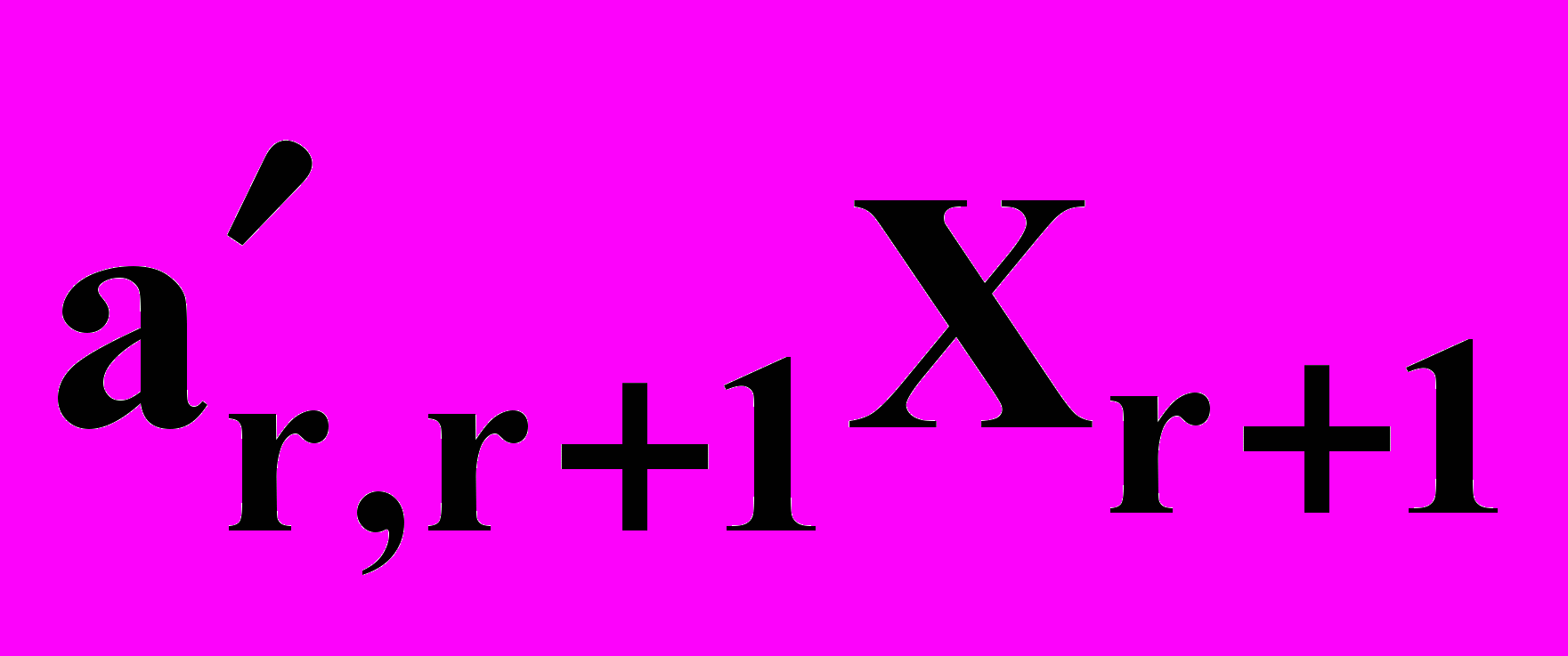 +
+ 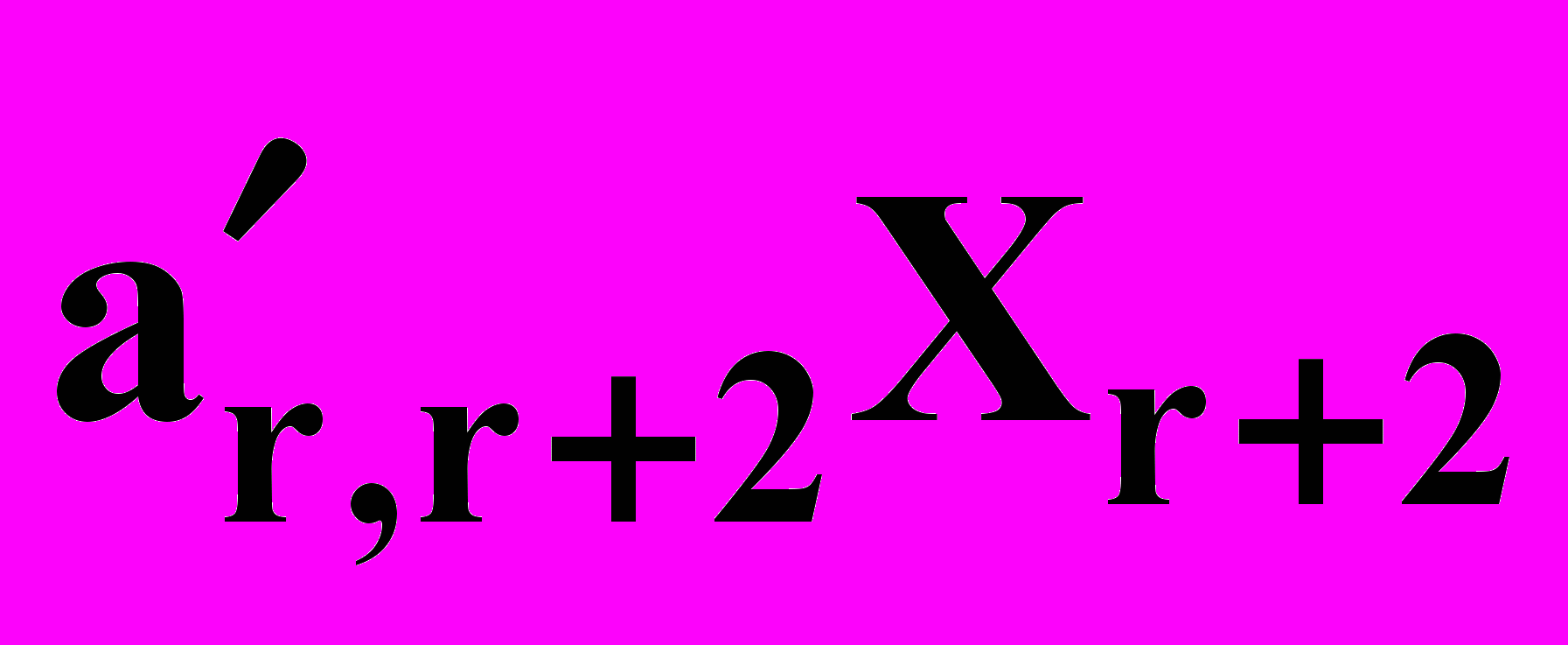 + …+
+ …+ 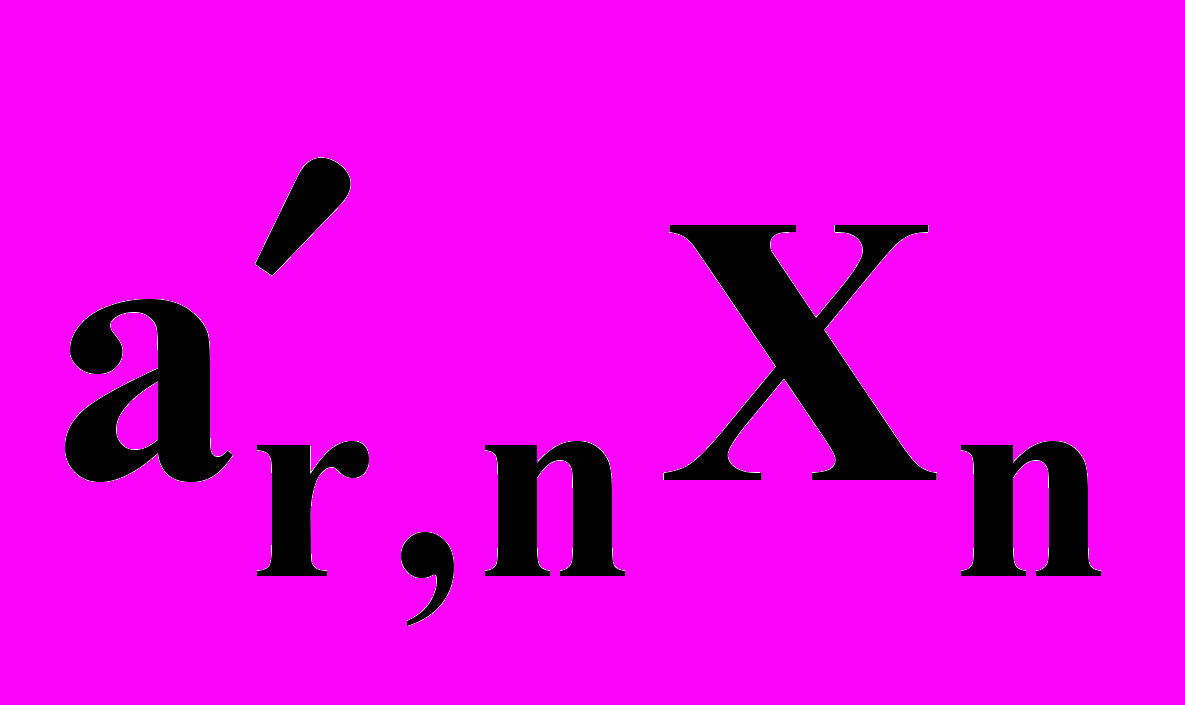 +
+ 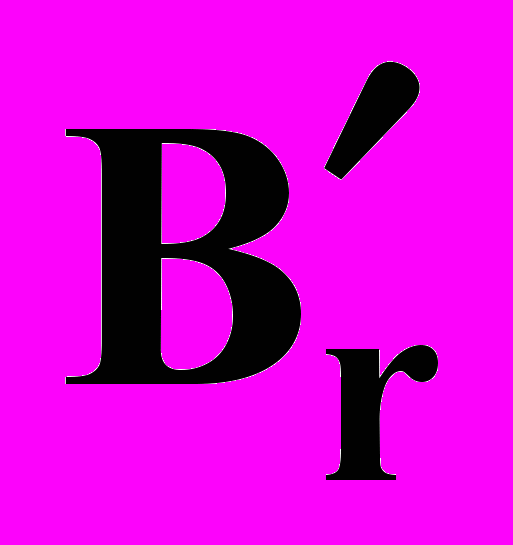
Неизвестные Х1, Х2, …Хr называются базисными, остальные переменные – свободные.
Т.к. свободным неизвестным можно придавать любые неотрицательные значения (Xr+1 ≥ 0), то свободные члены
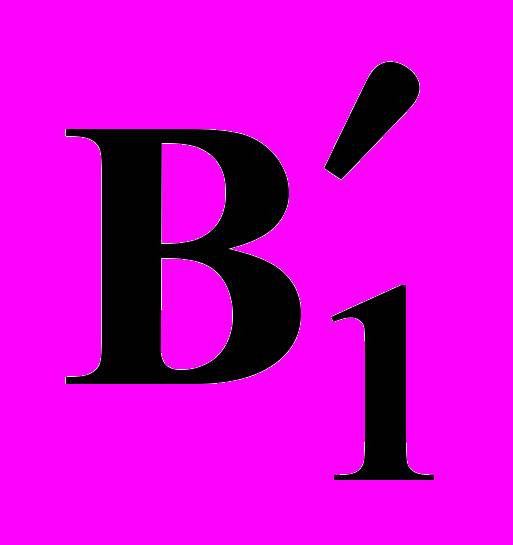 ,
, 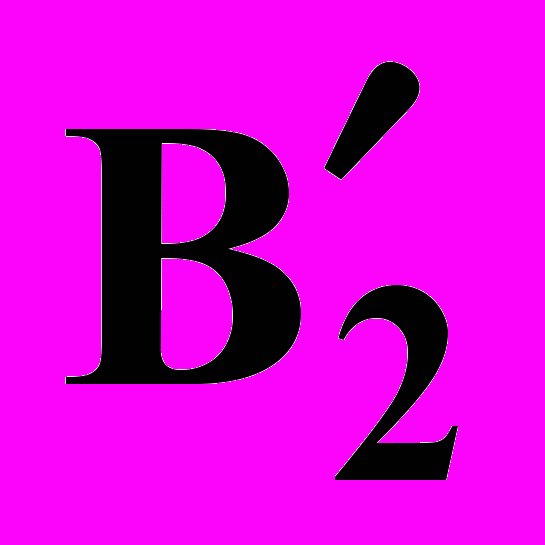 , …,
, …, 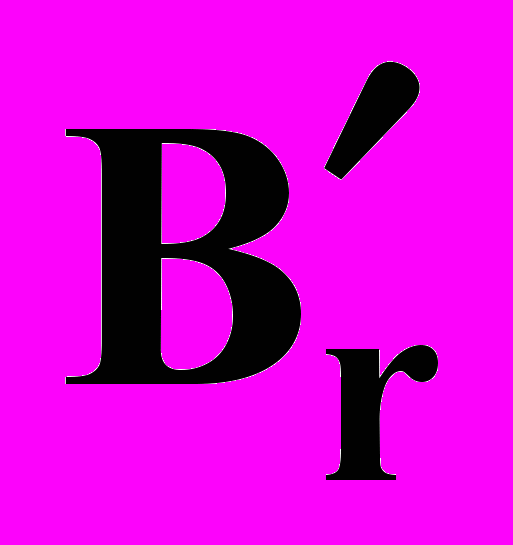 должны быть положительными, поскольку в противном случае (т.е. если
должны быть положительными, поскольку в противном случае (т.е. если  <0 при Xr+1= 0; Xr+2= 0; … Xn = 0) получим Хj <0 (j=1, 2,…, r).
<0 при Xr+1= 0; Xr+2= 0; … Xn = 0) получим Хj <0 (j=1, 2,…, r).Положив все свободные неизвестные равными 0 (Xr+1= 0; Xr+2= 0; … Xn = 0) получим:
Х1=
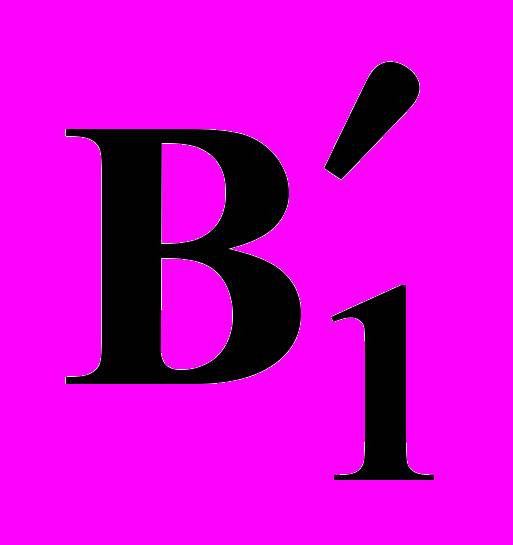 ; Х2=
; Х2=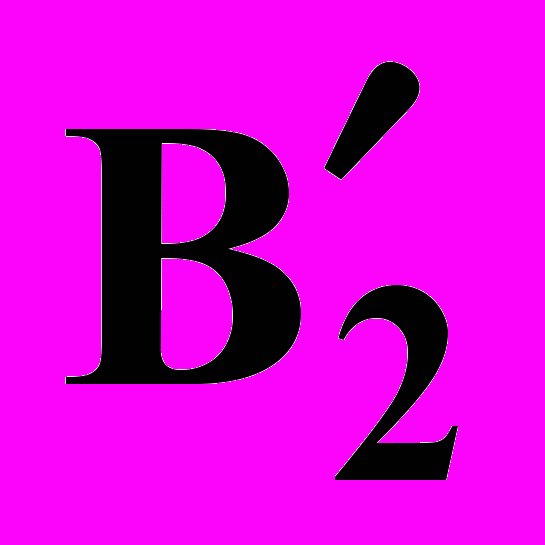 … Хr =
… Хr = 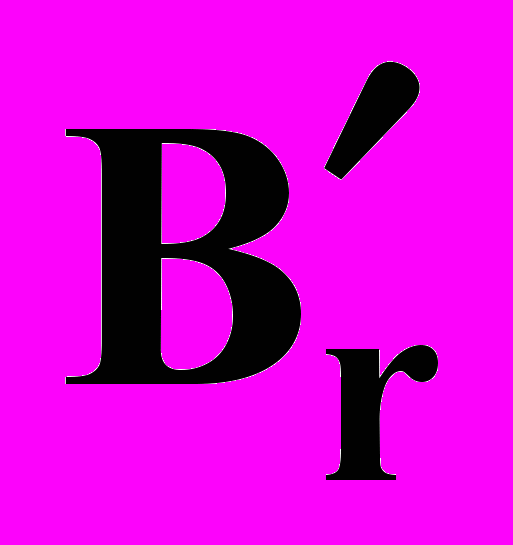 (4)
(4)При этом вектор (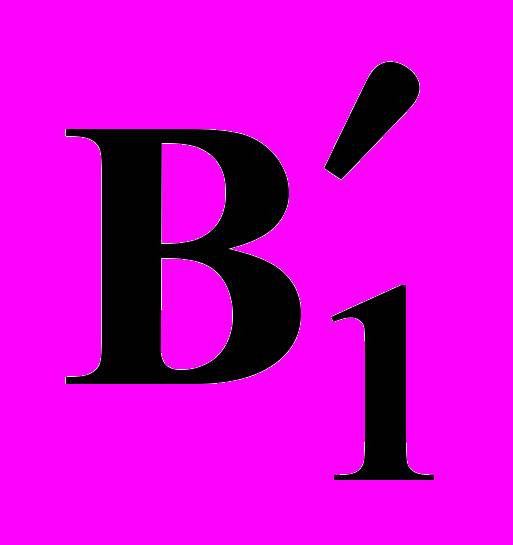 ,
, 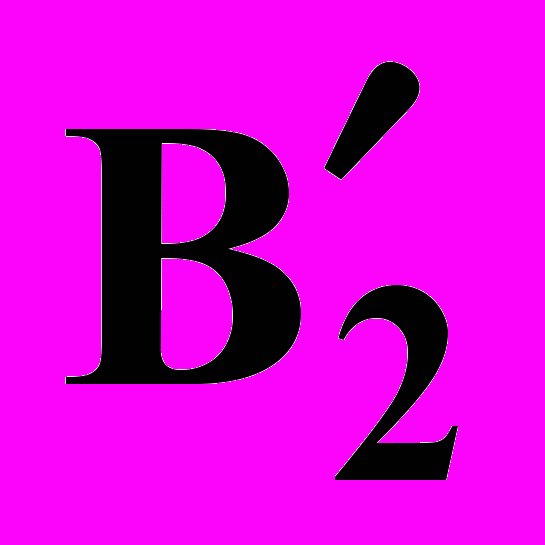 , …,
, …, 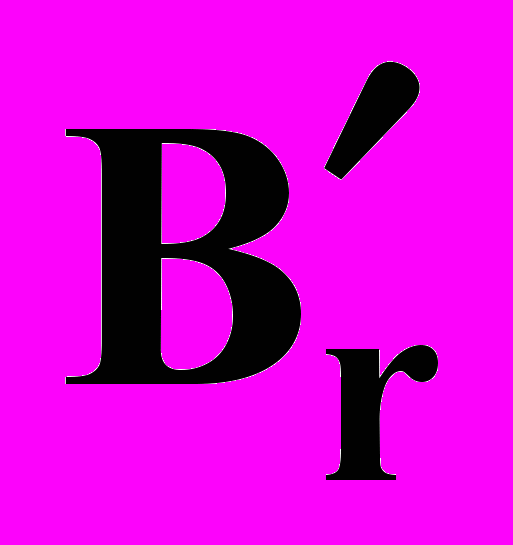 , 0, 0, …, 0) называется базисным вектором.
, 0, 0, …, 0) называется базисным вектором.
Полученное решение (4) системы (1) является допустимым (Х1>0; Х2>0; …Хr>0) и называется базисным (отвечает первому базису).
Подставив в линейную форму критерия оптимальности
R = C1X1 + C2X2 + … + CnXn (2) вместо базисных переменных их выражения через свободные переменные, получим
R =
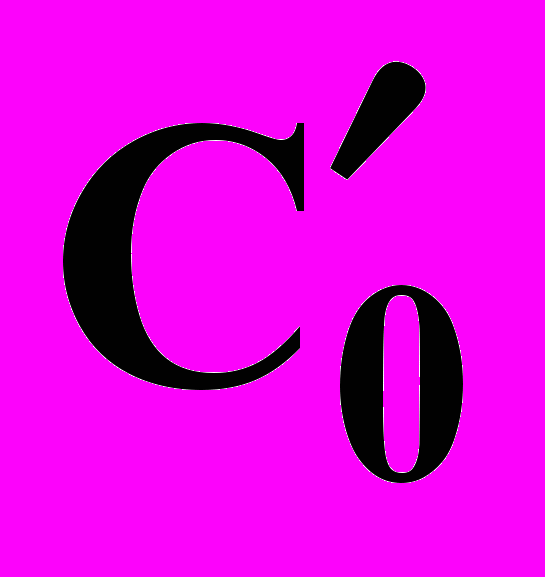 +
+  +
+ 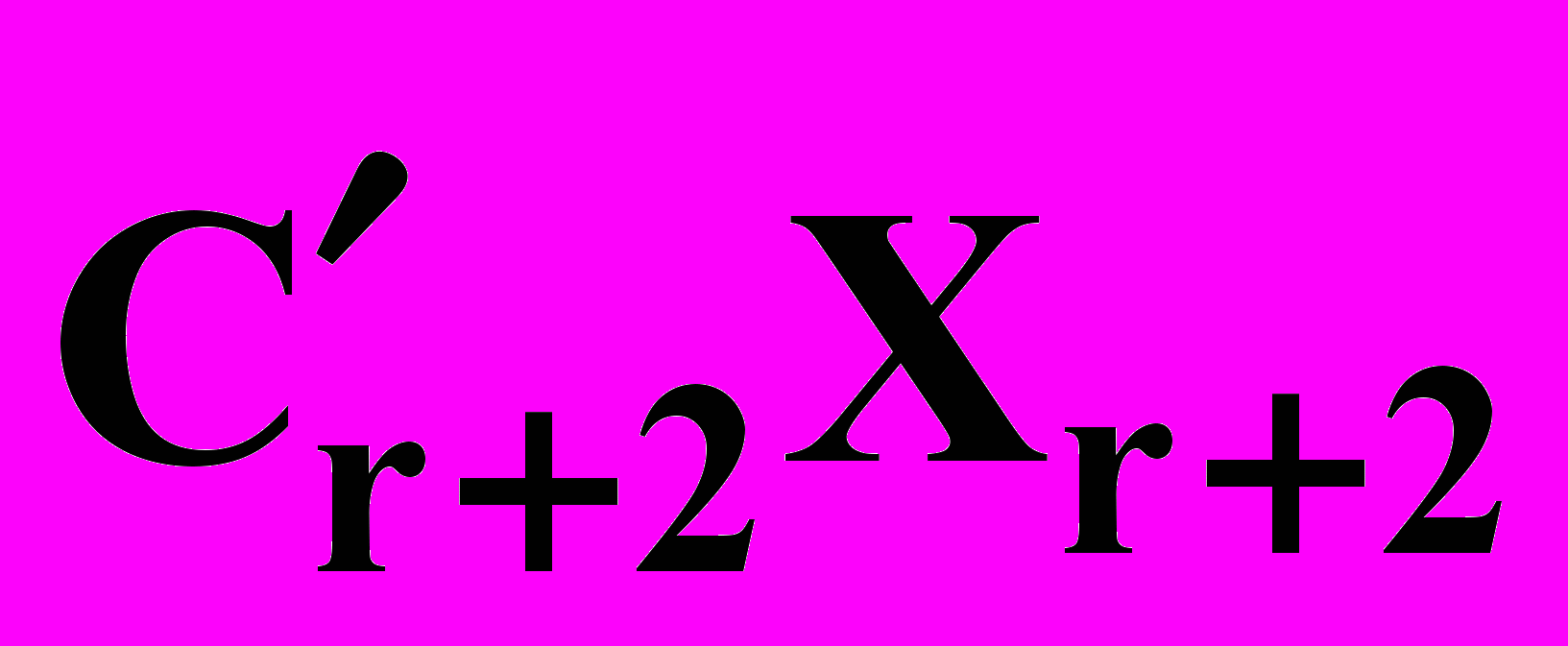 + …+
+ …+ 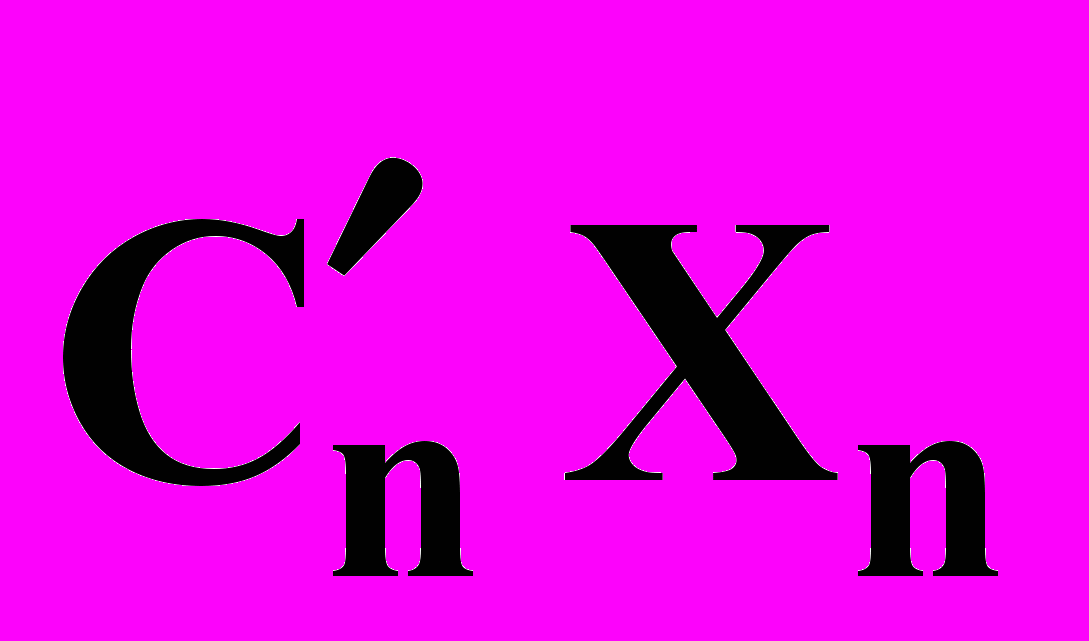 (5)
(5)Причем для первого базисного решения (Xr+i= 0)
R =
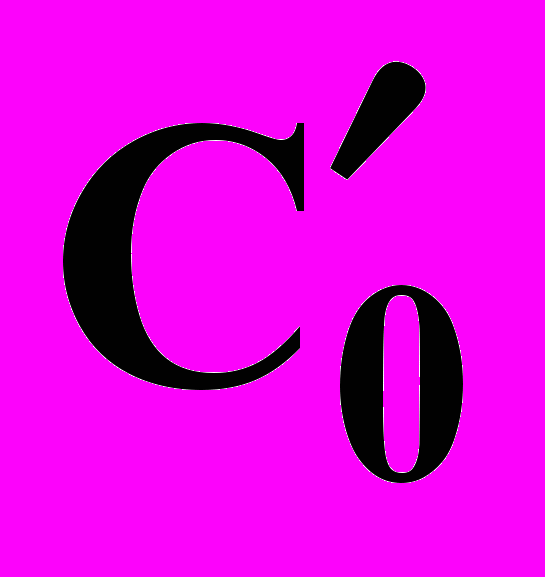 (6)
(6)Далее переходим к другому базисному решению с таким расчетом, чтобы при этом значение линейной формы R не увеличивалось (в случае поиска минимума). Этот переход осуществляется следующим образом – заменяется одна из базисных переменных другой, которая раньше была небазисной (свободной) и т. д. Этот процесс повторяется до тех пор, пока R не достигнет экстремального значения.
2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Работа выполняется в такой последовательности:
- определяется ранг матрицы коэффициентов;
- отыскивается первое базисное решение;
- из анализа целевой функции находится второе базисное решение;
- заменяется одна из базисных переменных на небазисную и определяется новый вид целевой функции;
- отыскивается очередное базисное решение и критерий оптимальности и т.д.
3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Определить оптимальные значения переменных, при которых целевая функция достигает экстремума и соблюдаются следующие ограничения:
| № вар. | Целевая функция | Ограничения |
| 1 | R = X4 – X5 Min | X1 =1 - X4 +2*X5 ; X2 = 2 + 2*X4 - X5 ; X3 = 6 –3* X4 –X5 |
| 2 | R = 6–2*X4 +2*X5 Min | 2*X2 +4*X4 + 6*X5–12=0; 2*X3 –2*X4 – 6*X5–4=0; 2*X1 +2*X4 + 2*X5–4=0 |
| 3 | R = X1 – X2 Min | X3 = 2 + X1 – X2 ; X4 = 5 + X1 – 2*X2 |
| 4 | R =3*X5+2*X4+3 Max | X1 =6 - X4 +2*X5 ; X2 = 4 – 2.X4 - X5 ; X3 = 8 – X4 + 3*X5 |
| 5 | R =X5–X4 +3 Min | 3*X5+X1 +2*X2 =6; X3 –X4 – 3*X5=4; X4 + X5+ X1=4 |
| 6 | R = – X5 + X4 Min | 3–3*X4–X5–X3=0; 1 - X4 +2*X5–X1 =0; 2 + 2*X4 - X5 – X2 = 0 |
| 7 | R = X1 +0.5*X2+ X3 Max | 2*X1 + X2 + X3 + X4 = 3; 3*X1 – X2 + X3 + X5 =4; 2*X1 – 2*X2 – X3 + X6 = 2 |
4, ОФОРМЛЕНИЕ ПРОТОКОЛА
В протоколе по лабораторной работе формулируется цель работы, описываются результаты расчетов по определению экстремуму целевой функции.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Классификация методов решения задач оптимизации.
2. Общая идея методов линейного программирования.
3. Симплекс–метод Данцига, алгоритм расчета.
Литература, рекомендуемая при подготовке к лабoраторным работам
- Царева З.Н., Орлова Е.И. Теоретические основы химической технологии. - Киев: Вища школа, 1986. - 271 с.
2. Закгейм А.Ю. Введение в моделирование химико-технологических процессов- М.Химия 1982-288с.
3. Кафаров В.В. Методы кибернетики в химии и химической технологии - М. Химия, 1985.
- Бояринов А.И.,Кафаров В.В. Методы оптимизации в химической технологии - М. Химия, 1975.-378с.
5. Островский Г.М., Бережинский Т.А. Оптимизация химико-технологических процессов. Теория и практика. - М.: Химия, 1984. - 240 с.
