Методические указания к лабораторным работам по курсу "Математическое моделирование и применение ЭВМ в химической технологии " (часть 2) для студентов 4 курса химико-технологического факультета / Сост.
| Вид материала | Методические указания |
- Методические указания к электронным лабораторным работам по курсу физической химии, 2388.82kb.
- Работам по курсу «Математическое моделирование и проектирование» для студентов магистратуры, 262.63kb.
- И математическое моделирование, 1392.77kb.
- Методические указания к лабораторным работам по физике по практикуму «Вычислительная, 138.12kb.
- Методические указания к лабораторной работе по курсу "Базы данных", 114.06kb.
- Методические указания к лабораторным работам по курсу, 438.32kb.
- Методические указания к лабораторным работам по биологической химии для студентов, 948.06kb.
- Методические указания по лабораторным работам Факультет: электроэнергетический, 554.73kb.
- Методические указания к лабораторным работам для студентов специальности 210100 "Автоматика, 536.56kb.
- Методические указания к лабораторным работам №1-5 для студентов специальности 210100, 363.6kb.
1.3. Определение оптимального температурного режима
для обратимой экзотермической реакции
Под оптимальным температурным режимом процесса понимаются температурные условия, при которых обеспечивается максимальная производительность по целевому продукту в данном реакторе. Такой оптимум может быть обеспечен как при T= const, так и при изменении температуры: во времени для реактора периодического действия; по длине для реактора идеального вытеснения; от аппарата к аппарату для каскада проточных реакторов идеального смешения.
Рассмотрим обратимую экзотермическую реакцию вида А ↔ В, причем энергия активации прямой реакции Е1 меньше энергия активации обратной реакции Е2. В качестве критерия оптимальности для таких реакций обычно используется скорость химического превращения. Тогда целевая функция примет вид:
R = W = Ko1.exp(-E1/(R.T)).CA - Ko2.exp(-E2/(R.T)).CB (15)
В качестве управляющего параметра выбирается температура, поскольку концентрации CA и CB не относятся к входам рассматриваемой системы и зависят от условий протекания реакций. Но при разных значениях концентраций влияние температуры может быть различным. Поэтому данная задача решается в следующей постановке - оптимальная температура определяется при фиксированных значениях CA и CB, т.е. концентрации веществ выступают в качестве ограничений типа равенства. Для обратимой экзотермической реакции при Е2 > Е1 с ростом температуры вначале более существенным будет возрастание скорости прямой реакции, т.к. обратная еще слишком медленна. При дальнейшем повышении температуры обратная реакция, имеющая большую энергию активации, начинает "нагонять" прямую. При данном составе существует температура Травн, при которой смесь находится в равновесии (W = 0), затем ход реакции смещается влево. Где-то посередине имеется температура, при которой скорость реакции максимальна. Это и есть Топт. Продифференцировав (15) по T и приравняв производную нулю, получим:
dW/dT=d[Ko1.exp(-E1/(R.T)). CA-Ko2.exp(-E2/(R.T)). CB]/dT=0 (16)
Преобразовав (16) получим формулу для определения оптимальной температуры:
Топт = (Е2-Е1)/[R.ln(Ko2.E2. CB)/(Ko1.E1. CA)] (17)
Из уравнения (17) следует, что чем выше CA и чем меньше CB, тем выше Топт; по мере роста степени превращения величина Топт уменьшается. При CB → 0 по формуле (8)
Топт → ∞. Поэтому на начальном участке реактора следует устанавливать максимально допустимую температуру Тмакс, а с момента, когда определенная по уравнению (1.17) Топт сравнивается с Тмакс, изменение температуры должно определяться этим уравнением. Для того, чтобы определить оптимальный профиль температур в реакторе и найти отсюда максимальную скорость образования целевого продукта, нужно знать состав исходной смеси на входе в аппарат и зависимость скорости реакции от температуры. На основании этих данных можно вычислить скорость реакции как функцию температуры при различных фиксированных значениях степени превращения. Представив полученные результаты графически в координатах W = f(T),
для каждого значения степени превращения определяется температура, при которой скорость реакции максимальна. На основании полученных данных строится график X = f(T), который и представляет собой оптимальный температурный режим. Для расчета скорости реакции можно пользоваться следующей формулой:
W = K1.Cao.(1 - X - X/Kc) (18)
где K1 = Ko1.exp(-E1/(R.T)) - константа скорости прямой реакции;
Kc = exp(E2/T - F) - константа равновесия; F - коэффициент;
Сао - начальная концентрация компонента А, моль/куб.м;
Х - степень превращения.
Расчеты проводятся для 6 - 8 значений степени превращения в диапазоне Х = 0.1 - 0.9. Число точек по температуре должно быть не менее 8 - 10. Начальная концентрация компонента Сао = 1.
2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Определить оптимальное время пребывания и максимальную концентрацию целевого продукта В для двух последовательных реакций первого порядка А B D в реакторе идеального вытеснения, используя формулы ( 10 ) и ( 12 ). Из уравнений материального баланса (14) получить выражения для определения оптимального времени пребывания и максимальной концентрации целевого продукта В и вычислить их значения для тех же реакций в реакторе идеального смешения; Сравнить показатели, достигаемые в РИС и РИВ. Для обратимой экзотермической реакции А ↔ В при заданных значениях параметров рассчитать зависимость скорости реакции как функцию температуры при различных фиксированных значениях степени превращения. Из графика в координатах W = f(T) определить условия, при которой скорость реакции максимальна. На основании полученных данных построить оптимальный температурный режим в координатах X = f(T).
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Исходные данные, необходимые для расчетов, приведены в табл.1 (для пп 1.1 и 1.2) и в табл.2 (для пп 1.3.). Номер варианта соответствует порядковому номеру фамилии студента по журналу.
Таблица 1. Варианты индивидуальных заданий
| № | Группа 1 | Группа 2 | № | Группа 1 | Группа 2 | ||||
| 1 | 0.1 | 0.05 | 0.3 | 0.16 | 13 | 0.3 | 0.13 | 0.20 | 0.06 |
| 2 | 0.5 | 0.07 | 0.5 | 0.07 | 14 | 0.5 | 0.09 | 0.5 | 0.16 |
| 3 | 0.2 | 0.08 | 0.25 | 0.09 | 15 | 0.2 | 0.14 | 0.35 | 0.11 |
| 4 | 0.15 | 0.06 | 0.4 | 0.07 | 16 | 0.35 | 0.18 | 0.15 | 0.05 |
| 5 | 0.3 | 0.09 | 0.15 | 0.09 | 17 | 0.1 | 0.2 | 0.1 | 0.09 |
| 6 | 0.4 | 0.16 | 0.2 | 0.11 | 18 | 0.15 | 0.19 | 0.25 | 0.17 |
| 7 | 0.5 | 0.11 | 0.5 | 0.19 | 19 | 0.3 | 0.2 | 0.4 | 0.18 |
| 8 | 0.25 | 0.07 | 0.35 | 0.14 | 20 | 0.5 | 0.05 | 0.5 | 0.13 |
| 9 | 0.1 | 0.13 | 0.15 | 0.08 | 21 | 0.16 | 0.12 | 0.32 | 0.08 |
| 10 | 0.35 | 0.09 | 0.4 | 0.13 | 22 | 0.25 | 0.14 | 0.12 | 0.07 |
| 11 | 0.15 | 0.12 | 0.3 | 0.06 | 23 | 0.32 | 0.13 | 0.18 | 0.05 |
| 12 | 0.25 | 0.15 | 0.1 | 0.07 | 24 | 0.5 | 0.11 | 0.48 | 0.14 |
Таблица 2. Варианты индивидуальных заданий
-
№
Ko1.(E-7)
E1.(E-4)
E2.(E-3)
F.(E-1)
Температура,С
1
0.0078
3.30
9.50
1.91
150 - 280
2
2.9
3.80
8.00
2.20
25 - 95
3
0.06
3.38
8.40
1.87
100 - 220
4
0.015
2.64
9.35
1.91
160 - 260
5
3.2
4.66
9.09
2.233
35 - 175
6
0.007
3.42
10.15
1.66
250 - 350
7
0.0009
3.00
8.90
1.80
100 - 250
8
2.7
4.56
9.50
2.046
70 - 175
9
0.2
4.10
10.00
2.01
150 - 220
10
3.0
4.856
9.06
2.746
25 - 95
11
0.0064
2.83
9.60
1.78
150 - 300
12
0.9
3.64
7.65
1.92
70 - 140
13
3.5
4.36
9.40
2.246
70 - 175
14
0.003
3.05
10.95
1.72
250 - 400
15
2.9
3.80
6.70
1.90
25 - 95
16
0.05
2.80
8.60
1.90
95 - 205
17
0.21
3.75
10.40
2.45
90 - 180
18
0.017
2.94
8.35
1.81
100 - 200
19
0.24
3.38
10.10
1.93
130 - 230
20
0.035
3.62
9.10
1.91
60 - 130
21
0.0064
2.83
9.60
1.78
160 - 280
22
0.9
3.64
7.65
1.92
80 - 170
23
3.5
4.36
9.40
2.246
60 - 180
24
0.003
3.05
10.95
1.72
230 - 380
ОФОРМЛЕНИЕ ПРОТОКОЛА
В протоколе по лабораторной работе формулируется цель работы, приводятся результаты расчетов по определению оптимального времени пребывания и максимальной концентрации целевого продукта В для двух последовательных реакций первого порядка А → B → D в реакторах идеального вытеснения и идеального смешения и их сравнение, описываются расчеты по определению максимальных значений скорости химического превращения, приводятся графики зависимостей W = f(T) и X = f(T).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Классификация методов решения задач оптимизации.
2. Критерий оптимальности. Целевая функция. Требования, предъявляемые к критерию оптимальности.
3. Виды критериев оптимальности.
4. Условия существования экстремума функции.
5. Основные особенности моделей РИВ и РИС.
6. Определение оптимального времени пребывания в РИВ.
7. Определение оптимального времени пребывания в РИС.
8. Оптимальный температурный режим для обратимой экзотермической реакции.
9. Условия выбора управляющих параметров.
ЛАБОРАТОРНАЯ РАБОТА 12
МЕТОДЫ ОДНОМЕРНОГО ПОИСКА ДЛЯ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ
ЦЕЛЬ РАБОТЫ: – составить блок-схему и программу для определения экстремума функции методом сканирования;
– составить подпрограмму для расчета целевой функции;
– определить точки экстремума целевой функции с использованием составленной программы по методу сканирования и прикладных программ по методам локализации экстремума и "золотого сечения";
– сопоставить эффективность используемых методов.
1. ОПИСАНИЕ МЕТОДИКИ РАСЧЕТОВ
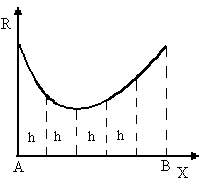
Для всех методов постановка задачи следующая – определить положение экстремума (минимума) на интервале [А,В].
1.1. Метод cканирования
Алгоритм метода следующий. Интервал поиска [A,B] разбивается на N равных участков, каждый из которых равен шагу поиска h. Далее последовательно определяется значение целевой функции во всех точках разбиения, включая точки А и В, и запоминается минимальное (максимальное) значение целевой функции (рис.1). Таким образом, экстремальное значение функции может быть найдено с точностью до величины шага поиска.
рРис.1
1.2. Метод локализации экстремума
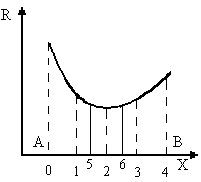
Интервал поиска [A,В] разбивается на 4 равные части и в точках разбиения и на границах интервала вычисляется значение целевой функции - в точках 0,1,2,3 и 4(рис.2). Локализуется положение экстремума (минимума) на интервале в два раза меньшем [2;4], чем предыдущий [0;4]. Полученный интервал снова делим на 4 равные части.
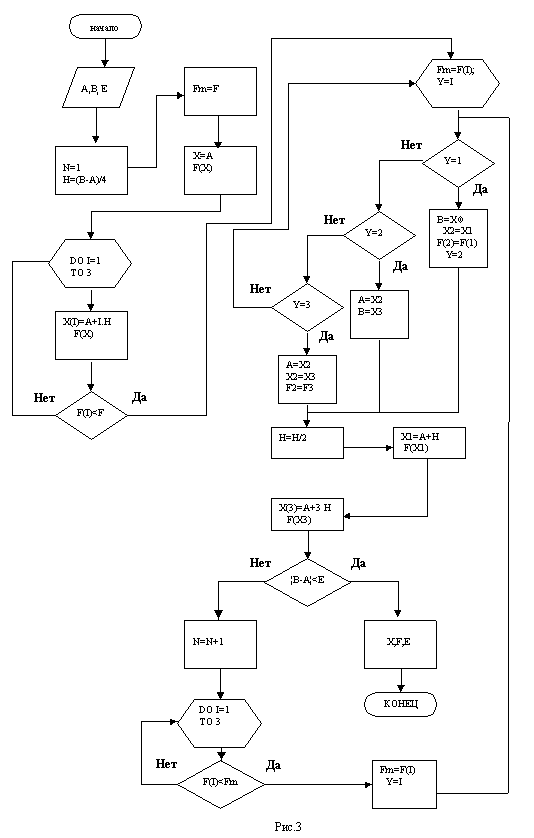
Локализация экстремума продолжается до тех пор, пока не будет достигнута заданная точность. Блок-схема программы "LOCEXT1", реализующую данный метод, приведена на рис.3
Рис.2
1.3. Метод "золотого сечения"
В основе этого метода лежит закон геометрического отношения или "золотого сечения". Пусть дан отрезок а, который разделен на две неравные части b и c так, что выполняется отношение:
a / b = b / c или a.c = b 2 (1)
В соответствии с этим законом определяются точки исследуемого интервала, в которых необходимо производить вычисление целевой функции. Поскольку с = а – b, то подставив выражение для с в (1) и введя новую переменную k = b / a, после преобразований получим:
k2 + k - 1 = 0 (2)
БЛОК-СХЕМА МЕТОДА ЛОКАЛИЗАЦИИ ЭКСТРЕМУМА
Решив (2), получим приближенное значение k=0.62.
П
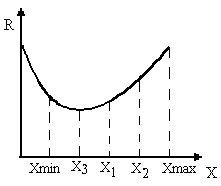
орядок поиска экстремума методом "золотого сечения" следующий. На исследуемом интервале определяются две точки X1 и X2:
X1 = Xmin + (1-k).a
