Методические указания к лабораторным работам по курсу "Математическое моделирование и применение ЭВМ в химической технологии " (часть 2) для студентов 4 курса химико-технологического факультета / Сост.

Вид материала

2. Порядок выполнения работы
3. Индивидуальные задания
Оформление протокола
Контрольные вопросы
Блок-схема метода "золотого сечения"
Лабораторная работа n 13
1. Симплексный метод
1.2. Алгоритм симплексного метода
2. Метод нелдера-мида
2. Порядок выполнения работы
2.1 Составление подпрограммы для расчета целевой функции
2.2. Работа с головными программами "SIMPL_M.BAS" и "NED_MID.BAS"
Gamma = 2.
Оформление протокола
Контрольные вопросы
Лабораторная работа n 14
1. Описание методики расчетов
1.1. Метод покоординатного спуска
1.2. Метод Хука-Дживса.
2.Порядок выполнения работы
...
Полное содержание

Подобный материал:

1 2 3 4 5 6

X2 = Xmin + k.a

где а - длина интервала Xmax - Xmin.

В точках X1 и X2 рассчитывается целевая функция. По найденным значениям R(X1) и R(X2) с учетом R(Xmin) и R(Xmax) определяется подинтервал, в

котором локализован экстремум. В данном случае это –

[Xmin,X2]. Далее внутри подинтервала [Хmin,X2] находится точка Х3:

Х3 = Xmin + (1-k).a

где а - длина подинтервала [Xmin,X2]. Рис.4

Далее вычисляется значение целевой функции R(X3)и сравниваются значения R(X2),R(X1),R(X3). Находится минимальное значение (в данном случае R(X3) и процедура продолжается - определяется аналогично точка Х4 и т.д., пока не будет найден экстремум с заданной точностью. Блок-схема программы "LOCEXT2", реализующую данный метод, приведена на рис.5.

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Работа выполняется в такой последовательности:

составляют программу для определения экстремума (минимума) методом сканирования;

- выполняют расчеты на ЭВМ по составленной программе (метод сканирования) и прикладным программам "LOCEXT1" (метод локализации экстремумов) и "LOCEXT2" (метод "золотого сечения");

- дается оценка сравнения эффективности методов.

3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

В таблице 1 приведены целевые функции и область допустимых изменений исследуемых независимых переменных. Требуемая точность определения координат точки экстремума 0.001.

ОФОРМЛЕНИЕ ПРОТОКОЛА

В протоколе по лабораторной работе описываются результаты расчетов, выполненных на ЭВМ. Приводится блок-схема программы по методу сканирования, листинг программы и распечатки расчетов.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие существуют методы одномерного поиска?

2. Суть методов одномерного поиска.

3. Метод сканирования. Алгоритм расчета.

4. Блок-схема метода сканирования.

5. Метод локализации экстремума. Алгоритм расчета.

6. Блок-схема метода локализации экстремума.

7. Метод "золотого сечения". Алгоритм расчета.

8. Блок-схема метода "золотого сечения".

9. Сравнительная характеристика методов одномерного поиска.

БЛОК-СХЕМА МЕТОДА "ЗОЛОТОГО СЕЧЕНИЯ"

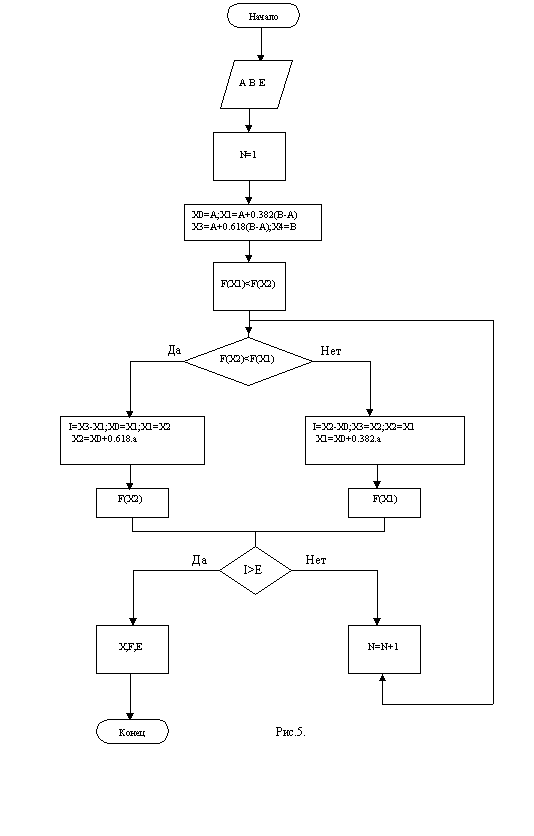
Таблица 1.

Исходные данные для индивидуальных заданий

№ ва- рианта	Целевая функция R(x)	Диапазон изменения Переменных
1	4.4х³ – 9.2х² – 7.3х +10.97	0; 10
2	0.4х³ + 2.5х ²–14х +2	0; 10
3	0.2х⁴ – 1.5х³ – 4х + 25	0, 10
4	0.5х⁴ – 8х² + 2х +2	0; 10
5	0.2х⁴ – 0.7х³ – 6.5х + 8.2	0; 10
6	4х⁴ – 9х³ +2х² – 8х +2	0, 10
7	3х³ – х² – 13х – 660	0; 10
8	Х³ – 0.39х² –10.5х +11	0; 10
9	Х³ – 1.473х² –5.738х + 6.763	0, 10
10	0.8х⁴ + 0.35х² –.8х + 0.8	0; 10
11	х³ – 16х² +25х + 44	0; 10
12	х³ – 10х –760	0, 10
13	1.6х⁴ – 2.7х² +11.3х –160.6	-10, 0
14	3х⁴ – 7х² +13х – 65.3	-10, 0
15	х⁴ -2х² + 9х – 16.8	-10, 0
16	2х⁴ – 5х² +10х – 34.81	-10, 0
17	х⁴ – 5х² +14х – 1200	-10, 0
18	0.1х³ +х² – 4х –20	-10, 5
19	х⁴ – 2х² +5х –3.2	-10, 0
20	4.2х³ -9.1х² -7.2х+12	- 3, 9

ЛАБОРАТОРНАЯ РАБОТА N 13

СИМПЛЕКСНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ

ЦЕЛЬ РАБОТЫ: – составить подпрограмму для расчета целевой функции;

– определить точки экстремума целевой функции с использованием прикладных программ, реализующих симплексный метод и метод Недлера-Мида;

– сопоставить эффективность используемых методов.

1. СИМПЛЕКСНЫЙ МЕТОД

1.1. Описание методики расчетов

Основная идея этого метода заключается в том, что по известным значениям целевой функции в вершинах выпуклого многогранника называемого симплексом, находится направление, в котором требуется сделать следующий шаг, чтобы получить наибольшее уменьшение (увеличение) значения целевой функции. При этом под симплексом в n-мерном пространстве понимается многогранник, имеющий n+1 вершину. Примером симплекса в двухмерном пространстве, т.е. на плоскости, является треугольник. В трехмерном пространстве - тетраэдер.

Симплекс обладает следующим свойством - против любой из его вершин

расположена только одна грань, на которой можно построить новый симплекс, отличающийся от прежнего расположением новой вершины

, тогда как остальные вершины обоих симплексов совпадают. Вершина нового симплекса

, вообще говоря, может находиться и по другую сторону грани от вершины

. Это свойство симплекса и обусловило возможность его применения при решении задач оптимизации.

1.2. Алгоритм симплексного метода

Пусть вершинам исходного симплекса S_i (i=1,2,...,n+1) отвечают координаты

U=(U1,U2,...,U_n), (i=1,2,...,n+1). Наибольшее значение целевой функции соответствует вершине S_js . Определим координаты вершины S_j нового симплекса. Вершина S_j располагается симметрично вершине S_js относительно середины грани, находящейся против вершины S_js. Координаты центра этой грани U определяются по формуле:

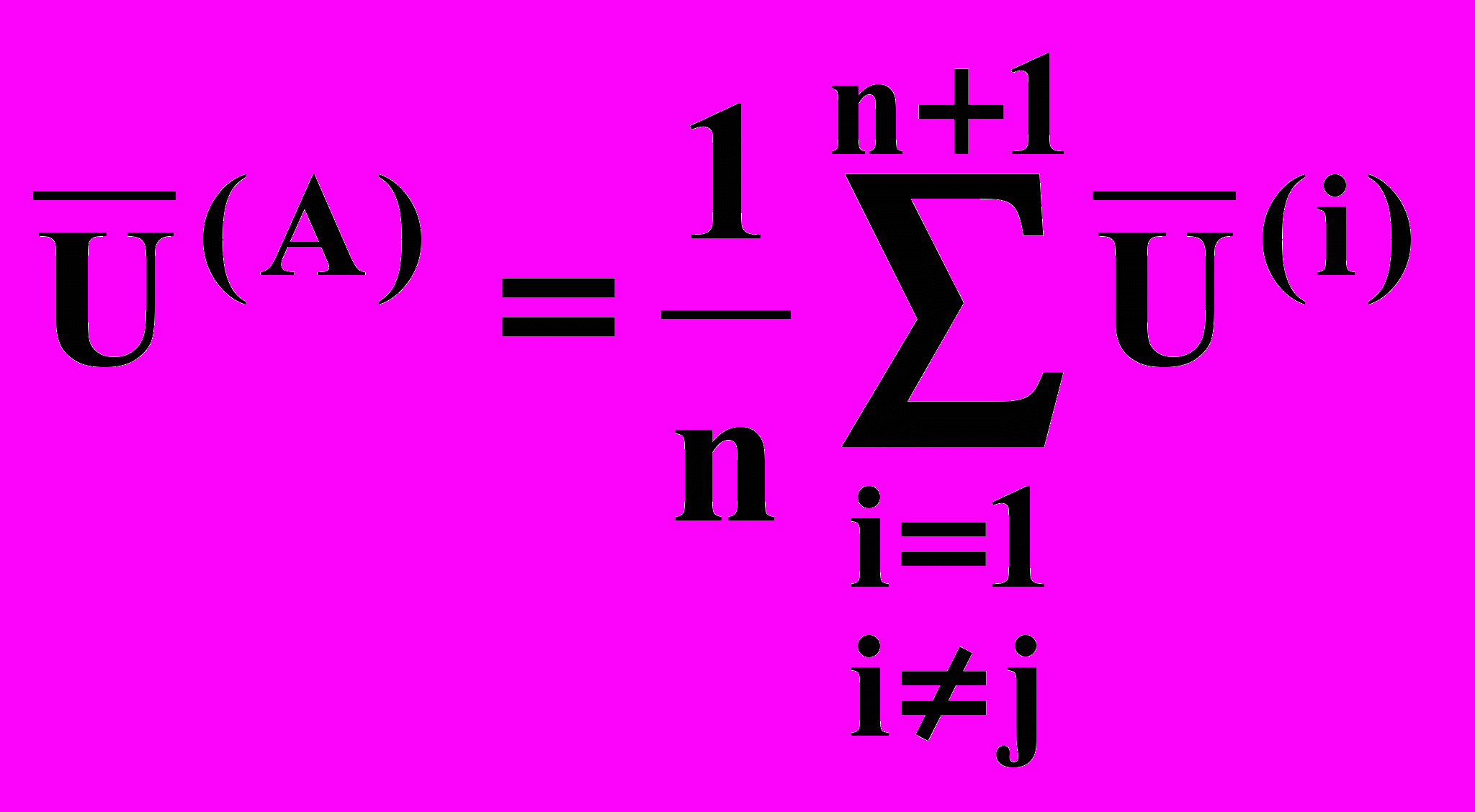(13.1)

причем суммирование ведется только по тем векторам U , которые отвечают вершинам

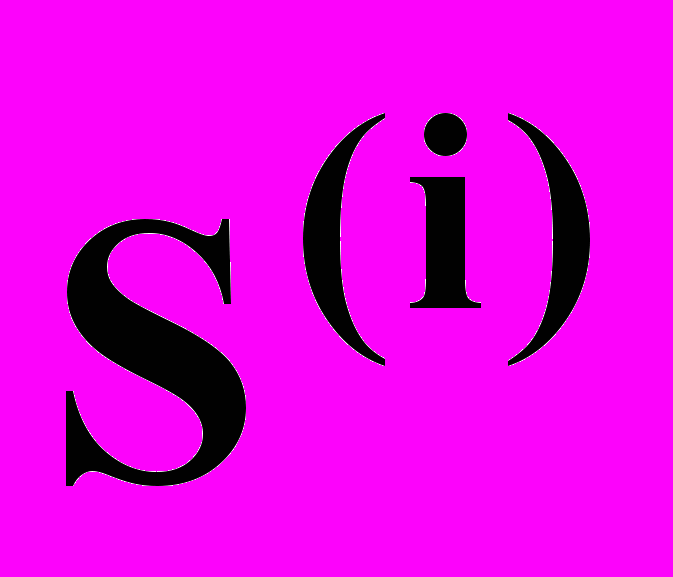, образующим эту грань. Вектор L, характеризующий расстояние от вершины S_js до центра противолежащей грани, будет равен:

L =

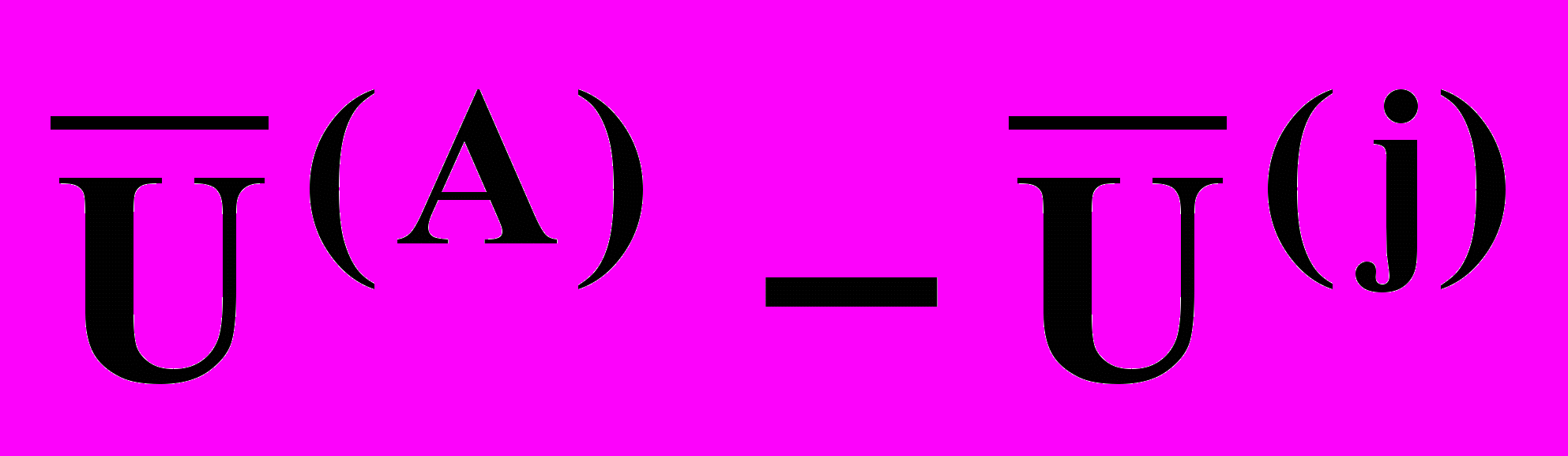(13.2)

Координаты вершины

определяется по формуле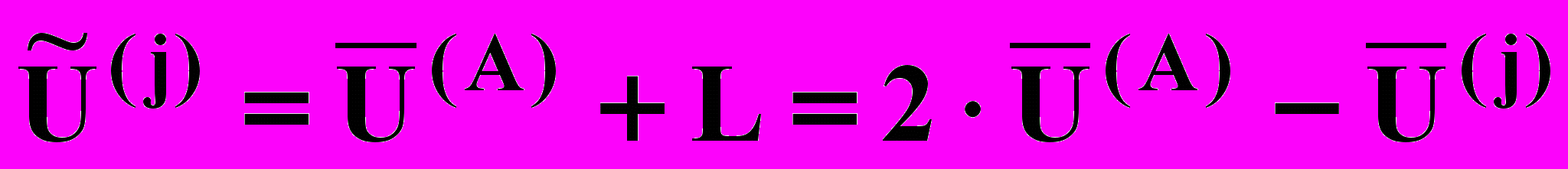

(13.3)

Подставив в выражение для

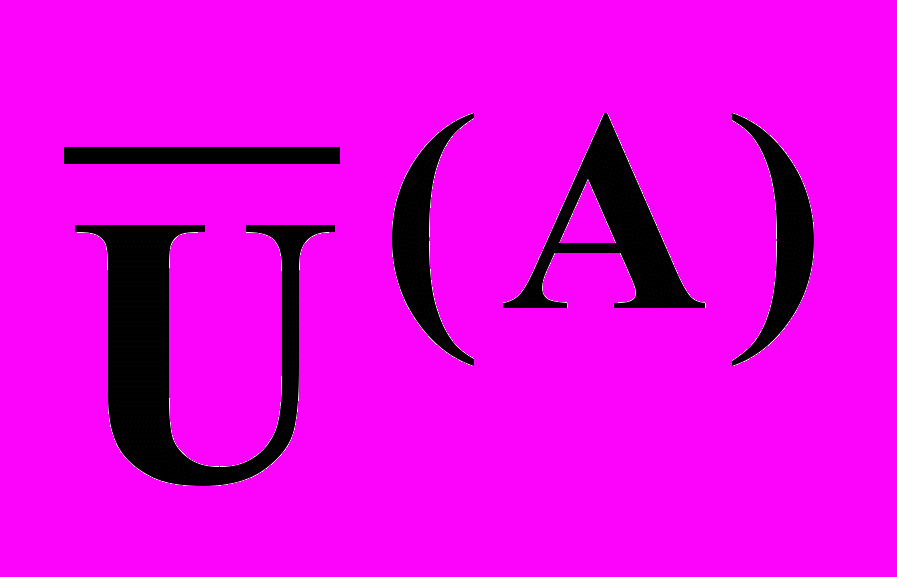из (13.1), получим: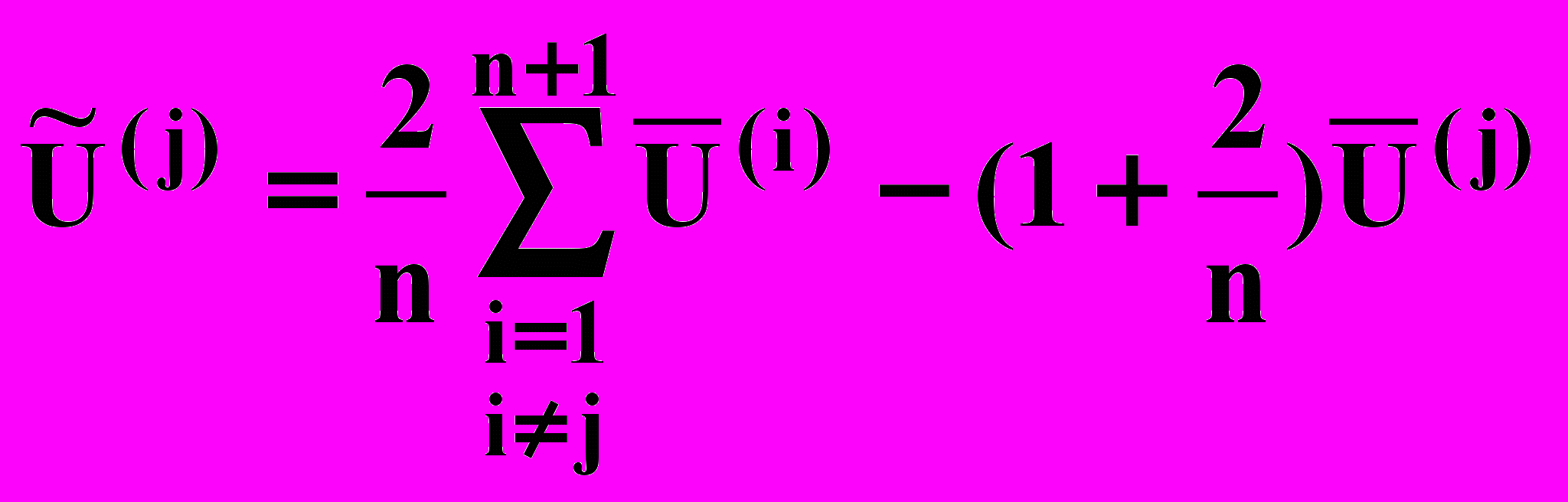

(13.4)

Формула (13.4) определяет координаты вершины

нового симплекса. При необходимости уменьшить размеры симплекса (в случае зацикливания в окрестности точки оптимума) вместо формулы (13.2) можно пользоваться следующим выражением:

L = 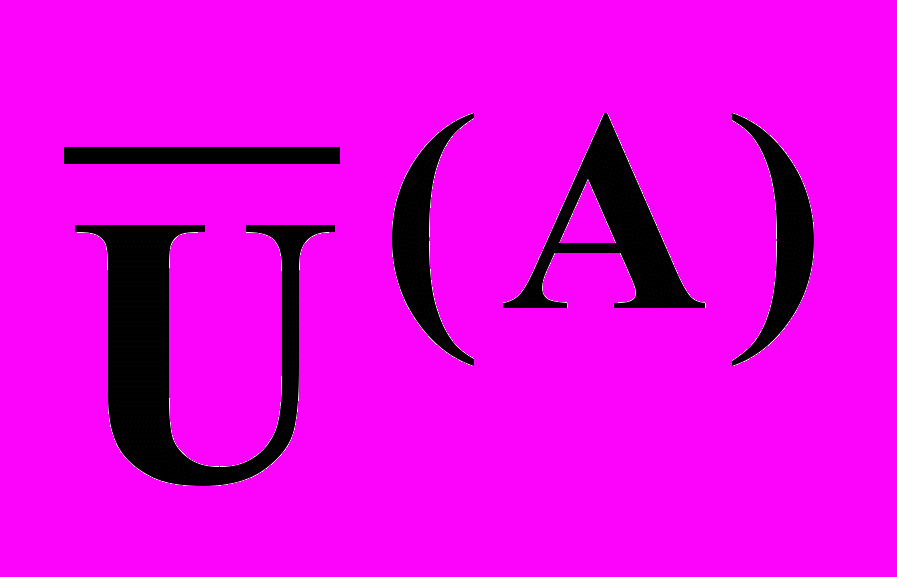+ 1/2ыL = 3/2 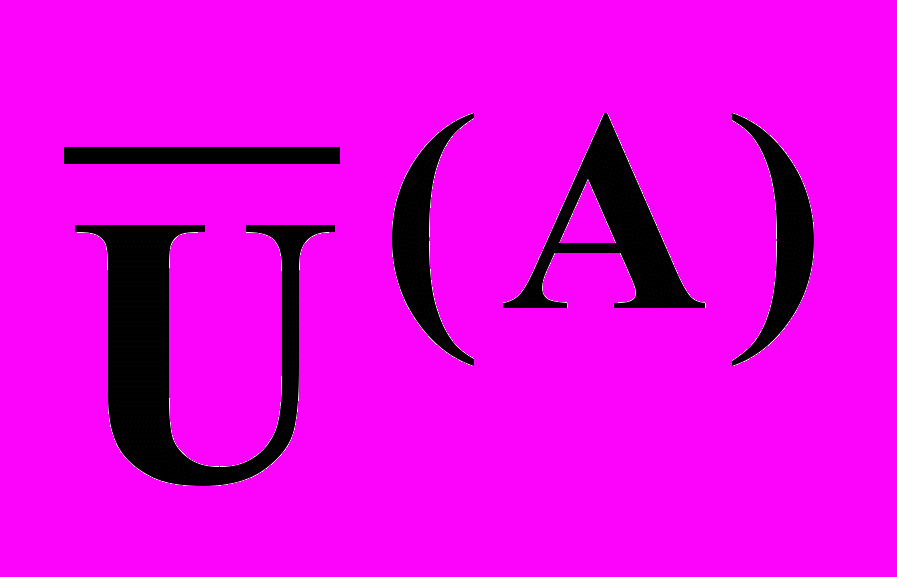-1/2 (13.5)

Наиболее эффективно симплексный метод сходится при использовании правильных симплексов - равносторонннего треугольника или тертаэдра, образованного равносторонними треугольниками. В этом случае направление поиска совпадает с направлением градиента (если симплекс достаточно мал). Симплексный метод обладает еще одним важным достоинством - при увеличении размерности задачи вычислительные затраты возрастают незначительно, т.к. на каждом шаге считается только одно значение целевой функции. Блок-схема приведена на рис.6

2. МЕТОД НЕЛДЕРА-МИДА

2.1. Описание методики расчетов

Метод Недлера-Мида является развитием симплексного метода Спендли, Хекста и Химсворта. Множество n+1-й равноудаленной точки в n-мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. Идея метода состоит в сравнении значений функции в n+1 вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры. В данном методе симплекс перемещается с помощью трех операций: отражения, растяжения и сжатия. Смысл этих операций станет понятным при рассмотрении шагов процедуры.

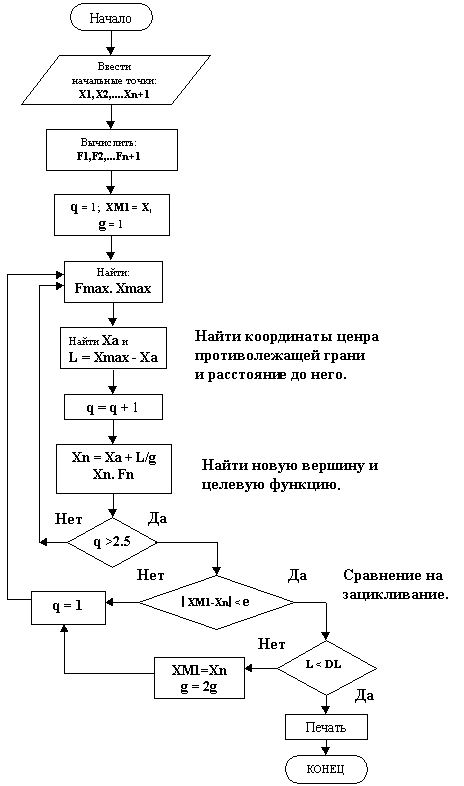
Рис.6. Блок-схема симплексного метода

А. Найдем значения функции в вершинах симплекса.

f₁= f(x₁); f₂=f(x₂);.....f_n+1=f(x_n+1)

Б. Найдем наибольшее значение функции f_h, следующее за наибольшим значением функции f_g, наименьшее значение функции f_l и соответствующие им точки X_h, X_g, и X_l.

В. Найдем центр тяжести всех точек, за исключением точки X_h.

X_о=

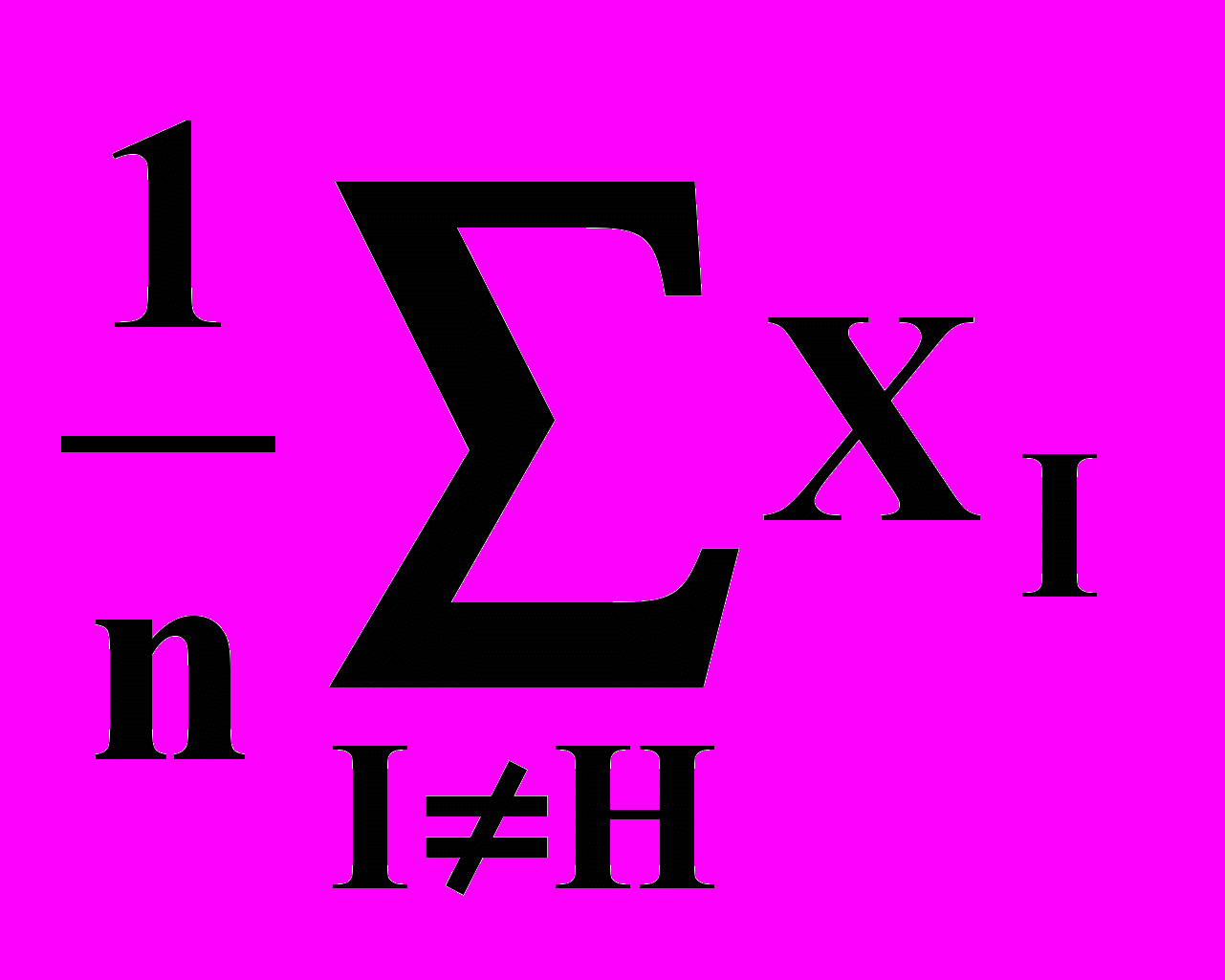(13.6)

Вычислим f(X_о)=f_о .

Г. Удобнее всего начать перемещение от точки Х_h. Отразив точку Х_h относительно точки Х_о, получим точку Х_r и найдем f(Х_r) = f.

Если α > 0 - коэффициент отражения, то положение точки X_r определяется следующим образом:

X_r= (1 + α ) Х_о – α. Х_h (13.7)

где α = │ Х_r – Х_о │ ⁄ │ Х_о – Х_h │

Д.Сравним значения функций f_r и f_l.

1.Если f_r < f_l, то получим наименьшее значение функции. Направление из точки Х_о в точку Х_r наиболее удобно для перемещения. Таким образом, мы производим растяжение в этом направлении и находим точку Х_e и значение функции f_e = f(X_e). Коэффициент растяжения γ > 1 можно найти из следующих соотношений:

X_e - X_o = γ.(X_r - X_o),

т.е.

X_e = γ .X_r + (1 - γ ) X_o.

Где γ = │ X_e - X_o │ / │ X_r - X_o │ .

а) Если f_e < f_l, то заменяем точку X_h на точку X_E и проверяем (n + 1)- ую точку симплекса на сходимость к минимуму (см. шаг 3).

Если сходимость достигнута, то процесс останавливается; в противном случае возвращаемся на шаг Б.

б) Если f_e ≥ f_l, то отбрасываем точку f_e. Очевидно, мы переместились слишком далеко от точки X_o к точке X_r. Поэтому следует заменить точку X_h на точку X_r, в которой было получено улучшение (шаг Д, 1), проверить сходимость и, если она не достигнута, вернуться на шаг В.

2. Если f_r > f_l, но f_r ≤ f_g, то X_r является лучшей точкой по сравнению с другими двумя точками симплекса и мы заменяем точку X_h на точку X_r и, если сходимость не достигнута, возвращаемся на шаг Б, т.е. выполняем пункт 1, б, описанный выше.

3. Если f_r > f_l, но f_r > f_g, то перейдем на шаг Е.

Е. Сравним значения функций f_r и f_H.

1. Если f_r > f_H, то переходим непосредственно к шагу сжатия Е,2. Если f_r < f_H, то заменяем точку X_h на точку X_r и значение функции f_H на значение функции f_r. Запоминаем значение f_r > f_g из шага Д.2, приведенного выше. Затем переходим на шаг Е, 2.

2. В этом случае f_r > f_H, поэтому ясно, что мы переместились слишком далеко от точки X_h к точке X_o. Попытаемся исправить это, найдя точку X_c (а затем f_c) c помощью шага сжатия.

Если f_r > f_H, то сразу переходим к шагу сжатия и находим точку X_cиз соотношения

X_c - X_o = β . (X_h - X_o),

где (0 < β < 1) - коэффициент сжатия.

Тогда X_c = β .X_h + (1 - β ) X_o.

Если f_r < f_H, то сначала заменим точку X_h на точку X_r, затем произведем сжатие. Тогда точку X_c найдем из соотношения X_c - X_o = β .(X_r - X_o), т.е. X_c = β .X_r + (1 - β ) X_o

Ж. Сравним значения функций f_c и f_H.

1.Если f_c < f_H, то заменяем точку X_h на X_c,и если сходимость не достигнута, то возврашаемся на шаг Б.

2.Если f_c > f_H, то очевидно, что все наши попытки найти значение меньшее f_H закончились неудачей, поэтому мы переходим на шаг З.

З. На этом шаге мы уменьшаем размерность симплекса делением пополам расстояния от каждой точки симплекса до X_l– точки определяющей наименьшее значение функции. Таким образом, точка X_i заменяется на точку X_i +1/2(X_i - X_l), т.е. заменяем точку X_i точкой 1/2 (X_i + X_l). Затем вычисляем f_i для i = 1,2,..., (n + 1), проверяем сходимость и, если она не достигнута, возвращаемся на шаг В.

И. Проверка сходимости основана на том, чтобы стандартное отклонение (n + 1) -го значения функции было меньше некоторого заданного малого значения. В этом случае вычисляется

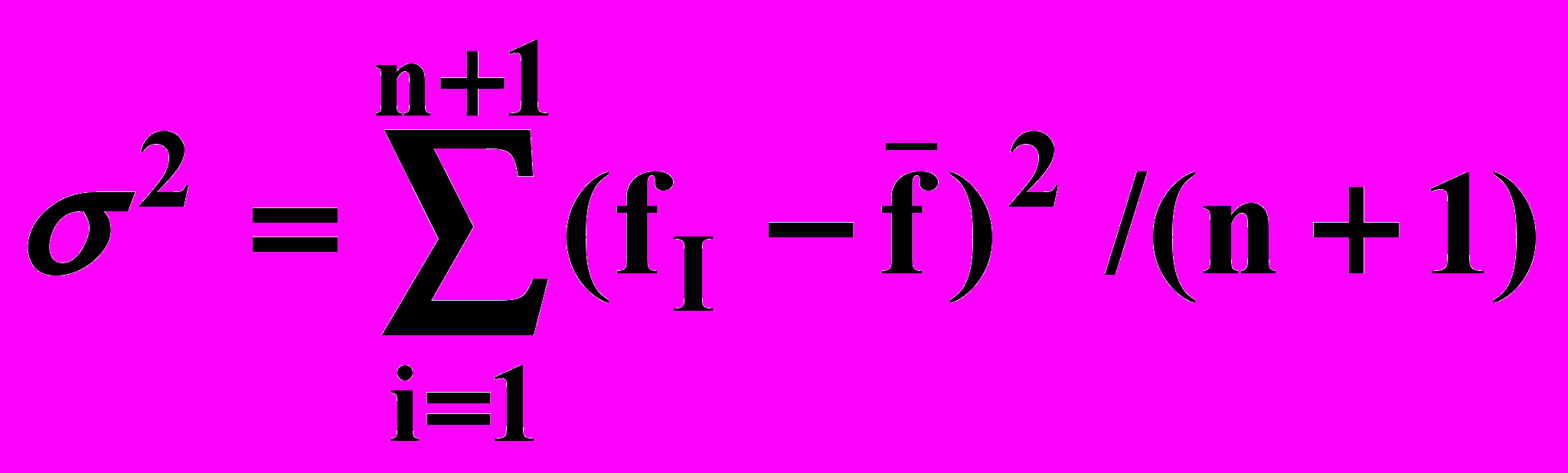
где

.

Если

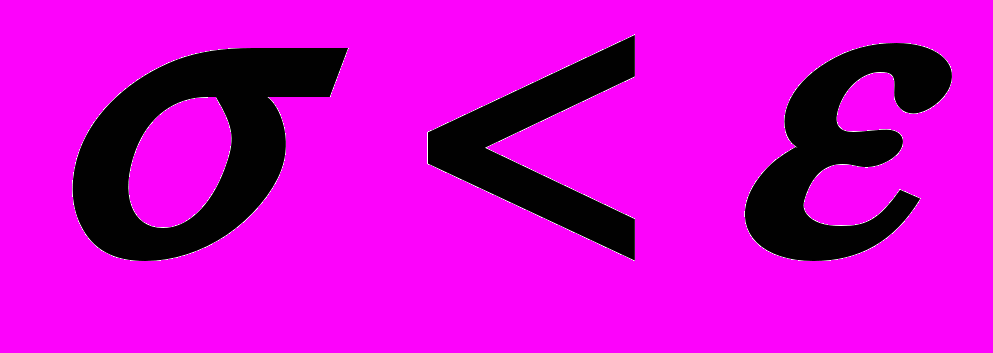, то все значения функции очень близки друг к другу и поэтому они, возможно, лежат вблизи точки минимума функции X_l. Шаги этой процедуры представлены в виде блок-схемы на рис.7.

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Работа выполняется в такой последовательности:

- составляют и транслируют процедуру-подпрограмму для расчета выбранной целевой функции;

- выполняют расчеты на ЭВМ по программе "SIMPL_M.BAS" (реализующей симплексный метод) и , по программе "NED_MID.BAS" (реализующей метод Нелдера-Мида), находящихся на диске Z в директории МЕT_MMO\LAB.3, в результате которых определяют значение минимума целевой функции.

- по известному алгоритму составляется блок-схема программы расчета минимума целевой функции по симплексному методу;

- дается оценка сравнения эффективности методов.

2.1 Составление подпрограммы для расчета целевой функции

Расчет целевой функции выполняется процедурой-подпрограммой, которую нужно составить на языке QuickBASIC. В качестве примера приводится текст процедуры расчета следующей целевой функции:

Z = 100 * (X₂–X₁²)²+ (1 – X₁)²

Для программы "SIMPL_M.BAS":

REM Function

Fun1:

Z = 100 * (x(2) - x(1) 2) 2 + (1 - x(1)) 2

RETURN

Для программы "NED_MID.BAS":

2340 END

5000 Z = 100 * (X(2) - X(1) 2) 2 + (1 - X(1)) 2

5060 TEV = TEV + 1

5100 RETURN

Р

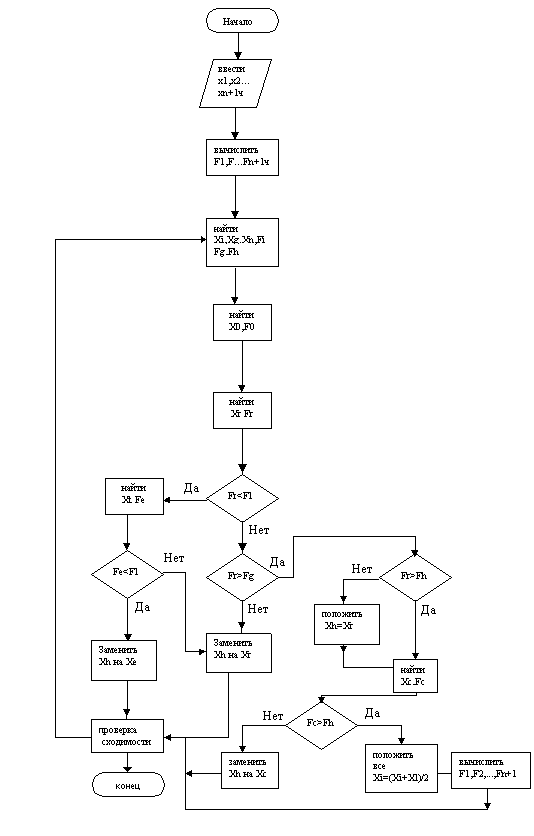
ис.7. Блок-схема метода Нелдера-Мида

2.2. Работа с головными программами "SIMPL_M.BAS" и "NED_MID.BAS"

Ввод исходных данных в этих программах организован в диалоговом режиме. Поэтому для запуска необходимо на диске U в директории LANG\QBX\BIN найти и запустить головной файл qbx.exe, после чего загрузить программу "SIMPL_M.BAS" или "NED_MID.BAS". Находясь в режиме редактирования составить и записать подпрограмму для расчета целевой функции. Комбинацией клавиш Shift+F5 запустить программу в работу. В качестве исходных данных для программы "SIMPL_M.BAS" вводятся число переменных, точность вычислений, координаты n+1 вершины симплекса. Для программы "NED_MID.BAS" задаются начальное приближение, длина шага, вводятся значения ALFA, BETA, GAMMA. Рекомендуется брать ALFA = 1, BETA = 0.5, GAMMA = 2.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

В таблице 1 приведены целевые функции. Номер варианта соответствует порядковому номеру фамилии студента по журналу.

ОФОРМЛЕНИЕ ПРОТОКОЛА

В протоколе по лабораторной работе формулируется цель работы, описываются результаты расчетов, выполненных на ЭВМ. Также в протокол включаются листинг подпрограмм и распечатки расчетов,

блок-схема программы, реализующей симплексный метод.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Классификация методов решения задач оптимизации.

2. Общая идея методов нелинейного программирования.

3. Симплексный метод, алгоритм расчета.

4. Блок-схема симплексного метода.

5. Метод Нелдера-Мида, алгоритм расчета.

6. Физический смысл операции отражения, растяжения и сжатия.

7. Сравнение метода Нелдера-Мида и симплексного метода.

Таблица 1.

Исходные данные для индивидуальных заданий

№ варианта	Целевая функция R(X)
	(x₁² - 1) +(x₂⁴- 3) + 4 * (x₃² + 5)
	3 * (x₁⁴ - 1) + 2 * (x₂⁴ - 2) + (x₃⁶ - 3)
	3(x₁² - 4) + 5 (x₂⁴ + 3) + 7 * (2 * x₃² + 5)
	(3 * x₁² - 3) + 4 * (2 * x₂² + 4 * x ) + (x + 3) ?
	3 * ( 2 * x₁⁴ + 1) + 5 * (x₂² + 3) + 4 * (x₃² - 4)
	0.5 * (8 * x₁⁴ - 32) + 16 * (3 * x₂² - 0.9) + 4 * (5 * x₃² - 1)
	2.5 * (2 * x₁² - 1) + 4.8 * (x₂² + 5) + 12 * (x₃⁴ - 2)
	15 * (10 * x₁² + 2) + 8 * (6 * x₂⁴ - 15) + 3 * (12 * x₃² + 6)
	21 * (14 * x₁⁴ + 2.8) + 33 * (8 * x₂² - 4) + 77 * (25 * x₃⁶ - 0.25)
	3 * (12 * x₁⁴ - 0.6) + 4 * (20 * x₂² + 0.2) + (17 * x₃² - 3.4)
	1.3 * (4 * x₁² - 1.6) + 2.5 * (12 * x₂² + 4.8) + (40 * x₃⁴ - 1.6)
	6 * (8 * x₁² - 1) + 7 * (10 * x₂⁴ - 4) + (4 * x₃² - 1.4)
	8 * (9 * x₁⁴ - 7.2) + 7.5 * (4 * x₂⁶ - 4) + 7 * (6 * x₃² - 4.2)
	5 * (x₁² - 10) + 12 * (x₂⁴ + 9) + (x₃² - 1)
	(x₁² - 5) + 8 * (4 * x + x ) + (x + 16) ?
	25 * (3 * x₂² - 6 * x₁² ) + (2 - 4 * x₁² )
	(x₂² - 2 * x₁⁴ ) + (10 – x₁² )
	(3 * x₂² - 6 * x₁² ) + 16 * (8 - 4 * x₁⁴ )

ЛАБОРАТОРНАЯ РАБОТА N 14

БЕ3ГРАДИЕНТНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ

ЦЕЛЬ РАБОТЫ: – определить координаты точки экстремума целевой функции использованием метода покоординатного спуска и метода Хука-Дживса;

доказать, что найденный экстремум является глобальным;

– сопоставить эффективность использованных методов. Вид целевой функции выбирается в соответствии с вариантом задания по таблице.

1. ОПИСАНИЕ МЕТОДИКИ РАСЧЕТОВ

При решении конкретной задачи оптимизации прежде всего необходимо выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. В настоящее время для решения задач оптимизации разработано большое число методов, которые можно разделить на два класса - аналитические и численные. Численные методы поиска экстремума функции используются в тех случаях, когда в точке экстремума отсутствуют производные или целевую функцию (R) сложно либо невозможно продифференцировать.

В практике решения задач оптимизации для нелинейных целевых функций широко используются методы нелинейного программирования. Эти методы могут быть охарактеризованы как многошаговые методы или методы последовательного улучшения исходного (или начального) решения, причем обычно заранее нельзя сказать, какое число шагов гарантирует нахождение оптимума с заданной точностью. Кроме того, выбор величины шага в значительной мере определяет эффективность того или иного метода.

Большинство методов нелинейного программирования использует идею движения в n-мерном пространстве в направлении оптимума. При этом из некоторого исходного или промежуточного состояния Х^(k) осуществляется переход в следующее состояние Х^(k+1) изменением вектора Х^(k) на величину ΔХ^(k), называемую шагом, т.е.

Х^(k+1) = Х^(k)+ ΔХ^(k) (4.1)

Очевидно, что для случая поиска оптимума, являющегося минимумом, для удачно выбранного шага должно выполняться условие:

R(Х^(k+1)) < R(Х^(k)) (4.2)

В противном случае переход в состояние Х^(k+1) нецелесообразен. В значительной части методов шаг, т.е. его величина и направление, определяется как некоторая функция предыдущего состояния Х^(k)

ΔХ^(k)= ΔХ^(k)( Х^(k)) (4.3)

Методы нелинейного программирования в соответствии со способом определения шага можно разделить на три группы: градиентные, безградиентные и методы случайного поиска.

Ниже приведены 2 метода поиска экстремума целевой функции, относящиеся к группе безградиентных методов, - метод покоординатного спуска и метод Хука-Дживса.

1.1. Метод покоординатного спуска

При решении задач оптимизации методом покоординатного спуска поиск экстремума целевой функции осуществляется поочередным изменением каждой независимой переменной до достижения частного экстремума целевой функции. Каждая независимая переменная при фиксированном значении остальных переменных варьируется до тех пор, пока на данном направлении не будет найден экстремум целевой функции. Затем, зафиксировав найденные значения целевой функции и независимой переменной, переходят к варьированию другой независимой переменной, где вновь отыскивается частное значение экстремума и т.д.

При выборе стратегии поиска экстремума по направлению можно использовать любой из методов поиска экстремума функции одной переменной (метод одномерного сканирования, метод локализации экстремума, метод "золотого сечения" и др.). В соответствии с (4.1) координаты следующей точки определяются по следующим выражениям:

X_i^(k+1)= X_i^(k)+ h_i (4.4)

X_j = const (j = 1, 2, 3, 4, 5, ... n), (4.5)

где n - число независимых переменных; h_i - приращение i-ой независимой переменной (шаг).

В (4.4) величина шага h может меняться как по величине, так и по знаку. По мере приближения к точке экстремума для улучшения сходимости величину шага рекомендуется уменьшать.

Алгоритм поиска точки экстремума методом покоординатного спуска следующий:

1) Для задания начальной точки рассчитывается целевая функция.

2) Выбирается одна из независимых переменных и направление поиска по данному направлению.

3) Для выбранной переменной задается шаг приращения h и рассчитывается новое (k+1)-е значение переменной по (4.4).

4) В полученной точке находится значение целевой функции.

5) В случае удачного шага (например, при поиске минимума должно выполняться условие (4.2)), новый шаг делается в том же направлении.

6) В случае неудачного шага следует изменить знак h на противоположный и вернуться к последней из удачных точек.

7) Запоминается значение целевой функции и независимой переменной в данной точке.

8) Меняется направление поиска и аналогичным образом производится поиск локального экстремума по другой независимой переменной.

9) Поиск продолжается до тех пор, пока точка экстремума не будет определена с заданной точностью.

1.2. Метод Хука-Дживса.

Данный метод поиска точки экстремума целевой функции является более эффективным по сравнению с методом покоординатного спуска. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которым в случае успеха следует поиск по образцу. Алгоритм метода следующий.

1. Выбирается начальная базисная точка b₁ и шаг h_i для каждой переменной X_j (j = 1, 2, ..., n). Можно использовать и одинаковый шаг h для всех переменных, однако указанная выше модификация может оказаться полезной.

2. Исследующий поиск проводится с целью получения сведений о локальном поведении целевой функции в окрестности базисной точки. Эти сведения в дальнейшем будут использованы для нахождения направления поиска по образцу.

2.1. Вычисляется значение целевой функции R(b₁) в базисной точке (b₁).

2.2. Каждую независимую переменную по очереди измененяем на величину шага. Таким образом, вычисляется значение целевой функции R(b₁+h₁.e₁), где e₁ - единичный вектор в направлении оси x. Если это приводит к уменьшению целевой функции в случае поиска минимума, то b₁ изменяют на b₁+h₁.e₁.

В противном случае вычисляется значение функции R(b₁–h₁.e₁), и если ее значение уменьшилось, то b₁ заменяют на b₁–h₁.e₁. Если ни один из проделанных шагов не приводит к уменьшению значения целевой функции, то точка b₁ остается неизменной и рассматриваются изменения в направлении оси X2, т.е. находят значение функции R(b₁+h₂.e₁) и т.д. Когда будут рассмотрены все n переменных, то получим новую базисную точку b₂.

2.3. Если b₂=b₁, т.е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b₁, но с уменьшенной величиной шага. На практике удовлетворительным считается уменьшение величины шага (шагов) в десять раз от начальной длины.

2.4. Если b₂≠b₁, то производится поиск по образцу.

3. При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура выполняется таким образом:

3.1. Разумно двигаться из базисной точки b₂ в направлении b₂–b₁, поскольку поиск в этом направлении уже привел к уменьшению значения целевой функции. Точка образца может быть вычислена следующим образом:

P₁ = b₁ + 2 (b₂-b₁) (4.6)

В общем случае:

P_i = b_i + 2 (b_i+1-b_i) (4.7)

3.2. Проводится исследование в окрестностях точки P=(P_i).

3.3. Если наименьшее значение на шаге 3.2 меньше значения в базисной точке b₂(в общем случае b_i+1), то получают новую базисную точку b₃ (b_i+2), после чего следует повторить шаг 3.1. В противном случае не производится поиск по образцу, а заменяется базисная точка. В качестве новой базисной точки выбирается та точка, в которой на предыдущем шаге значение целевой функции было минимальным. Затем выполняется исследование вокруг новой базисной точки.

4. Процесс поиска завершается, когда длина шага (длины шагов) станут меньше заданного малого значения. Ниже приведена блок-схема данного метода (рис. 1), блок-схема этапа 3 приведена на рис. 2.

2.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Работа выполняется в такой последовательности:

· на диске Z в директории \LABS\ находят программу ortimize.exe и выполняют с ее помощью расчеты на ЭВМ согласно своего индивидуального задания, в результате которых определяют координаты точки экстремума целевой функции;

· осуществляют проверку - является ли найденный экстремум глобальным, для чего расчеты повторяются несколько раз из начальных точек с различными координатами. Ввод исходных данных в программе организован в диалоговом режиме. Поэтому для запуска необходимо использовать управляющий модуль ortimize.exe. В качестве исходных данных вводятся вид целевой функции, координаты начальной точки, начальный шаг, величина приращения.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.

В табл. 4.1. приведены целевые функции и область допустимых изменений исследуемых независимых переменных. Требуемая точность определения координат точки экстремума 0,001.

ОФОРМЛЕНИЕ ПРОТОКОЛА.

В протоколе по лабораторной работе описываются результаты расчетов, выполненных на ЭВМ, приводятся доказательства нахождения глобального экстремума.

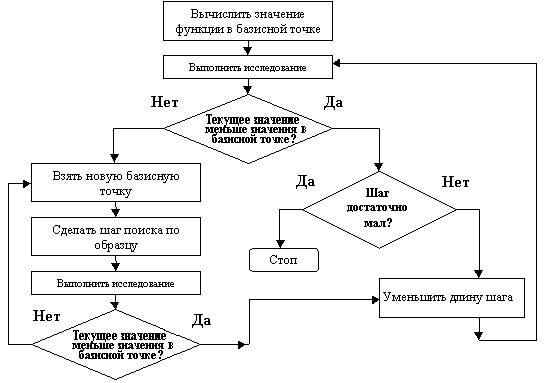
Рис.1. Блок-схема метода Хука-Дивса.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Классификация методов решения задач оптимизации.

2. Общая идея методов нелинейного программирования.

3. Метод покоординатного спуска, алгоритм расчета.

4. Составить блок-схему метода покоординатного спуска.

5. Метод Хука-Дживса, алгоритм расчета.

6. Общая блок-схема метода Хука-Дживса.

7. Блок-схема поиска в базисной точке.

8. Как доказать, что найденный экстремум является глобальным?

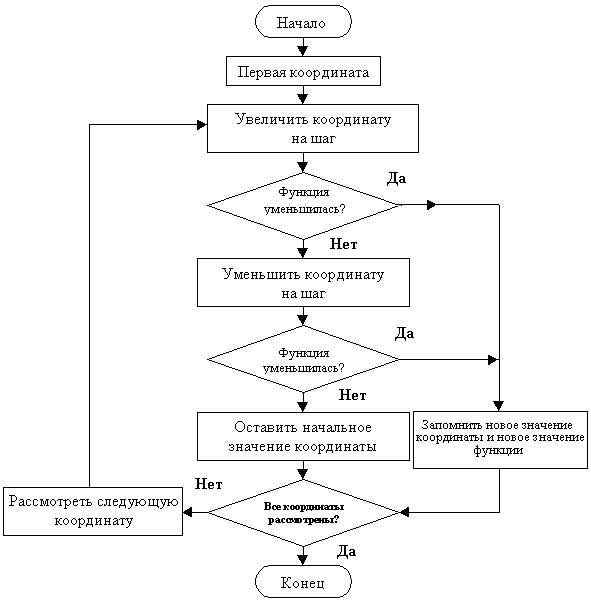
Рис.2. Блок-схема этапа "Выполнить исследование"

Исходные данные для индивидуальных заданий

Таблица 4.1

№ варианта	Целевая функция R(X)
	(x₁² - 1) +(x₂⁴ - 3) + 4 * (x₃² + 5)
	3 * (x₁⁴ - 1) + 2 * (x₂⁴ - 2) + (x₃⁶ - 3)
	3(x₁² - 4) + 5 (x₂⁴ + 3) + 7 * (2 * x₃² + 5)
	2 2 4 (3 * x - 3) + 4 * (2 * x + 4 * x ) + (x + 3) ????????????????? 1 1 2 3
	3 * ( 2 * x₁⁴ + 1) + 5 * (x₂² + 3) + 4 * (x₃² - 4)
	0.5 * (8 * x₁⁴ - 32) + 16 * (3 * x₂² - 0.9) + 4 * (5 * x₃² - 1)
	2.5 * (2 * x₁² - 1) + 4.8 * (x₂² + 5) + 12 * (x₃⁴ - 2)
	15 * (10 * x₁² + 2) + 8 * (6 * x₂⁴ - 15) - 3 * (12 * x₃² + 6)
	21 * (14 * x₁⁴ + 2.8) + 33 * (8 * x₂² - 4) + 77 * (25 * x₃⁶ - 0.25)
	3 * (12 * x₁⁴ - 0.6) + 4 * (20 * x₂² + 0.2) + (17 * x₃² - 3.4)
	1.3 * (4 * x₁² - 1.6) + 2.5 * (12 * x₂² + 4.8) + (40 * x₃⁴ - 1.6)
	6 * (8 * x₁² - 1) + 7 * (10 * x₂⁴ - 4) + (4 * x₃² - 1.4)
	8 * (9 * x₁⁴ - 7.2) + 7.5 * (4 * x₂⁶ - 4) + 7 * (6 * x₃² - 4.2)
	5 * (x₁² - 10) + 12 * (x₂⁴ + 9) + (x₃² - 1)
	(x₁² - 5) + 8 * (4 * x + x ) + (x + 16) ??
	25 * (3 * x₂² - 6 * x₁² ) + (2 - 4 * x₁² )
	(x₂² - 2 * x₁⁴ ) + (10 – x₁² )
	(3 * x₂² - 6 * x₁² ) + 16 * (8 - 4 * x₁⁴ )

Лабораторная РАБОТА № 15.

“ГРАДИЕНТНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ оптимизации“

ЦЕЛЬ РАБОТЫ - составить подпрограммы для расчета целевой функции и частных

производных по независимым переменным;

определить координаты точки экстремума целевой функций с

использованием метода градиента и наискорейшего спуска;

доказать, что найденный экстремум является глобальным;

сопоставить эффективность использованных методов.

Вид целевой функции выбирается в соответствии с вариантом задания

лабораторной работы №5 по табл. 5.1

Среди методов, применяемых для решения задач оптимизации методами нелинейного программирования, значительное место занимают методы поиска решения, основанные на анализе производных оптимизируемой функции.

Предполагается в дальнейшем, что анализируются только непрерывные дифференцируемые функции R(U).

В градиентных методах используется следующее свойство градиента целевой функции - вектор градиента по направлению совпадает с направлением наискорейшего возрастания целевой функции. Поэтому движение к точке экстремума производится по направлению градиента целевой функции (при поиске максимума), а в случае поиска минимума – в противоположном направлении.

1.1. Метод градиента

Поиск экстремума при использовании метода градиента осуществляется

в два этапа. На первом находятся значения частных производных по всем

н

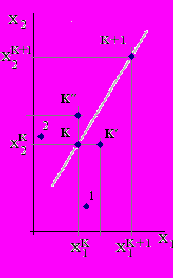езависимым переменным и определяется направление градиента в рассматриваемой точке. На втором этапе осуществляется шаг в выбранном направлении.

Для определения направления градиента необходимо найти значения частных производных к по независимым переменным. Если неизвестен аналитический вид целевой функции R(U) и он достаточно прост, то вычисления производных dR/dX_j чаще всего не составляет особого труда. В противном случае для нахождения производных dR/dX_j используется численный метод, при котором для вычисления производный проводится вспомогательная серия расчетов. Ниже рассмотрен случай, когда целевая функция зависит от двух независимых переменных (рис.1). Около выбранной точки К с координатами( Х₁^К , Х₂^К ) ставятся две вспомогательные течки: К’- на расстоянии е₁ вдоль оси Х₁; К” - на расстоянии е₂вдоль оси Х₂. Здесь е₁ и е₂ -

Рис.1 достаточно малые приращения независимых переменных. В этих точках - К’ с координатами (Х₁^К+е₁; Х₂^К) и К” с координатами (Х₁^К; Х₂^К+е₂)-рассчитываются значения целевой функции. Так же рассчитывается значения целевой функции в исходной точке К с координатами (Х₁^К; Х₂^К)

Частные производные целевой функции пo независимым переменным находятся по следующим формулам:

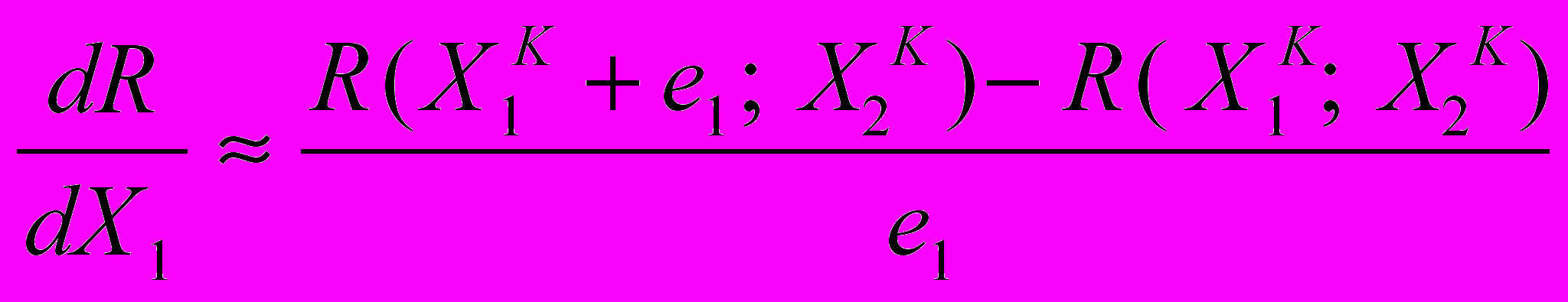(6.1)

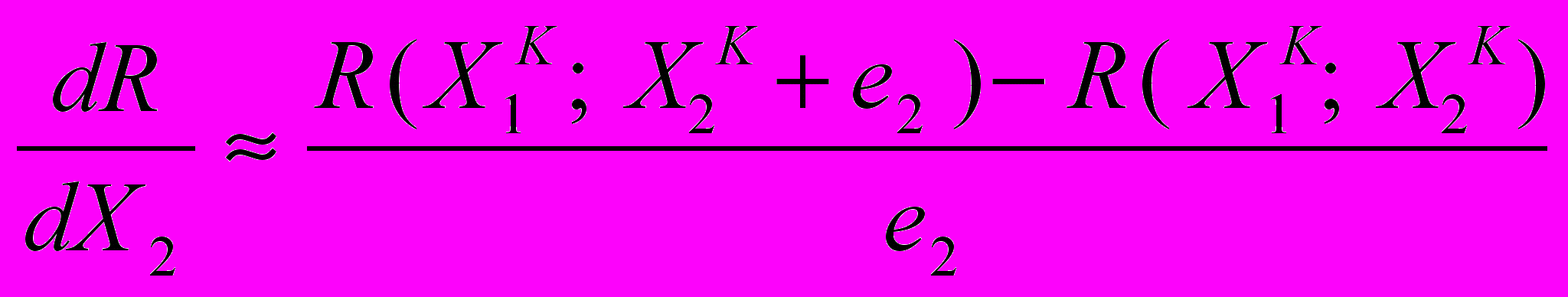(6.2)

В данной работе величина шага Х_j⁽^k⁾определяется следующим образом:

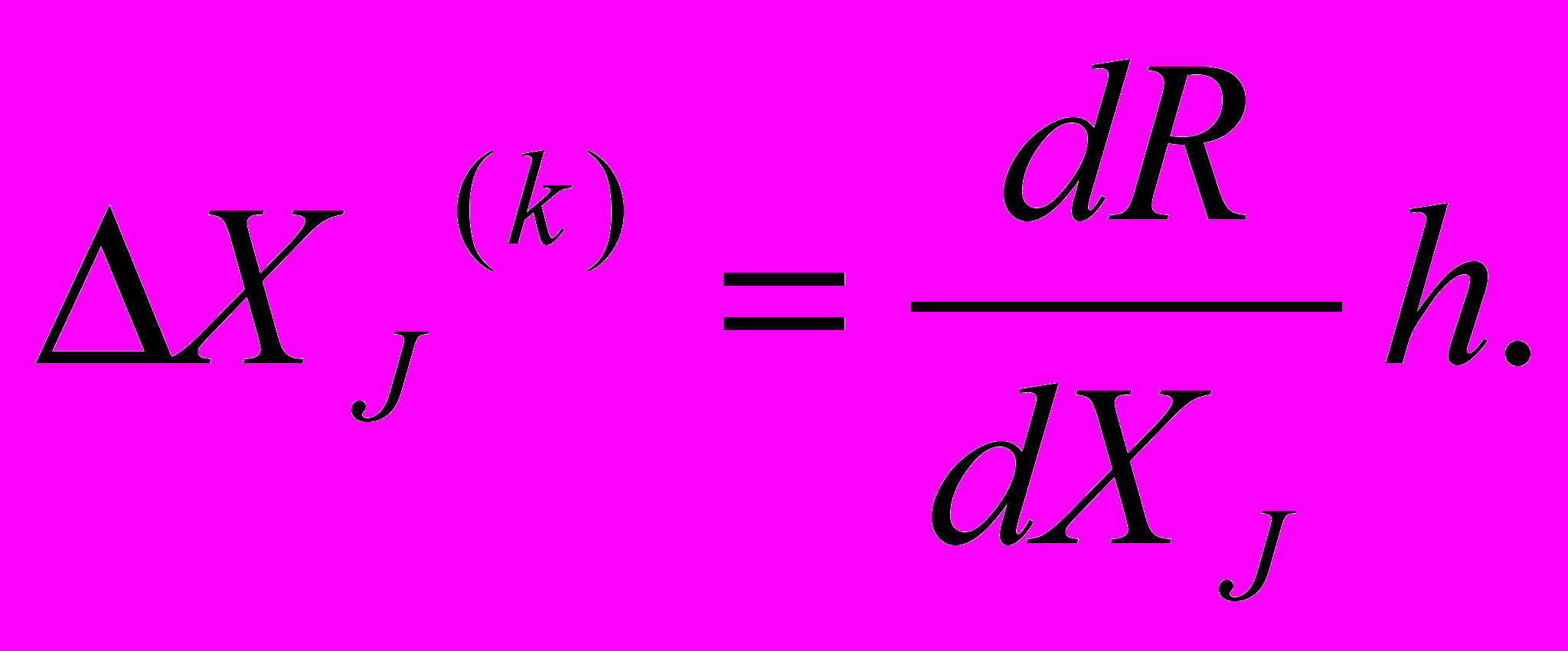, (6.3)

где h - шаг поиска.

Величина приращения Х_j независимой переменной X_J при постоянном значении

h изменяется автоматически в соответствии с изменением абсолютной величины градиента, что является достоинством данного алгоритма.

Координаты (К+1)- ой точки определяются следующим образом:

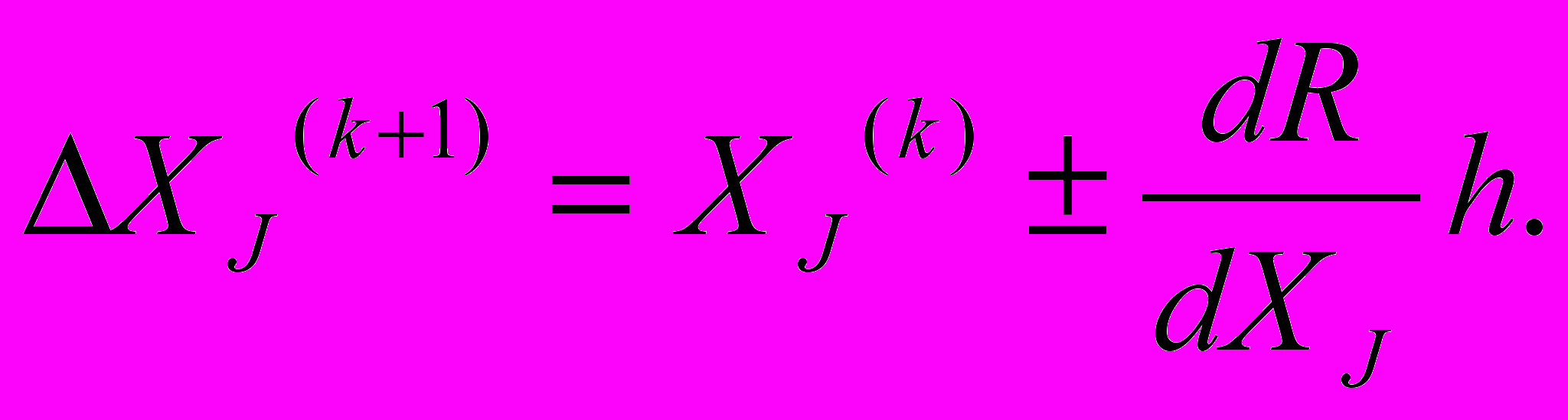(6.4)

В (6.4) при поиске максимума целевой функции ставиться знак «+», а при поиске минимума – знак «-».

Во вновь найденной (К+1)- ой точке рассчитывается значение целевой функции.

В случае удачного шага находиться новое значение градиента и делают новый

шаг и т.д. В случае неудачного шага в точке К снова определяют значение градиента, например, при изменённых значениях h либо е.

Поиск продолжают до тех пор, пока не будет определена точка экстремума с заданной точностью.

Блок - схема программы, реализующей метод градиента, приведена на рис.2

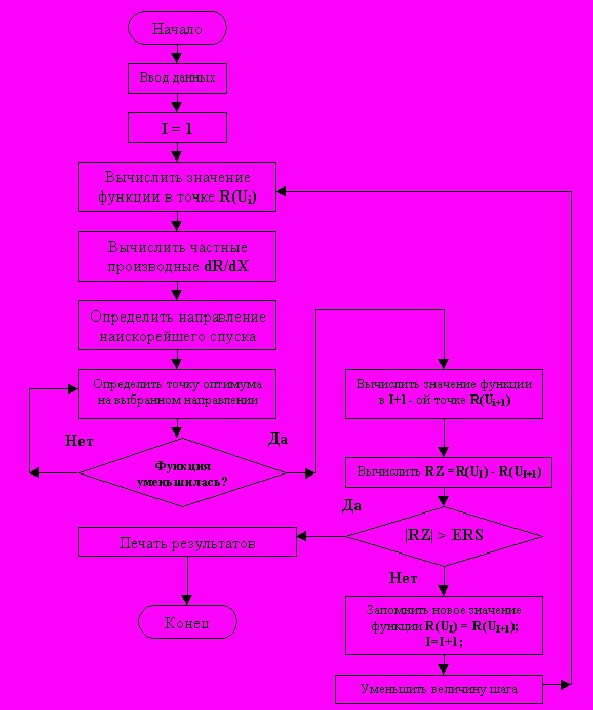
1.2 Метол наискорейшего спуска

Метод наискорейшего спуска, объединяющий основные идеи методов релаксации и градиента, заключается в следующем. В исходной точке определяется градиент оптимизируемой функции и тем самым направление ее наискорейшего убывания. Затем вдоль этого направления делается не один шаг, как в методе градиента, а продолжается движение до нахождения частного экстремума вдоль этого направления. Затем в точке экстремума вновь определяют градиент и осуществляется движение в выбранном направлении до частного экстремума и т.д. до тех пор пока не будет найден абсолютный экстремум.

Сравнение методов градиента, релаксации, наискорейшего спуска позволяет заметить, что в методе наискорейшего спуска сочетаются достоинства методов градиента и релаксации. Метод наискорейшего спуска позволяет найти экстремум при минимальном объёме вычислений. Метод особенно выгодно использовать в том случае, когда градиент функции изменяется не резко. Очевидно, что вблизи экстремума метод наискорейшего спуска вырождается в метод градиента, в качестве критерия окончания поиска можно использовать те же критерии, что и в методе градиента.

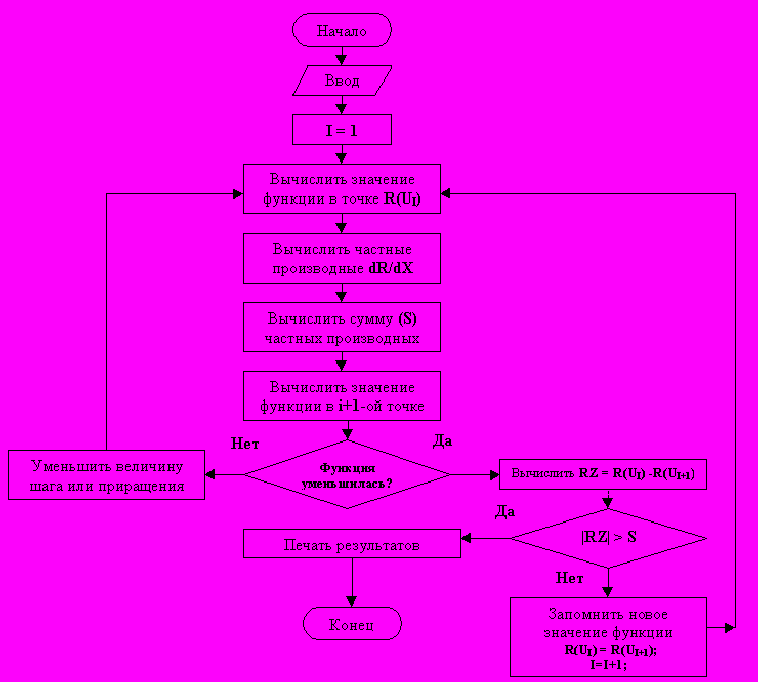
Рис.2. Блок-схема метода градиента

Blog