Методические указания к лабораторным работам по курсу "Математическое моделирование и применение ЭВМ в химической технологии " (часть 2) для студентов 4 курса химико-технологического факультета / Сост.

Вид материала

Рис.2.7 Рис.2.8
Индивидуальные задания
Оформление протокола
Исходные данные вариантов расчета
Контрольные вопросы
Лабораторная работа 11
1. Описание методики расчетов
1.1. Определение оптимального времени пребывания
1.2. Определение оптимального времени пребывания

Подобный материал:

1 2 3 4 5 6

Рис.2.7 Рис.2.8

Аналогичным образом строятся статические характеристики при варьировании других параметров.

Н

еобходимо отметить следующее. Выше были рассмотрены случаи, когда возможно существование в реакторе нескольких стационарных режимов. В том случае, если существует единственный стационарный режим, то вид статических характеристик изменяется.

Построение статических характеристик проводится следующим образом. Выбирается исходный стационарный режим. Затем при варьировании одного из входных параметров определяются новые стационарные режимы. Статические характеристики строятся, как правило, в координатах Δθвых = f(Δaвх),

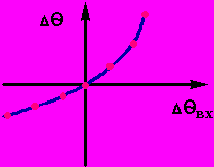
где aвх - параметр на входе. В качестве примера на рис.2.9 приведена статическая характеристика Рис.2.9

по каналу: Δθ = f(Δθ_вх)

Исследование статических характеристик в любом реакторе необходимо, во-первых, для предсказания поведения объекта при изменении условий на входе во-вторых, для выбора канала управления, т.е. такого параметра, которым можно варьировать, чтобы осуществлять процесс в заданных условиях при возможных флуктуациях входных параметров.

При выборе канала управления необходимо, чтобы:

1.Изменение параметра на входе оказывало заметное влияние на выходные параметры.

2. Выбранный канал управления должен быть наименее инерционным, т.е. время, в течение которого параметр на выходе отреагирует на изменение входного параметра, должно быть минимально возможным.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Исходные данные, необходимые для расчетов, приведены в табл.1. Номер варианта соответствует порядковому номеру фамилии студента по журналу.

ОФОРМЛЕНИЕ ПРОТОКОЛА

В протоколе по лабораторной работе формулируется цель работы, приводятся полученные безразмерные параметры, диаграмма тепловыделение –теплоотвод для базового варианта и при варьировании входных параметров, статические характеристики по исследованным каналам управления.

Таблица 1

ИСХОДНЫЕ ДАННЫЕ ВАРИАНТОВ РАСЧЕТА
№	Параметры процесса									Диапазон варьирования
№	Со	(-ΔH)	E	K₃₂₃	F	α	Твх	Тх	Vo	ΔΘ_вх	Δγ	Δ(ΔΘ_ад)
1	5.5	179.8	84.2	0.0155	6.0	41.9	287	295	0.1	-4 /+2	-0.2/+0.5	-4 / +6
2	7.1	104.8	103.5	0.023	2.5	50.3	282	291	0.05	-3 /+2	-0.2/+0.3	-6 / +5
3	4.5	142.9	126.1	0.027	1.0	62.9	285	288	0.025	-4 /+3	-0.2/+0.5	-5 / +5
4	3.5	160.9	151,7	1,226	6,0	41,9	281	286	0,1	-6 /+3	-0.2/+0.4	-4 / +6
5	3.7	122.3	174.7	3.68	2.5	50.3	282	284	0.05	-6 /+2	-0.2/+0.5	-6 / +6
6	2.5	178.0	189.4	4.0	1.0	62.9	274	283	0.025	-4 /+4	-0.2/+0.6	-6 / +5
7	4.0	92.6	206.6	6.44	1.5	41.9	279	282	0.025	-5 /+3	-0.2/+0.5	-5 / +5
8	6.2	199.5	84.2	0.0155	16	21.0	274	295	0.1	-4 /+4	-0.3/+0.5	-8 / +6
9	6.8	142.0	103.5	0.023	5.0	33.5	283	291	0.05	-5 /+3	-0.3/+0.5	-6 / +6
10	5.8	132.0	126.1	0.027	8.0	10.5	283	288	0.025	-5 /+2	-0.3/+0.5	-6 / +6
11	3.9	172.6	151.7	1.226	10	33.5	277	286	0.1	-4 /+3	-0.2/+0.5	-6 / +6
12	2.4	220.8	174.7	3.68	12	14.0	276	284	0.05	-4 /+2	-0.2/+0.4	-4 / +6
13	3.1	161.3	189.4	4,0	5,0	16,8	275	283	0,025	-6 /+3	-0.3/+0.5	-6 / +6
14	4.2	115,2	206,6	6,44	10	8,4	281	282	0,025	-7 /+2	-0.2/+0.5	-6 / +6
15	5.8	189,2	84,2	0,0155	11	26,7	279	295	0,1	-3 /+4	-0.2/+0.4	-5 / +5
16	6.9	122,0	103,5	0,023	3,8	38,6	282	291	0,05	-4 /+5	-0.2/+0.5	-4 / +6
17	5.3	136.3	126.1	0.027	4,5	16,3	284	288	0,025	-5 /+3	-0.3/+0.4	-6 / +6
18	3.7	166,1	151,7	1,226	9,0	32,6	278	286	0,1	-4/+4	-0.2/+0.5	-5 / +5
19	3.2	148.5	174.7	3.68	7.3	20.0	275	284	0.05	-5 /+2	-0.2/+0.3	-4 / +4
20	2.8	171.1	189.4	4.0	3.9	18.8	274	283	0.025	-4 /+3	-0.1 /+0.4	-7 / +6
21	4.1	106.4	206.6	6.44	5.8	12.6	280	282	0.05	-4 /+4	-0.2/+0.4	-6 / +6
22	6.1	191.7	84.2	0.0155	14	22.5	275	293	0.025	-3 /+3	-0.2/+0.5	-7 / +7

Размерность величин:

Со – моль/м³; (-ΔH) – кДж/моль; Е – кДж/моль; К₃₂₃ – 1/с; F - м²;

α – Вт/м².К; Твх – К; Тх – К; Q – м³/с.

Общие данные для всех вариантов:

Vp = 5 м³; Toп = 273 K; Cp = 5000 Дж/(кг.К); ρ = 1.676 кг/м³.

КОНТРОЛЬНЫЕ ВОПРОСЫ

Характер зависимости скорости реакции от температуры на примере реакции первого порядка.
Модель реактора идеального смешения и ее основные особенности.
Уравнение энергетического баланса РИС в безразмерной форме.
Построение диаграммы тепловыделение – теплоотвод, условия существования стационарного режима.
Устойчивость, основные понятия. Условие устойчивости, границы и запас устойчивости.
Определение числа и характера стационарных режимов (на основании диаграммы тепловыделение – теплоотвод).
Статические характеристики, их применение, метод построения. Параметрическая чувствительность.
Доказать, что при изменении температуры входа и прочих неименных параметрах линии теплоотвода параллельны друг другу.

Определить координаты «центра вращения при изменении параметра теплоотвода».

ЛАБОРАТОРНАЯ РАБОТА 11

РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ С ИСПОЛЬЗОВАНИЕМ

АНАЛИТИЧЕСКИХ МЕТОДОВ

ЦЕЛЬ РАБОТЫ: - определить оптимальное время пребывания и максимальную концетрацию целевого продукта В для двух последовательных реакций первого порядка А  B  D в реакторе идеального вытеснения;

- получить выражения для определения оптимального времен пребывания и максимальной концентрации целевого продукта В для тех же реакций в реакторе идеального смешения;

- сравнить показатели, достигаемые в РИС и РИВ;

- для обратимой экзотермической реакции А ↔ В построить оптимальный температурный режим для заданных значений параметров.

1. ОПИСАНИЕ МЕТОДИКИ РАСЧЕТОВ

Аналитические методы, основанные на классических методах математического анализа, используются в задачах, у которых целевая функция имеет аналитическое выражение, а число переменных невелико. Задача оптимизации формулируется следующим образом. Существует процесс, известна его математическая модель и установлен критерий оптимальности R в виде функции

R = R(X, U) (1)

где X - вектор входных параметров, U - вектор управляющих параметров. Заданы ограничения: X_min ≤ X_доп ≤ X_max; U_min ≤ U_доп ≤ U_max. При заданных ограничениях необходимо найти такие значения U, при которых R достигает экстремума.

Необходимое условие существования экстремума функции одной переменной формулируется следующим образом: в точках экстремума производная dR(U)/dU либо обращается в нуль, либо не существует. Достаточное условие существования экстремума - если вторая производная меньше нуля, то в данной точке существует максимум, если вторая производная больше нуля, то в данной точке существует минимум, если вторая производная равна нулю, то необходимо исследовать производные высших порядков. Необходимым условием существования экстремума функции многих переменных является равенство нулю частных производных первого порядка по всем переменным.

1.1. Определение оптимального времени пребывания

для двух последовательных реакций в РИВ

Для двух последовательных реакций АВD необходимо определить оптимальное время пребывания t_опт, при котором выход целевого продукта В будет достигать максимума.

Пусть a - начальная концентрация компонента А. В начальный момент времени концентрации компонентов В и D равны нулю, т.е. при t = 0: C_B = C_D = 0;

Критерии оптимизации: выход целевого продукта R = C_B/ а

Управляющее воздействие - время пребывания t.

Пусть обе реакции протекают по первому порядку. Скорости реакций описываются следующими выражениями:

W1 = K1.Ca (2)

W2 = K2.Cв (3)

Изменение концентрации компонента В во времени:

dCв/dt = W1 - W2 (4)

Из (2) найдем выражение для текущей концентрации С_A. Преобразуем (2):

-dС_A / dt = K1. С_A; d С_A / С_A = -K1.dt

Проинтегрировав, получим:

ln(С_A /a) = -K1.t; или С_A = a.exp(-K1.t) (5)

Подставим (5) и (3) в (4), получим:

dCв/dt = K1.a.exp(-K1.t) - K2.Cв

или

dCв/dt + K2.Cв = K1.a.exp(-K1.t) (6)

Решив полученное уравнение, найдем выражение для определения

текущей концентрации компонента В:

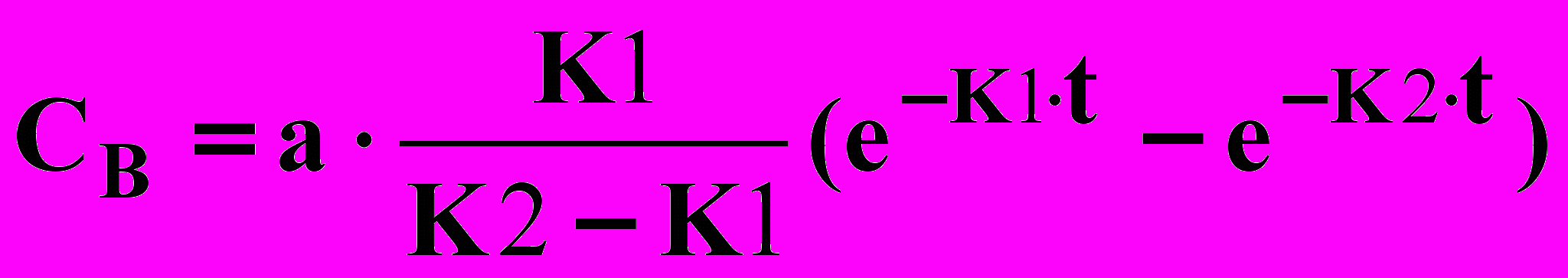(7)

Выход целевого продукта

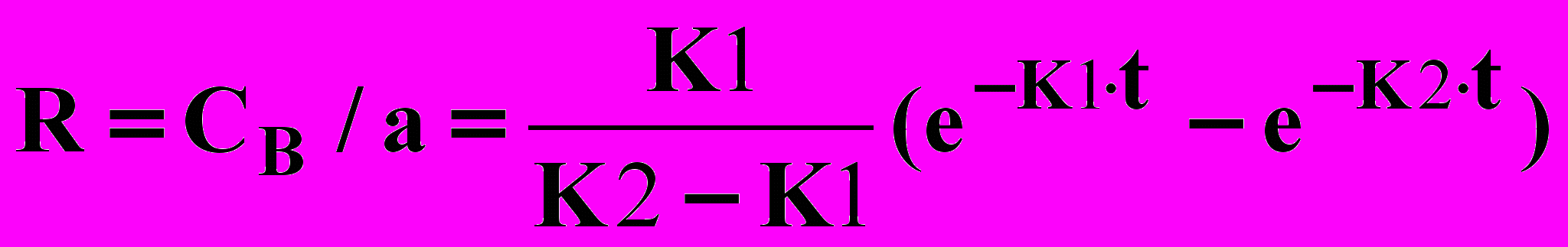(8)

Исследуем экстремум полученной целевой функции (8). Условия существования максимума dR/ dt = 0; d²R/ dt² < 0.

Найдем первую производную и приравняем ее нулю:

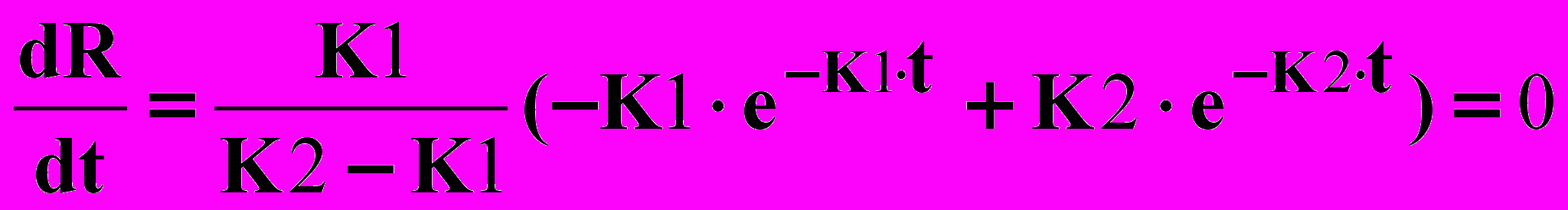(9)

Решив полученное уравнение , определим оптимальное время пребывания:

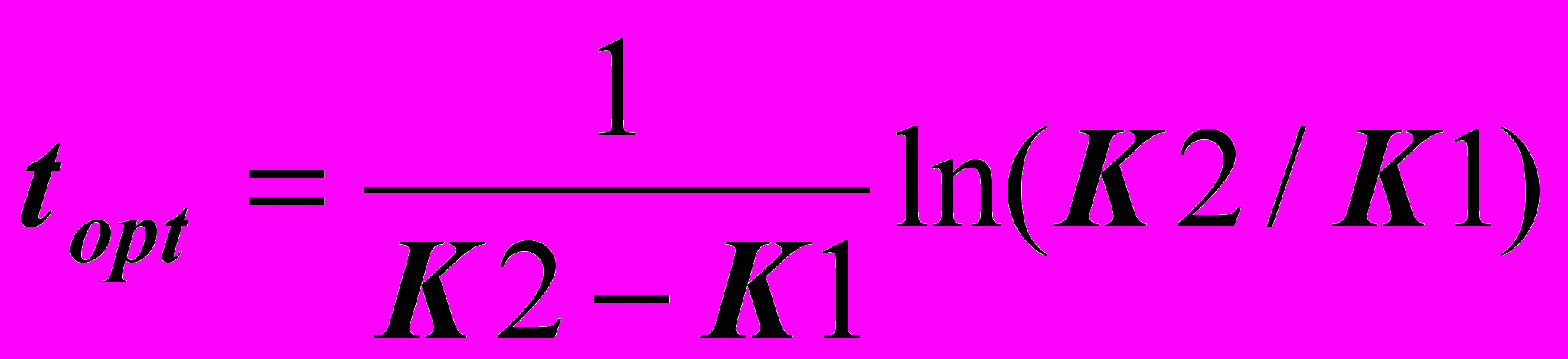(10)

Для проверки выполнения достаточного условия существования максимума вычисляем вторую производную:

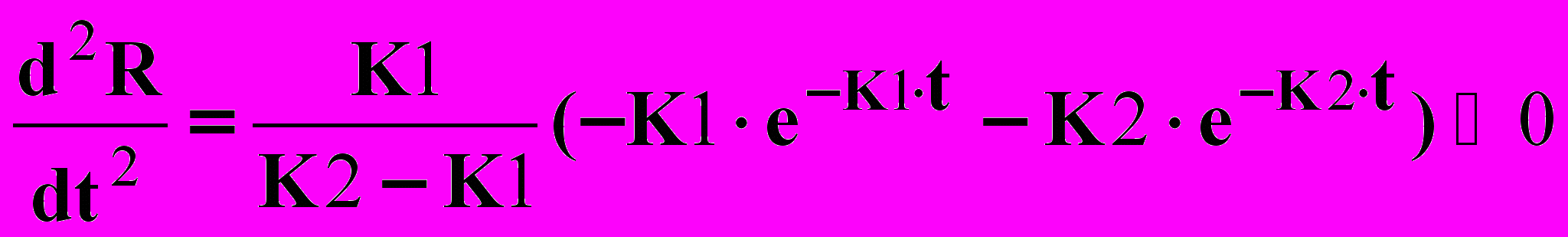(11)

Так как вторая производная меньше 0, то в данной точке существует максимум целевой функции R.

Подставив (10) в (7), получим выражение для определения максимальной концентрации компонента В:

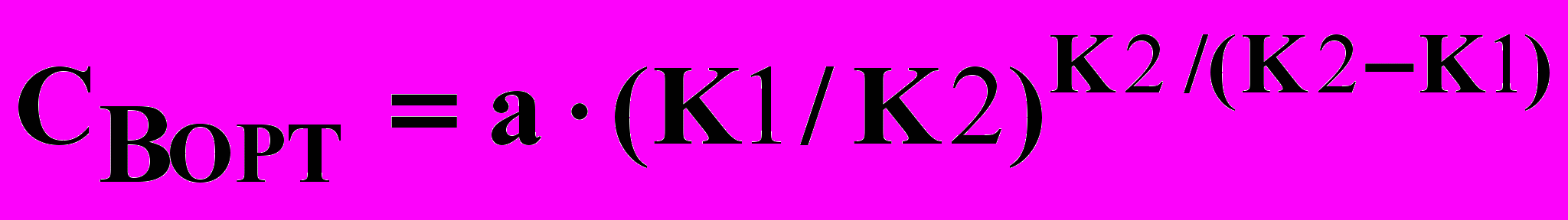(12)

Исходные данные для расчетов берутся из табл.1.1. Необходимо вычислить для заданных значений параметров оптимальное время пребывания и максимальную концентрацию целевого продукта В для двух последовательных реакций первого порядка А  B  D в реакторе идеального вытеснения.

1.2. Определение оптимального времени пребывания

для двух последовательных реакций в РИС

Для аналогичных предыдущему примеру условий протекания реакций материальный баланс по компонентам А и В в реакторе идеального смешения имеет вид:

Q.( C_Ao - C_A) - V.K1.C_A = 0; (13)

-Q.C_B + V.(K1. C_A - K2.C_B) = 0;

Разделив оба уравнения на расход реагентов V, получим:

C_Ao - C_A - t.K1. C_A= 0; (14)

- C_B + t.(K1. C_A- K2.C_B) = 0;

где t = V/Q - среднее время пребывания реагентов в реакторе.

На основании уравнений (14) следует записать выражение для критерия оптимальности, приняв в качестве последнего выход целевого продукта В. Управляющим параметром является среднее время пребывания реагентов в реакторе.

Используя необходимое условие существования экстремума продифференцировав полученное выражение по времени пребывания и приравняв его к нулю - получить выражение для определения оптимального времени пребывания. Исходные данные для расчетов берутся аналогично предыдущему примеру (табл.1.1). Необходимо вычислить для заданных значений параметров оптимальное время пребывания и максимальную концентрацию целевого продукта В для двух последовательных реакций первого порядка АBD в реакторе идеального смешения и сравнить аналогичные показатели, достигаемые в РИС и РИВ.

Blog

Рис.2.7 Рис.2.8

ИСХОДНЫЕ ДАННЫЕ ВАРИАНТОВ РАСЧЕТА

Δγ