Методические указания к лабораторным работам по физике по практикуму «Вычислительная физика» для студентов специальности 010701 «Физика» тогу

Вид материала

Методические указания

Содержание Компьютерная обработка экспериментальных данных §1. Погрешности измерений Промахи (или грубые погрешности Случайные ошибки всегда присутствуют в эксперименте. Расчет случайной погрешности в прямых измерениях §2 Графическое представление результатов измерений §3 Метод наименьших квадратов. Постановка задачи приближения функции по методу наименьших квадратов. ПРИМЕР. Приближение функции по методу наименьших квадратов Расчет случайной погрешности средствами Excel Лабораторная работа 1: Компьютерная обработка экспериментальных данных (2 часа). Используемуе формулы Результат расчета §2. Вычисление определенных интегралов. Лабораторная работа 2: Распределение Максвелла. Лабораторная работа 3

Подобный материал:

• Учебно-методический комплекс по дисциплине Молекулярная физика для специальности 010701, 480.43kb.
• Учебно-методический комплекс по дисциплине Физика Конденсированного Состояния Для специальности, 322.8kb.
• Методические указания к лабораторным работам №1-­5 для студентов специальности 210100, 363.6kb.
• Методические указания к лабораторным работам для студентов специальности 210100 "Автоматика, 536.56kb.
• Государственным Образовательным Стандартом (гос) для обязательного изучения студентами, 200.98kb.
• Рабочая программа по курсу «Применение лазеров в науке и технике» для специальности, 219.45kb.
• Программа по дисциплине «Экономика» гэс р. 11 по специальности 010701 «Физика», 456.82kb.
• Учебно-методический комплекс по дисциплине Оптика для специальности 010701 "Физика", 561.69kb.
• Рабочая программа по философии для специальности 010701 «Физика» гсэ. Ф. 10. Физический, 485.77kb.
• Методические указания к лабораторным работам Самара 2007, 863.04kb.

Федеральное агентство по образованию

Государственное образовательное учреждение
высшего профессионального образования

«Тихоокеанский государственный университет»


Вычислительная физика

(практикум на ЭВМ)

Методические указания к лабораторным работам по физике по практикуму «Вычислительная физика» для студентов специальности 010701 «Физика»


ТОГУ

2008

УДК 535.2


Вычислительная физика (практикум на ЭВМ): методические указания к лабораторным работам по физике по практикуму «Вычислительная физика» для студентов специальности 010701 «Физика» / сост. В. В. Насыров. – Хабаровск : Изд-во Тихоокеанского гос. ун-та, 2008. – 8 с.


Печатается в соответствии с решениями кафедры «Физика» и мето­ди­ческого совета факультета математического моделирования и процес­сов управления.


© Тихоокеанский государственный университет, 2008

Компьютерная обработка экспериментальных данных

§1. Погрешности измерений

Введение

Никакие измерения не могут быть абсолютно точными, поэтому при любом измерении, измеренное значение величины всегда отличается от ее истинного значения.

Задачей экспериментатора является не только нахождение самой величины, но и оценка допущенной при измерении погрешности. В зависимости от свойств и причин возникновения различают систематические и случайные погрешности и промахи.

Систематическими называются погрешности, которые при многократных измерениях, проводящихся одним и тем же методом с помощью одних и тех же измерительных приборов, остаются постоянными.

Систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Они соответствуют отклонению измеренного значения от истинного всегда в одну сторону.

Систематические погрешности могут быть обусловлены, во-первых, неисправностью или неправильной работе на используемых приборах (например, неправильной установкой “нуля”). Во-вторых, их причиной может быть несовершенство используемой методики измерения или неучет постоянных факторов, влияющих на исследуемое явление. Например, можно получать завышенные значения температуры плавления кристалла, если проводить измерения при повышенном внешнем давлении.

Помимо погрешностей, возникающих в процессе измерений, систематическими являются погрешности, связанные с применением приближенных формул, и ошибки, обусловленные отличием реального объекта от принятой модели.

Приборной погрешностью называется разность между показаниями любого прибора и истинным значением измеряемой величины. Она может содержать случайную и систематическую составляющие.

Промахи (или грубые погрешности) проявляются обычно в резком отклонении результата отдельного измерения от остальных. Промахи обусловлены главным образом недостаточным вниманием экспериментатора или неисправностями средств измерения. Результаты таких измерений отбрасываются.

Случайными называются погрешности, которые при многократных измерениях в одинаковых условиях изменяются непредсказуемым образом.

Случайные ошибки обусловлены множеством неконтролируемых причин, действие которых неодинаково в каждом опыте. В результате этого при измерении одной и той же величины несколько раз подряд в одинаковых условиях получается целый ряд значений этой величины, отличающихся от истинного значения случайным образом.

Случайные ошибки всегда присутствуют в эксперименте.

Природа случайных погрешностей может быть различной: флуктуации нулевого положения указателя измерительного прибора; несовершенство органов чувств экспериментатора (например, невозможность включить секундомер точно в нужный момент); случайные неконтролируемые изменения внешних воздействий - температуры, влажности, давления; наводки в электрической цепи и т.д., которые практически невозможно учесть.

Расчет случайной погрешности в прямых измерениях

Пусть некоторая величина X измеряется N раз:

.

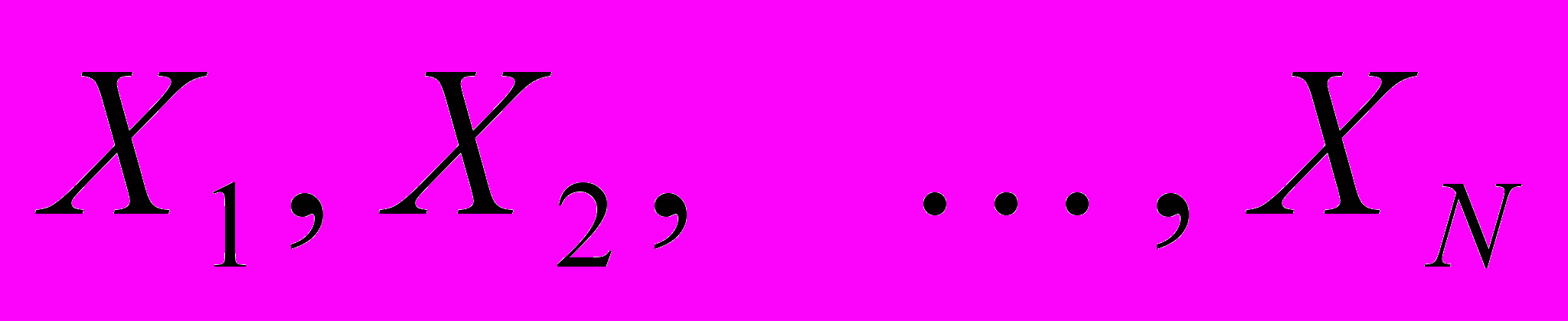Задача обработки экспериментальных данных результатов измерений заключается в определении границы интервала, в котором заключено истинное значение измеряемой величины.

Принята следующая форма записи результата измерений какой-либо величины:

.

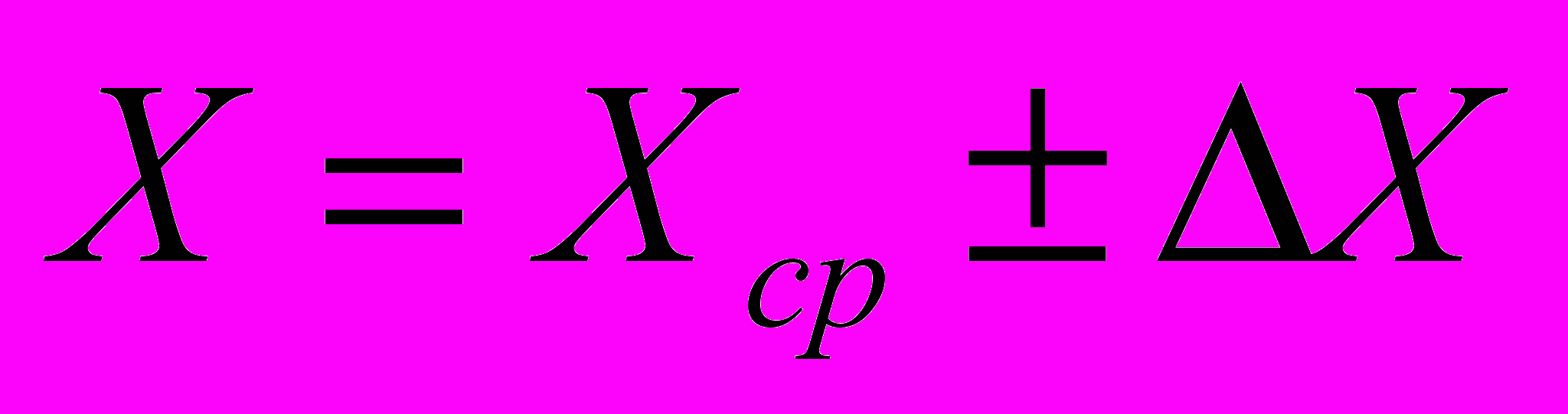За наиболее вероятное значение величины X принимают среднее арифметическое значение результатов измерений:

.

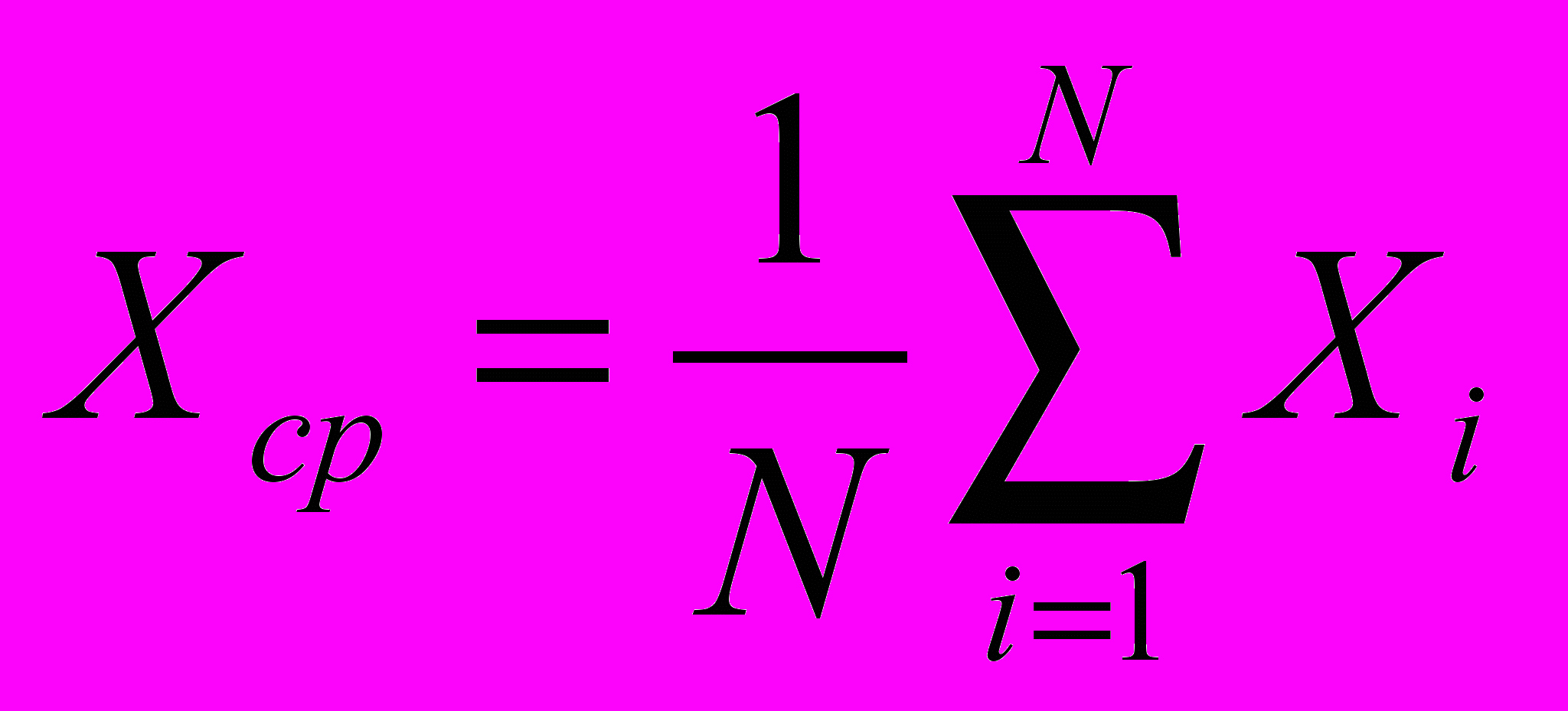Чем больше число измерений, тем ближе среднее значение к истинному.

При наличии в измерениях случайной погрешности, абсолютная погрешность 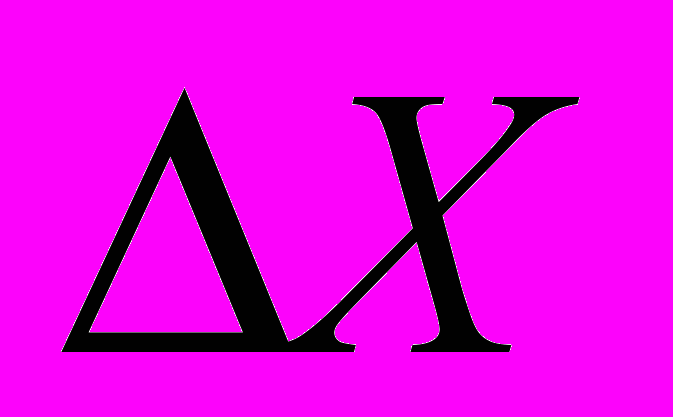по методу Стьюдента определяется следующим образом

,

,

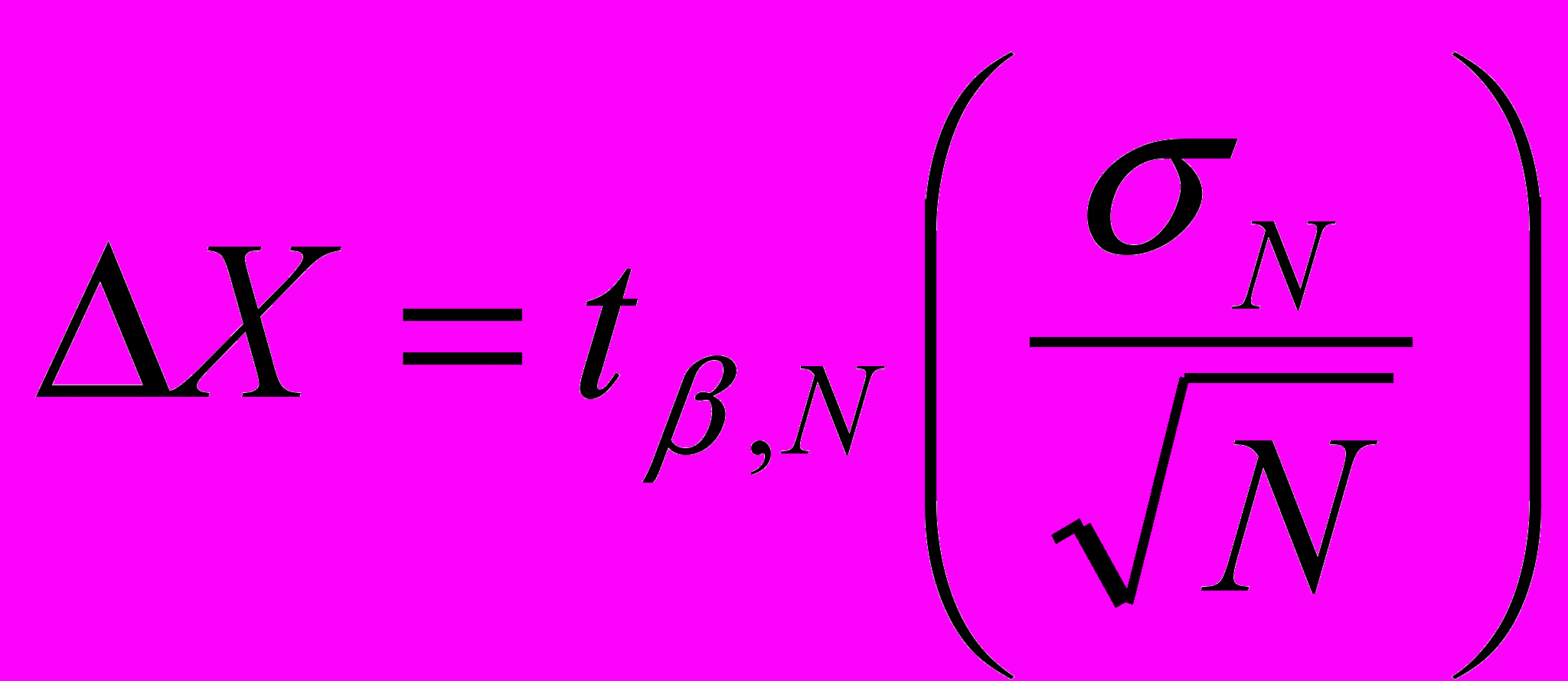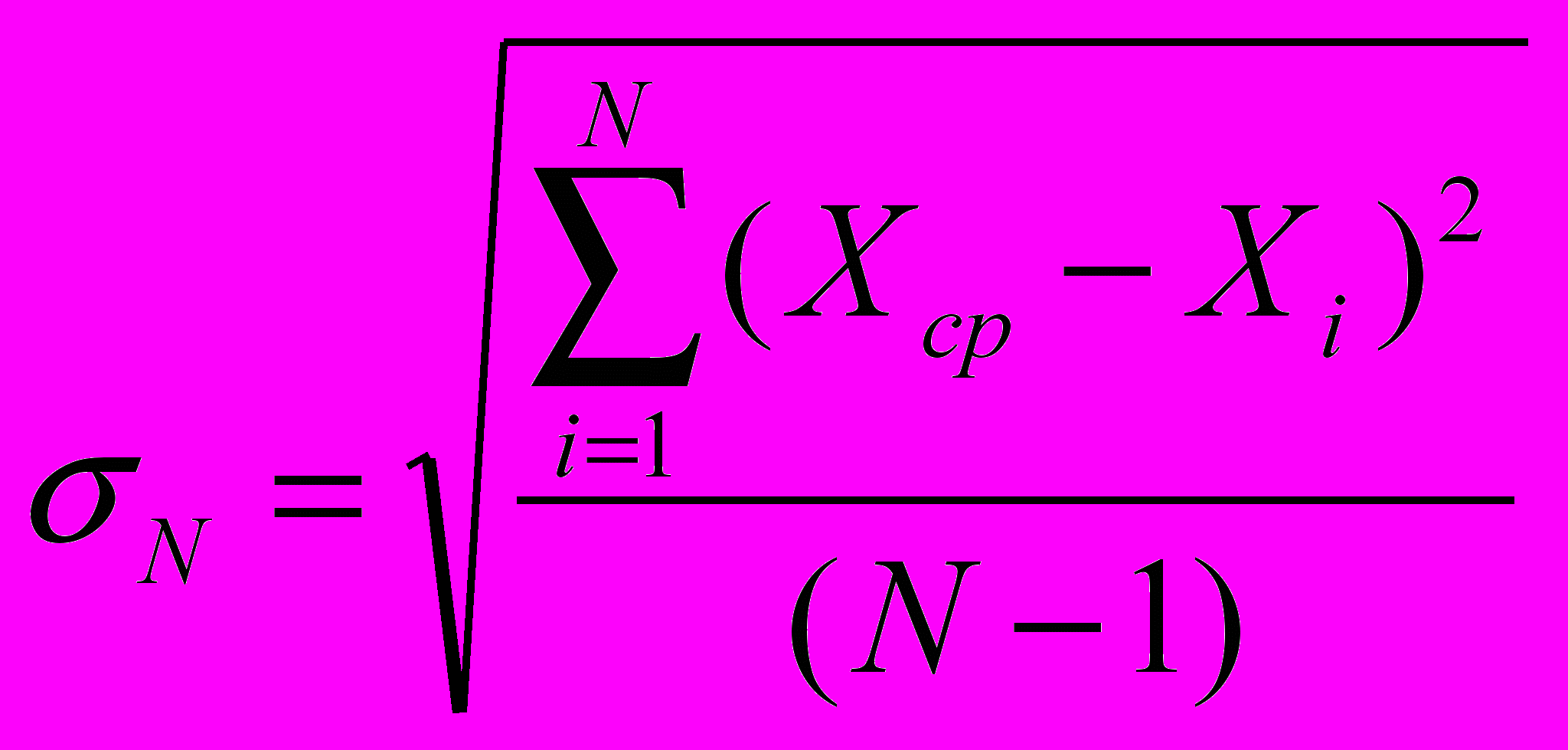где 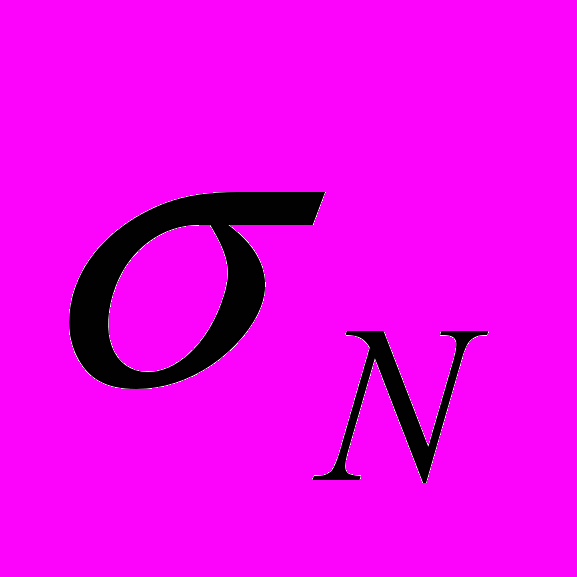– стандартное отклонение, 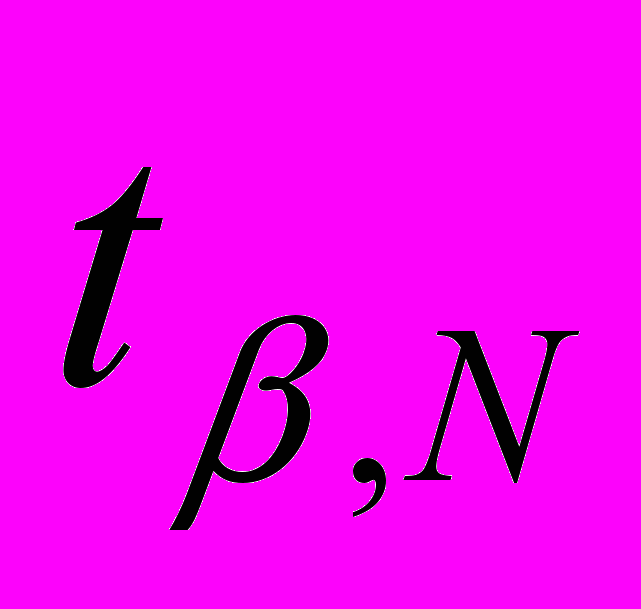– коэффициент Стьюдента, 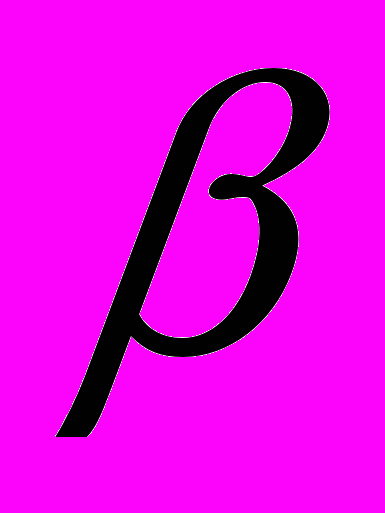– надежность, величина, равная вероятности с которой доверительный интервал включает в себя истинное значение величины X.

Для примера обозначим на числовой оси точками результаты. Они группируются вокруг средней величины 

^{}



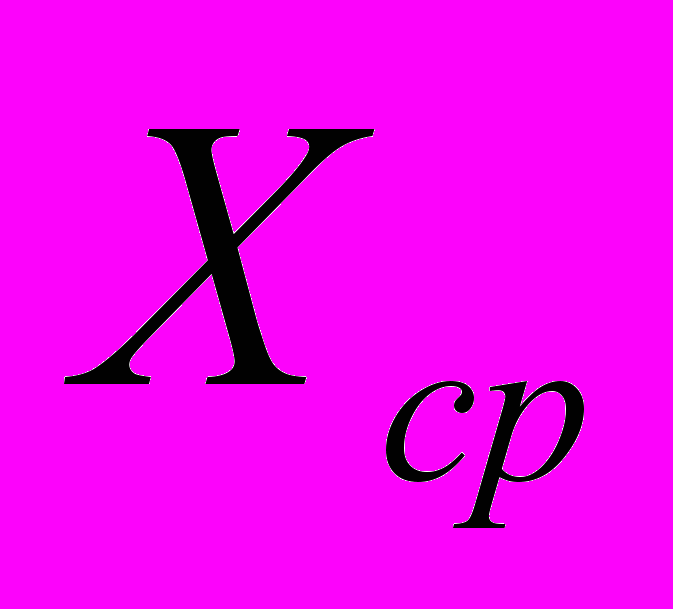
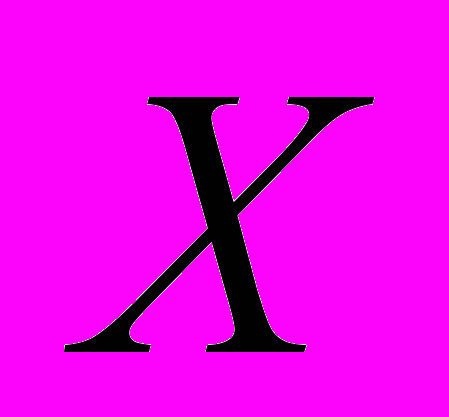
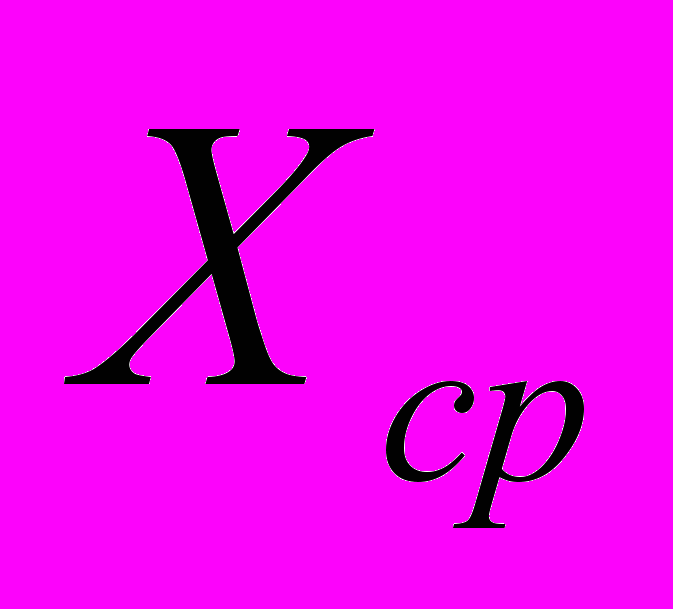
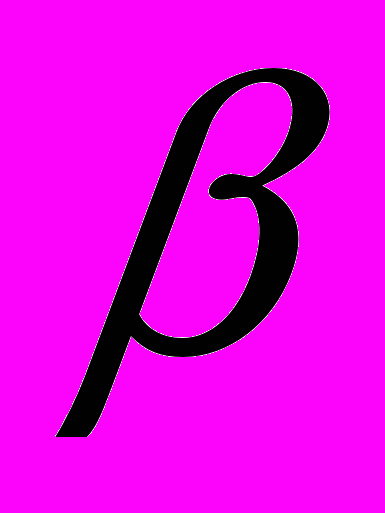
Круглыми скобками обозначим доверительный интервал, внутри которого находятся 5 экспериментальных значений из 10, т.е. доверительная вероятность 0,5. Квадратным скобкам соответствует доверительный интервал для вероятности 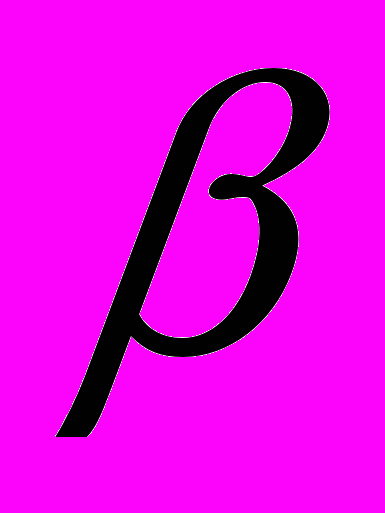0,8.

В лабораториях физического практикума принято значение надежности.

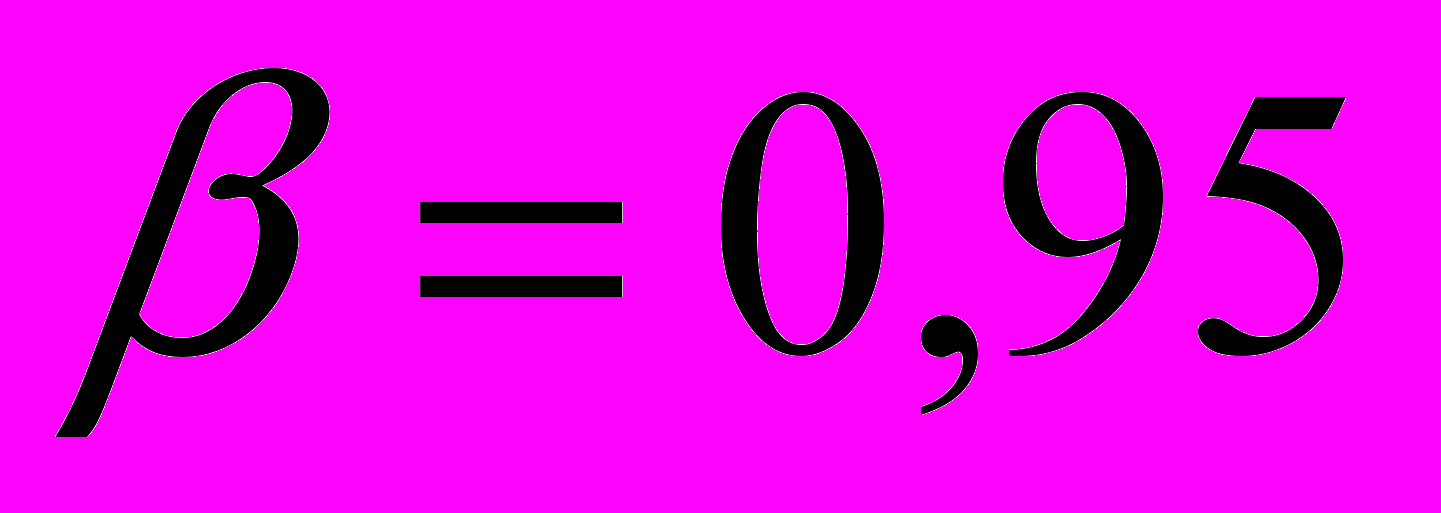Коэффициент Стьюдента 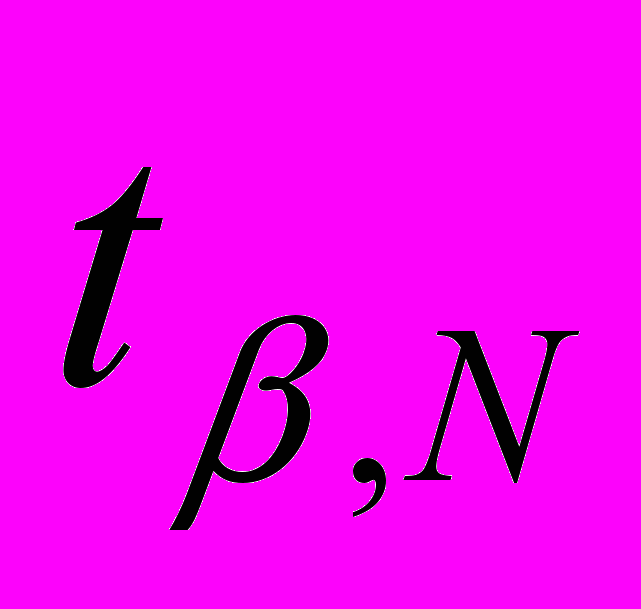является поправочным и применяется для корректировки доверительного интервала при небольшом числе измерений (N<30).

Коэффициент Стьюдента 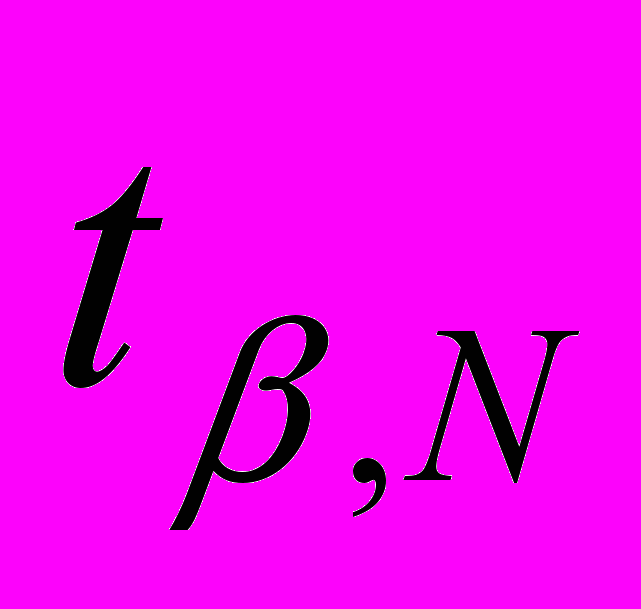может быть рассчитан в рамках теории вероятности.

N	2	3	4	5	6	7	8	9	10	15	20	100	
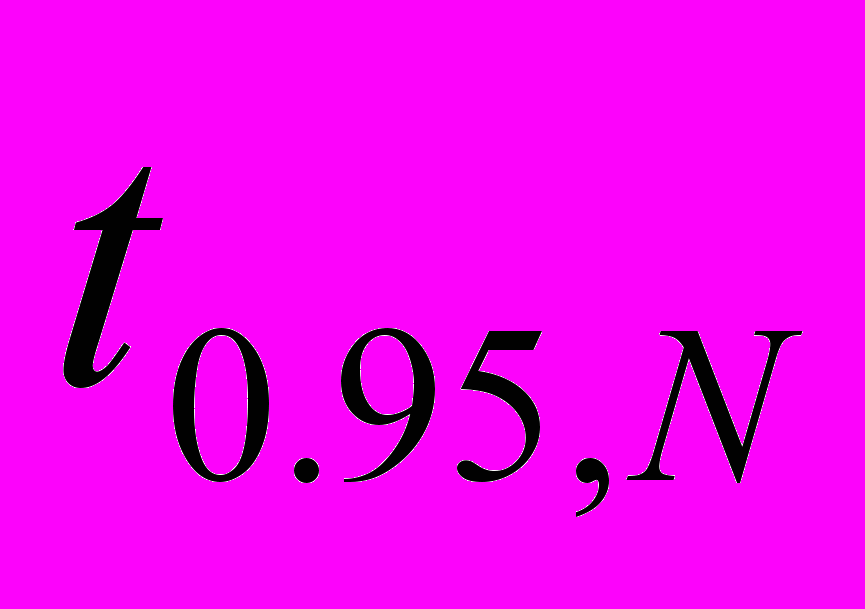
	12.7	4.3	3.2	2.8	2.6	2.4	2.4	2.3	2.3	2.1	2.1	2.0	2.0

Приводимый способ расчета при небольшом (n = 310) числе измерений всегда носит оценочный характер.

§2 Графическое представление результатов измерений

Графики дают возможность наглядного восприятия разного рода функциональных зависимостей в больших массивах данных. При этом через имеющиеся экспериментальные данные можно провести как теоретическую, так и экспериментальную кривые.

При оформлении графиков необходимо выполнять следующие правила.

1. График должен содержать надпись, из которой было бы ясно физическое содержание представленной закономерности.

2. Масштабы и начала отсчета по координатным осям выбираются так, чтобы график изображения зависимости занимал большую часть поля чертежа. При этом на пересечении осей не обязательно должны находиться нулевые значения величин.

Правильно	Неправильно

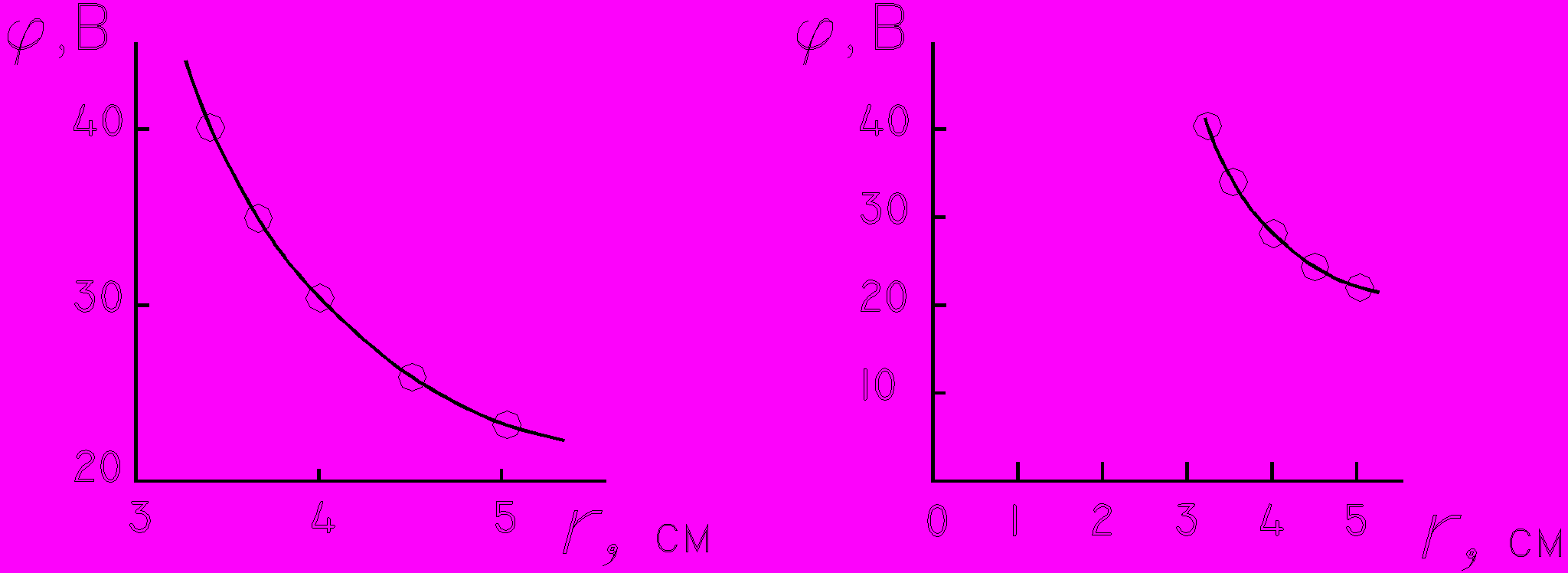3. На осях координат откладываются равноотстоящие друг от друга деления масштаба так, чтобы было удобно работать с графиком. Значения, полученные в эксперименте, не указываются.

Неправильно



Неудачно



Правильно



4. В конце координатных осей обязательно указываются условные обозначения откладываемых величин и, через запятую, их единицы измерения.





6. Экспериментальная кривая проводится плавно через доверительные интервалы всех или большинства экспериментальных точек так, чтобы экспериментальные точки наиболее близко и равномерно располагались с разных сторон кривой.

Правильно	Неправильно

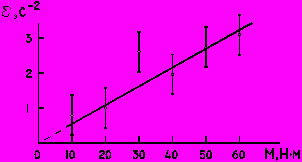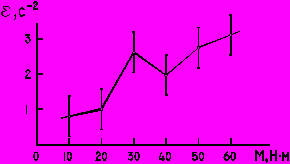§3 Метод наименьших квадратов.

Метод наименьших квадратов (МНК) относится к методам аппроксимации экспериментальных данных, заданных в виде таблицы аналитической зависимостью (кривой).

Метод наименьших квадратов позволяет аппроксимировать данные такой функцией, которая справедлива во всем диапазоне табличных данных, причем кривая не обязательно должна проходить через все точки, но её необходимо провести так, чтобы отклонения кривой от табличных данных были минимальны. Обычно минимизируют сумму квадратов отклонений между значениями функции, определяемыми выбранной кривой и таблицей.

Постановка задачи приближения функции по методу наименьших квадратов.

Пусть функция y=f(x) задана таблицей своих значений: , i=0,1,-n. Требуется найти многочлен

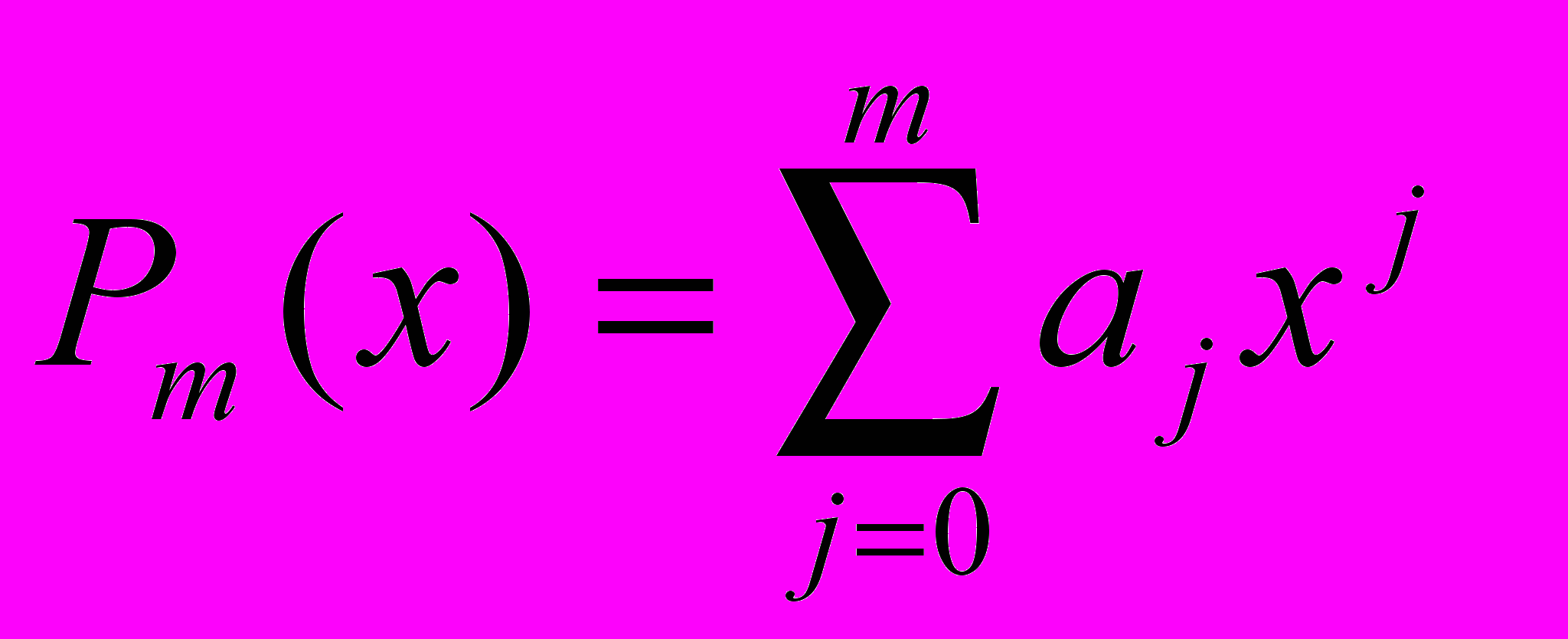, (1)

для которого среднеквадратичное отклонение

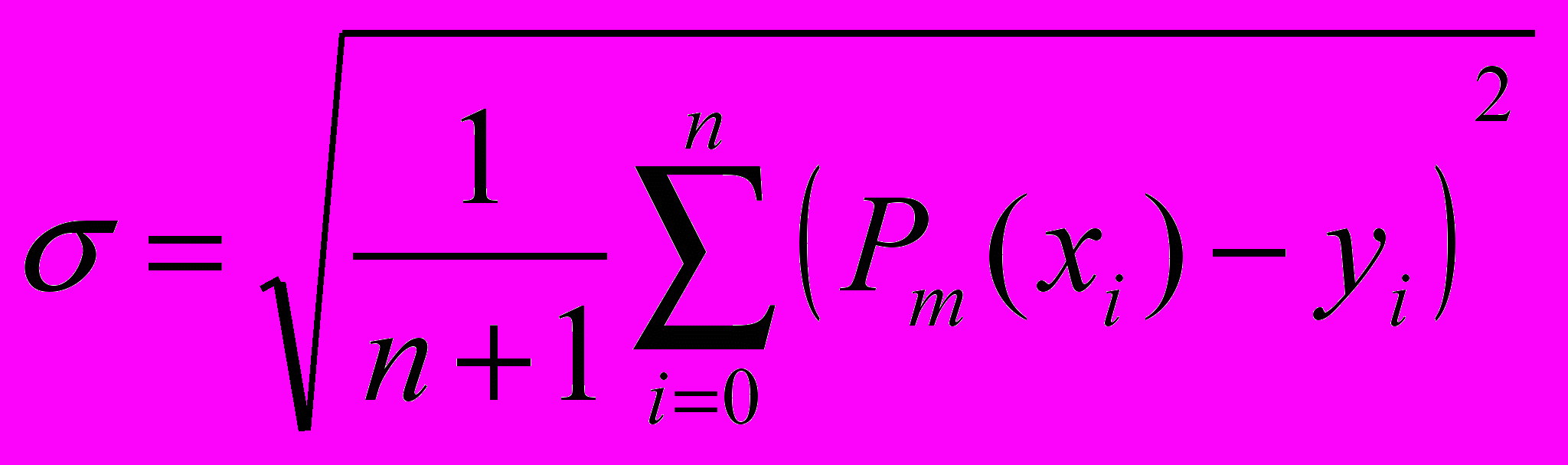(2)

минимально.

То есть, фактически нужно подобрать набор кофициентов 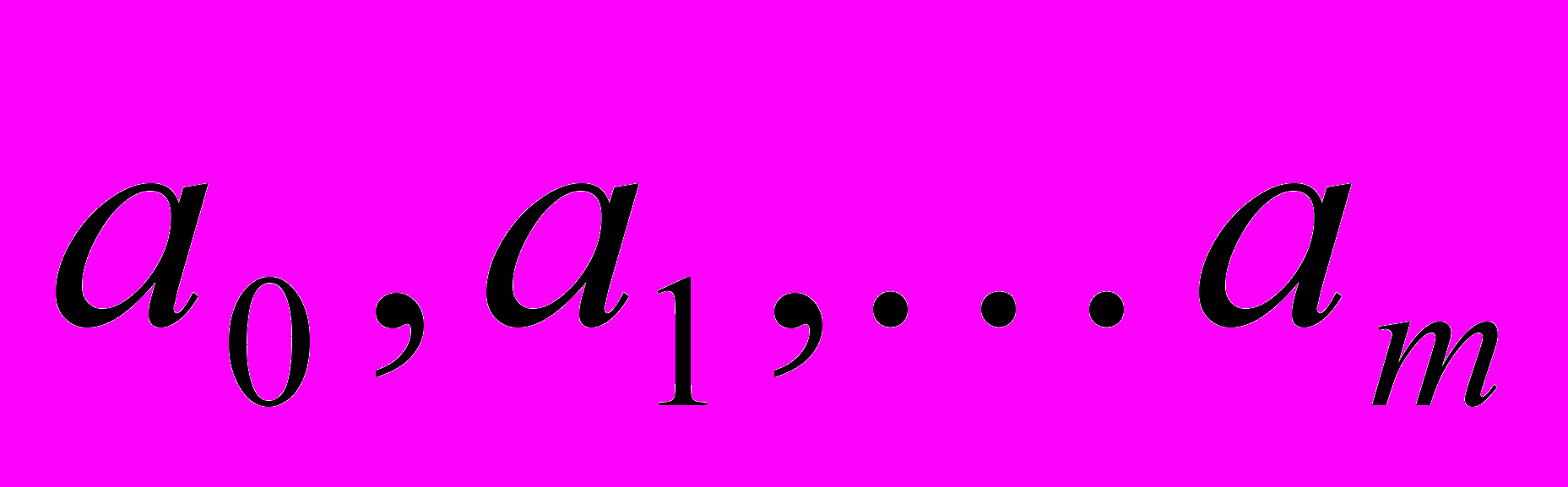, минимизирующий функцию

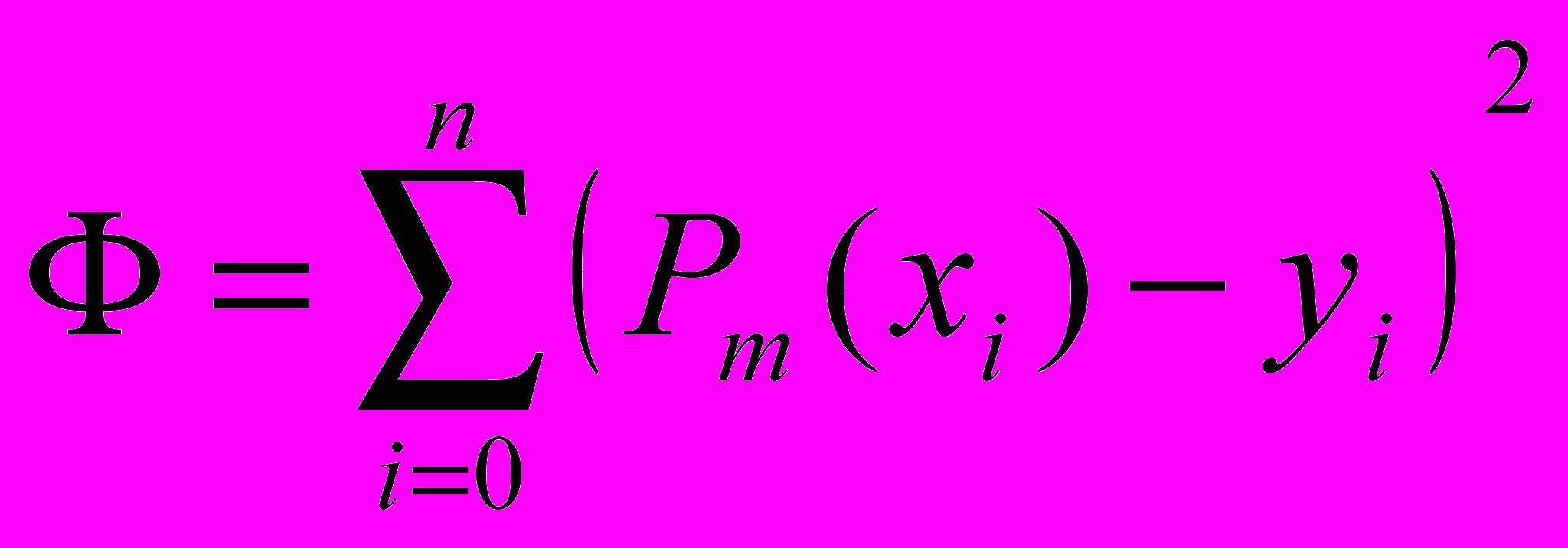. (3)

Используя необходимое условие экстремума,

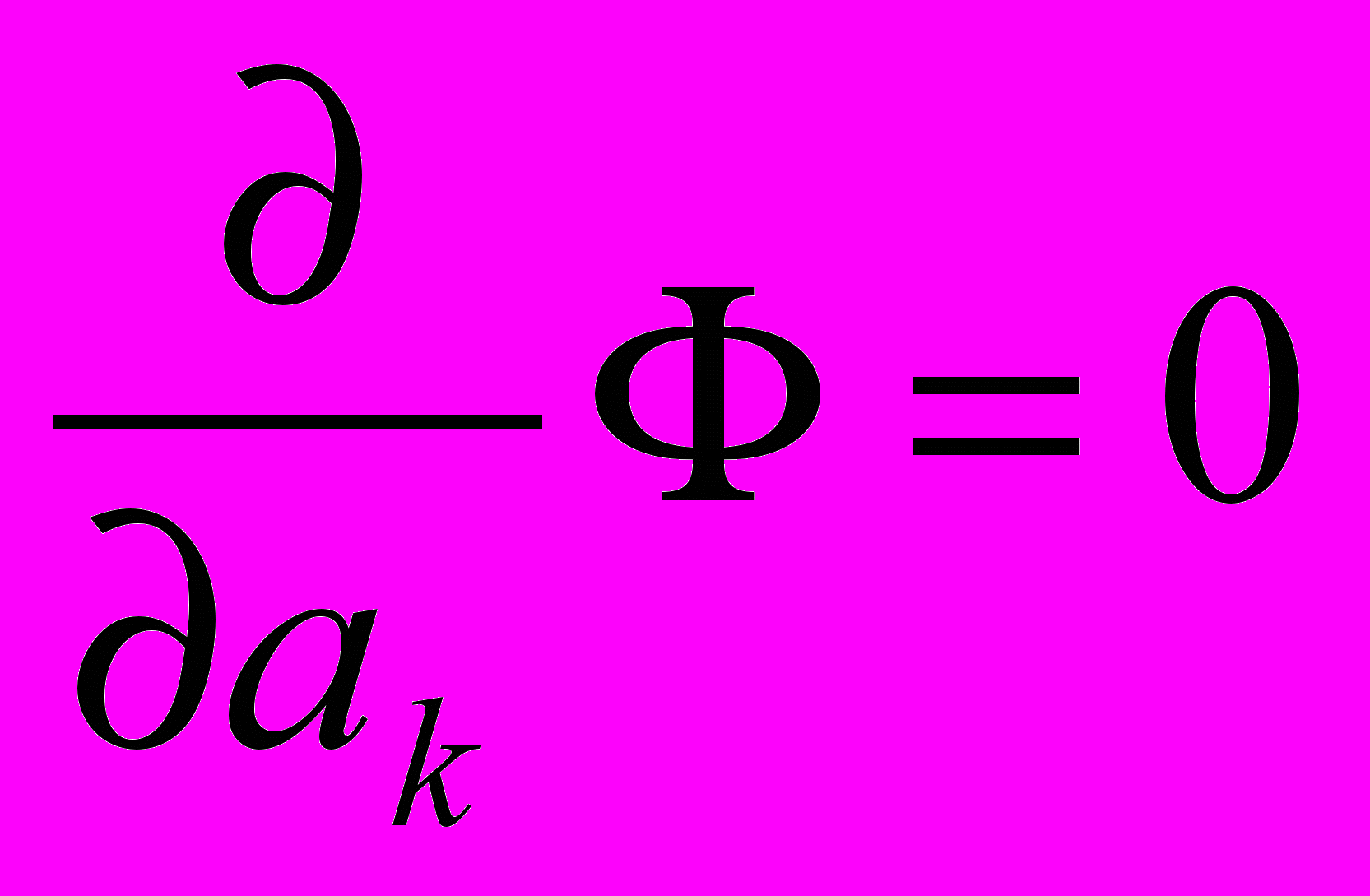, k=0,1,..., m получаем систему метода наименьших квадратов: 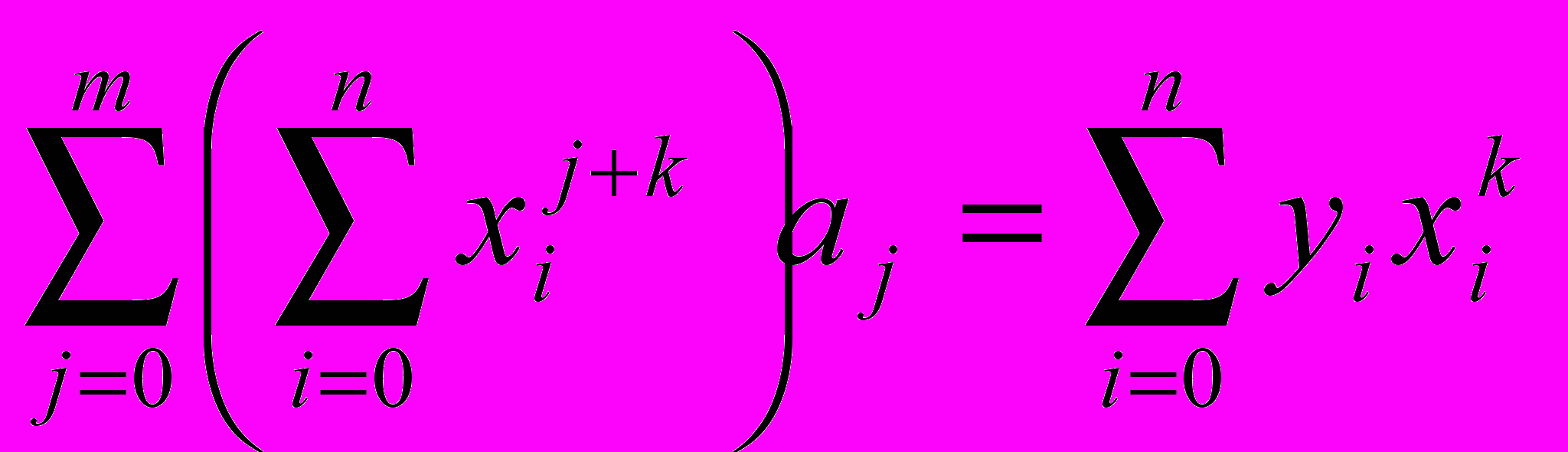, k=0,1,…, m. (4)

Полученная система есть система алгебраических уравнений относительно неизвестных . Метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5.

ПРИМЕР. Приближение функции по методу наименьших квадратов.

Достаточно часто степень аппроксимационного многочлена известна.

Получим значения коэффициентов в простейших случаях



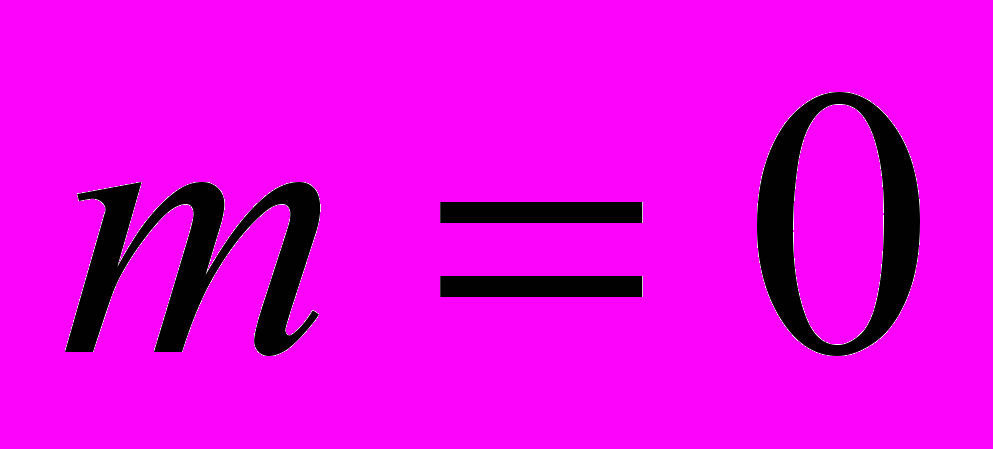
Система уравнений (4) принимает следующий вид:

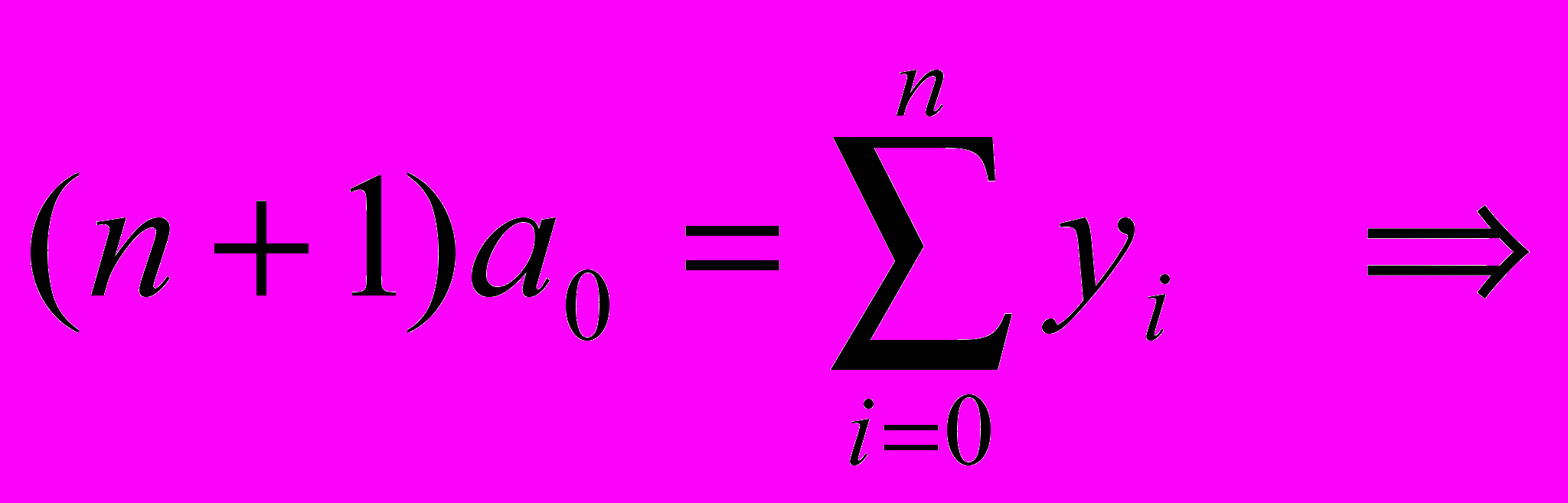
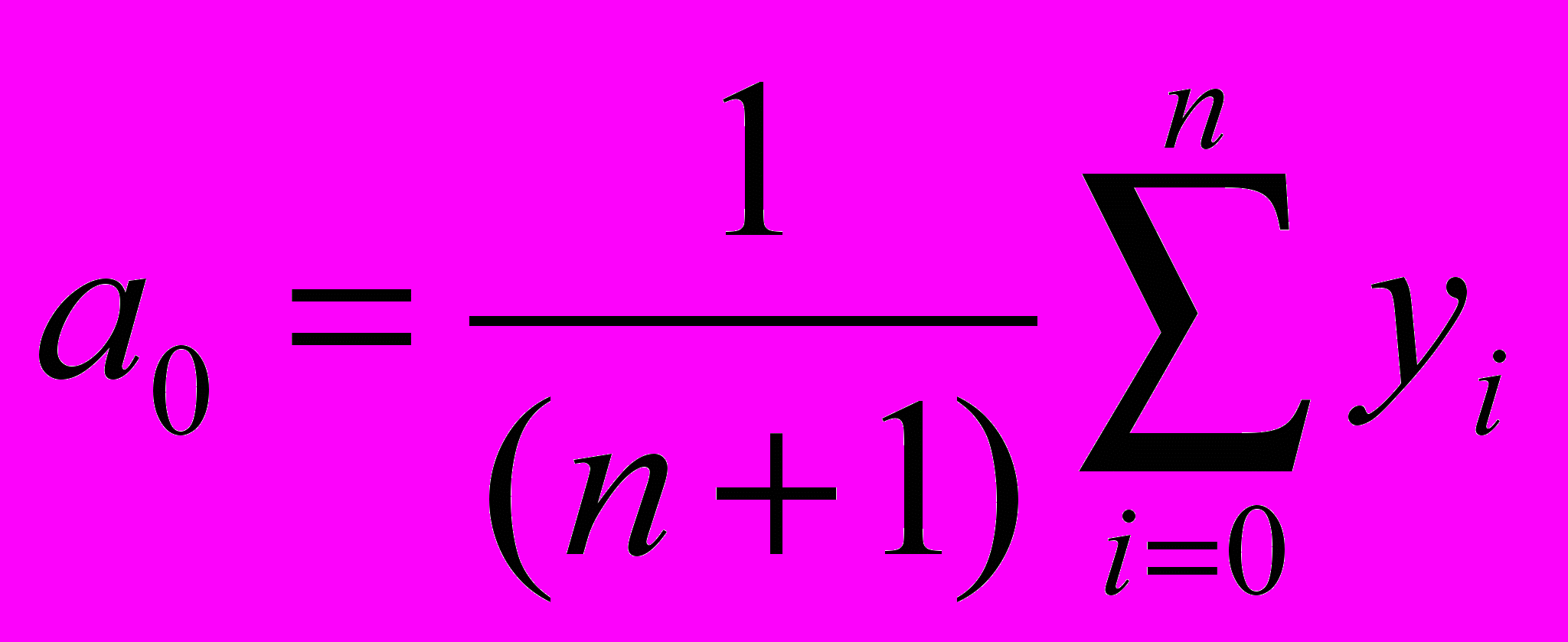(5)



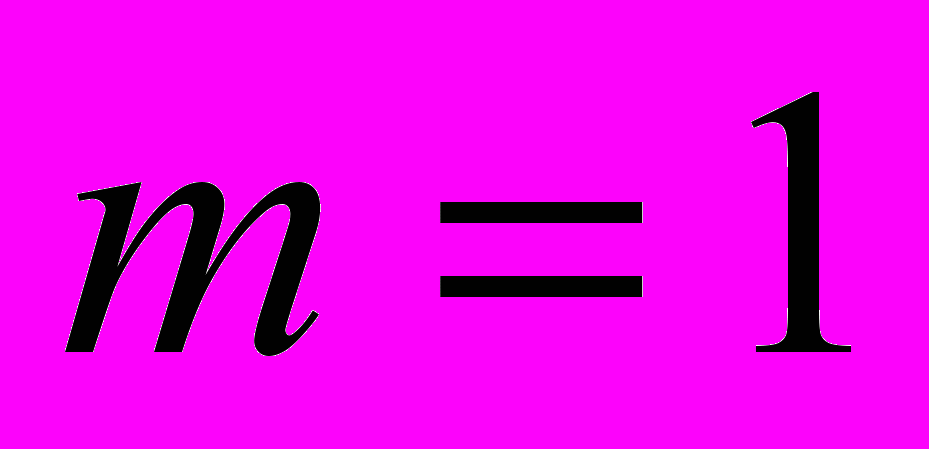
Система уравнений (4) принимает следующий вид:

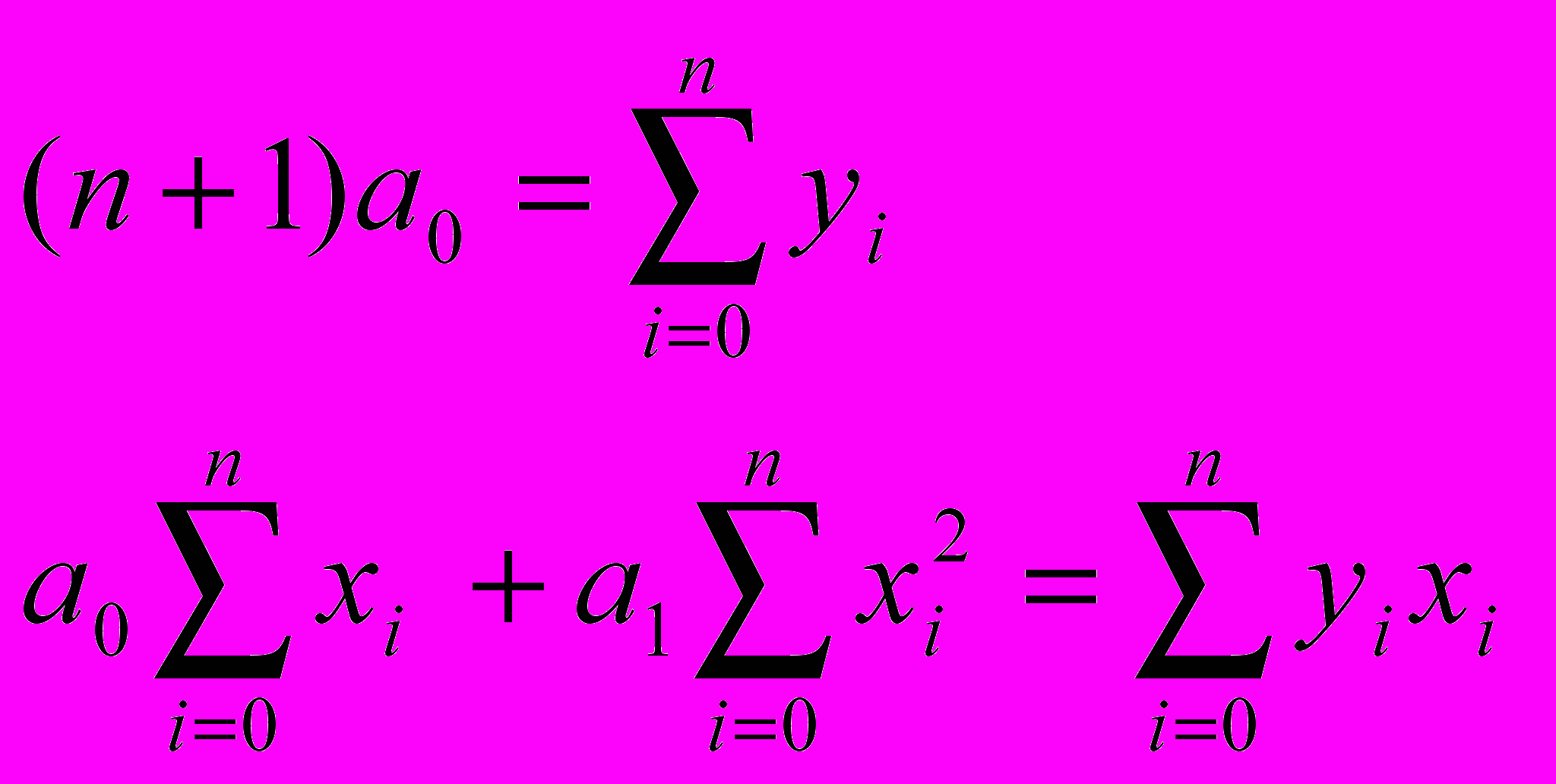(6)

Откуда можно получить следующие выражения на коэффициенты

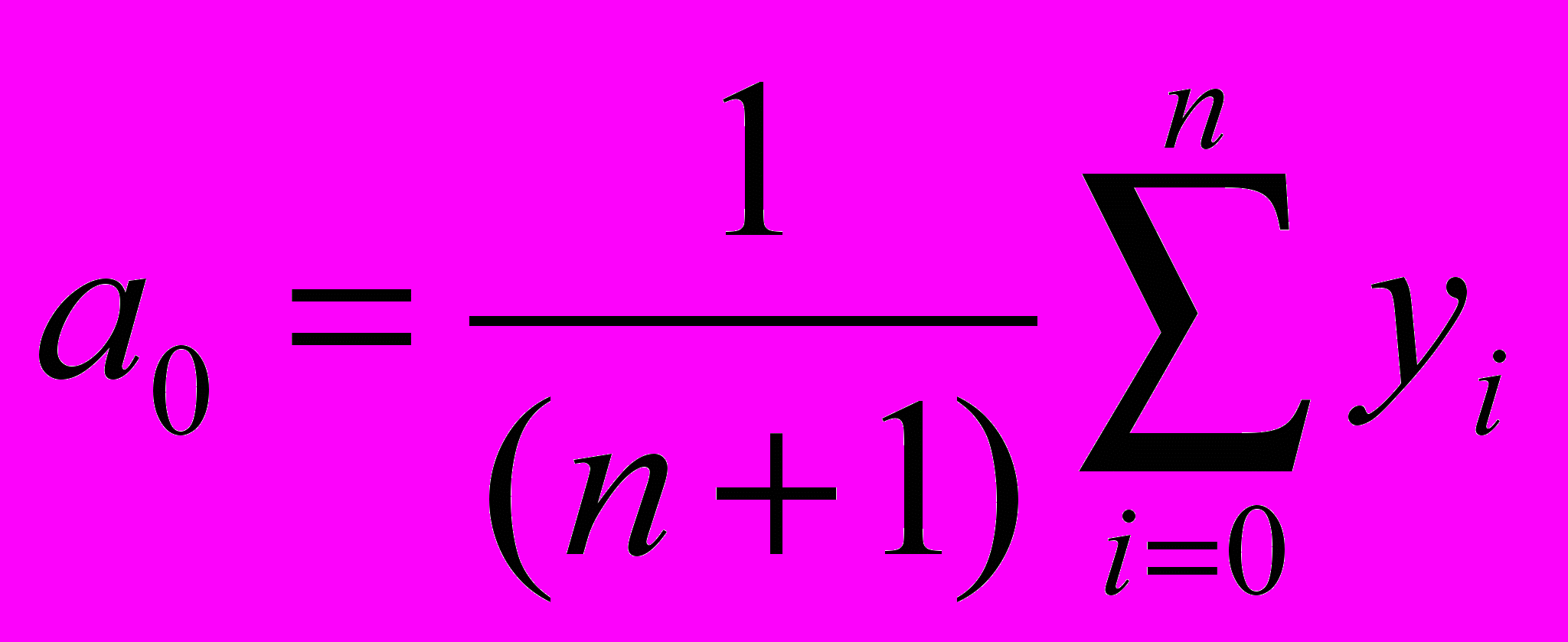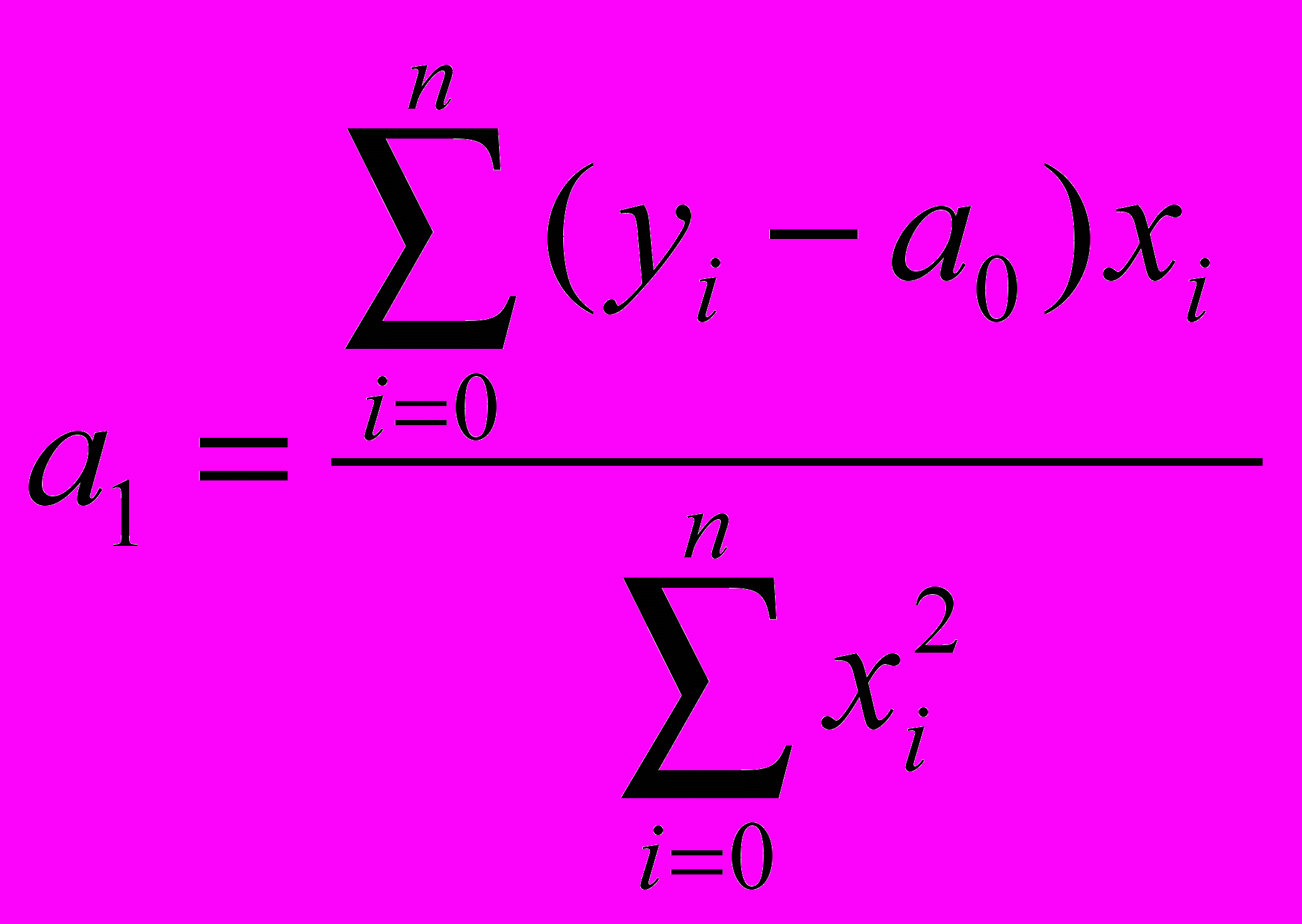, (7)

Расчет случайной погрешности средствами Excel

С использованием встроенных функций Excel расчет доверительного интервала проводится следующим образом.

1) Рассчитывается среднее значение

=СРЗНАЧ(число1; число2; ...)
число1, число2, ...  — аргументы, для которых вычисляется среднее.

2) Рассчитывается стандартное отклонение

=СТАНДОТКЛОНП(число1; число2; ...)
число1, число2, ...  — аргументы, для которых вычисляется стандартное отклонение.

3) Рассчитывается абсолютная погрешность

=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа  — уровень значимости используемый для вычисления уровня надежности.

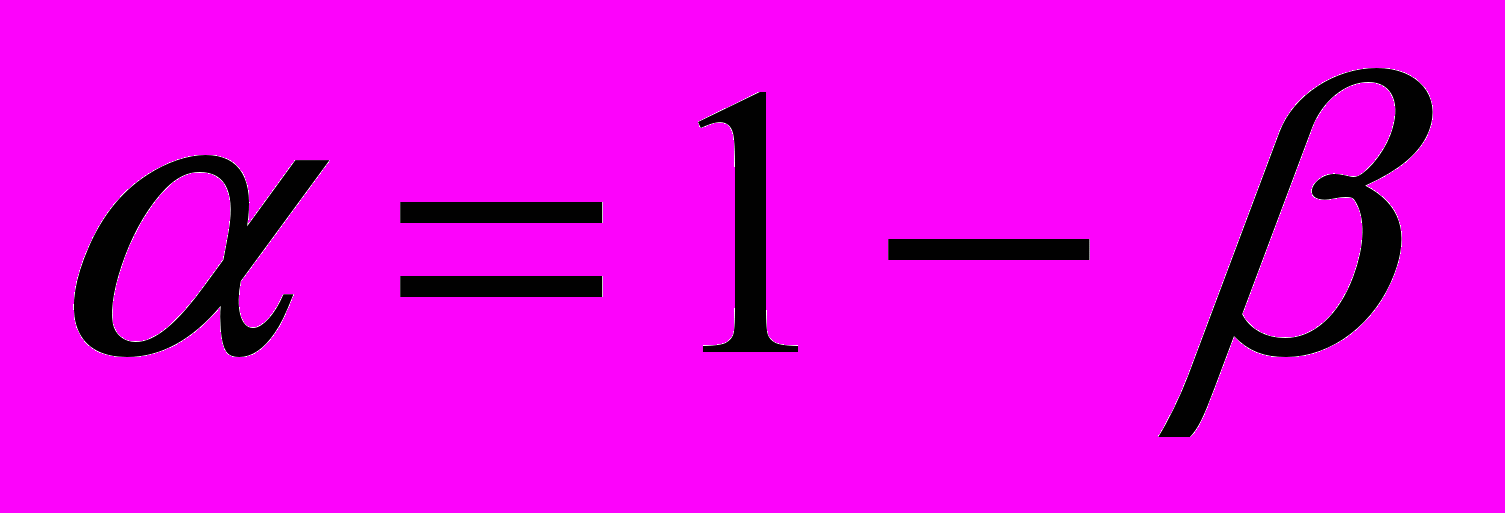(, т.е. 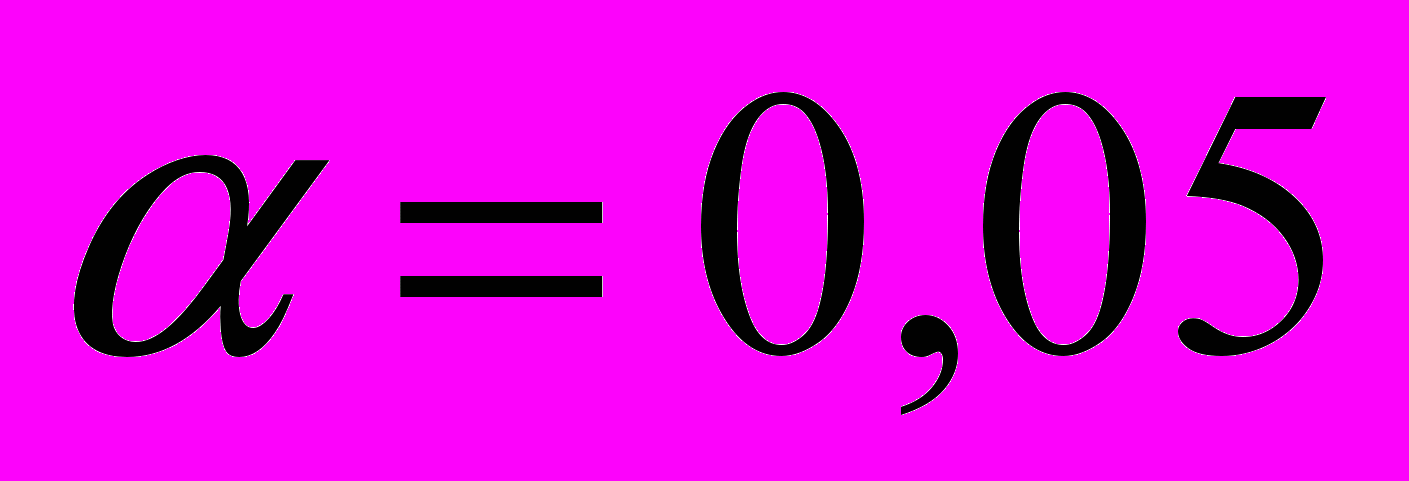означает надежности);
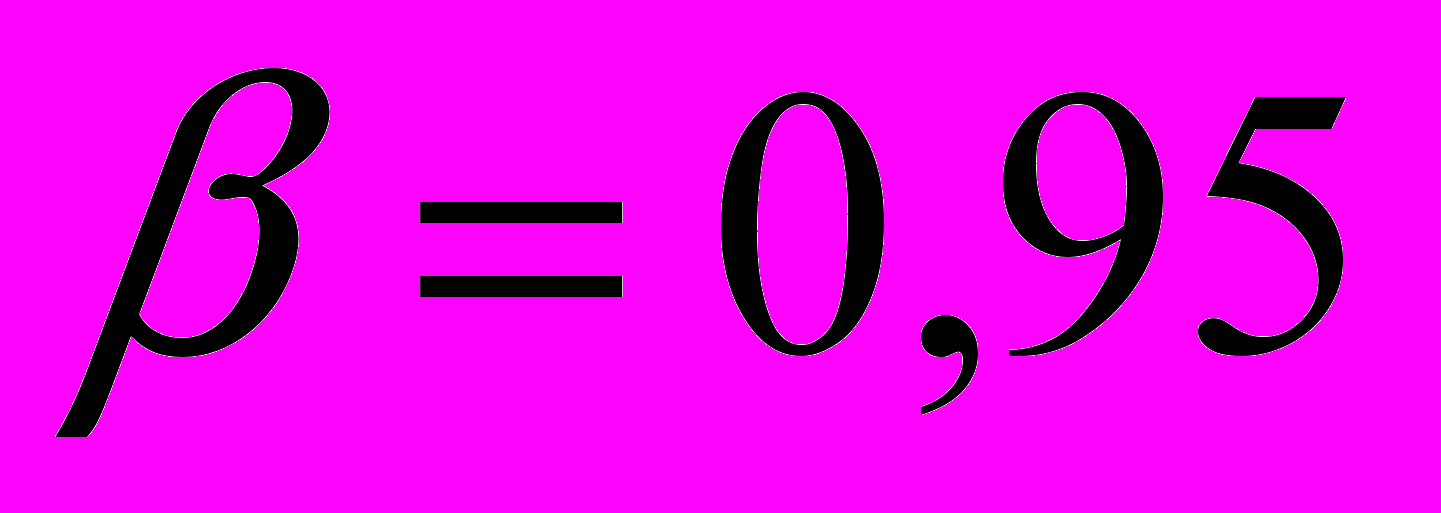станд_откл  — стандартное отклонение, предполагается известным;
размер  — размер выборки.

Лабораторная работа 1: Компьютерная обработка экспериментальных данных (2 часа).

Задание: Обработать заданный набор экспериментальных данных методом Стьюдента, построить экспериментальные кривые методом наименьших квадратов.

Предположим, в ходе эксперимента по измерению электросопротивления были получены следующие данные:



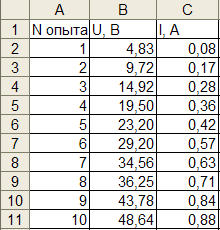
Используя для определения сопротивления закон Ома 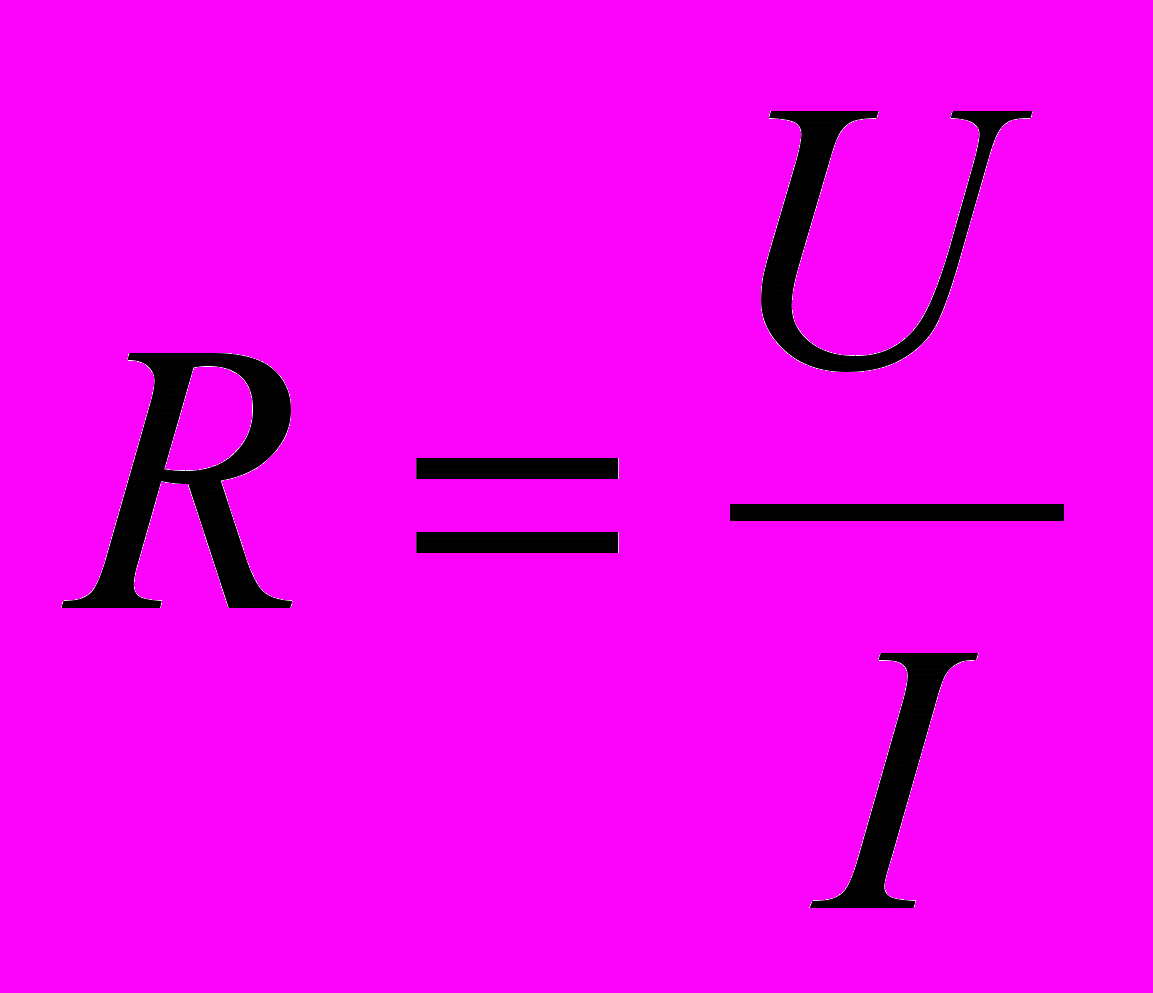произведем обработку данной серии экспериментальных данных.

Используемуе формулы

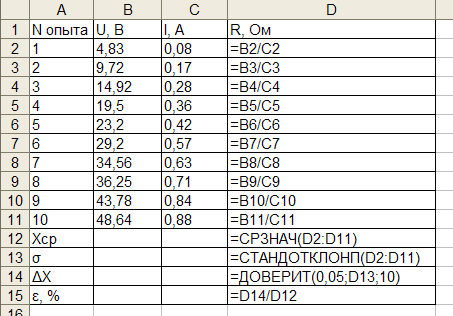Результат расчета

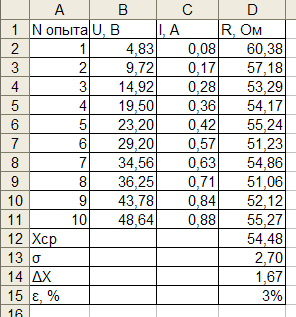Для построения графика используем мастер диаграмм.

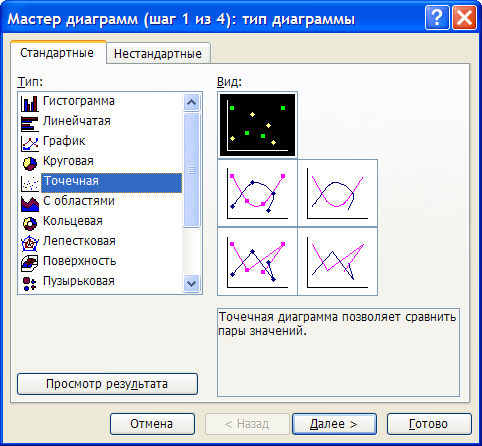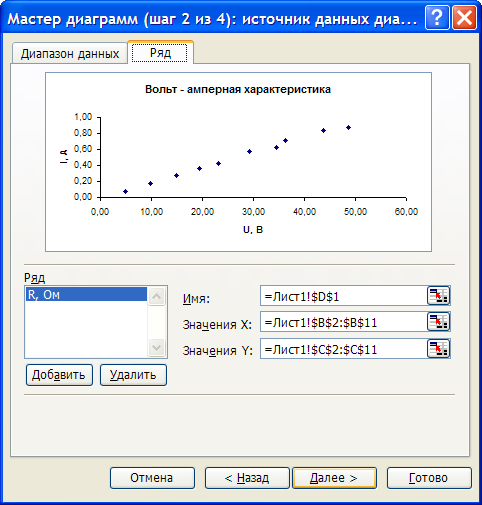Полученные экспериментальные данные следует аппроксимировать. Для выполнения этой процедуры в Excel предусмотрен мастер, добавляющий линию тренда, производящий аппроксимацию и сглаживание.

В меню «Диаграмма» выберите пункт «Добавить линию тренда…».




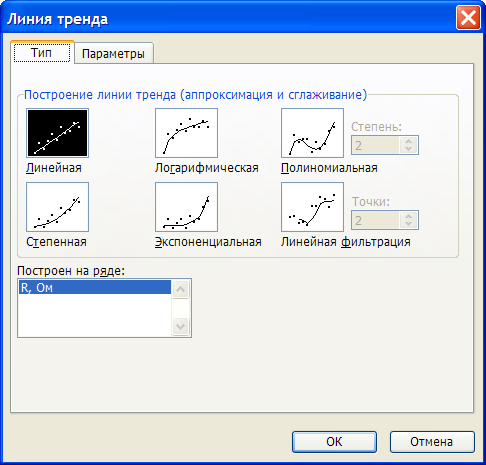
В результате, должен получиться следующий график.

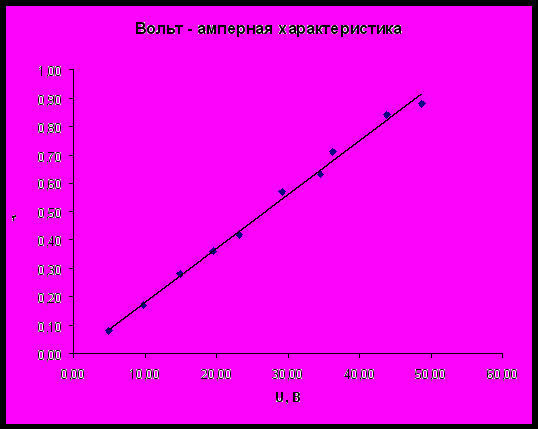
§2. Вычисление определенных интегралов.

Для вычисления определенных интегралов можно использовать различные численные методы (например, метод прямоугольников, трапеций, Симпсона).

Так в методе трапеций область интегрирования разбивается на отрезки с некоторым шагом и площадь под графиком функции на каждом отрезке считается равной площади трапеции.



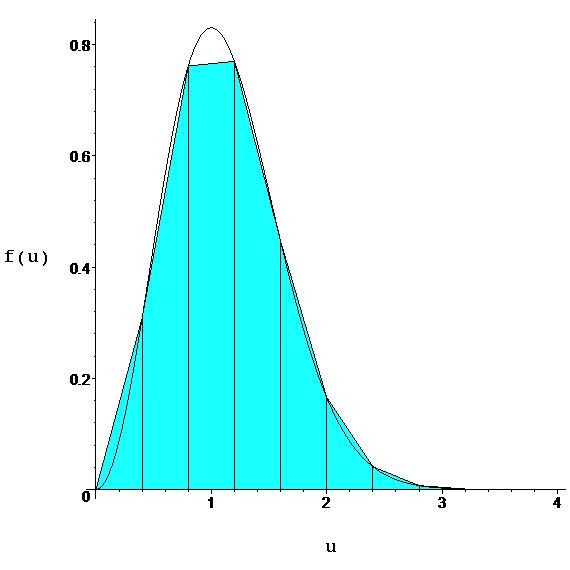
Таким образом при использовании метода трапеций расчетная формула принимает следующий вид:

,
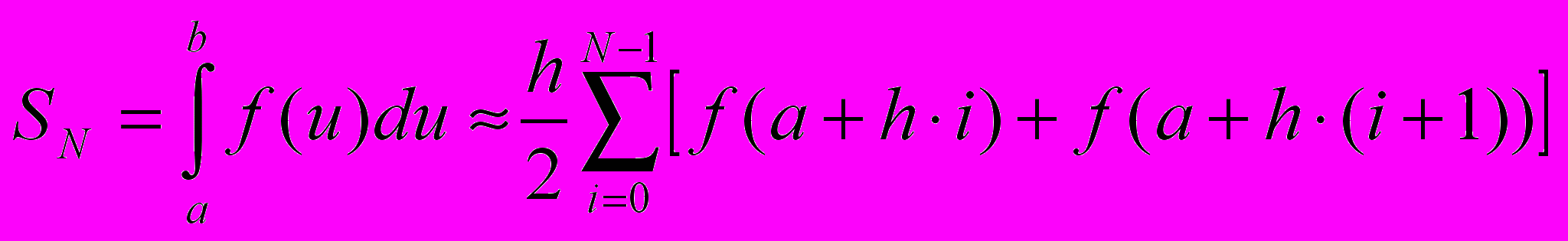где h=(b-a)/N шаг разбиения, N количество точек разбиения.

Для контроля точности количество точек разбиения удваивается, повторно выполняется расчет интеграла. Дробление исходного интервала прекращают когда достигнута требуемая точность:



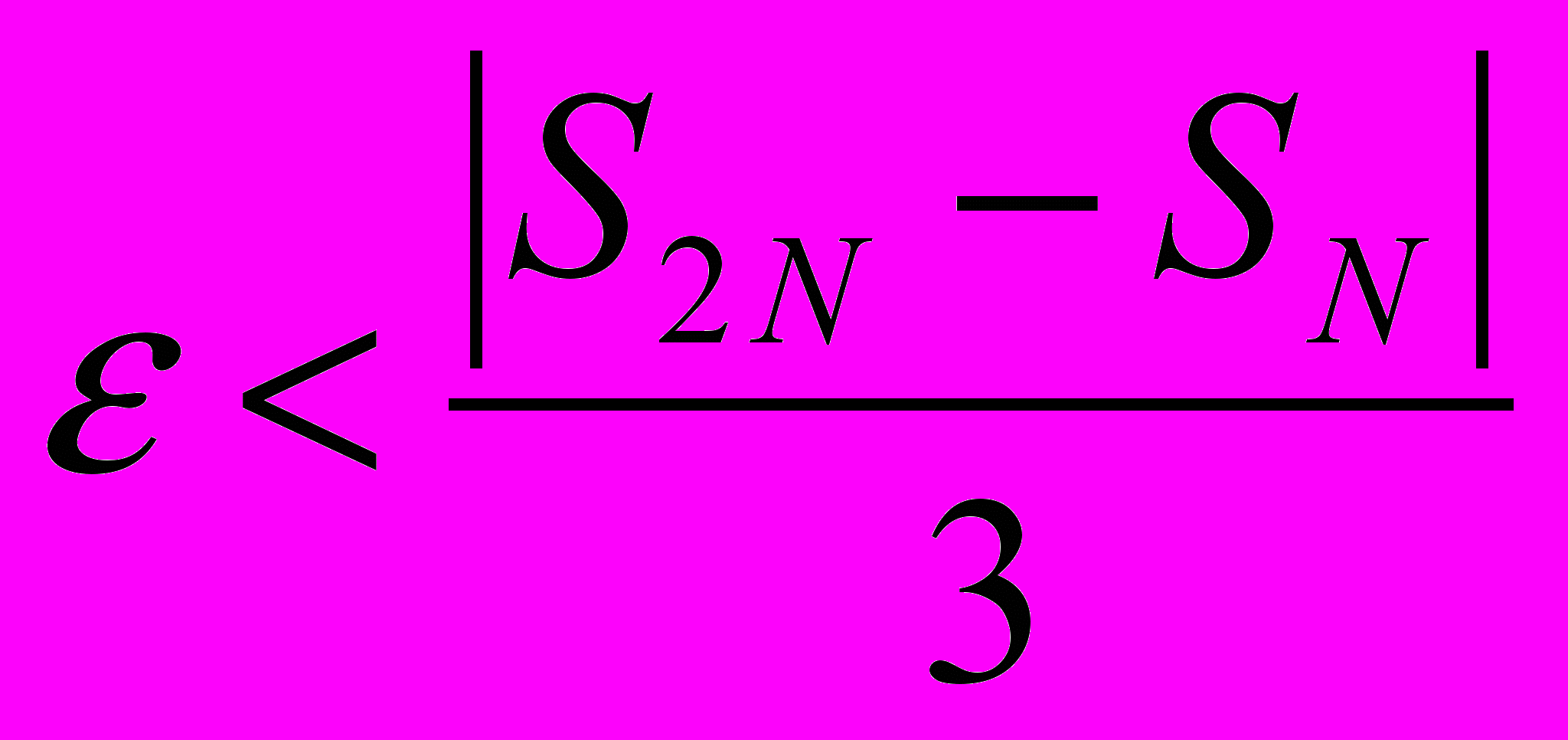
Для уменьшения времени, затрачиваемого на вычисления в алгоритме при получении S_2n  используется формула:



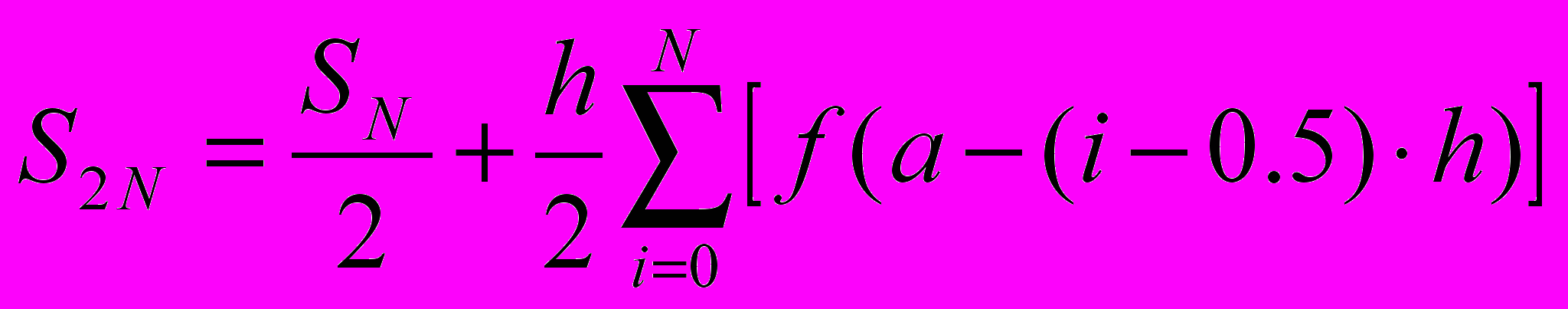
При выполнении работы можно использовать процедуры, приведенные в приложении.

Лабораторная работа 2: Распределение Максвелла.

Задание: Вычислить определенные интегралы при помощи формул трапеций, Симпсона.

Функция распределения Максвелла

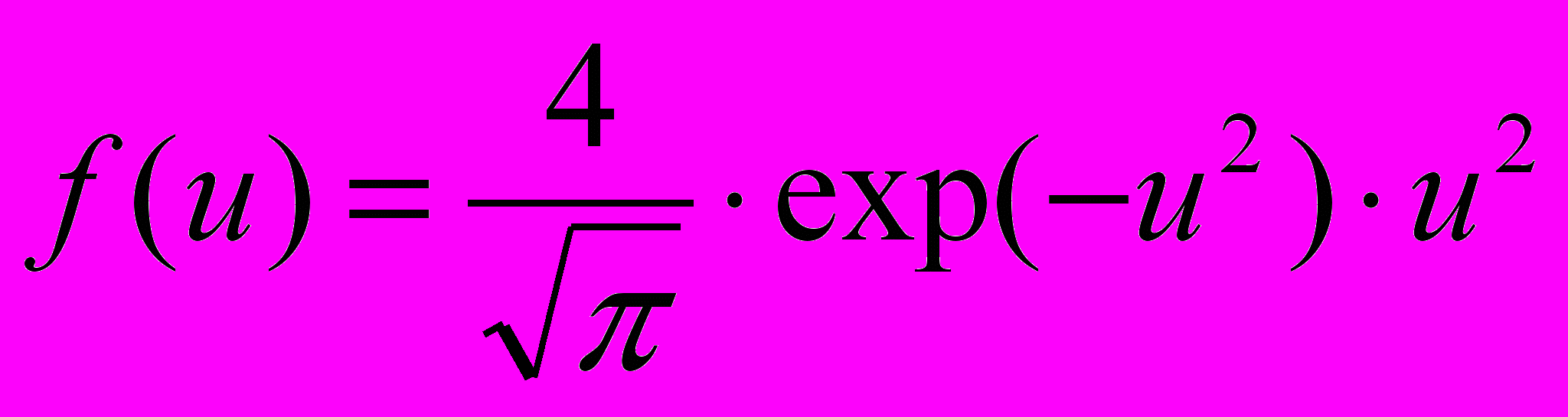, (1)
позволяет определить вероятность молекуле идеального газа иметь скорость 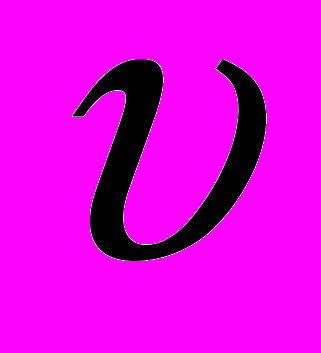в некотором интервале скоростей, где ­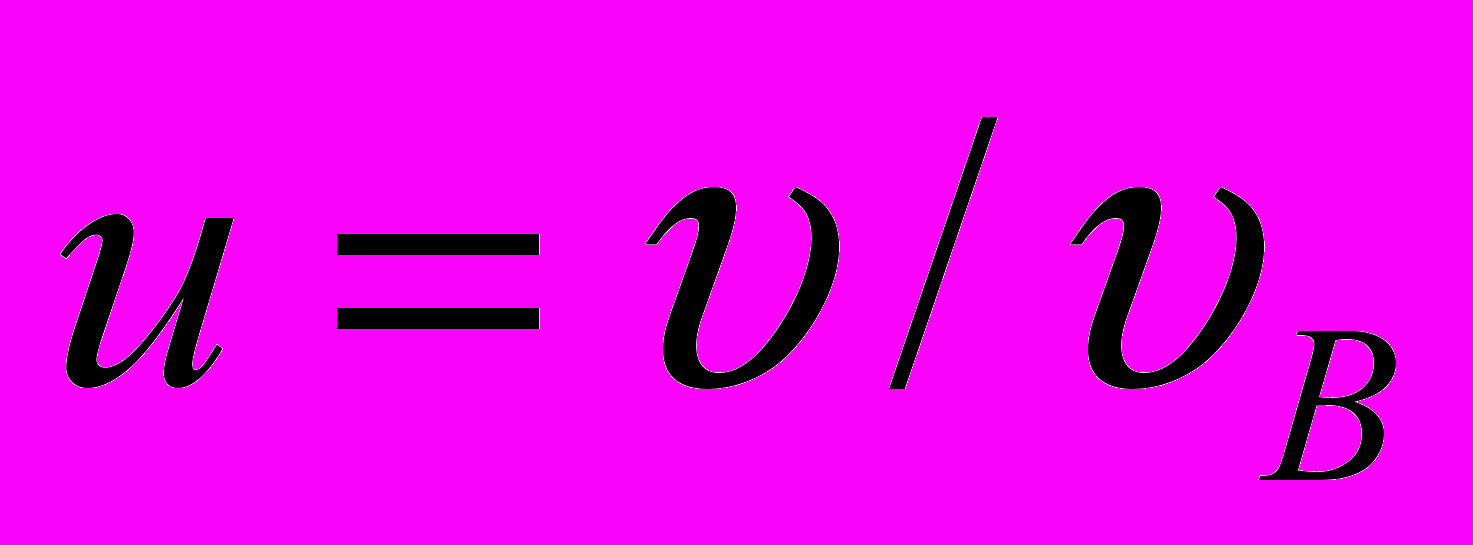 относительная скорость, ­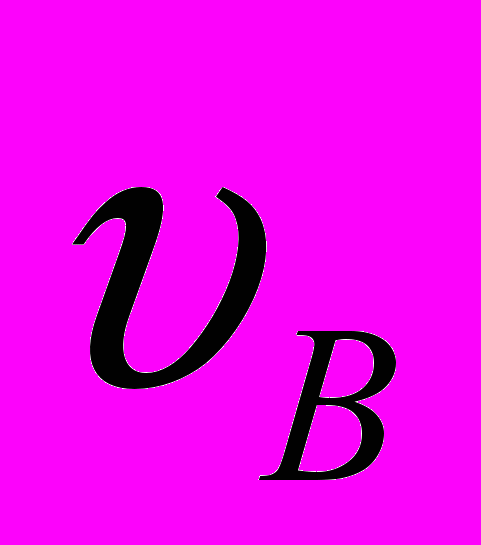 наиболее вероятная скорость.

При этом доля молекул идеального газа с относительными скоростями в интервале от 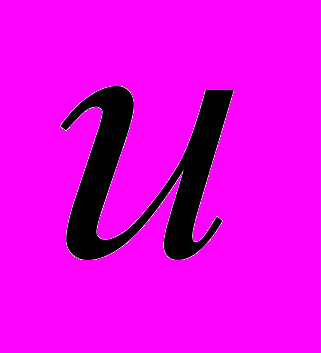до 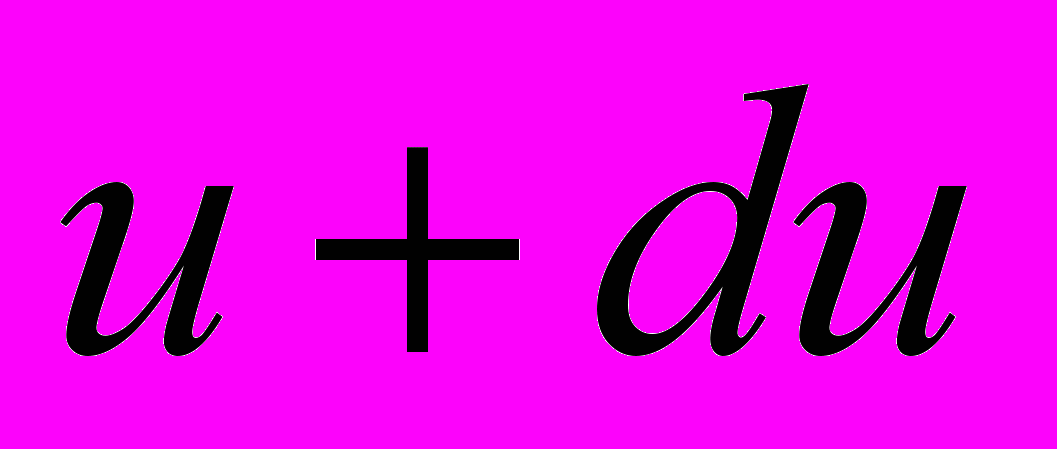определяется интегралом:

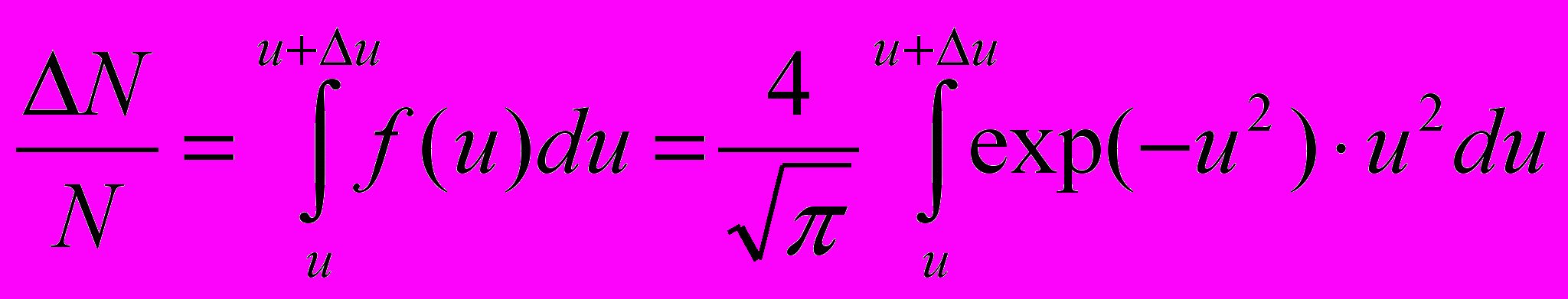(2)

Так как молекула всегда будет обладать некоторой скоростью, то количество молекул со скоростями в интервале 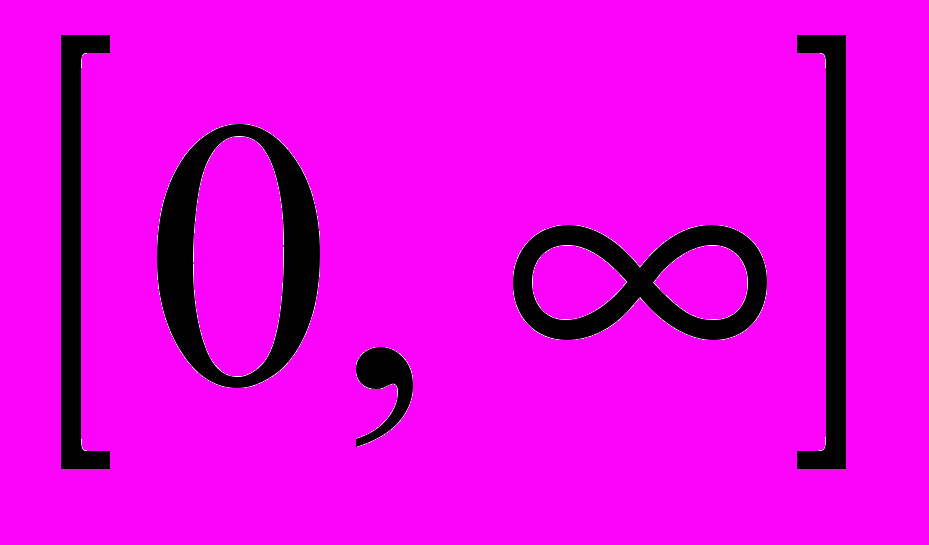будет равно полному числу молекул, то есть:

.

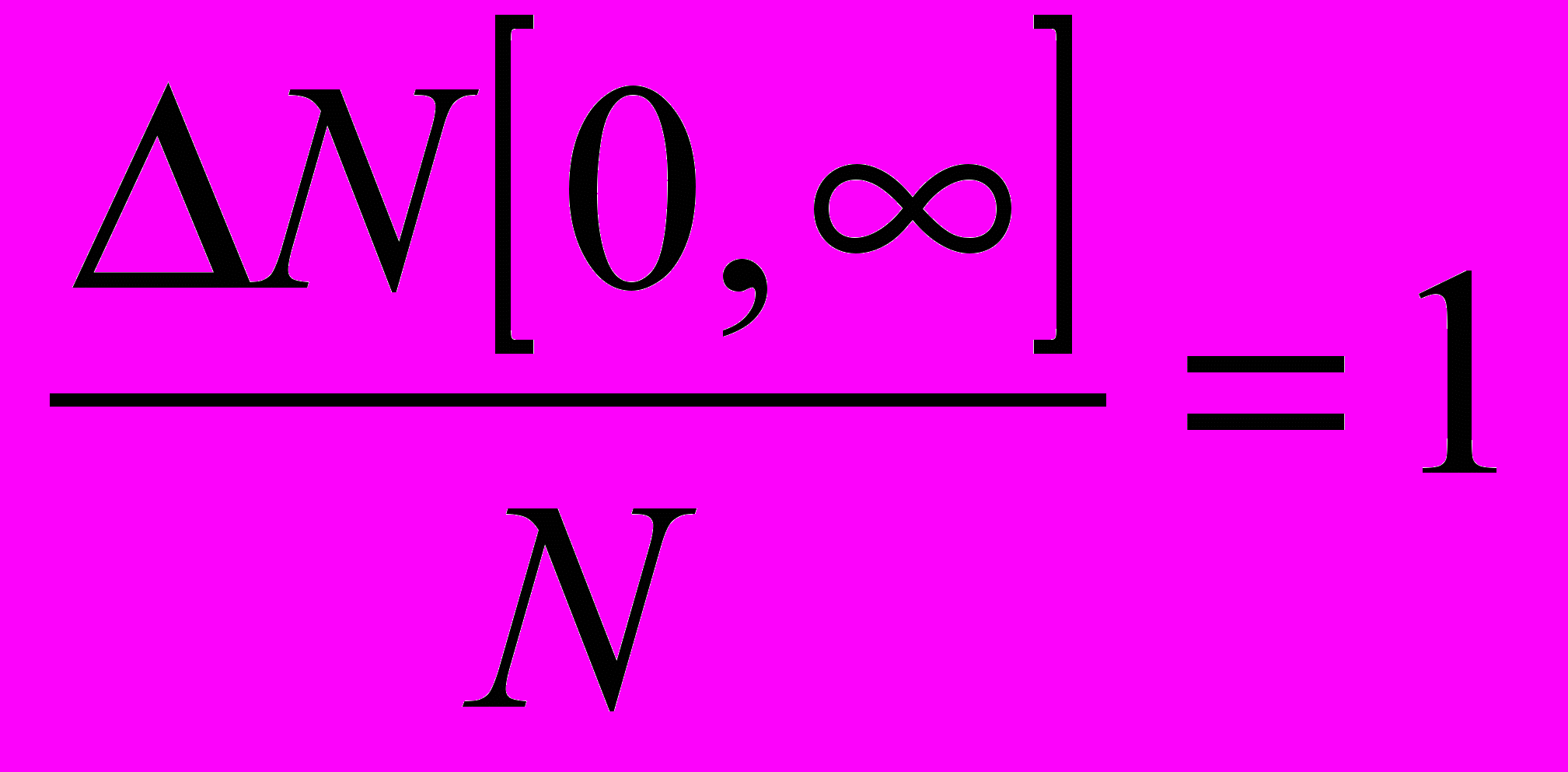Поэтому должно выполняться условие нормировки функции Максвелла:

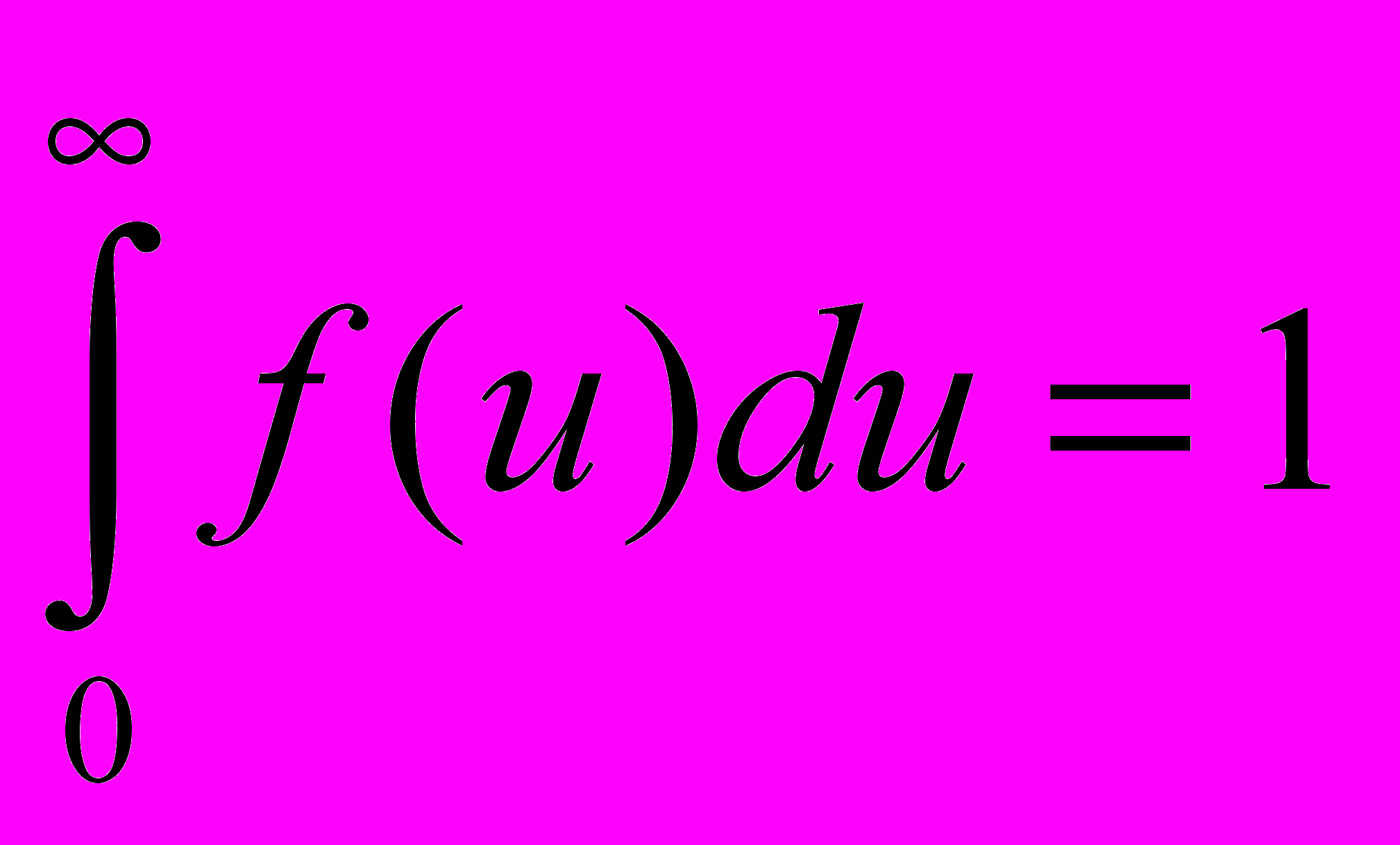. (3)

Ход работы

1) Проверить соотношение 1

Лабораторная работа 3

Тема:

Задание: Рассчитать координаты центра масс различных тел, вычислить моменты инерции тел.

Приложение к лабораторным работам 2,3.

Расчет определенного интеграла методом трапеций

/***********************************************************************

This code is generated by the AlgoPascal translator

This code is distributed under the ALGLIB license

(see b.net/copyrules.php for details)

***********************************************************************/


#include "ap.h"


/*-----------------------------------------------

This routines must be defined by the programmer:


double f(double x);

-----------------------------------------------*/


double integraltrap(const double& a, const double& b, const double& epsilon);


/*************************************************************************

Интегрирование методом трапеций с оценкой точности.


Считается интеграл функции F на отрезке [a,b] с погрешностью

порядка Epsilon.


function IntegralTrap(a:Real;b:Real;Epsilon:real):real;

*************************************************************************/

double integraltrap(const double& a, const double& b, const double& epsilon)

{

double result;

int i;

int n;

double h;

double s1;

double s2;


n = 1;

h = b-a;

s2 = h*(f(a)+f(b))/2;

do

{

s1 = s2;

s2 = 0;

i = 1;

do

{

s2 = s2+f(a-h/2+h*i);

i = i+1;

}

while(i<=n);

s2 = s1/2+s2*h/2;

n = 2*n;

h = h/2;

}

while(fabs(s2-s1)>3*epsilon);

result = s2;

return result;

}

Оглавление

Литература

1. Х. Гулд, Я. Тобочник.Компьютерное моделирование в физике. ч.1, 2.
   
2. Дж. Форсайт и др. Машинные методы математических вычислений. М.: Мир, 1980
   
3. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. М.: 1990.
   
4. Самарский А.А., Гулин А.В. Численные методы. М.: 1989.
   
5. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений / Пер. с англ. под ред. А.А. Абрамова. М.: 1986.
   
6. Березин И.С., Жидков Н.П. Методы вычислений. В 2-х томах. М.: 1966.