Учебно-методический комплекс по дисциплине Физика Конденсированного Состояния Для специальности 010701 Физика

Вид материала

Содержание

Требования Государственного Образовательного Стандарта по дисциплине «Теория Функций Комплексного Переменного».
Примерная программа курса, рекомендуемая УМО «Физика»
Упругие свойства кристаллов. Анализ упругих деформаций и напряжений. Модули упругости и уругие постоянные. Упругие волны в кубич
Кинетические явления в полупроводниках.
Генерация и рекомбинация неравновесных носителей заряда
Диффузия и дрейф неравновесных носителей заряда в полупроводниках
Оптические свойства полупроводников.
Магнитные свойства твердых тел.
по курсу «Физика Конденсированного Состояния»
Рабочая программа составлена на основании примерной программы Томского государственного университета, «УМО Физика»
Золотарев М.Л./
Тематический план
Название и содержание разделов, тем, модулей
Аудиторная работа
Содержание дисциплины
Список учебной литературы
Электронный вариант в библиотеке факультета
2. Вопросы к экзамену (и зачету).
Сведения о переутверждении РП на текущий учебный год и регистрация изменений
Содержание изменений
...
Полное содержание

Подобный материал:

ГОУ ВПО «Кемеровский государственный университет»

Кафедра теоретической физики

Учебно-методический комплекс по дисциплине

Физика Конденсированного Состояния

Для специальности 010701 Физика

Кемерово 2007

СОДЕРЖАНИЕ

Требования государственного образовательного стандарта высшего профессионального образования (Специальность 010701 – физика) к обязательному минимуму содержания основной образовательной программы и к уровню подготовки выпускника по курсу «Физика Конденсированного Состояния».
Примерная учебная программа курса, рекомендуемая УМО «Физика»
Рабочая программа курса
Методические рекомендации по изучению дисциплины для студентов
Учебно-методические материалы
Оценочные и диагностические средства итоговой государственной аттестации и учебно-методическое обеспечение их проведения.
Электронный вариант всех документов.

Требования Государственного Образовательного Стандарта по дисциплине «Теория Функций Комплексного Переменного».

Согласно ГОС содержание курса должно отражать следующие основные положения дисциплины : адиабатический принцип Борна-Эренфеста. Состояния электронов в кристаллической решетке. Зоны Бриллюэна, энергетические зоны. Примеси, примесные уровни. Дефекты. Статистика носителей заряда. Неравновесные электроны и дырки. Рассеяние носителей заряда, проводимость и кинетические свойства диэлектриков, металлов и полупроводников. Квазичастицы. Акустические и оптические фононы, плазмоны, экситоны Френкеля и Ваннье. Конденсация бозонов. Сверхтекучесть. Электрон-фононные взаимодействия. Полярон Фрелиха. Взаимодействие света с кристаллической решеткой, поляритоны. Оптические свойства диэлектриков, металлов и полупроводников. Поверхностные состояния электронов. Состояния электронов в структурах с пониженной размерностью.

Примерная программа курса, рекомендуемая УМО «Физика»^¹

(ссылка скрыта)

Введение Краткий исторический обзор развития физики полупроводников, значение полупроводниковых материалов в современной науке и технике. Предмет и содержание курса.

Упругие свойства кристаллов. Анализ упругих деформаций и напряжений. Модули упругости и уругие постоянные. Упругие волны в кубических кристаллах.

Тепловые колебания атомов кристаллической решетки. Колебания и волны в простой и сложной одномерных решетках. Колебания и волны в трехмерной кристаллической решетке. Квантование колебаний кристаллической решетки. Фононы.

Основы зонной теории твердого тела.Уравнение Шредингера для кристалла, одноэлектронное приближение. Зоны разрешенных значений энергии электрона в кристалле. Зоны Бриллюэна. Движение носителей заряда в кристалле под действием электрического поля, понятие эффективной массы, тензор обратной эффективной массы. Элементарная теория примесных состояний. Зонная структура некоторых полупроводников (германий, кремний, арсенид галлия).

Статистика электронов и дырок в твердом теле. Функция распределения в статистике Ферми-Дирака. Плотность квантовых состояний. Концентрация электронов и дырок. Положение уровня Ферми и концентрация носителей заряда в собственном полупроводнике. Концентрация легких и тяжелых дырок в полупроводниках с вырожденными зонами (германий, кремний). Уравнение электронейтральности. Функция распределения носителей заряда по примесным состояниям. Температурная зависимость уровня Ферми и концентрации носителей заряда в полупроводнике, легированном одним типом примеси, и в компенсированном полупроводнике. Вырожденные и частично вырожденные полупроводники.

Кинетические явления в полупроводниках. Кинетическое уравнение Больцмана, приближение времени релаксации. Функция распределения электронов по энергиям в полупроводнике со стандартной зоной. Электропроводность невырожденного и вырожденного полупроводников со стандартной зоной. Проводимость многодолинного полупроводника. Температурная зависимость подвижности и электрической проводимости при различных механизмах рассеяния носителей заряда. Эффект Холла в полупроводниках со смешанной проводимостью. Магниторезистивный эффект. Термоэлектрические явления (термоэдс, эффекты Пельтье и Томсона)

Генерация и рекомбинация неравновесных носителей заряда. Равновесные и неравновесные носители заряда, квазиуровни Ферми. Скорость изменения концентрации носителей заряда в полупроводнике при биполярной генерации и межзонной рекомбинации. Изменение концентрации избыточных носителей заряда при включении и выключении внешнего ионизатора при низком и высоком уровне возбуждения, время жизни носителей заряда. Монополярная генерация, время релаксации Максвелла. Различные механизмы рекомбинации носителей заряда (излучательная, безизлучательная, ударная, плазменная и экситонная). Рекомбинация через рекомбинационные центры, зависимость времени жизни от положения уровня Ферми в полупроводнике и от температуры. Поверхностная рекомбинация, понятие о скорости поверхностной рекомбинации.

Диффузия и дрейф неравновесных носителей заряда в полупроводниках. Уравнение непрерывности. Соотношения Эйнштейна. Диффузия и дрейф неравновесных основных носителей заряда, длина экранирования. Диффузия и дрейф избыточных неосновных носителей заряда в примесном полупроводнике, длина затягивания и диффузионная длина. Диффузия и дрейф неравновесных носителей заряда в полупроводнике, близком к собственному, коэффициент биполярной диффузии, биполярная дрейфовая подвижность.

Оптические свойства полупроводников. Спектр отражения и спектр поглощения оптического излучения. Собственное поглощение света, прямые и непрямые переходы. Экситонное поглощение, поглощение свободными носителями заряда, примесное и решеточное поглощение. Фоторезистивный эффект, квантовый выход, коэффициент усиления. Зависимость фототока от интенсивности света, кинетика фототока.

Магнитные свойства твердых тел. Магнитные свойства атомов. Классификация твердых тел по магнитным свойствам.Диамагнетизм. Классическая теория диамагнетизма. Циклотронный резонанс, его практическое применение. Парамагнетизм. Классическая и квантовая теории парамагнетизма, электронный и ядерный парамагнитный резонанс, его практическое применение. Ферромагнетизм. Роль обменного взаимодействия в возникновении ферромагнетизма. Доменная структура ферромагнитных тел. Антиферромагнетизм. Ферримагнетизм. Магнитные спектры вещества.

Федеральное агентство по образованию

ГОУ ВПО «Кемеровский государственный университет»

Кафедра теоретической физики

«Утверждаю»

Декан физического факультета

______________________

(подпись)

«____» ______________ 200_ г.

РАБОЧАЯ ПРОГРАММА

по курсу «Физика Конденсированного Состояния»

для специальности 010701 ФИЗИКА, ОПД._____

(шифр и наименование специальности, цикл и компонент ГОС ВПО)

факультет Физический

курс _________4__________ экзамен ____8_____

семестр ______8__________ (семестр)

лекции ______34__________ (часов) зачет ____________

практические занятия _108_ (часов) (семестр)

лабораторные ____________(часов)

самостоятельные занятия _42_(часов)

Всего часов ________184__________

Составитель:

д.ф.-м.н., профессор кафедры теоретической физики КемГУ, А.Б.Гордиенко

Кемерово, 2007

Рабочая программа составлена на основании примерной программы Томского государственного университета, «УМО Физика»

Рабочая программа обсуждена на заседании кафедры

Протокол № ___ от «___» ________ 200__ г.

Зав. кафедрой _________________/ ____________./

(подпись, Ф.И.О.)

Одобрено методической комиссией

Протокол № ___ от «___» ________ 200 __ г.

Председатель___________________/ Золотарев М.Л./

(подпись, Ф.И.О.)

Пояснительная записка

Курс «Физика Конденсированного Состояния» входит в состав общих естественнонаучных дисциплин, изучаемых на физическом факультете Кемеровского Государственного Университета.

Цель курса «Физика Конденсированного Состояния» состоит в систематическом изложении способов и методов применения основных принципов квантовой теории к исследованию свойств кристаллических твердых тел.

Основные навыки, которыми должен обладать студент: знать основные свойства протяженных систем, обусловленные квантовым характером взаимодействий, обладать навыками работы с объектами, которые характерны для рассматриваемых систем, включая прямое и обратное пространство, операции симметрии, многоэлектронные волновые функции, иметь представление о методах решения многоэлектронных задач, таких, как метод Хартри, Хартри-Фока, Теория Функционала Плотности, а также специальных методах решения задачи о расчете электронной структуры кристаллов, включая, в том числе, и их приближенные варианты – метод сильной связи, метод почти свободных электронов, метод эффективной массы. Указанные навыки должны служить основой для понимания физических основ таких явлений, как электрон-фононное взаимодействие, сверхпроводимость, а также широкого спектра оптических процессов в конденсированном состоянии.

Тематический план

№	Название и содержание разделов, тем, модулей	Объем часов					Формы контроля
		Общий	Аудиторная работа			Самостоятельная работа
		Общий	Лекции	Практические (или семинарские)	Лабораторные	Самостоятельная работа
1	2	3	4	5	6	7	8
1	Введение. Основные понятия.		2	2
2	Основные положения физики твердого тела.		2	2
3	Квантовая задача многих тел.		2	2
4	Адиабатическое приближение.		2	2
5	Одноэлектронное приближение		2	2
6	Антисимметризованные волновые функции.		2	2
7	Теория Функционала Плотности		2	2
8	Метод Кона-Шэма.		2	2
9	Методы решения уравнений зонной теории.		2	2
10	Линейные методы.		2	2
11	Приближенные методы.		2	2
12	Электрон-фононное взаимодействие.
13	Электрон-фононное взаимодействие в ионных кристаллах.			2
14	Сверхпроводимость.		2	2
15	Сверхпроводимость: микроскопическая теория .		2	2
16	Оптические свойства кристаллов.
17	Квантовая теория оптических свойств кристаллов











Итого:			36

Содержание дисциплины

1. Содержание частей, разделов и тем курса

Тема	Содержание	Литература
1. Введение. Основные понятия.	Трансляционная симметрия, основные векторы трансляций, элементарная ячейка, ячейка Вигнера-Зейтца, обратная решетка, первая зона Бриллюэна, система единиц (атомная, релятивистская)	[1]-[6]
2. Основные положения физики твердого тела.	периодический потенциал, теорема Блоха, зонная структура, дисперсионная зависимость, классификация твердых тел. Элементарные возбуждения. Квазичастицы	[1]-[6]
3. Квантовая задача многих тел.	Общая формулировка квантовой задачи многих тел. Многоэлектронное уравнение Шредингера, Гамильтониан.	[1]-[6]
4. Адиабатическое приближение.	Разделение атомных и электронных координат.	[1]-[6]
5. Одноэлектронное приближение.	Валентное приближение. Вариационный принцип Ритца. Уравнения Хартри. Самосогласованный потенциал. Решение «самосогласованных» уравнений.	[1]-[6]
6. Антисимметризованные волновые функции.	Определитель Слэйтера. Вычисление средних значений с детерминантными функциями. Вариационный принцип. Уравнения Хартри-Фока. Обменная энергия.	[1]-[6]
7. Теория Функционала Плотности	Электронная плотность, определение, основные свойства. Первая теорема Хоэнберга-Кона. Вторая теорема Хоэнберга-Кона, вариационный принцип для электронной плотности. Функционал полной энергии.	[1]-[6]
8. Метод Кона-Шэма.	Построение функционала энергии с использованием фиктивной системы невзаимодействуюших частиц. Уравнения Кона-Шэма. Обменно-корреляционная энергия.	[1]-[6]

(продолжение)

9. Методы решения уравнений зонной теории	Общая формулировка задачи. Базисные функции. Секулярное уравнение. Метод плоских волн. Метод присоединенных плоских волн. Метод ортогонализованных плоских волн. Псевдопотенциал.	[1]-[6]
10. Линейные методы.	Линеаризация. Линейный метод присоединенных плоских волн (ЛППВ).	[1]-[6]
11. Приближенные методы.	Электрон в пустой решетке. Метод сильной связи. Метод почти свободных электронов. Эффективная масса. Теорема Ванье.	[1]-[6]
11. Электрон-фононное взаимодействие.	Общие свойства взаимодействия электрона с колебаниями решетки. Тензор деформации, локальность. Деформационный потенциал.	[1]-[6]
12. Электрон-фононное взаимодействие.	Гармонический осциллятор. Вторичное квантование, операторы рождения и уничтожения. Понятие полевых операторов. Гамильтониан для частиц с 2-х и 4-х частичным взаимодействиями. Гамильтониан невзаимодействующих фононов. Гамильтониан взаимодействия электронов с фононами в представлении чисел заполнения. Графическое представление, диаграммы Фейнмана. Простейшие типы взаимодействий. Виртуальные фононы.	[1]-[6]
13. Электрон-фононное взаимодействие в ионных кристаллах.	Взаимодействие электрона с деформацией решетки в случае вильной связи. Электрон-фононное взаимодействие в ионных кристаллах. Полярон. Модель Фрелиха.	[1]-[6]
14. Сверхпроводимость	Критическая температура. Эффект Мейснера-Оксенфельда. теория Лондонов. Уравнения Лондонов. Проникновение магнитного поля внутрь сверхпроводника. Теория Гинзбурга-Ландау. Параметр порядка. Уравнения Гинзбурга-Ландау. Длина когерентности. Сверхпроводники 1-го и 2-го рода. Квантование магнитного потока. Флюксон.	[1]-[6]
15. Сверхпроводимость: микроскопическая теория.	Электронное притяжение. Куперовские пары. Изотопический эффект.	[1]-[6]
16. Оптические свойства кристаллов	Виды взаимодействия света с твердым телом; оптические константы; поглощение света кристаллами, собственное поглощение; экситонное поглощение; поглощение свободными носителями; примесное поглощение; решеточное поглощение. Рекомбинационное излу-чение в полупроводниках. Межзонная рекомбинация. Рекомбинация через локализованные центры. Экситонная рекомбинация. Твердотельные лазеры.	[1]-[6]
17. Квантовая теория оптических свойств кристаллов	Общий теоретический анализ межзонных оптических переходов; дипольное приближение; вертикальные переходы; связь с оптическими константами. Оптические свойства кристалла кремния.	[1]-[6]

2. Содержание практических и семинарских занятий.

2.а. Перечень вопросов, выносимых на семинарские или практические занятия

Занятие 1. Структура и симметрия кристаллов. Решетка Бравэ. Основные векторы трансляций.

Занятие 2. Упаковка атомов в кристаллах. Коэффициент упаковки для решеток Бравэ. Атомные плоскости. Индексы Вейса.

Занятие 3. Обратная Решетка. Основные векторы трансляций обратной решетки. Зона Брилюэна.

Занятие 4. Общие свойства уравнения Шредингера для периодических систем. Теорема Блоха. Блоховские функции. kp-гамильтониан

Занятие 5. Модель Кронига-Пенни. Энергетические зоны.

Занятие 6. Метод плоских волн. Периодический потенциал. Зонная структура в методе плоских волн.

Занятие 7. Основные электронные характеристики: эффективная масса, скорость.

Занятие 8. Метод сильной связи. Функции Ваннье. Задачи на вычисление дисперсионной зависимости для простых структур.

2.б. Состав и содержание заданий, задач, которые предусмотрены для решения или разбора на занятиях.

Занятие 1.

Задача 1. Изобразить структуру кристалла, для которого векторы трансляции

и атомный базис

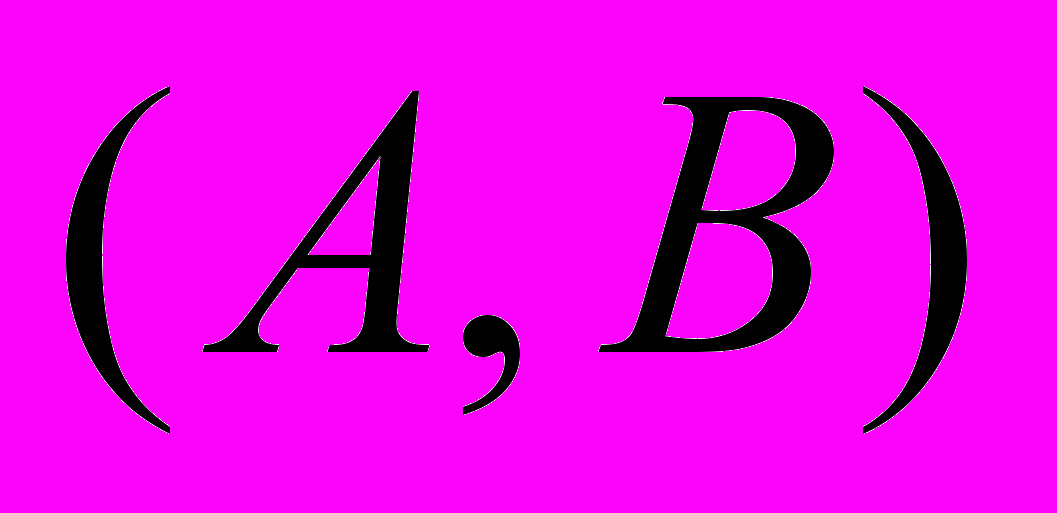определяются следующим образом:

а)

б)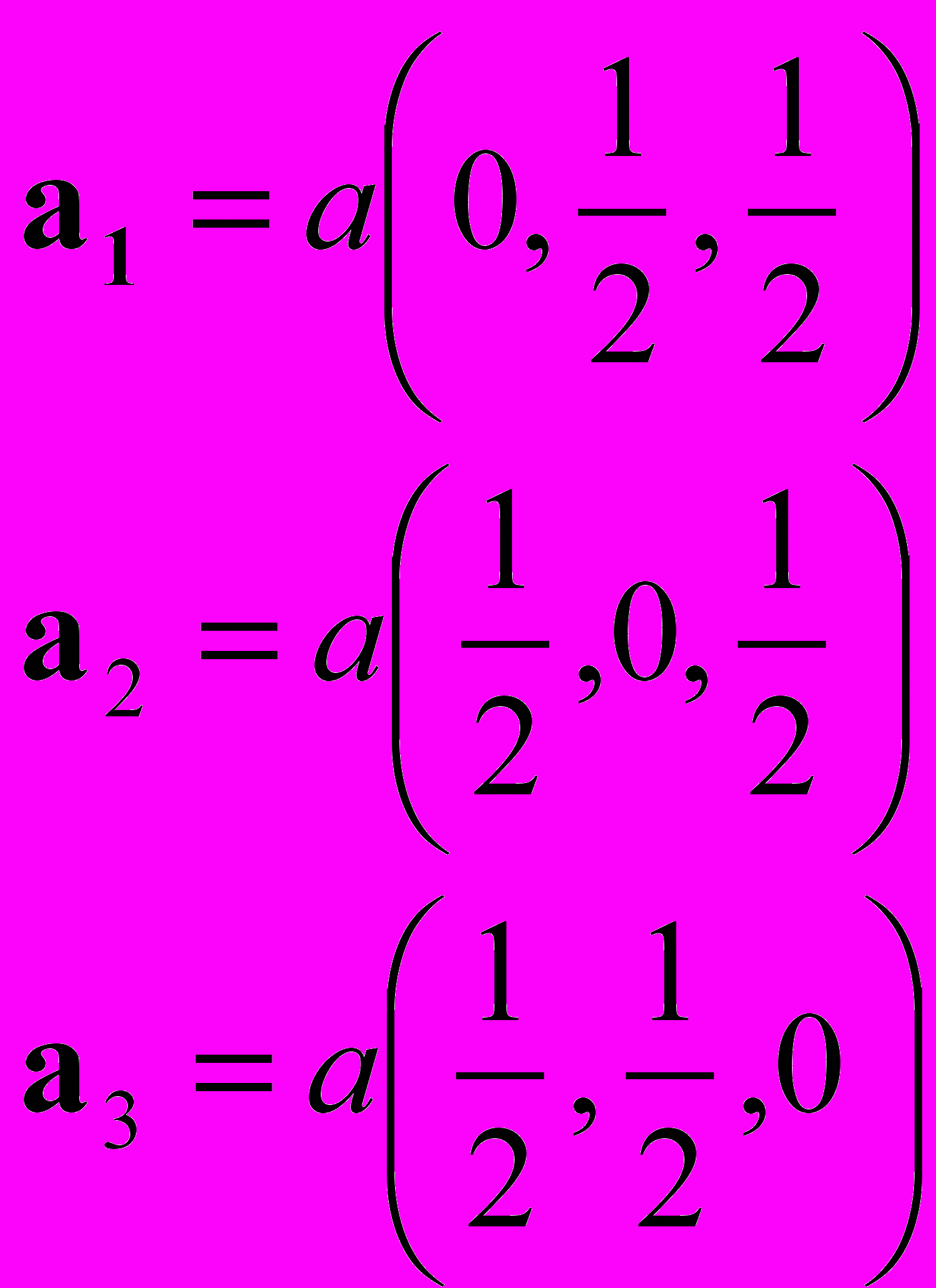

в)

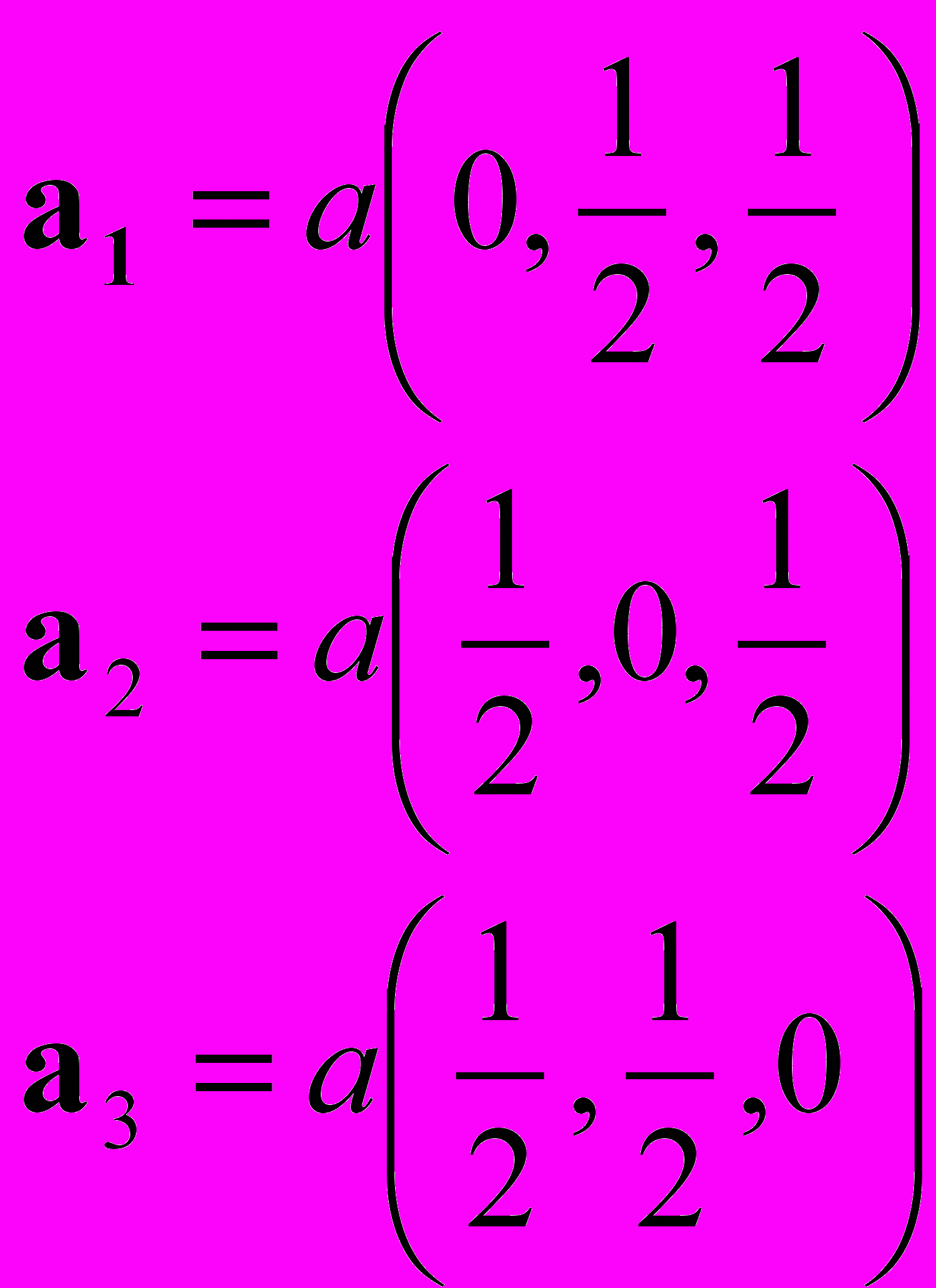
Задача 2. Определить число атомов в расширенной элементарной ячейке, типа NaCl, имеющей форму куба.

Задача 3. Пусть

- векторы трансляций некоторой решетки Бравэ. Определим три вектора

где

- целые числа. Показать, что если

,

где N – целое число, то векторы

образуют некоторый новый набор основных трансляций и найти объем элементарной ячейки, построенной на таких векторах.

Задача 4. Показать, что объемноцентрированная кубическая решетка может быть разделена на две простые кубические решетки А и В так, что ни одна пара ближайших соседей в исходной решетке не окажется в решетке А или В. Показать также, что простая кубическая решетка может рассматриваться как две гранецентрированные, а гранецентрированная как 4 простых.

Занятие 2.

Задача 1. Для структуры алмаза (сфалерита) найти величину тетраэдрического угла А-В-А.

Задача 2. Найти коэффициент упаковки для простой, объемноцентрированной и гранецентрированной кубической решетки.

Занятие 3.

Задача 1. Прямым решением уравнения

, показать, что векторы трансляций обратной решетки определяются формулами:

,

где i,j,k – циклические перестановки чисел 1, 2, 3.

Задача 2. Показать, что объем первой зоны Бриллюэна

, где

- объем элементарной ячейки решетки Бравэ.

Задача 3. Показать, что решетка, обратная к обратной, совпадает с исходной решеткой Бравэ.

Занятие 4.

Задача 1. Получить правильно нормированные однодетерминантные функции системы из N частиц с полуцелым спином (ферми-частицы)

Задача 2. Получить правильно нормированные однодетерминантные функции системы из N частиц с целым спином (бозе-частицы).

Задача 3. Получить выражение для энергии в методе Хартри-Фока через одноэлектронные функции системы N электронов, находящихся в поле ядер заряда

.

Задача 4. С помощью вариационного метода, используя функционал энергии, получить уравнения Хартри-Фока.

Задача 5. Показать, что уравнение Шредингера для периодической части волновой функции

можно записать в виде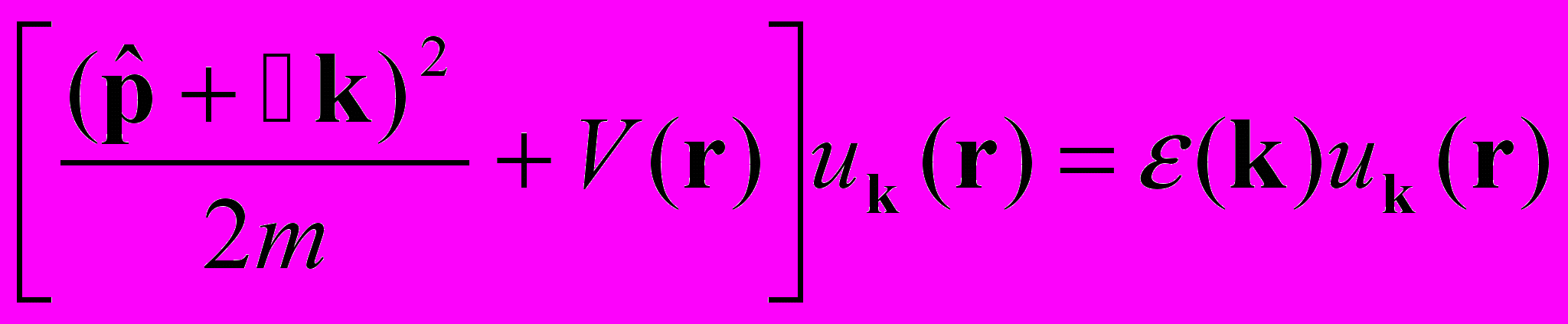

,

где

.

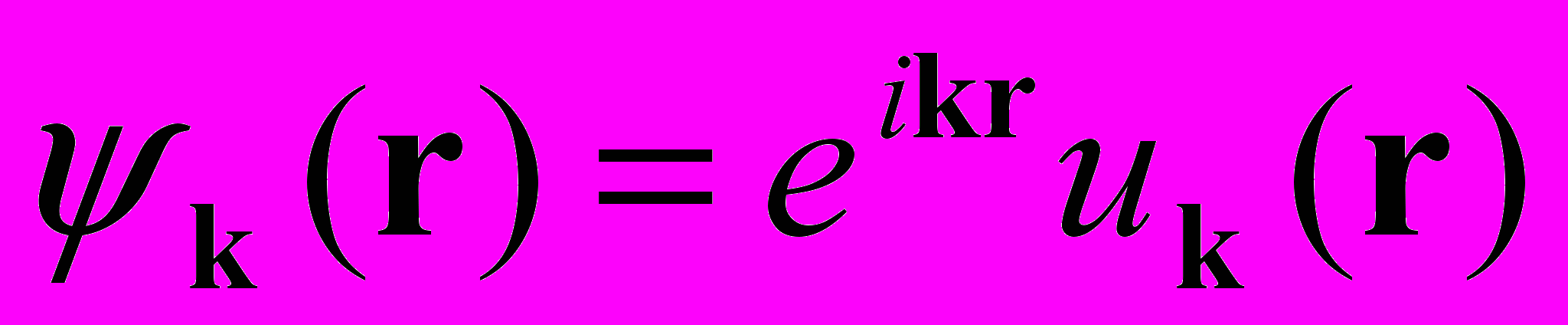Занятие 5.

Задача 1. Показать, что для одноатомного кристалла, функция, построенная как

,

где

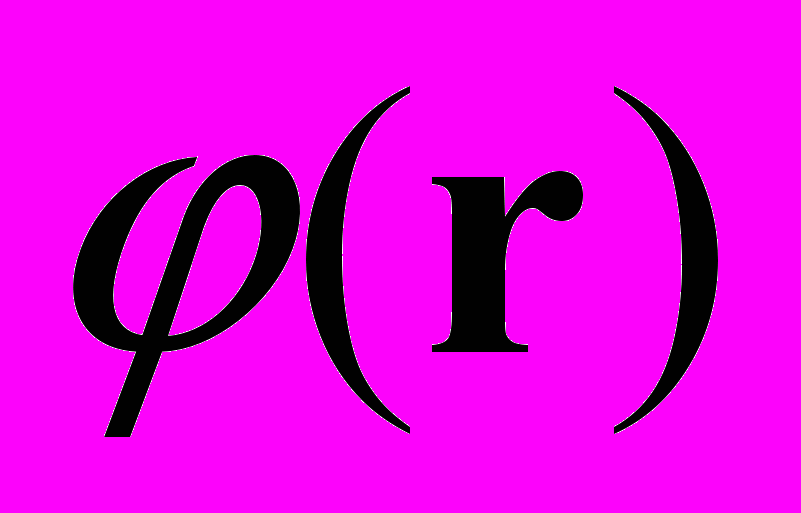- функции, локализованные в окрестности узлов решетки, является Блоховской функцией.

Задача 2. Рассмотреть одномерную модель кристалла с потенциалом вида:

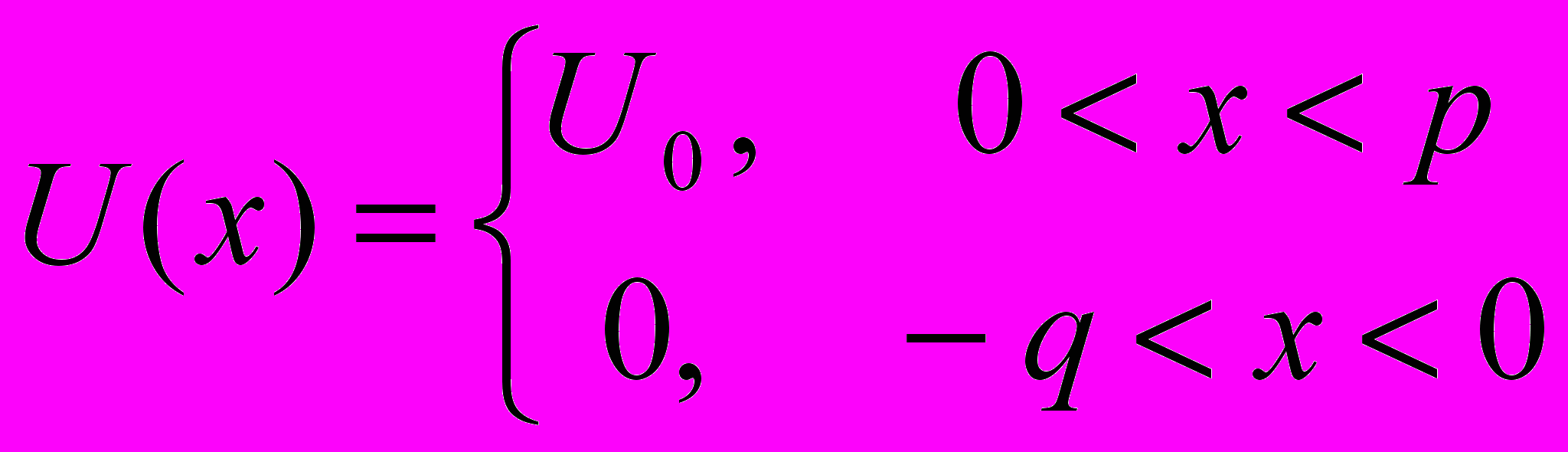
и периодом решетки

. Найти волновые функции, спектр энергий и рассмотреть предельный случай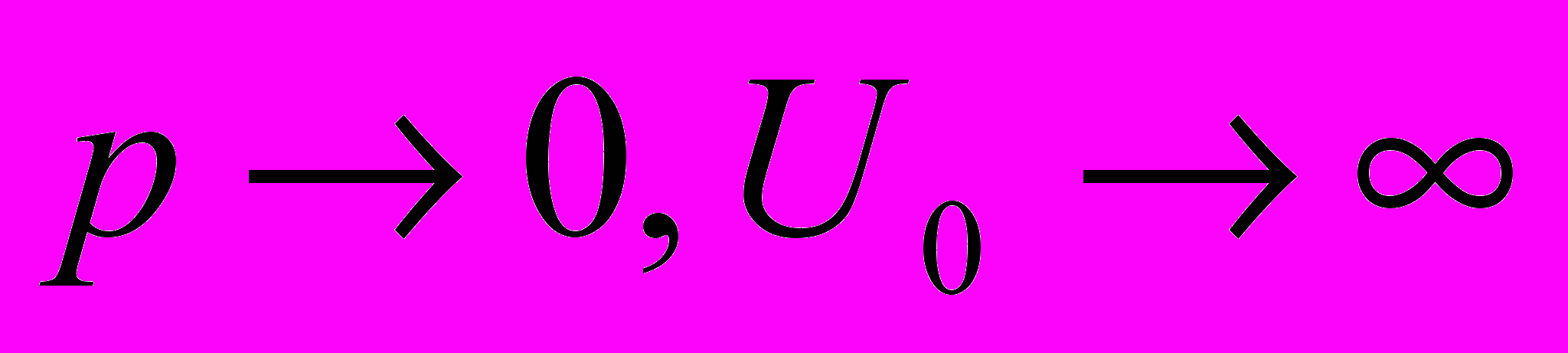

, так что

.

Занятие 6.

Задача 1. Используя метод плоских волн, найти спектр энергий в одномерном кристалле для значений волнового вектора на границе зоны Бриллюэна.

Задача 2. Показать, что на границах первой зоны Бриллюэна волновые функции свободного электрона в одномерной решетке с периодом d вырождены.

Задача 3. Рассмотреть задачу о 2-х мерном электронном газе и

а) показать, что кинетическая энергия электрона в «углу» зоны Бриллюэна в 2 раза больше, чем на середине стороны;

б) найти это отношение для 3-х мерного случая.

Занятие 7.

Задача 1. Показать, что для любого состояния электрона в кристалле групповая скорость в два раза больше фазовой скорости. Найти соотношение между групповой и фазовой скоростью, если закон дисперсии имеет вид

, а также показать, что

, если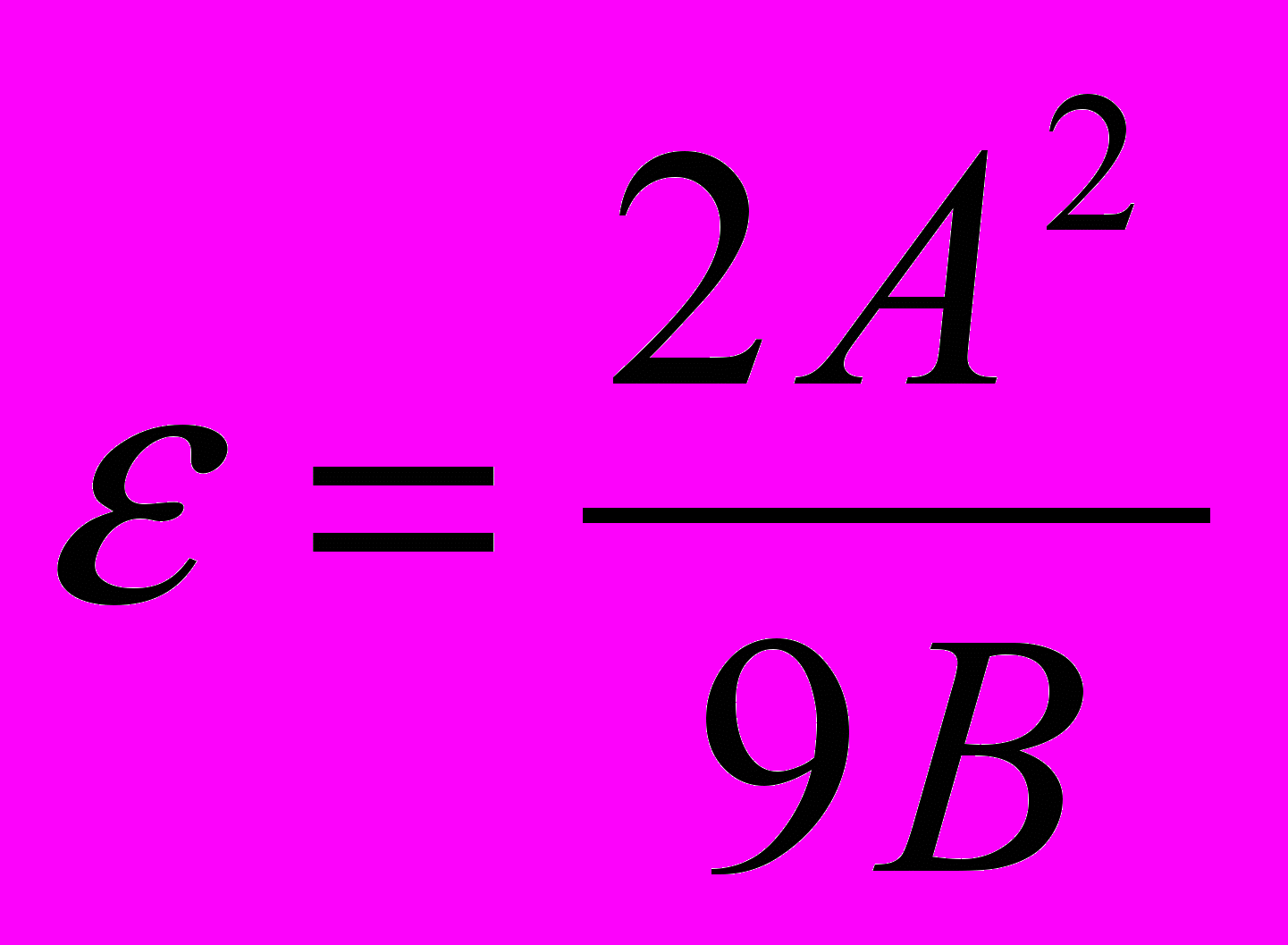

.

Задача 2. Показать, что для каждой энергетической зоны существует

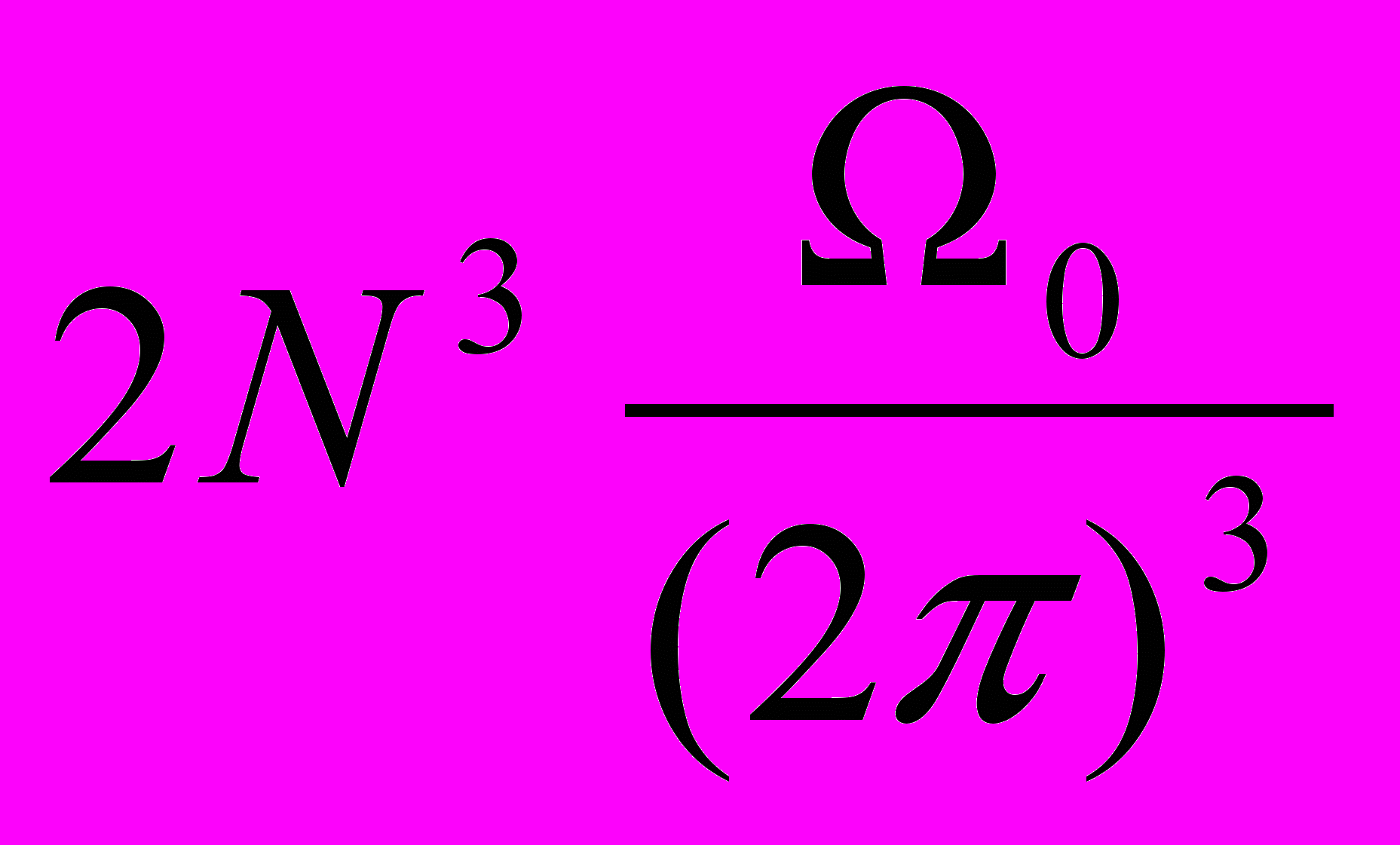состояний, приходящихся на единицу объема обратного пространства.

Занятие 8.

Задача 1. Доказать свойство «трансляции» функций Ваннье для одномерного случая :

, где n – номер узла одномерной решетки с периодом a.

Задача 2. Доказать ортогональность функций Ваннье

.

Задача 3. Вычислить функции Ваннье для случая простой кубической решетки, когда Блоховская функция задается плоской волной (электрон в пустой решетке).

Задача 4. Для простой кубической решетки с длиной ребра a вычислить 4 нижних энергии свободных электронов, если волновой вектор в схеме приведенных зон имеет длину

и перпендикулярен грани куба.

Задача 5. Используя выражение для энергии в методе сильной связи

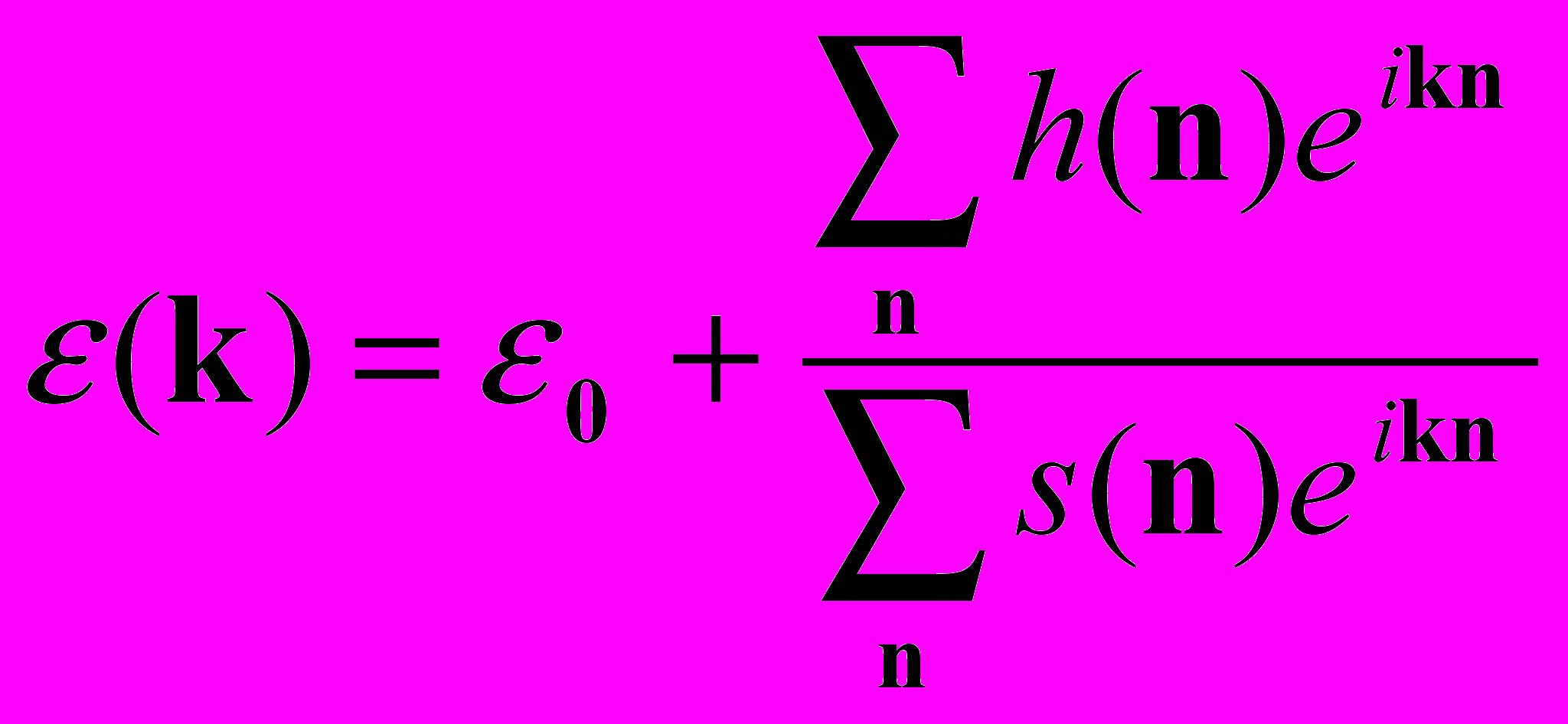
где

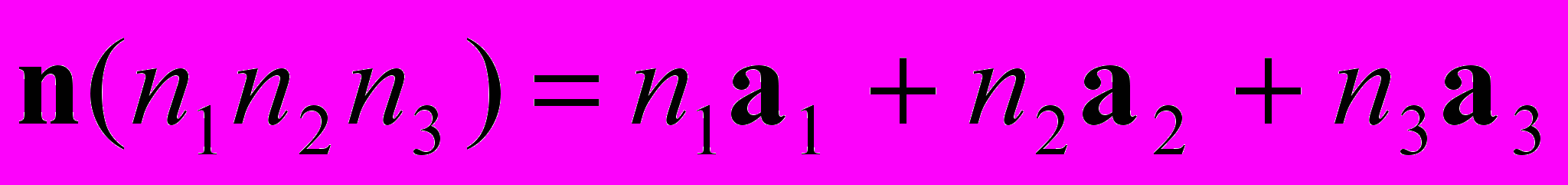, а также считая величины

параметрами, получить в приближении ближайших соседей явные выражения для функции

одноатомного кристалла с ПКР, ОЦК и ГЦК решеткой.

Задача 6. Получить выражение для тензора эффективной массы кристалла с простой кубической решеткой, если спектр энергий имеет вид

и найти предельные значения для точки

.

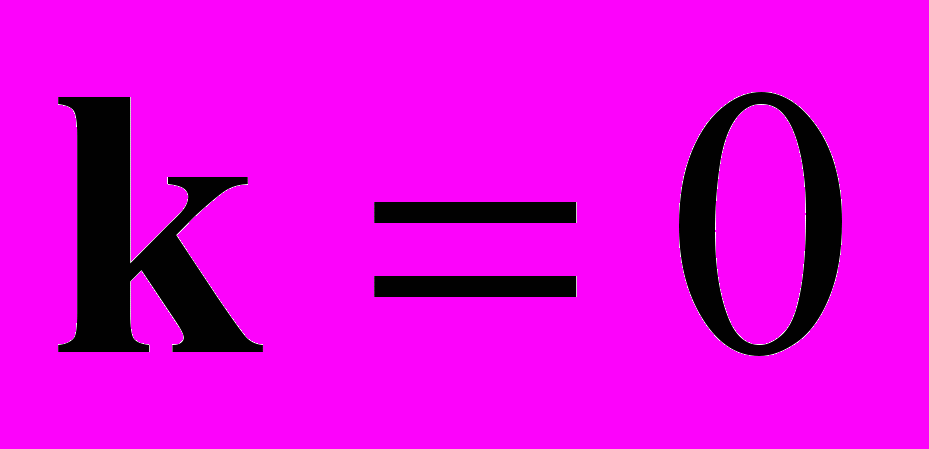4. Лабораторные занятия (не планируются)

Учебно-методические материалы по дисциплине

Список учебной литературы

Сведения об учебниках			Количество экземпляров в библиотеке на момент утверждения программы	Электронный вариант в библиотеке факультета
Наименование, гриф	Автор	Год издания		Электронный вариант в библиотеке факультета
Основная
1. Физика твердого состояния	Блэйкмор Дж.	1972 1988	1 6
2. Введение в физику твердого тела	Киттель Ч.	1978	4
3. Основы физики твердого тела	Зиненко В.И., Сорокин Б.П., Турчин П.П.	2001	5
4. Физика полупроводников	Бонч-Бруевич В.Л., Калашников С.П.	1977 1990	10 11
5. Теория твердого тела.	Давыдов А.С.	1976	9
6. Физика твердого тела	Павлов П.В., Хохлов А.В.	2000	10


Дополнительная:
7. Квантовохимические методы в теории твердого тела	Эварестов Р.А.	1982	15
8. Методы вычислительной физики в теории твердого тела	Барьяхтар В.Г., Зароченцев Е.В., Троицкая Е.Г.	1990	2
Учебные пособия
9. Моделирование элетронных состояний в кристаллах	Басалаев Ю.М., Гордиенко А.Б., Журавлев Ю.Н., Поплавной А.С.	2001	60

Учебно-методические пособия

Формы текущего, промежуточного и рубежного контроля

1. Вопросы и задания для индивидуальной и самостоятельной работы.

Дать определение решетки Бравэ.
Какие свойства являются общими для примитивной ячейки и ячейки Вигнера-Зейтца ? В чем заключаются их отличия ?
Является ли прямая решетка обратной по отношению к своей обратной ?
Как вычисляется объем элементарной ячейки ?
Как вычисляется объем ячейки Вигнера-Зейтца ?
Указать число первых и вторых соседей для простой кубической решетки.
Указать число ближайших соседей для гранецентрированной кубической решетки.
Указать число ближайших соседей для объемно-центрированной кубической решетки.
Изобразить плоскости [100], [110], [111] для простой кубической решетки.
За счет каких взаимодействий стабилизируется кристаллическая структура ионных кристаллов.
Может ли быть стабильным кристалл, атомы которого взаимодействуют только со своими ближайшими соседями ?
В чем состоит природа ковалентной связи.
Каков механизм водородной связи.
Привести примеры «скелетных» кристаллов и указать тип химической связи.
Описать природу взаимодействия Ван-дер-Ваальса.
Записать основное уравнение динамики решетки в гармоническом приближении.
Перечислить основные свойства решений уравнений динамики решетки.
В чем состоит отличие акустических колебаний от оптических.
Какой тип решеточных колебаний приводит к поляризации кристалла и почему.
Указать свойства волновой функции электронов в кристалле.
Сформулировать теорему Блоха.
Что называется Блоховской функцией ?
Какие типы квазичастиц могут существовать в кристаллах ?
В чем состоит механизм образования энергетических зон в кристаллах ?
Как зонная теория объясняет основное различие металлов и диэлектриков ?
Изобразить качественно схему энергетических зон полуметалла.
Записать соотношение, связывающее вектор скорости электрона и его волновой вектор.
Дать определение тензора эффективной массы. Какой вид имеет тензор в кубических кристаллах ?
Вычислить эффективную массу электрона в одномерном кристалле с законом дисперсии .
Вычислить эффективную массу электрона для закона дисперсии .
Дать определение плотности состояний.
В чем состоит механизм рассеяния электронов на колебаниях решетки.
Перечислить факторы, приводящие к рассеянию электронов в кристалле.
Чем отличаются волновая функция поверхностных состояний и волновая функция для идеального кристалла ?
Перечислить типы дефектов в твердых телах.
В чем состоит отличие дефекта по Френкелю от дефекта по Шоттки?
Изобразить частотную зависимость диэлектрической проницаемости для диэлектрика с ионной поляризацией и указать поляритонную область.
Указать основные свойства сверхпроводящего состояния.
Дать качественное описание механизма возникновения сверхпроводимости.
Сверхпроводимость : какие факторы указывают на определяющую роль колебаний решетки ?

2. Вопросы к экзамену (и зачету).

Основные понятия физики твердого тела: трансляционная симметрия, решетка Бравэ, основные векторы трансляций, элементарная ячейка, ячейка Вигнера-Зейтца.
Основные понятия физики твердого тела: обратная решетка, векторы трансляций обратной решетки, зона Бриллюэна.
основные понятия физики твердого тела: периодический потенциал, теорама Блоха (формулировка), зонная структура.
Элементарные возбуждения. Квазичастицы.
Общая формулировка квантовой задачи многих тел, многоэлектронное уравнение Шредингера.
Адиабатическое приближение. Разделение атомных и электронных координат.
Одноэлектронное приближение. Метод Хартри.
Антисимметричные волновые функции. Метод Хартри-Фока.
Определение и общие свойства электронной плотности.
Теория Функционала Плотности : первая теорема Хоэнберга-Кона.
Теория Функционала Плотности : вторая теорема Хоэнберга-Кона, вариационный принцип.
Метод Кона-Шэма. Функционал энергии. Обменно-корреляционная энергия.
Метод Кона-Шэма, уравнения Кона-Шэма.
Методы решения зонных уравнений: базисные функции, секулярное уравнение.
Метод плоских волн.
Метод ячеек.
Метод присоединенных плоских волн: МТ-потенциал.
Метод присоединенных плоских волн: решение зонного уравнения.
Общая схема линейного метода присоединенных плоских волн.
Метод ортогонализованных плоских волн.
Псевдопотенциал. Модельные и первопринципные псевдопотенциалы.
Электрон в пустой решетке. Зонная структура.
Приближение сильной связи: определение и общие свойства функций Ванье.
Приближение сильной связи – закон дисперсии, энергетические зоны в методе сильной связи.
Модель почти свободных электронов, теория возмущений. Зонная структура в схеме расширенных и приведенных зон.
Периодические граничные условия. Вычисление интегралов по зоне Бриллюэна.
Плотность состояний, вычисление для электрона в пустой решетке.
Свойства электронов в кристаллах: эффективная масса электронов и дырок, тензор эффективной массы.
Теорема Ванье.
Скорость электрона. Уравнения движения.
Электрон-фононное взаимодействие: общие свойства, тензор деформации, деформационный потенциал.
Вторичное квантование и представление чисел заполнение для деформационного потенциала.
Электрон-фононное взаимодействие – гамильтониана взаимодействия, диаграммы Фейнмана, элементарные процессы.
Виртуальные фононы.
Взаимодействие электронов с деформацией в случае сильной связи.
Электрон-фононное взаимодействие в ионных кристаллах. Полярон, модель Фрелиха.
Сверхпроводимость: критическая температура, эффект Мейснера-Оксенфельда. Уравнение Лондонов.
Сверхпроводимость, проникновение магнитного поля в сверхпроводиник.
Сверхпроводимость: теория Гинзбурга-Ландау.
Сверхпроводимость: длина когерентности, сверхпроводники 1-го и 2-го рода.
Квантование магнитного потока. Флюксон.
Основные положения микроскопической теории сверхпроводимости.
Виды взаимодействия света с твердым телом; оптические константы.
Собственное поглощение; экситонное поглощение; поглощение свободными носителями; примесное поглощение; решеточное поглощение.
Рекомбинационное излучение в полупроводниках. Межзонная рекомбинация.
Рекомбинация через локализованные центры. Экситонная рекомбинация. Твердотельные лазеры.
Общий теоретический анализ межзонных оптических переходов. дипольное приближение.
Вертикальные переходы, связь с оптическими константами.

4. Примерные темы рефератов, эссе.

Не планируется.

5. Контрольно-измерительные материалы.

Приложение 6.

Сведения о переутверждении РП на текущий учебный год и регистрация изменений

№ изменения	Учебный год	Содержание изменений	Преподаватель- разработчик программы	Рабочая программа пересмотрена и одобрена на заседании кафедры	Внесенные изменения утверждаю: Декан факультета:
				Протокол №_____ «__» _____ 200_ г.	«___» ________ 200_ г.
				Протокол №_____ «__» _____ 200_ г.	«___» ________ 200_ г.
				Протокол №_____ «__» _____ 200_ г.	«___» ________ 200_г.

Примечание:

Тексты изменений прилагаются к тексту рабочей программы обязательно.

В случае отсутствия изменений и дополнений вместо содержания изменений вносится запись «Принята без изменений».

1 Для специальности 511500 – радиофизика (Томский госуниверситет)

Blog