Государственным Образовательным Стандартом (гос) для обязательного изучения студентами специальности 010701. 65-физика, специализации "Теплофизика". Место и роль курса курс "Метод конечных элементов в задача
| Вид материала | Задача |
- Рабочая программа по философии для специальности 010701 «Физика» гсэ. Ф. 10. Физический, 485.77kb.
- Рабочая программа по курсу «Отечественная история» для специальность 010701 и направлению, 485.4kb.
- Рабочая программа дисциплины «нелинейные уравнения математической физики» Рекомендовано, 163.22kb.
- Учебная программа для студентов 3 курса очного отделения специальности 010701 «Физика», 193.43kb.
- Рабочая программа по курсу «Русский язык и культура речи» Для специальности 01. 07., 178.56kb.
- Методические указания к лабораторным работам по физике по практикуму «Вычислительная, 138.12kb.
- Учебная программа курса для специальности 050203. 65 Физика с дополнительной специальностью, 127.56kb.
- Рабочая программа учебной дисциплины (модуля) Метод конечных элементов и программы, 141.68kb.
- Учебно-методический комплекс по дисциплине Молекулярная физика для специальности 010701, 480.43kb.
- Рабочая программа дисциплины методы и средства радио- и дозиметрии рекомендована Методическим, 202.61kb.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Российский государственный университет им. И. Канта Факультет физико-технический
«Утверждаю»
Декан физико-технического факультета профессор, д.ф.-м.н. А.И. Иванов
_________________________________
“___”_______________ 2010 г.
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
В ЗАДАЧАХ ТЕПЛОПРОВОДНОСТИ
Учебная программа для студентов 4 курса очного отделения специальности 010701 «Физика» специализации «Теплофизика»
Программа составлена на основании типовой доцентом кафедры
“Прикладная физика” к.ф.-м.н. А.В. Румянцевым
Программа обсуждена и утверждена на заседании кафедры
“Прикладная физика”
Зав. кафедрой доцент , к.ф.-м.н. ______________________Н.М.Никулин
протокол № ___ от «__» ______________ 2010 г.
Программа одобрена методическим советом
физико-технического факультета протокол № __ от « » ______________ 2010 г.
Председатель методического совета
Доцент, к.ф.-м.н., __________ А.В. Пец
Пояснительная записка
СТАТУС КУРСА
Курс “Метод конечных элементов в задачах теплопроводности” ( СД. ДС. Ф.4 ) предусмотрен Государственным Образовательным Стандартом (ГОС) для обязательного изучения студентами специальности 010701.65-физика, специализации “Теплофизика”.
МЕСТО И РОЛЬ КУРСА
Курс “Метод конечных элементов в задачах теплопроводности” изучается в блоке специальных дисциплин СД. ДС специальности 010701.65-физика, специализации “Теплофизика” ГОСа. Знание наиболее эффективного численного метода решения краевых задач теплопроводности при наличии в многоэлементной системе сложного теплообмена необходимо при тепловом проектировании устройств любого назначения, в том числе, тепловых, электроракетных двигателей (ЭРД) и силовых энергоустановок (СЭУ). Читается в 7-м семестре с опорой на прочитанные ранее базовые спецкурсы из раздела ДС: “Теплообмен излучением”, “Теория теплопроводности”. Он является завершающим циклом из курса ОПД, “Дифференциальные уравнения” (численные методы решения), “Методы математической физики“ и др. Целью курса является подготовка студентов к пользованию получившими широкое распространение обобщенными программами «NISA», «ANSYS» и др., базирующимися на численном методе конечных элементов (не только в задачах теплопроводности).
Программа дисциплины представляет собой теоретические и практические описания алгоритма использования метода конечных элементов, общего для краевых задач любого физического содержания, таких, как расчет: поля скоростей в гидрогазодинамике, магнитного поля, прочностных задач и т.д. По освоении курса студент (аспирант) приобретает соответствующие общим требованиям ГОС и целям ООП знания, умения и навыки, позволяющие грамотно пользоваться программами численного расчета, базирующимися на методе конечных элементов в его различных формулировках.
ТРЕБОВАНИЯ К НАЧАЛЬНОЙ ПОДГОТОВКЕ
Для успешного освоения курса необходимо знание: курсов общей физики и высшей математики: интегрального и дифференциального исчисления; методов решения дифференциальных уравнений; методов математической физики; а так же курсов: основы механики сплошных сред.
ЦЕЛИ И ЗАДАЧИ КУРСА
ЦЕЛЬ КУРСА – подготовка студентов к пользованию получившими широкое распространение обобщенными программами «NISA», «ANSYS» и др., базирующимися на численном методе конечных элементов в задачах: организации теплового режима объекта; расчета 3-х мерного магнитного поля; прочностных; гидрогазодинамических и т.д.
ЗАДАЧИ КУРСА – формирование алгоритма программ, базирующихся на МКЭ; умение физически грамотного задания краевых условий задачи; развитие навыков: дискретизации области определения; получения стандартизованных матриц; а так же развитие познавательных интересов, интеллектуальных и творческих способностей в процессе приобретения знаний по физике с использованием различных источников информации и современных информационных технологий.
СТРУКТУРА УЧЕБНОЙ ДИСЦИПЛИНЫ
Структура и содержание курса обусловлено требованиями ГОСа по специальности 010701.65-физика, соответствует основным монографиям по МКЭ. Основные дидактические единицы, изучаемые в данном курсе: конечный элемент; невязка; взвешенная невязка; дискретизация области определения; уравнение переноса; краевые условия; элементный вклад; базисная функция; сокращенная и глобальная матрицы; метод Галеркина; стандартизованные матрицы: теплопроводности – объемная и поверхностная, теплоемкости; векторы тепловой нагрузки – объемный и поверхностный; базовый каталог объемных элементов.
Предусмотрено: чтение лекций, практические занятия по решению задач, задания на самостоятельную работу. Текущий контроль знаний студентов осуществляется в течение семестра на практических занятиях.
Форма заключительного контроля – зачет в 7-м семестре. Условие допуска к зачету – предъявление результатов выполнения всех заданий на самостоятельную работу.
ПЕРЕЧЕНЬ ПРОФЕССИОНАЛЬНЫХ КОМПЕТЕНЦИЙ, КОТОРЫЕ ДОЛЖЕН ПОЛУЧИТЬ СТУДЕНТ В ПРОЦЕССЕ ОБУЧЕНИЯ
| ТЕМА | ОСНОВНЫЕ ЗНАНИЯ, УМЕНИЯ И НАВЫКИ |
| Геометрические аспекты МКЭ Математическое описание элемента Задание краевых условий задачи Решение системы динамических уравнений | Разбиение области определения задачи на конечные элементы, соответствующие геометрии области; индексация и нумерация узлов элементов с соблюдением требования минимизации полуширины матриц. Формирование геометрической части таблицы входных данных. Получение базисных функций для элементов базового каталога конечных элементов. Получение стандартизованных матриц и векторов тепловой нагрузки. Задание: теплофизических свойств элементов по физическому каталогу; механизмов теплообмена; распределения внутренних и внешних динамических потоков по элементам; начального температурного поля. Формирование рекуррентного уравнения. Псевдоитерационный метод его решения. Учет температурной зависимости теплофизических свойств элементов. |
РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ РАЗЛИЧНЫХ ВИДОВ УЧЕБНЫХ ЗАНЯТИЙ
В Государственном Образовательном Стандарте по данной дисциплине предусмотрено: чтение курса лекций, проведение практических занятий и заданий на самостоятельную работу. При разработке курса лекций рекомендуется обращать внимание на практическое применение МКЭ к расчету тепловых режимов конкретных конструкций. Особое внимание следует обращать на те разделы программы, которые далее используются в других дисциплинах учебного плана.
При проведении практических занятий необходимо отработать навыки по разбиению области определения на элементы; грамотной нумерации узлов; математическому описанию элемента с тестовой проверкой полученных функций; формирования таблицы входных данных. Практические занятия должны заложить основу, достаточную для выполнения заданий на самостоятельную работу. ГОСом по курсу предусмотрен ЗАЧЕТ в 7-м семестре.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ СТУДЕНТАМ
ПО ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. При конспектировании лекций оставляйте на листе достаточно широкие поля для заметок и дополнений при последующей проработке лекционного материала. После лекции следует внимательно проработать свой конспект, в случае необходимости дополнить его, используя основную и дополнительную литературу. Если в литературе Вы не нашли ответов на свои вопросы, обратитесь к своему преподавателю во время консультаций или в перерывах между занятиями. Обязательно выделите в своём конспекте формулировки основных законов и основные формулы.
2. Темы курса, выносимые на самостоятельную проработку, изучайте, пользуясь списком дополнительной литературы.
3. После семинарских занятий обязательно разберите ход решения задач, дополните решения, в случае необходимости запишите в тетради условия задачи. Если Вы не можете самостоятельно вспомнить подробно решение задачи, задайте свои вопросы преподавателю на следующем семинарском занятии. После этого на чистом листе бумаги решите эти же задачи. Через некоторое время попробуйте решить те же задачи самостоятельно.
4. При подготовке к зачёту или экзамену используйте тексты заданий, которые Вы получали на каждом семинарском занятии. Для начала решите демонстрационный вариант теста, который был разобран на последнем семинарском занятии. После этого выборочно решайте задачи из разных разделов самостоятельно.
5. Перед экзаменом ( или зачётом ) хорошо отдохните, на экзамене не волнуйтесь, максимально мобилизуйте свои умственные способности.
Методические рекомендации для преподавателей
В начале чтения курса необходимо вспомнить некоторые разделы курса общей физики и математики, которые изучались студентами на предыдущих курсах.
При чтении лекционного курса особое внимание следует обращать на физику происходящих процессов, возможности применения тех или иных приближенных теорий, их связь с ранее изученными теориями. Значительное место в курсе должно быть отведено использованию полученных формул для практических расчётов тепловых режимов.
СОДЕРЖАНИЕ ПРОГРАММЫ КУРСА
Введение
Общая характеристика предмета курса, его связь с другими курсами теплофизической направленности, цели и задачи курса, его предназначение.
Краевые задачи теории поля
Уравнение переноса в обобщённой криволинейной системе координат. Краевые условия задачи. Краткая характеристика методов решения краевой задачи.
Метод конечных элементов в краевых задачах теории поля
Методы взвешенных невязок. Основная концепция метода конечных элементов.
Его преимущества по сравнению с другими вычислительными методами в формулиров-
ке метода Галеркина.
Геометрические аспекты МКЭ
Базовый каталог конечных элементов. Дискретизация области на элементы. Нумерация элементов и узлов. Индексация узлов и формирование таблицы входных данных.
Математическое описание элемента
Метод Крамера. Метод Лагранжа. Обобщенный метод Крамера-Лагранжа. Свойства базисных функций. Необходимые и достаточные условия для тестовой проверки правильности полученных базисных функций.
Вычислительные аспекты МКЭ
Общее решение краевой задачи методом Галеркина. Матричное представление элементного вклада. Формирование глобальных матриц. Стандартизация матриц элемента. Средние – объемная и поверхностная – температуры элемента.
Программная реализация метода конечных элементов
Задание краевых условий задачи. Решение системы динамических уравнений псевдоитерационным методом. Учёт температурной зависимости свойств элемента. Конвективный компонент теплообмена. Радиационный компонент теплообмена.
Базовый каталог объемных конечных элементов
Методика получения стандартизованных матриц элемента (конкретный пример для 2-го элемента базового каталога)
Темы семинарских занятий
| № п/п | Темы семинарских занятий | Количество часов | |
| 1 | 2 | 3 | |
| 1 2 3 4 5 | Температурное поле. Уравнение теплопроводности как частный случай уравнения переноса. Физический смысл краевых условий. Механизмы теплообмена – кондуктивный, конвективный, радиационный. Их особенности и описывающие их законы. Краевые условия 1-го, 2-го, 3-го и 4-го родов. Аналитические методы решения дифференциального уравнения 2-го порядка в частных производных: метод разделения переменных; операционный метод Лапласа. Недостатки аналитического метода решения краевой задачи. Методика решения краевой задачи методом взвешенных невязок в формулировке Галеркина (конкретный пример). Дискретизация области определения на элементы. Нумерация элементов; индексация и нумерация узлов с соблюдением критерия минимизации полуширины матрицы. Базовый каталог конечных элементов. Принцип его построения. Получение базисных функций элемента. Их свойства. | 2 4 4 4 8 | |
| 1 | 2 | 3 | |
| 6 7 8 9 | Матричное представление элементного вклада. Получение числовых матриц объемной и поверхностной теплопроводности для одного из элементов базового каталога. Получение числовой матрицы теплоемкости для элемента. Получение числовых матриц тепловых нагрузок – объемной и поверхностной для элемента. Вычисление объемной и поверхностных температур элемента базового каталога. | 6 2 4 2 | |
| Итого: | 36 | ||
Тематический план курса
| Темы учебных занятий | Лекц. | Практ. | Самост. | КСР |
| 1 | 4 | 5 | 6 | 7 |
| Введение Общая характеристика предмета курса, его связь с другими курсами теплофизической направленности, цели и задачи курса, его предназначение. Краевые задачи теории поля. Уравнение переноса в обобщённой криволи- нейной системе координат. Краевые условия задачи. Краткая характеристика методов решения краевой задачи. Метод конечных элементов в краевых задачах теории поля. Методы взвешенных невязок. Основная концепция метода конечных элементов. Геометрические аспекты МКЭ. Базовый каталог конечных элементов. Дискретизация области на элементы. Нумерация элементов и узлов. Индексация узлов и формирование таблицы входных данных. Математическое описание элемента. Метод Крамера. Метод Лагранжа. Обобщенный метод Крамера-Лагранжа. Свойства базисных функций. Вычислительные аспекты МКЭ. Матричное представление элементного вклада. Формирование глобальных матриц. Стандартизация матриц элемента. Средние температуры элемента. Программная реализация МКЭ. Задание краевых условий задачи. Решение системы динамических уравнений. Учёт температурной зависимости свойств элемента. Конвективный и радиационный компоненты теплообмена. | 2 4 4 8 12 12 12 | 4 4 4 8 6 8 2 | 2 4 4 8 12 6 | |
| Итого: | 54 | 36 | 36 | 12 |
Задания на самостоятельную работу
Задание 1
1.1 Получите выражения уравнения переноса (1.1.14) в декартовой,
цилиндрической и сферической системах координат S = 1,2,3.
1.2 Проделайте эту же операцию для граничных условий (1.2.7).
Задание 2
2.1 На основании формул п. 2.1 получите методами коллокаций и Ритца приведенные в таблице данные.
2.2 В приведенном в п. 2.1 примере понизьте на единицу степень полинома и получите решение методом Галеркина. Сравните с данными в таблице и сделайте выводы.
2.3 Используя метод Галеркина, найдите решение уравнения
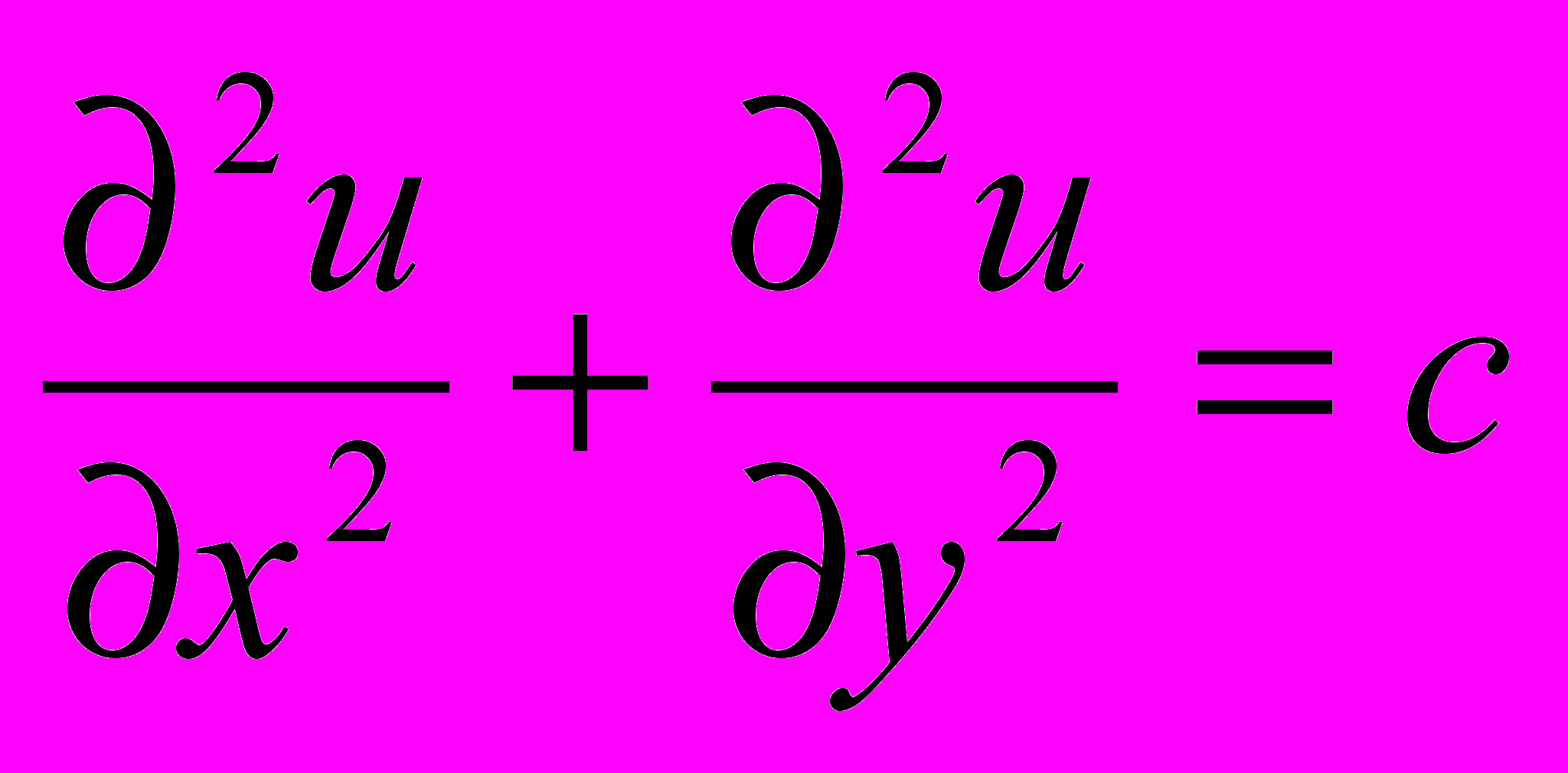
с граничными условиями
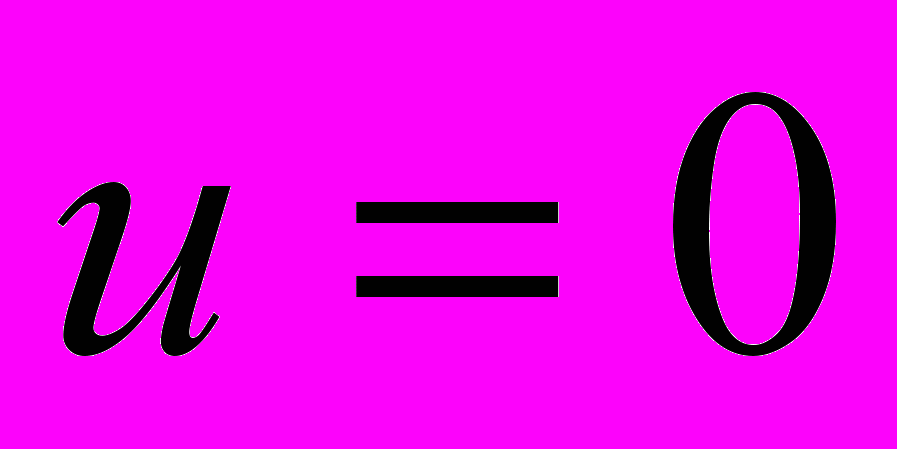при 
, 
. При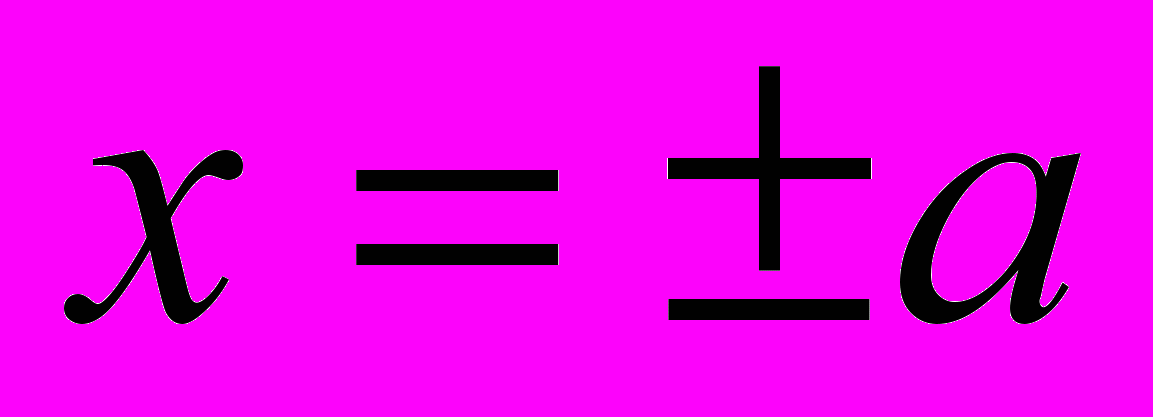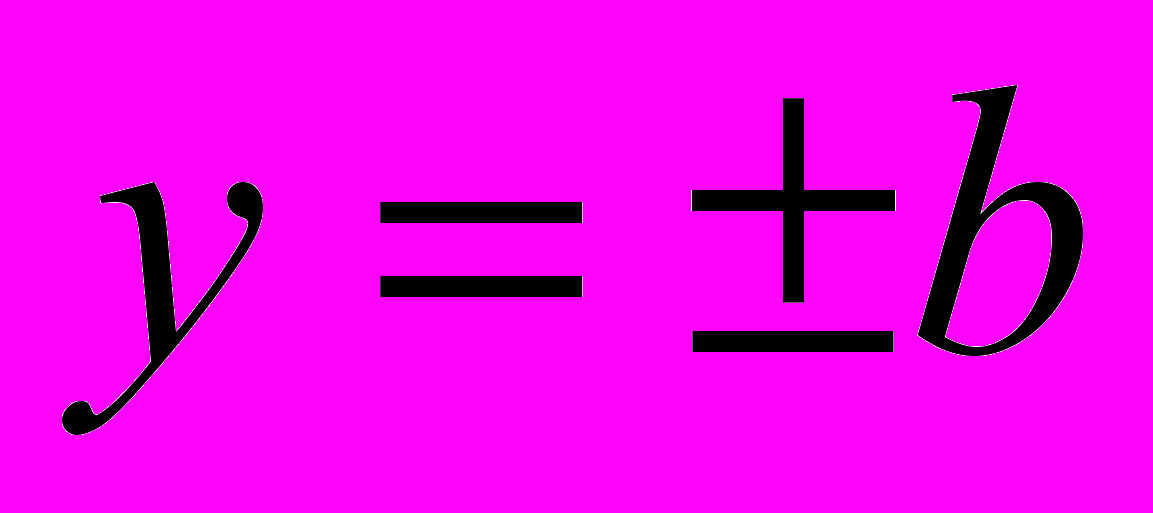мите в первом приближении 
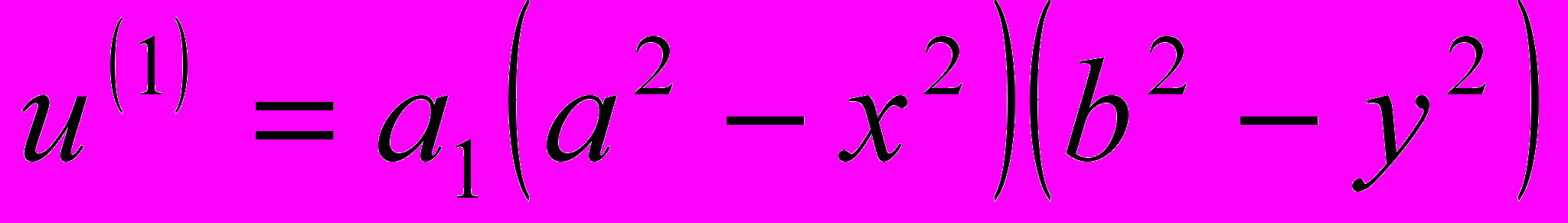.2.4 Найдите приближенные значения
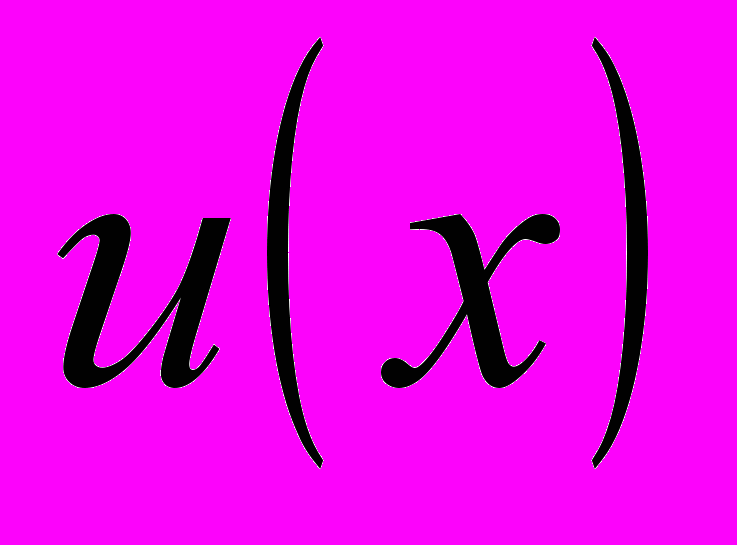, удовлетворяющей дифференциальному уравнению:
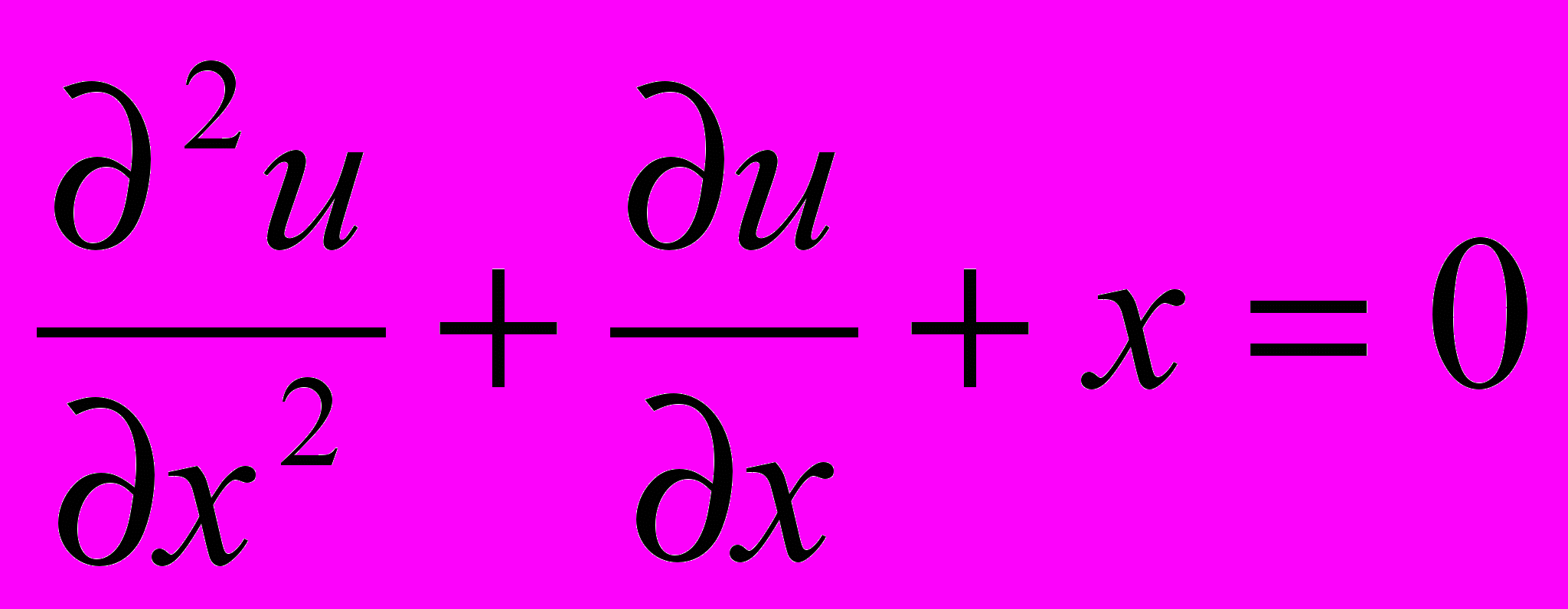, при
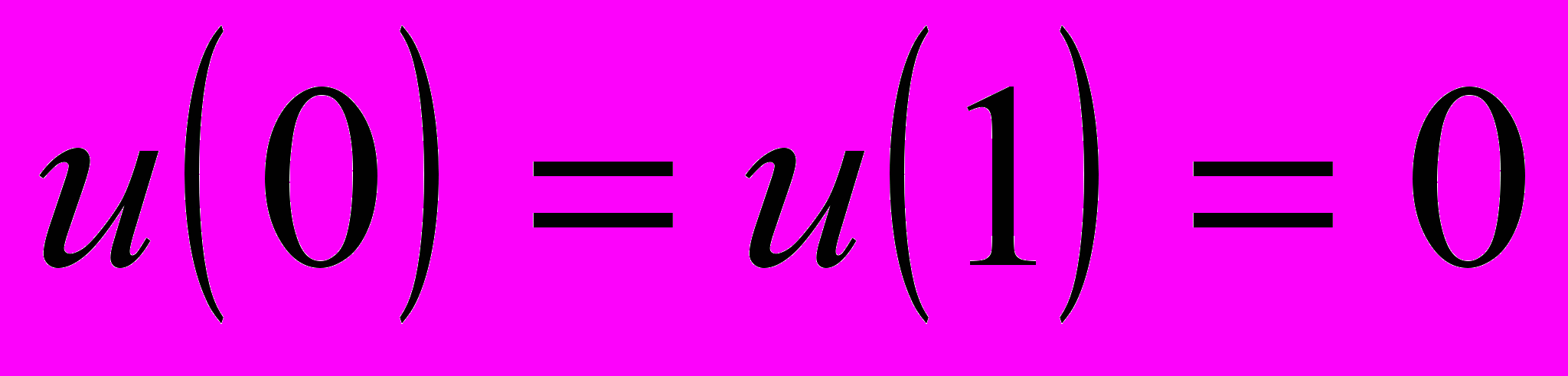и изменении 
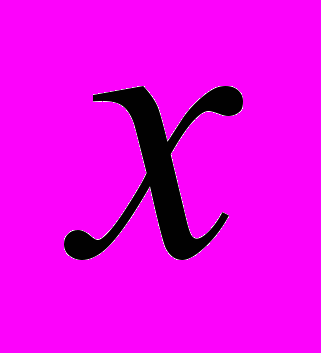в интервале 0 ÷ 1. Примите 
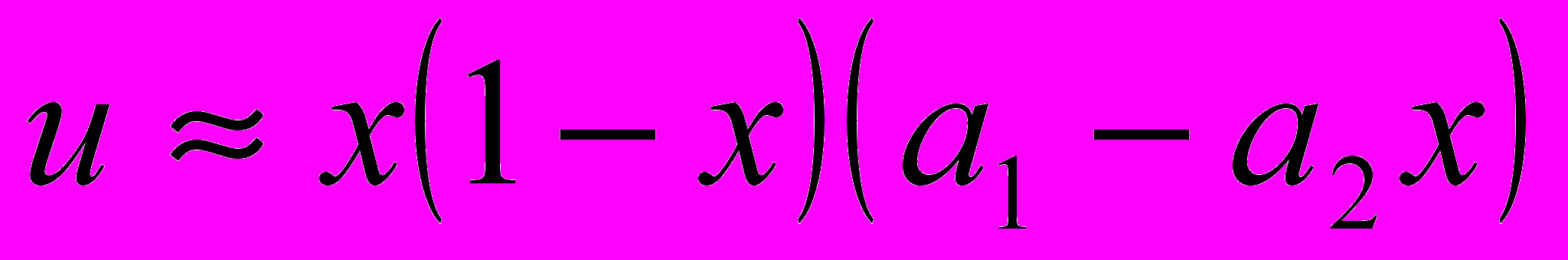.Задание 3
3.1 Дискретизируйте объект – треугольную прямую призму – на два неодинаковые по размерам элемента. Задайте координаты узлов; составьте таблицу входных данных.
3.2 Дискретизируйте делением по углу и по длине на 4 элемента объект, представляющий собой четверть (по углу
) полого цилиндра. Задайте координаты узлов; составьте таблицу входных данных.3.3 Какие свойства материала элемента следует внести в физический каталог в задачах теплопроводности?
Задание 4
4.1 Найдите базисные функции для элементов:
а)
; 
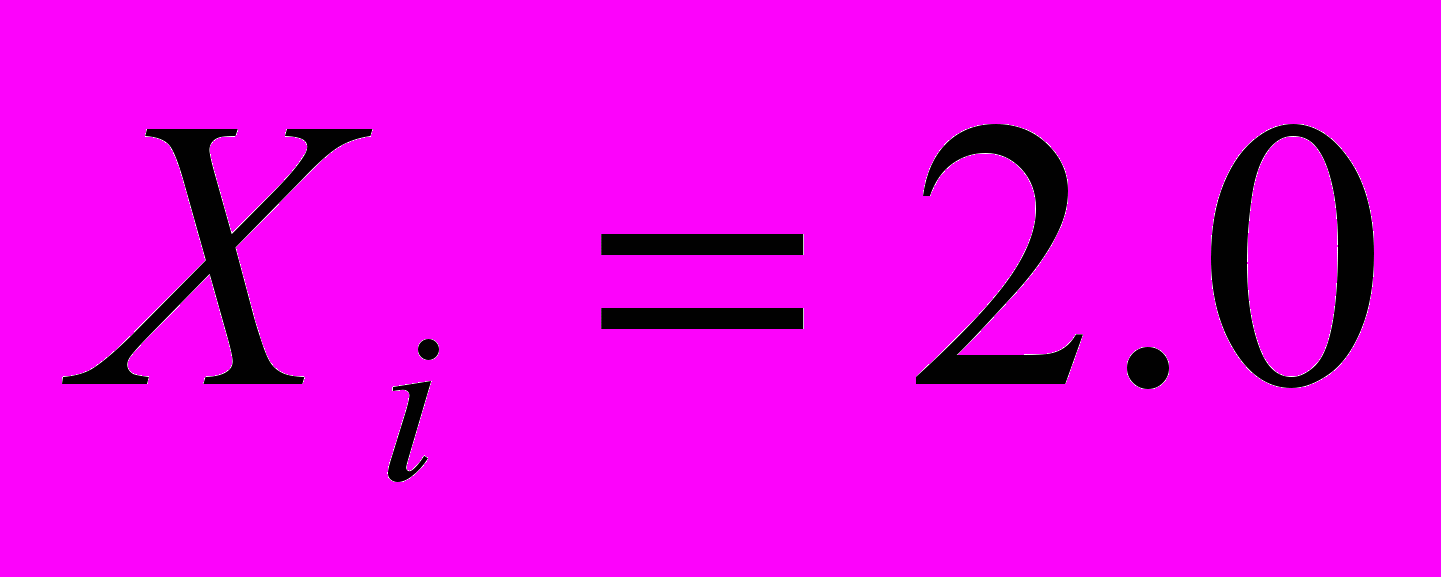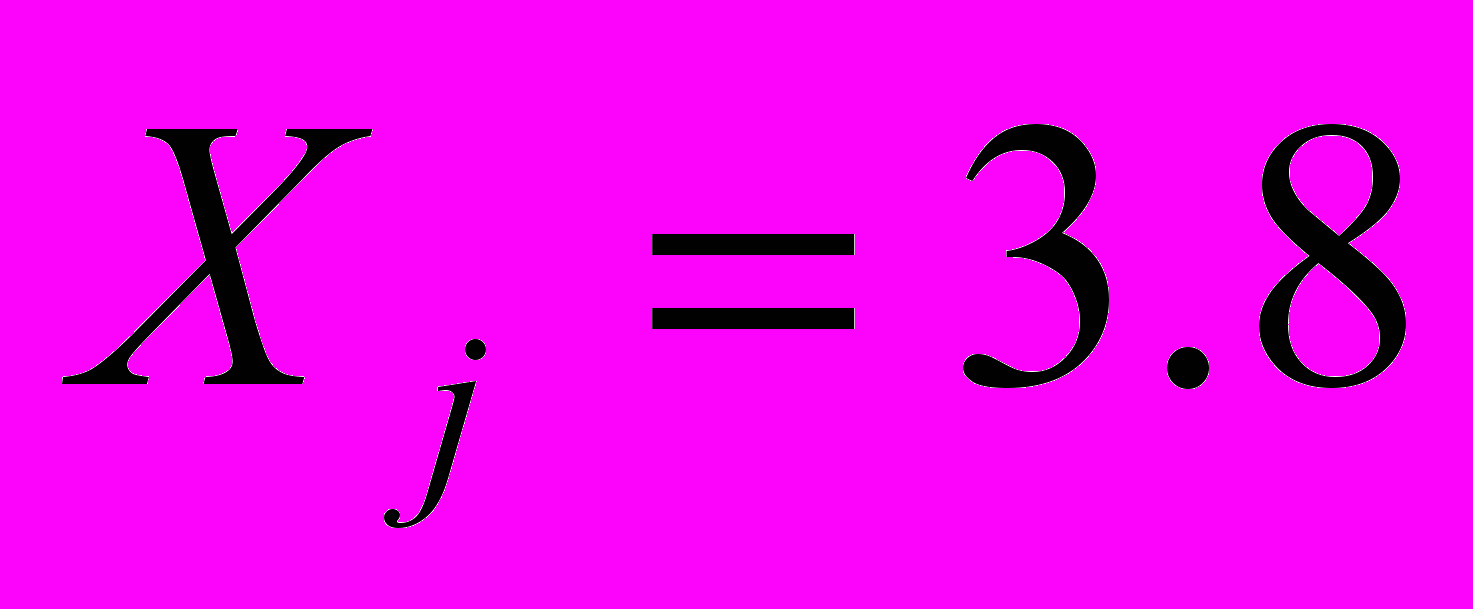; б)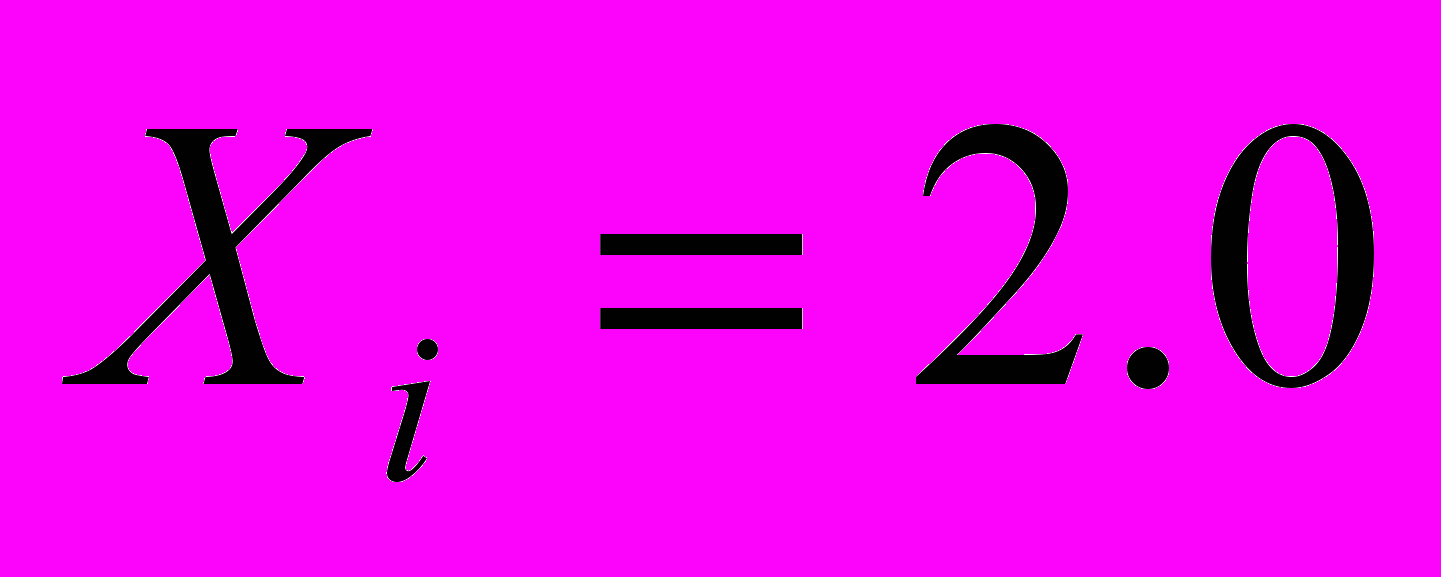
; 
; 
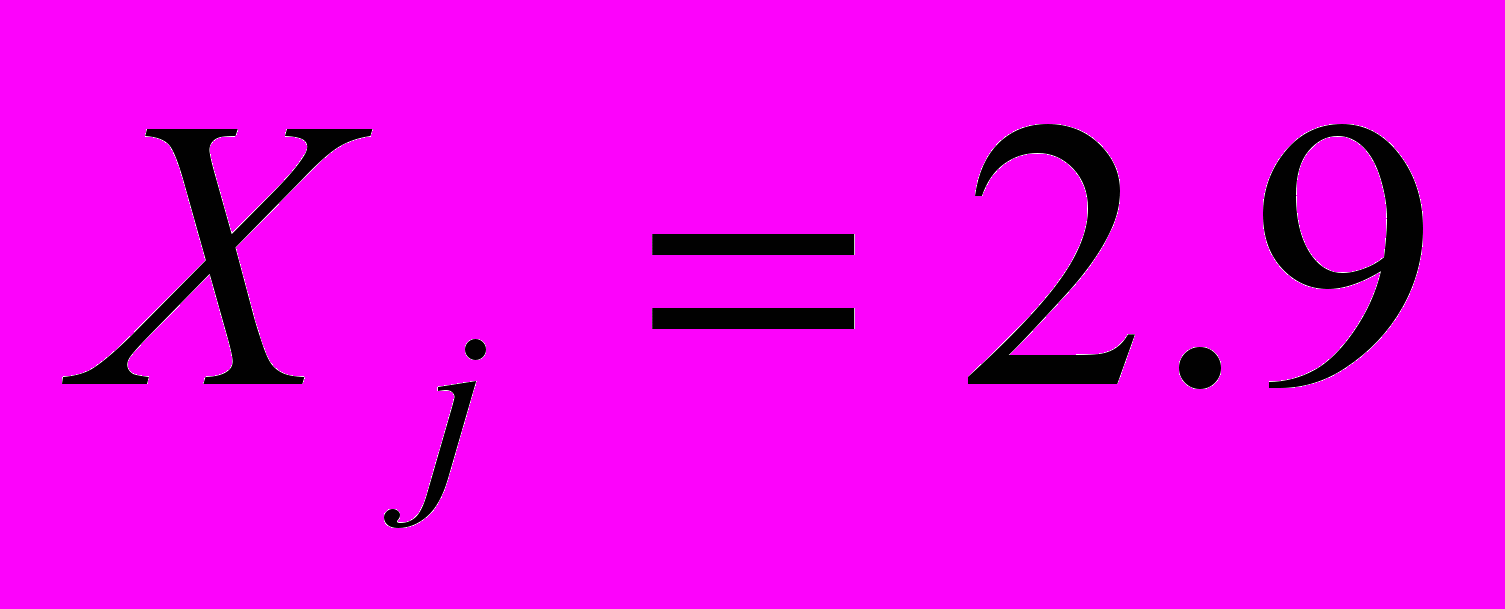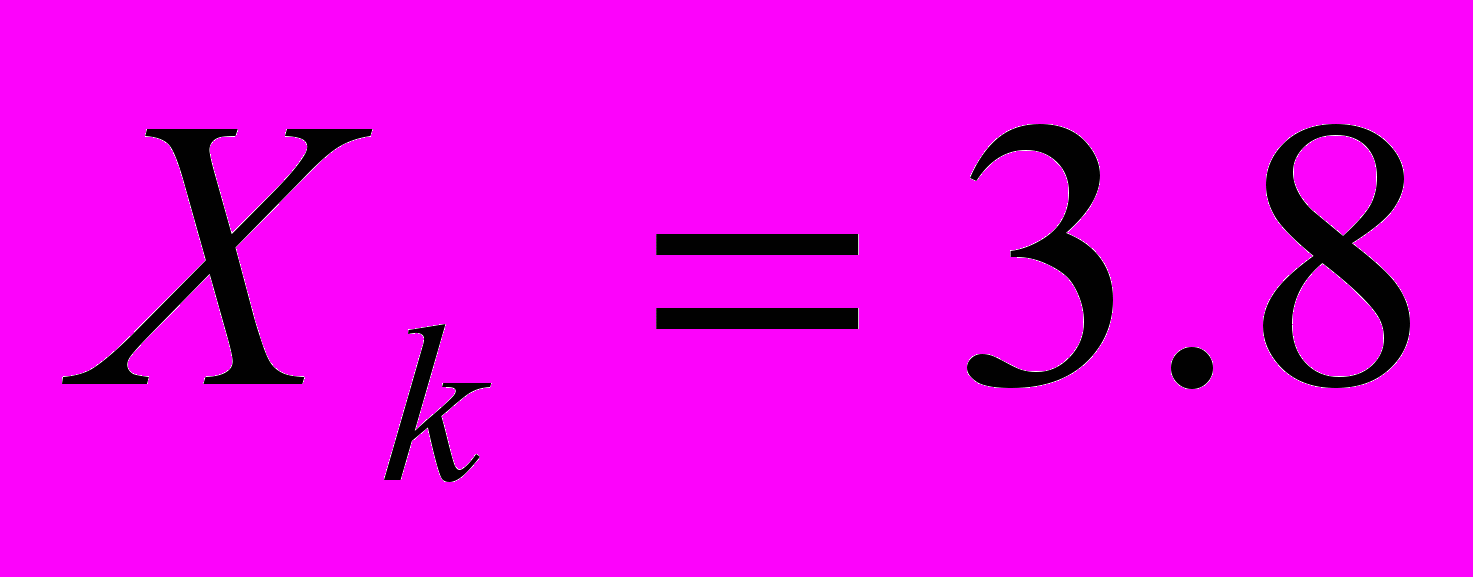;в)
; 
; 
; 
; 
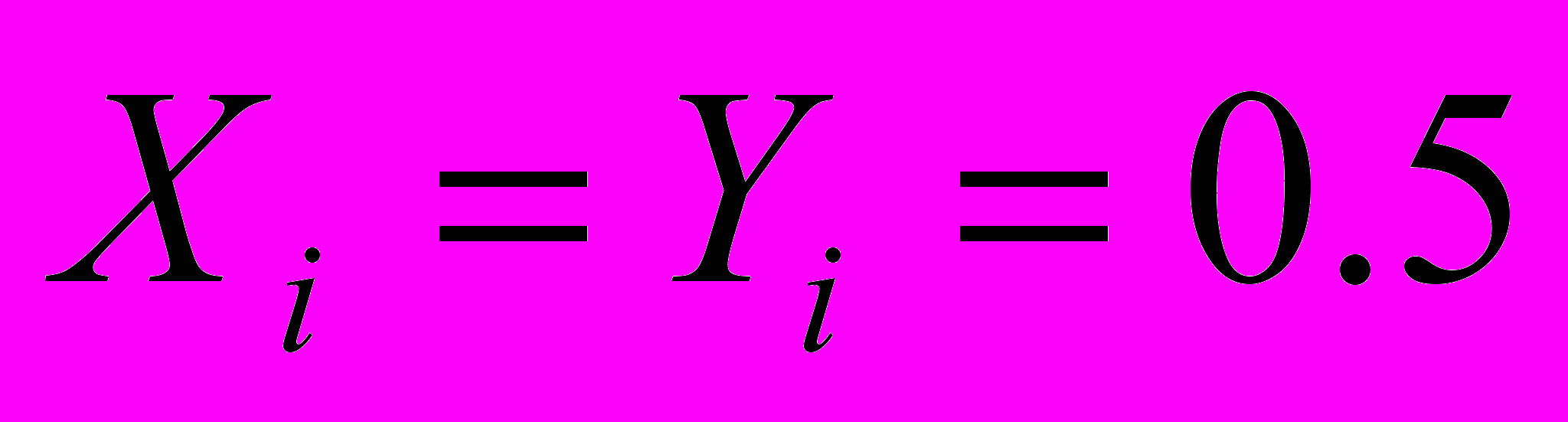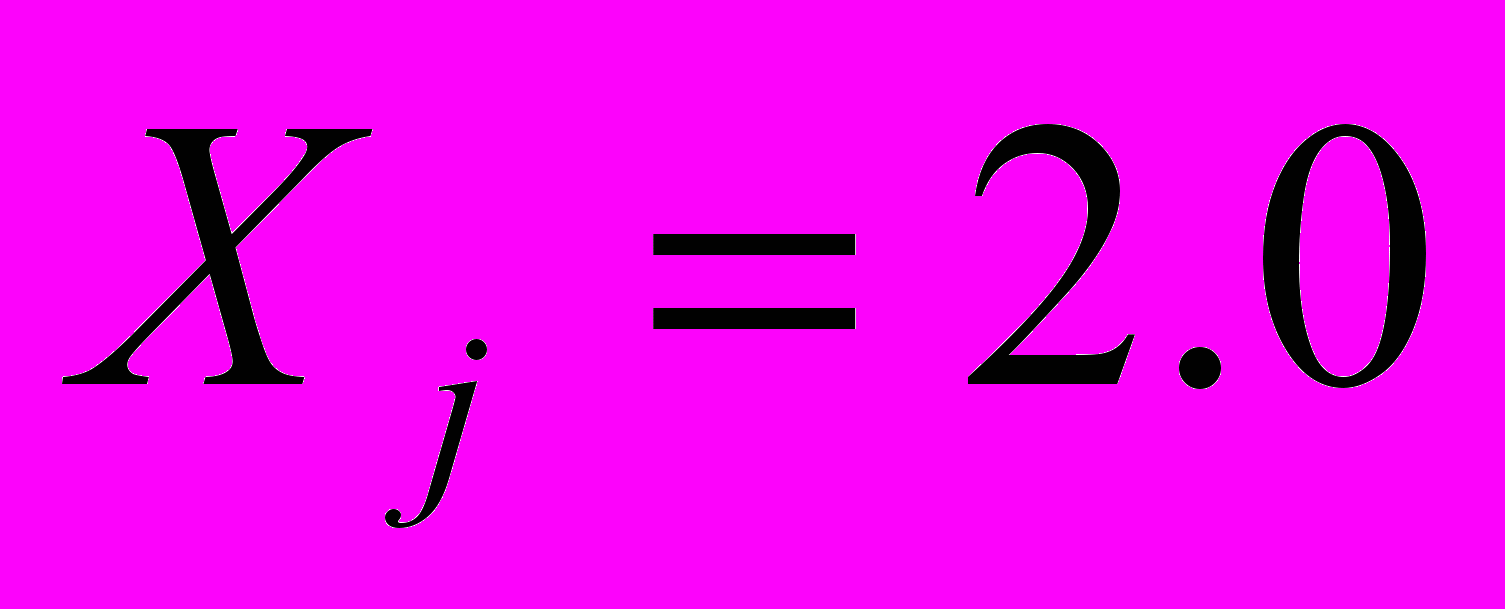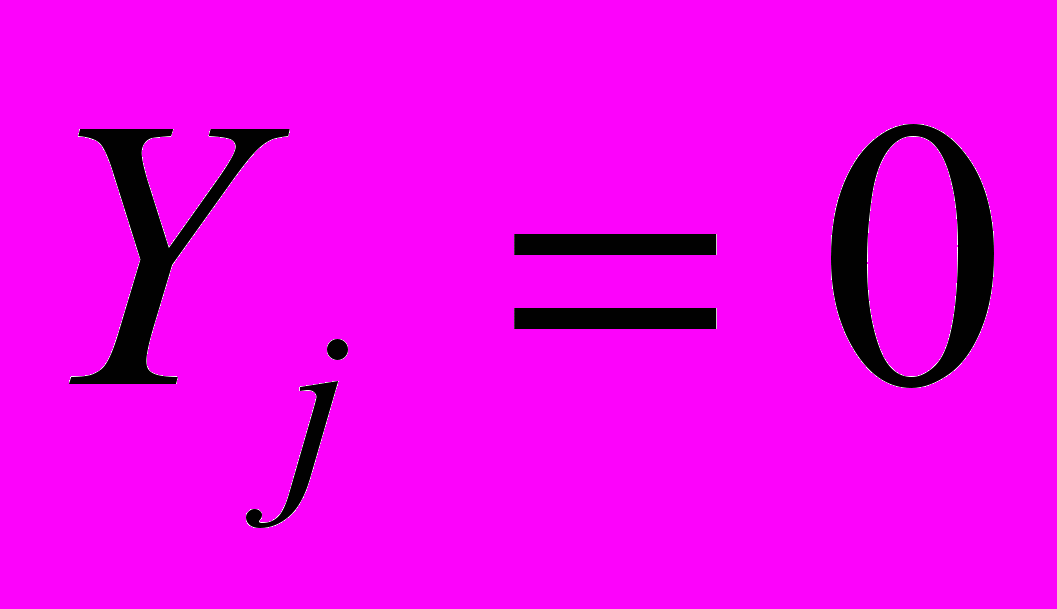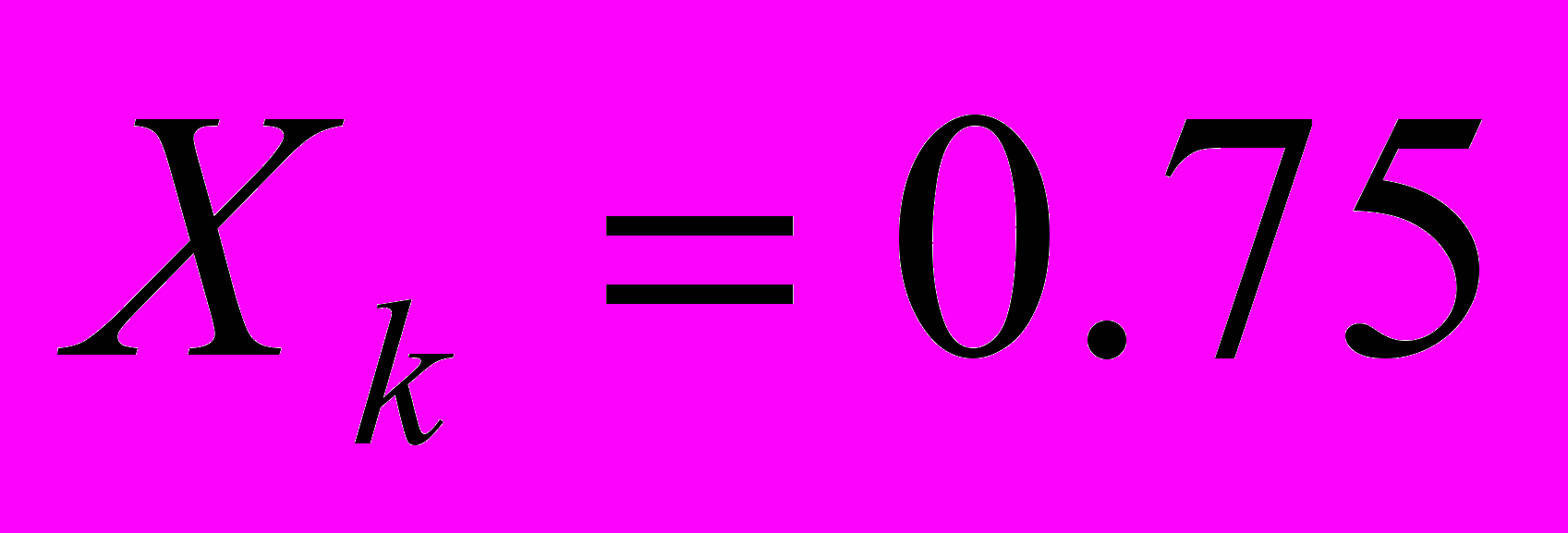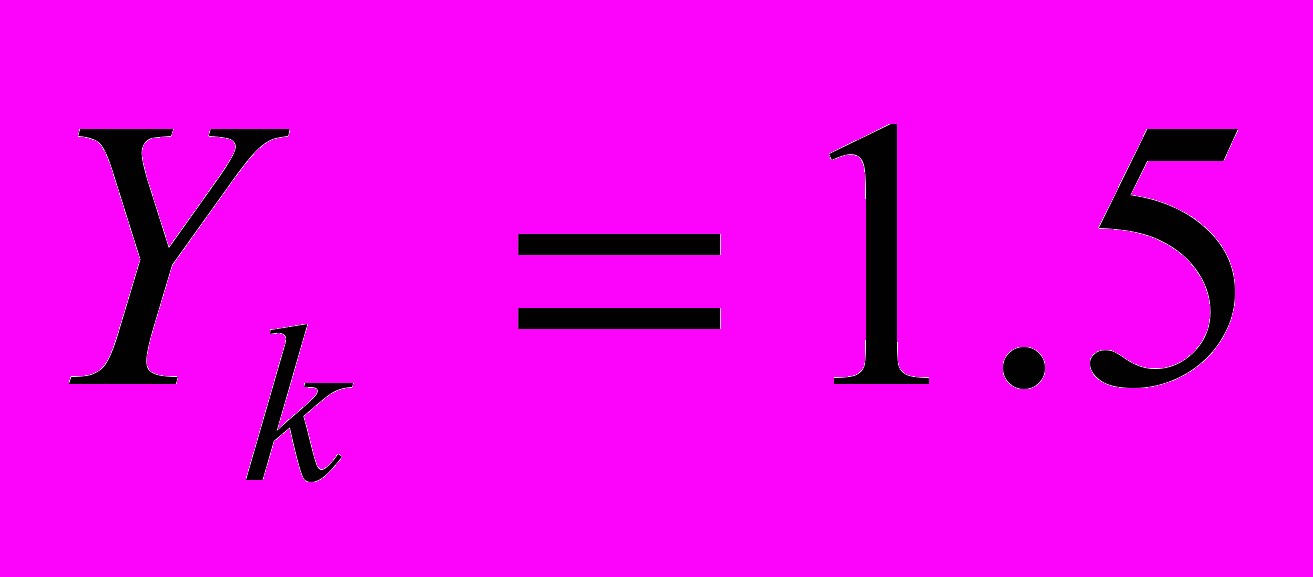; г) докажите справедливость найденных выражений для всех базисных функций;4.2 Покажите, что для симплекс-треугольника Ni(x,y) = 0 в узлах j и k.
4.3 Покажите, что базисная функция треугольного элемента
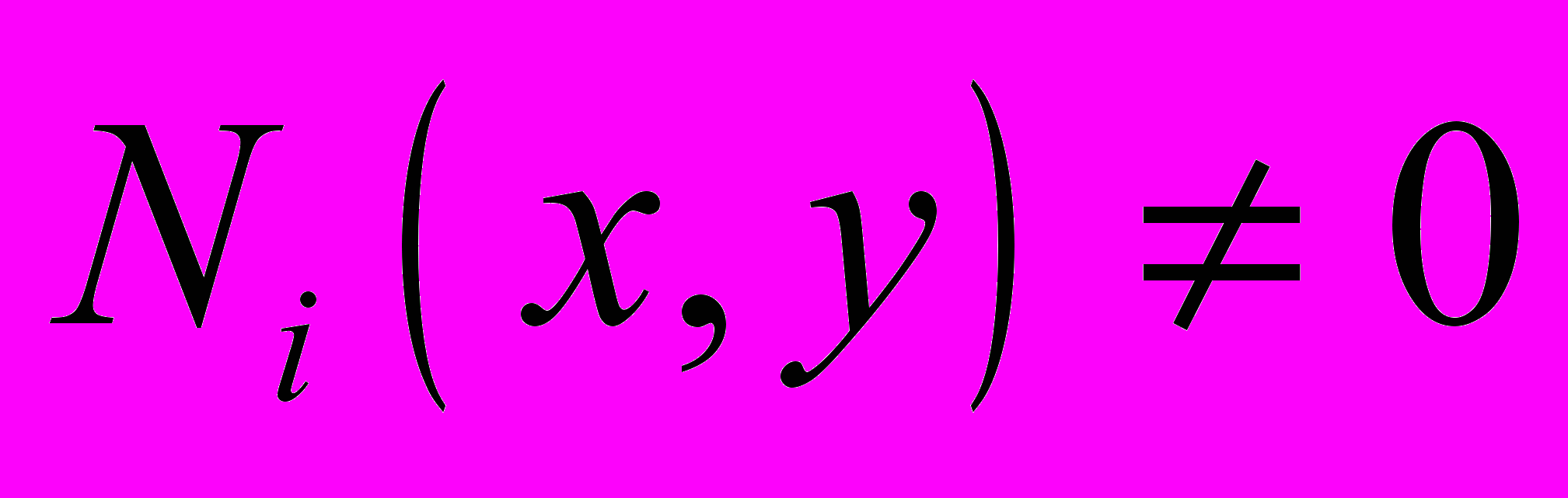в произвольной точке отрезка 
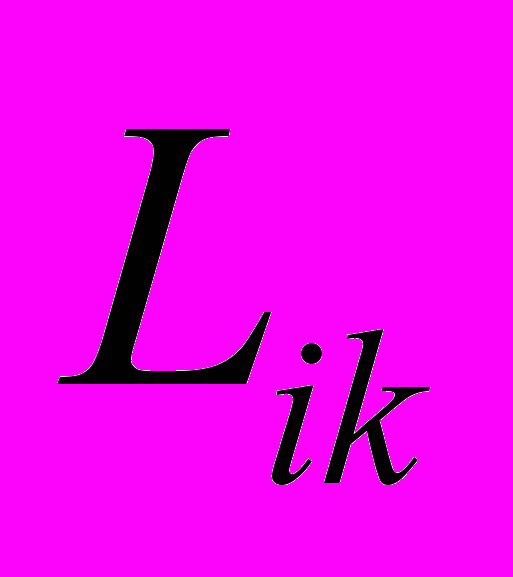. Задайте координаты узлов: Xi=1, Yi=2; Xj=2, Yj=1; Xk=3, Yk=3. Найдите значения этой функции, изменяя значения x в пределах от Xi до Xk , и постройте ее график.4.4 Покажите, что базисные функции 4-го элемента базового каталога удовлетворяет критерию (4.5.2).
4.5 Методом Лагранжа найдите базисные функции радиальных двумерных треугольника и четырехугольника, лежащих в основании 4-го и 5-го элементов каталога.
4.6 Методом Лагранжа найдите базисные функции элементов, порождающих элементы каталога с номерами 8-10.
4.7 Найдите трансляцией базисные функции 5-го элемента базового каталога.
4.8 Найдите базисные функции для элементов
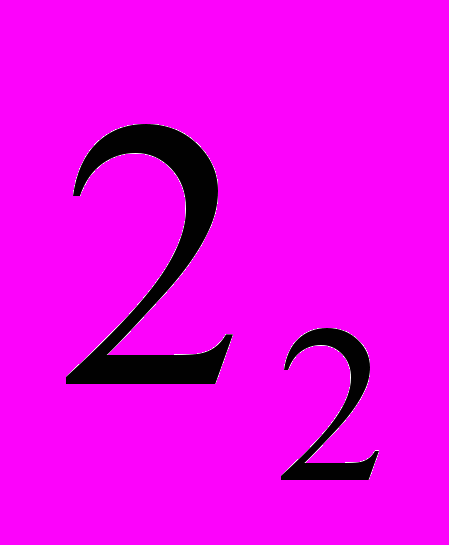или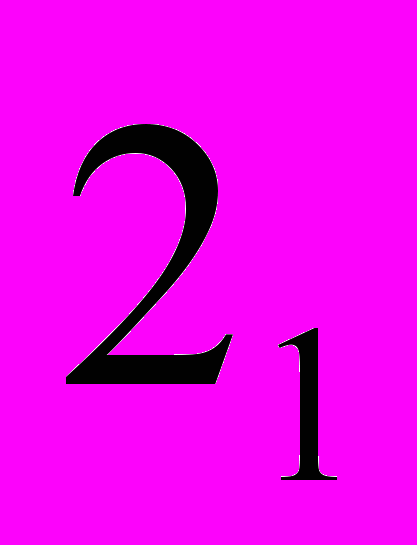 
каталога. Проверьте результат по критерию (4.5.2).4.9 Возможна ли дискретизация 2-мерной области треугольными элементами разного порядка?
Задание 5
5.1 Получите базисные функции всех элементов каталога.
5.2 Получите стандартизованные матрицы теплопроводности второго, третьего и шестого элементов каталога, используя
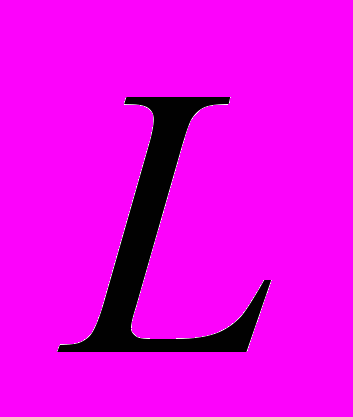-координаты.5.3 Найдите среднеповерхностные температуры одного из элементов каталога.
Задание 6
6.1 Получите решение системы дифференциальных уравнений (6.2.1) методом Галеркина, используя версию МКЭ, аппроксимирующую функцию на k-ом временнόм шаге.
6.2 Почему при определении по (6.4.7) разности
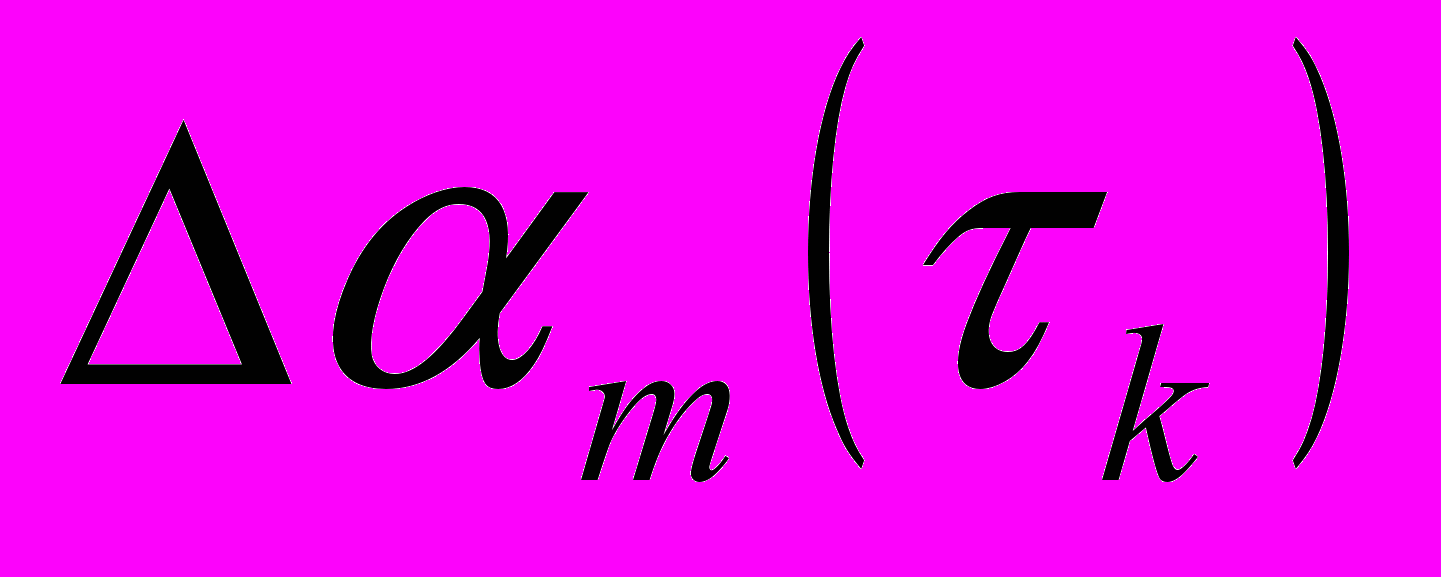нужно привлекать значения 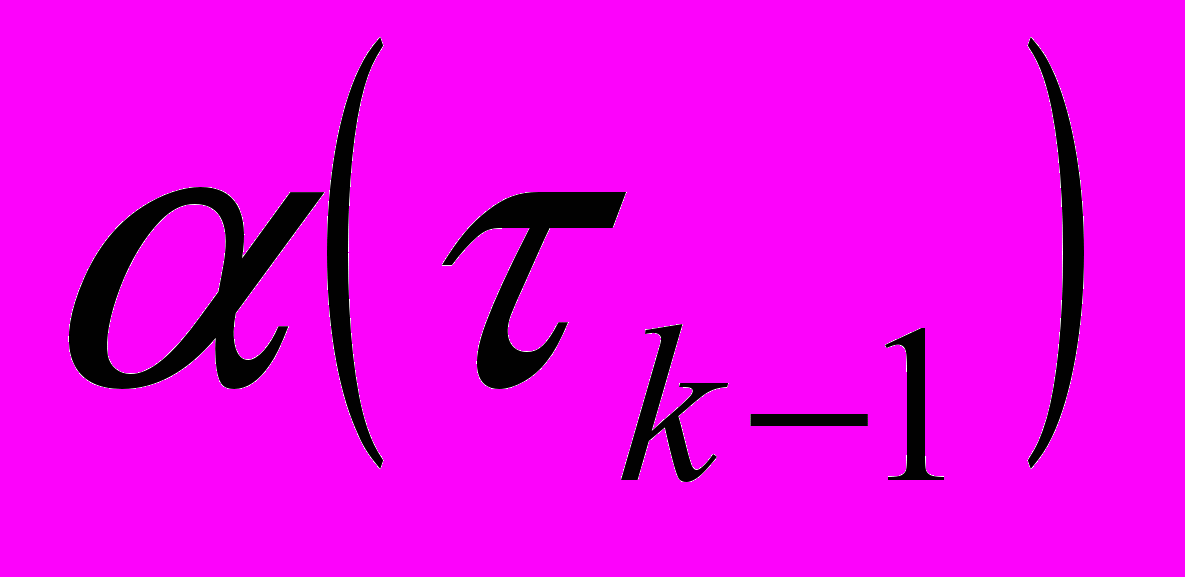и 
и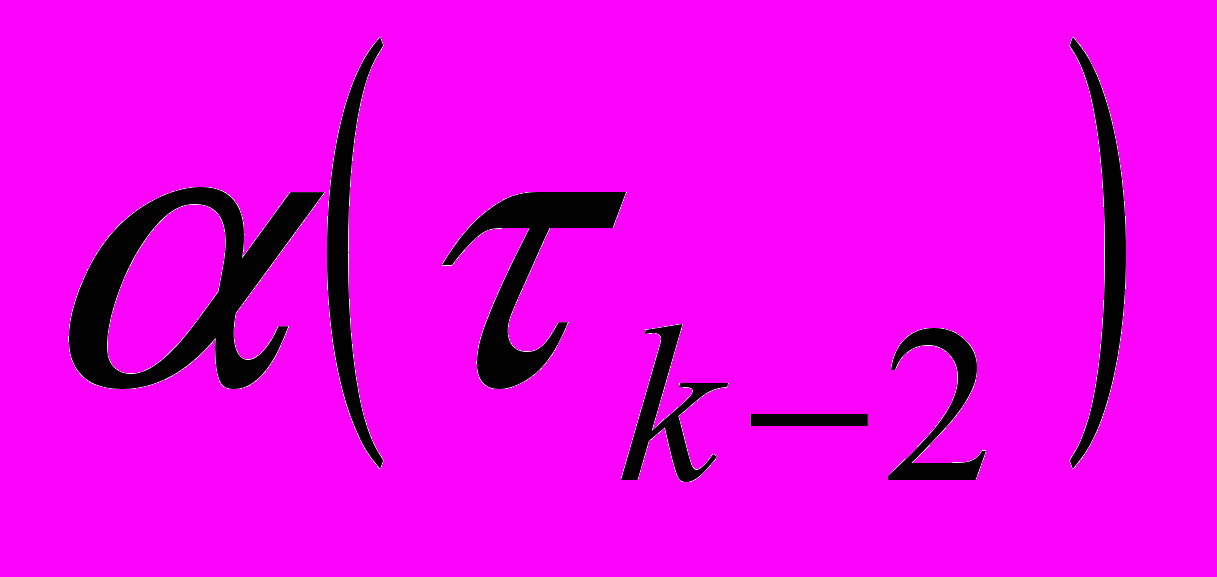 
, т.е. на предыдущих двух, а не на одном временном шаге?6.3 Как изменится динамическое уравнение для элемента, если радиационный компонент представить в граничных условиях выражением
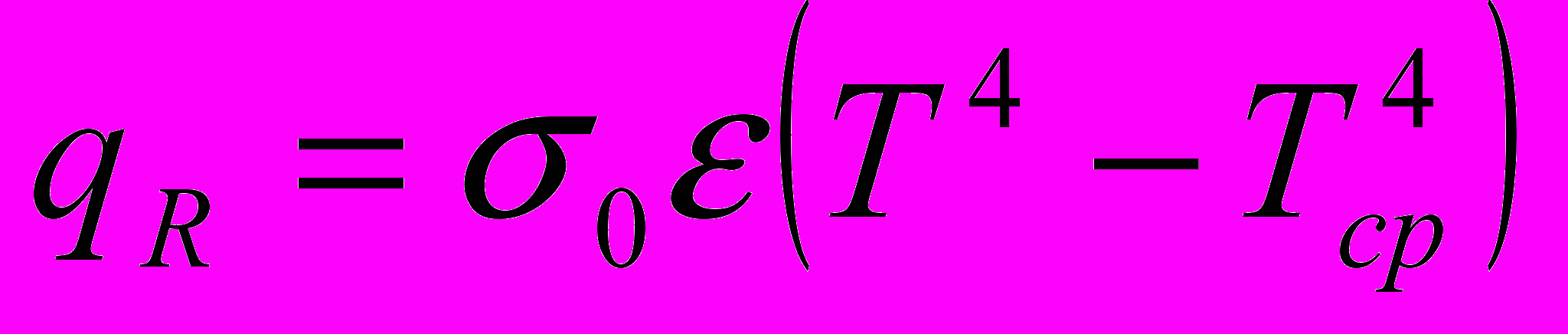, а не в виде числа, определяемого на предыдущем шаге, согласно (6.5.1)? Какие трудности программного и математического характера должны при этом возникнуть?6.4 Возможны ли случаи, когда радиационный компонент можно не учитывать?
Перечень вопросов на итоговую аттестацию (зачет)
1. Основная концепция и преимущества метода конечных элементов.
2. Получите уравнение теплопроводности в обобщенной криволинейной системе
координат.
3. Обобщенное решение краевой задачи методом Галеркина для элементного вклада
4. Геометрические аспекты МКЭ, формирование геометрической части таблицы
входных данных.
5. Получение базисных функций для элемента из базисного каталога элементов.
6. Методы нахождения базисных функций. Их свойства как критерии правильнос-
ти их нахождения.
7. Матричное представление элементного вклада.
8. Формирование глобальных матриц из сокращенных матриц элементов.
9. Найдите выражения для стандартизованных матриц элемента в различных системах коор-
динат.
10. Получите расчетные формулы для средних объемной и поверхностных темпера-
тур одного из элементов базового каталога по их узловым значениям.
11. Решение системы динамических уравнений в рамках МКЭ.
Аннотация
Курс предназначен для ознакомления студентов с наиболее эффективным численным методом расчета сложного теплообмена в системах различного назначения. По освоении курса студент должен иметь четкие представления об алгоритме использования МКЭ для решения задачи, навыки практического пользования программами расчета, базирующихся на МКЭ.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная литература:
По методу конечных элементов
1. Румянцев А.В. Метод конечных элементов в задачах теплопроводности: Учеб. пособ. Калининград.: Изд-во КГУ.1-е изд-е – 1995, 170 с.; 2-е изд-е – 1997, 99 с.
2. Сегерлинд Л. Дж. Применение метода конечных элементов. М.: Мир, 1979.
3. Норри Д., Фриз Ж. деФриз. .Введение в метод конечных элементов. М.: Мир, 1981.
4. Зенкевич О., Чанг И., Метод конечных элементов в теории сооружений и в механике сплошных сред. М.: Недра, 1974.
5. Коннор Дж., Бреббиа К. Метод конечных элементов в механике жидкости. М.: Судостроение, 1979.
6. Оден Дж. Конечные элементы в механике сплошных сред. М.:
Мир, 1976, 464 с.
7. Силвестр П., Феррари Р. Метод конечных элементов для радиоинженеров и инженеров-электриков. М.: Мир, 1986.
8. Кандидов В.П., Чесноков С.С., Выслоух В.А. Метод конечных элементов в задачах динамики. М.: Изд-во МГУ, 1980.
9. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения: Учеб. пособ, М.: Наука, 1985, 231 с.
10. Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. М.: Нау- ка, 1965, 426 с.
11. Пытьев Ю.П., Васильева А.Б., Пытьева Г.П. Аналитическая геометрия с элементами линейной алгебры: Учеб. пособ. М.: Изд-во Моск. ун-та, 1986, 140 с.
12. Волков Е.А. Численные методы. М.: Наука, 1982, 254 с.
13. Марчук Г.И. Методы вычислительной математики. М.: Наука, 1977, 536 с.
14. РумянцевА.В., Васильев В.В. Решение нестационарной осесимметричной задачи теплопроводности методом конечных элементов с использованием комплекс-элемента. Деп. ВИНИТИ, № 123-В94.
15.Румянцев А.В. Температура теплоносителя в длинном неизотермическом канале. Деп. ВИНИТИ, № 2679-В95.
16. Румянцев А.В., Сергеенкова Р.С., Васильев В.В. Решение нестационарной осесимметричной задачи теплопроводности методом конечных элементов с учетом радиационного теплообмена. Деп. ВИНИТИ, № 125-В94.
17. Румянцев А.В., Агапитов Д.А., Остроух А.Н., Хоменко А.В. Система угловых коэффициентов излучения коническо-цилиндрической камеры с торцами. Деп. ВИНИТИ,
№ 1963-В94.
18. Румянцев А.В., Хоменко А.В., Васильев В.В. Система угловых коэффициентов излучения коаксиальной камеры с кольцевыми торцами. Деп. ВИНИТИ, № 1654-В95.
По основам теплообмена и тепловому проектированию
19. Основы теплопередачи в авиационной и ракетно-космической технике: Учебник для авиационных специальностей вузов./ Авдуевский В.С., Галицейский Б.М., Глебов Г.А. и др. М.: Машиностроение, 1992, 582 с.
20. Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967, 599 с.
21. Арнольд П.В., Михайловский Г.А., Селиверстов В.Н. Техническая термодинамика и теплопередача. М.: Высшая школа, 1979, 444 с.
22. Юдаев Б.Н. Техническая термодинамика: Теплопередача. М.: Высшая школа, 1988, 479 с.
23.Исаченко В.П., Осипов В.А., Сукомел А.С.Теплопередача. М.: Энергия, 1975, 424 с.
24. Зарубин B.C. Инженерные методы решения задач теплопроводности. М.: Энергоатомиздат, 1983, 328 с.
25. Темкин А.Г. Обратные методы теплопроводности. М.: Энергия, 1973, 464 с.
26.Лыков А.В. Тепломассообмен. Справочник. М.: Энергия, 1978, 480 с.
27.Дрейцер Г.А. Конвективный теплообмен в каналах: Учеб.пособ. М.: Изд-во МАИ, 1984, 77 с.
28. Мартыненко О.Г., Соковишин Ю.А. Свободно-конвективный теплообмен: Справочник. Минск: Наука и техника, 1982, 400 с.
29. Себеси Г., Брэдшоу П. Конвективный теплообмен. Физические основы и вычислительные методы. М.: Мир, 1987, 592 с.
30. Зигель Р., Хауэлл Д. Теплообмен излучением. И.: Мир, 1975, 934 с.
31.Зарубин B.C. Температурные поля в конструкции летательных аппаратов. М.: Машиностроение, 1978, 184 с.
32.Залетаев В.М., Капинос Ю.В., Сургучев О.В. Расчет теплообмена космического аппарата.М.Машиностроение,1979, 208 с.
33.Галицейский Б.Н. Теплопередача в авиационных двигателях. М.:Изд-в МАИ,1985, 82 с.
34.Алемасов В.Е. Теория ракетных двигателей .М.: Оборонгиз, 1965.
35. Теплообмен в энергетических установках космических аппаратов. Галицейский Б.М., Данилов Ю.И., Дрейцер Г.А., Кошкин В.К. М.: Машиностроение, 1975, 272 с.
36. Полежаев Ю.В., Юревич Ф.Б. Тепловая защита. М.: Энергия, 1976, 392 с.
37. Селин В.В. Теплотехника на рыбообрабатывающих предприятиях и промысловых судах. М.: Легк. и пищ. промыш., 1982, 264 с. Тепловой расчет котельных агрегатов (норма-
тивный метод). М.: Энергия, 1973, 296 с.
38. Вульман Ф.А., Хорьков Н.С Тепловые расчеты на ЭВМ теплотехнических установок. М.: Энергия, 1975, 198 с.
39. Маргулова Т.Атомные электрические станции.М.: Высшая школа,1978,311 с.
40. Алифанов О.М. Идентификация процессов теплообмена летательного аппарата. М.: Машиностроение, 1979, 216 с.
41.Попырин Л.С. Математическое моделирование и оптимизация теплоэнергетических установок. М: Энергия, 1978, 415 с.
42. Вигак В.М. Оптимальное управление нестационарными тепловыми режимами. Киев.: Наукова думка, 1979, 359 с.
43.Лаврентьев М.Н., Романов В.Г., Шишатский С.П. Некорректные задачи математической физики и анализа. М.: Наука, 1980, 288 с.
44. Коздоба Л.А. Вычислительная теплофизика.Киев.:Наукова думка,1992, 276 с.
45. Панкратов Б.М. Основы теплового проектирования транспортных космических систем. М.: Машиностроение, 1988, 303 с.
46. Моделирование тепловых режимов космического аппарата и окружающей его среды. Под ред. акад. Петрова Г.И. М.: Машиностроение, 1971, 380 с.
47.Конструкция и проектирование космического летательного аппарата. М.: Машиностроение, 1986, 344 с.
48. Гущин В.В., Панкратов Б.Н., Родионов А.Д. Основы устройства и конструирования космических аппаратов. М.: Машиностроение, 1992, 278 с.
49. Малоземов В.В. Выбор проектных параметров подсистем терморегулирования. М.: Изд-во МАИ, 1986, 344 с.
50. Малоземов В.В., Логинов С.Н., Мартиросова Е.И. Математическое моделирование элементов, агрегатов, систем обеспечения теплового режима летательных аппаратов. М.: Изд-во МАИ, 1986, 91 с.
51. Малоземов В.В., Логинов С.Н., Кутепов С.Н. Анализ и исследование подсистем обеспечения теплового режима летательных аппаратов. М.: Изд-во МАИ, 1987, 103 с.
52. Андрейчук О.Б., Малахов Н.Н. Тепловые испытания космического аппарата. М.: Машиностроение, 1982, 143 с.