Geum.ru

Методические указания и контрольные задания по физике для слушателей второго курса фзо москва 2004

Вид материалаМетодические указания
Условие нормировки вероятностей
Уравнение Шредингера для стационарных состояний
A – амплитуда колебаний волн де Бройля; p
Собственная энергия электрона водородоподобного атома
Энергия ионизации атома водорода
Подобный материал:
1   ...   10   11   12   13   14   15   16   17   18

Условие нормировки вероятностей:




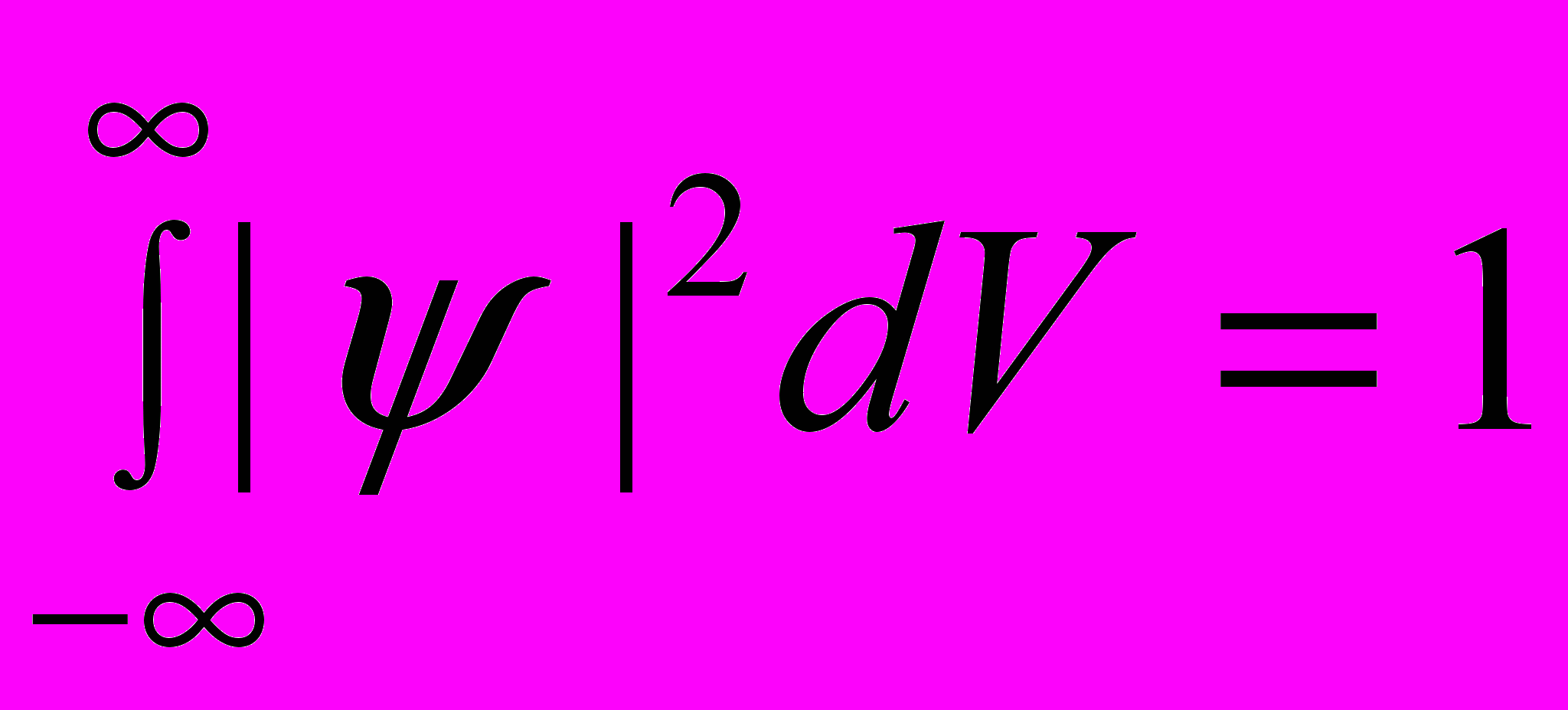
Волновая функция ψ, являясь основной характеристикой состояния микрообъектов, должна быть конечной (вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями ψ1, ψ2, … ψп, …, то она также может находиться в состоянии ψ, описываемом линейной комбинацией этих функций:



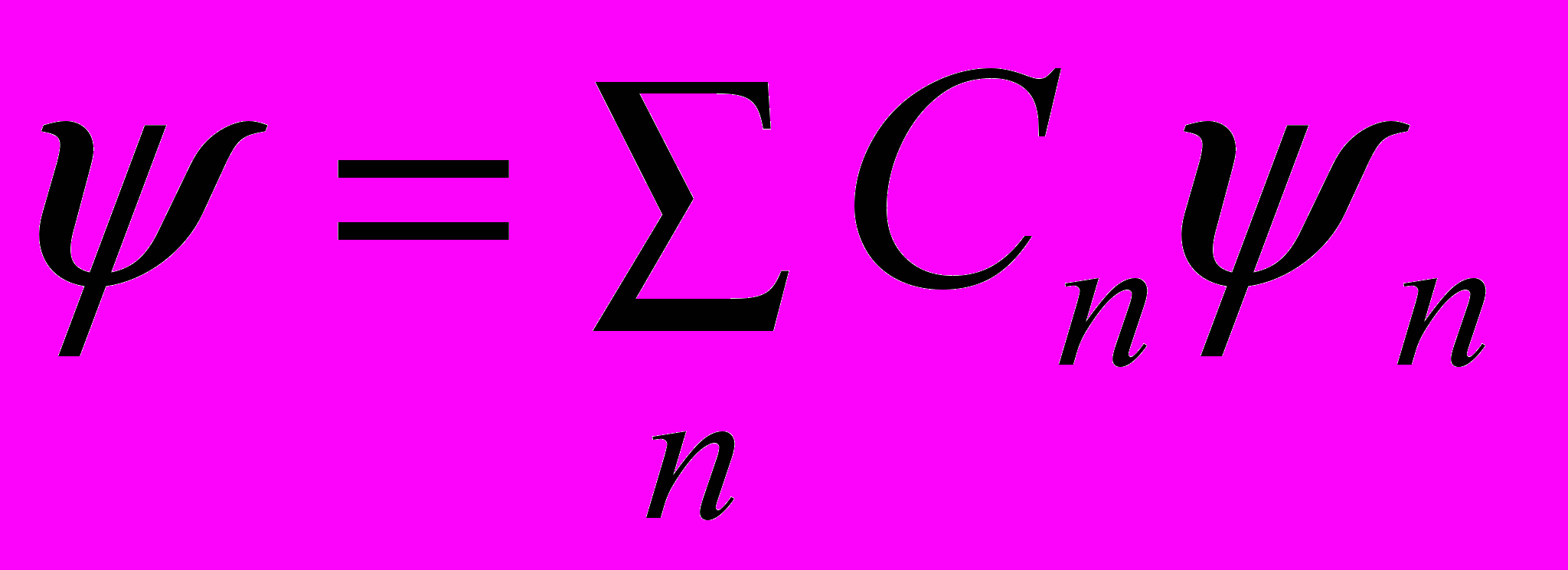
где Cп (п = 1,2, …) – произвольные, вообще говоря, комплексные числа.

Вероятность обнаружения частицы в интервале от х1 до х2:



Среднее значение физической величины L, характеризующей частицу, находящуюся в состоянии, описываемом волновой функцией ψ:




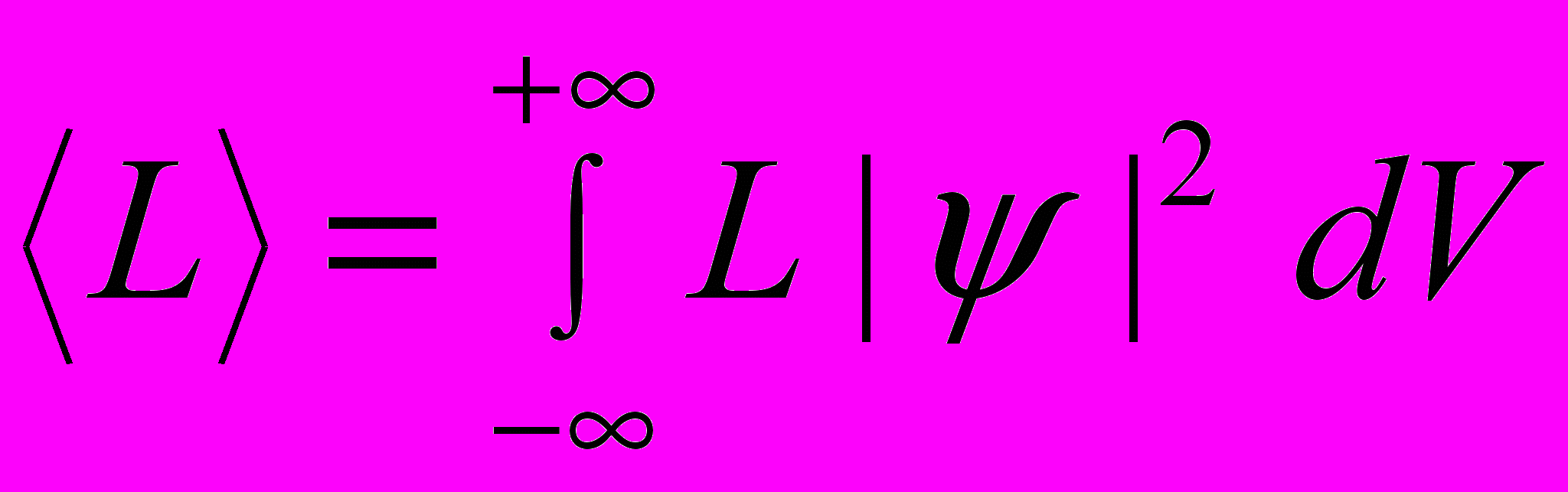
Общее уравнение Шредингера:



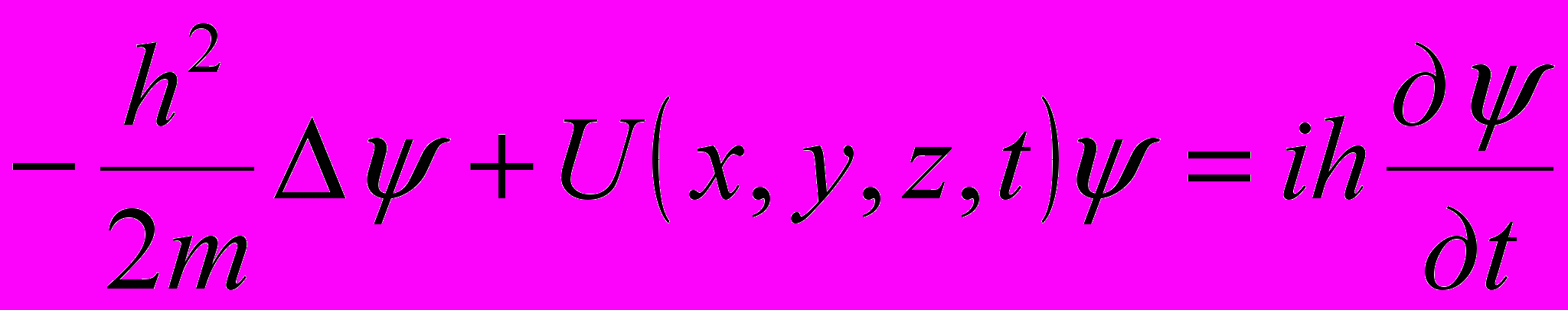
где ψ = ψ (х,у,z,t) – волновая функция, описывающая состояние частицы; h = h /(2π); m – масса частицы; Δ – оператор Лапласа 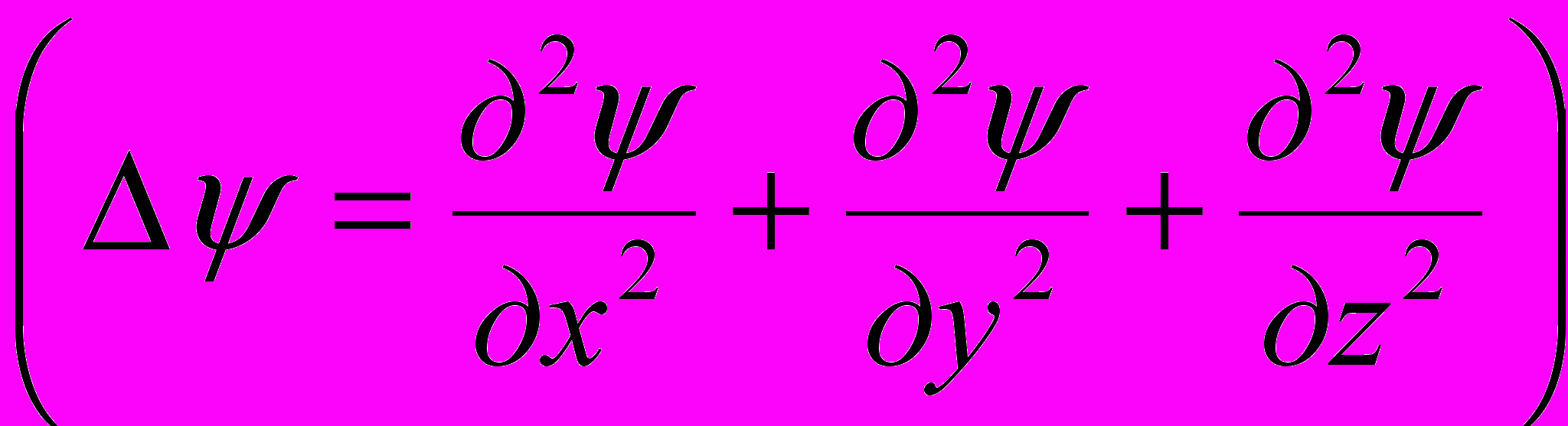; 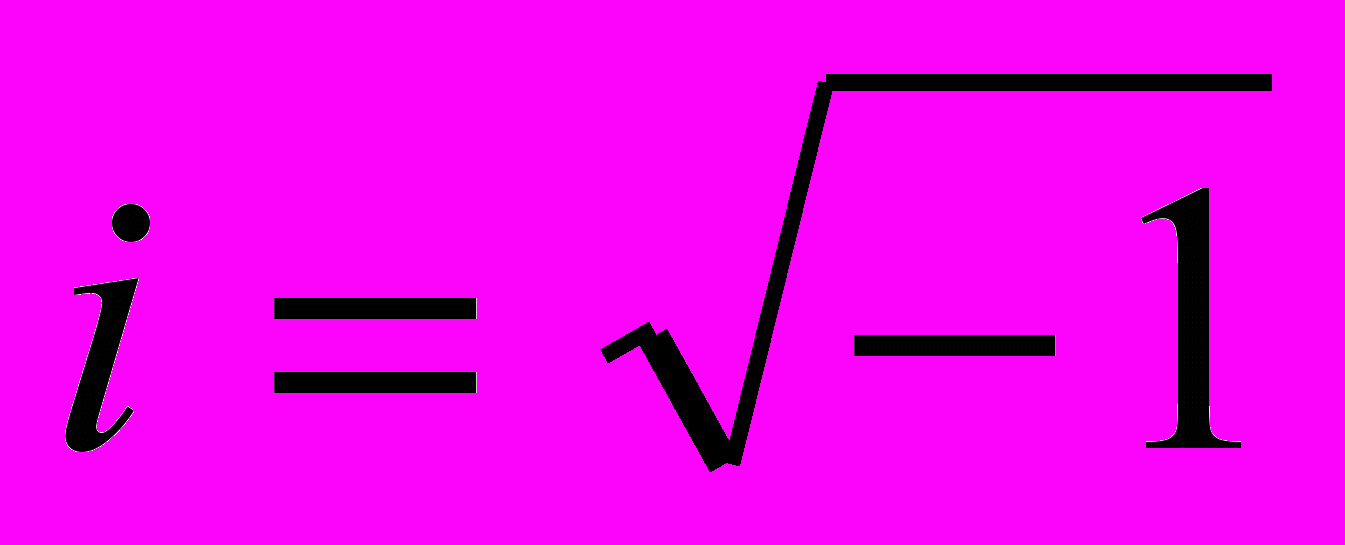- мнимая единица; U = U (х,у,z,t) – силовая функция частицы в поле, в котором она движется.

Уравнение Шредингера для стационарных состояний:




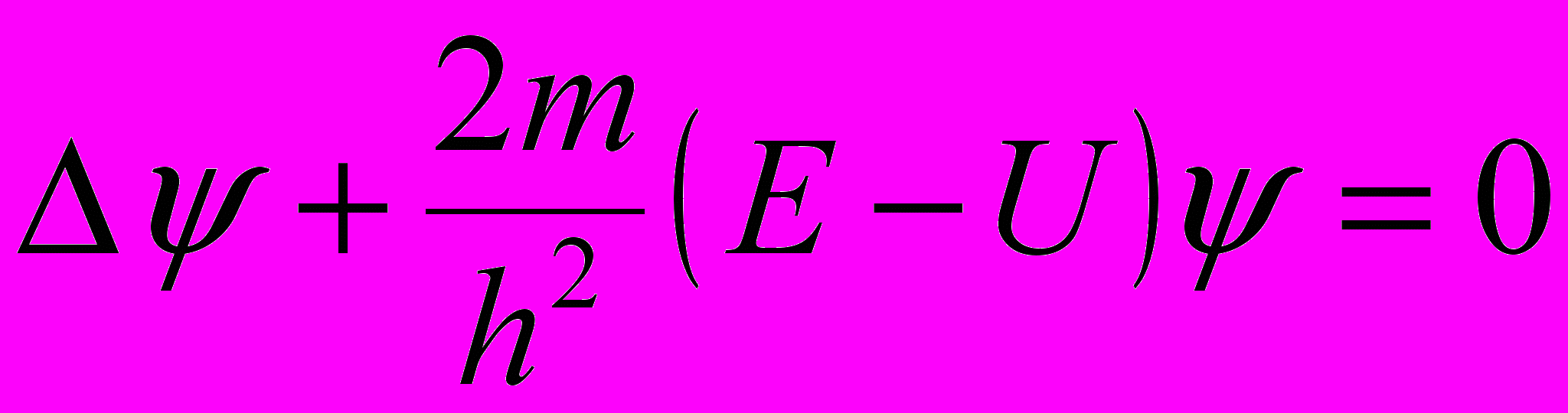
где ψ = ψ (х,у,z) – координатная часть волновой функции (ψ (х,у,z,t) = ψ (х,у,z) е-i(E/h) t); U = U (х,у,z) – потенциальная энергия частицы; Е – полная энергия частицы.

Свободная частица – частица, движущаяся в отсутствие внешних полей.

Волновая функция, описывающая одномерное движение свободной частицы:



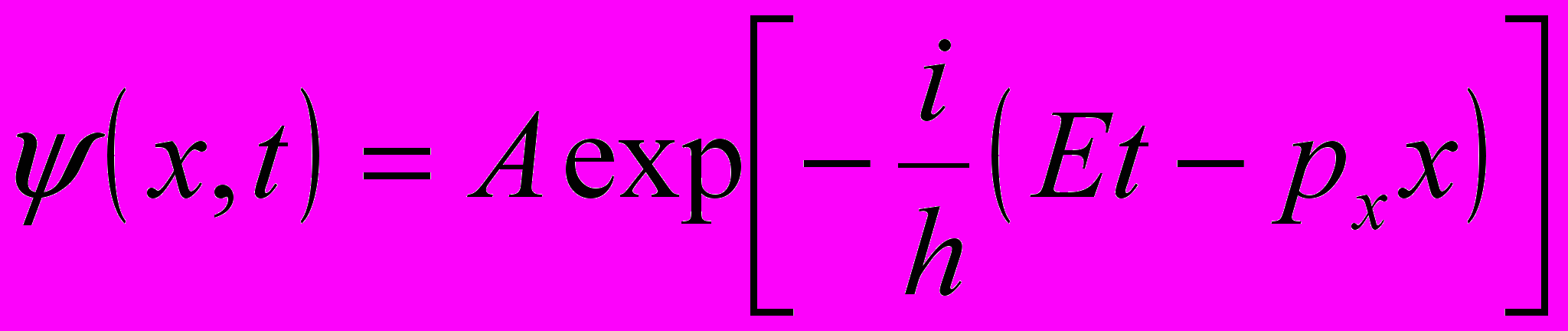
где A – амплитуда колебаний волн де Бройля; px = kh – импульс частицы; E = hω – энергия частицы.

Собственная энергия частицы, находящейся на п-м энергетическом уровне в одномерной прямоугольной “потенциальной яме” с бесконечно высокими “стенками”:



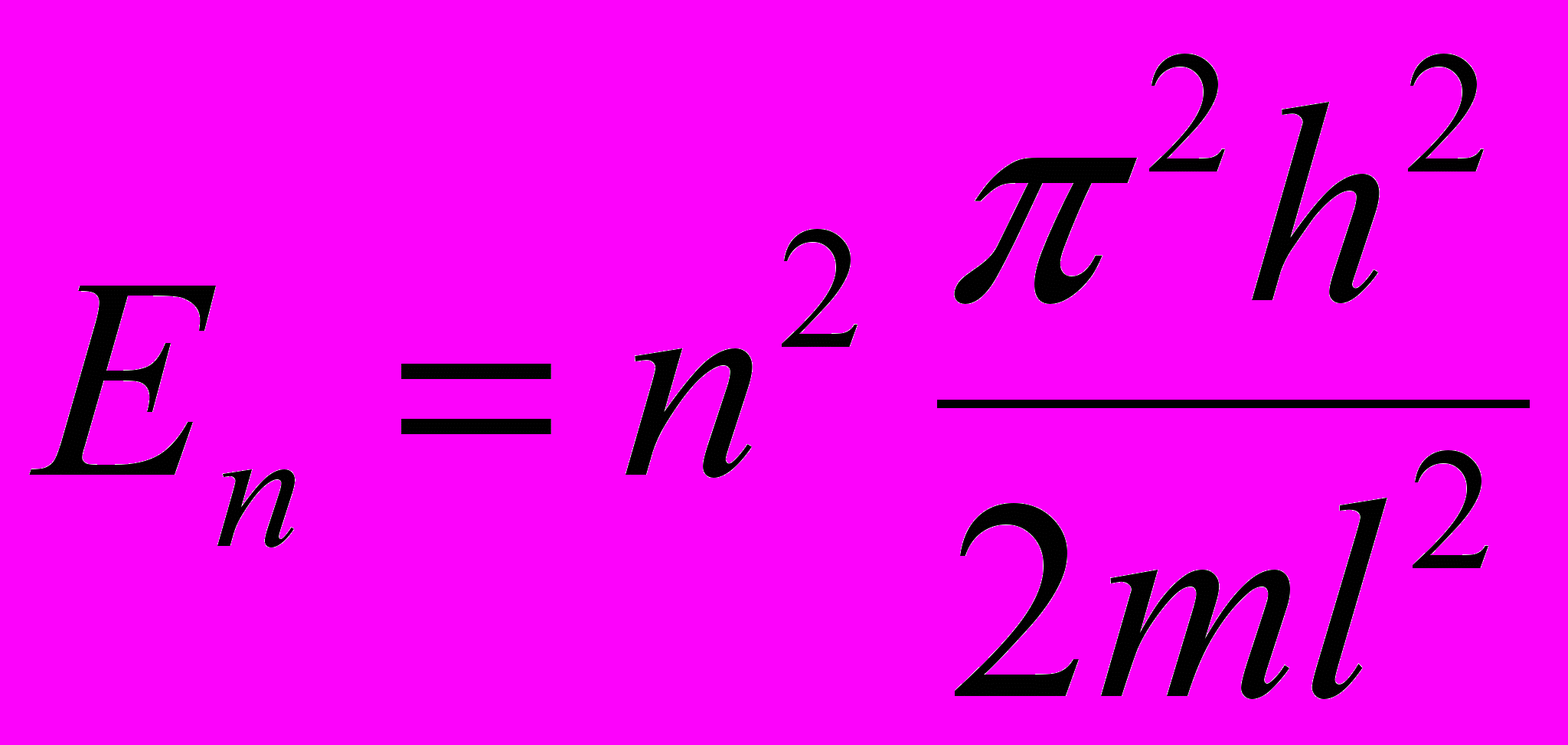
где l – ширина ямы; п = 1,2,3, ….

Энергия Еп принимает лишь определённые дискретные значения, т.е. квантуется.

Уровень энергии – квантованное значение энергии Еп.

Собственная волновая функция, соответствующая собственному значению энергии:



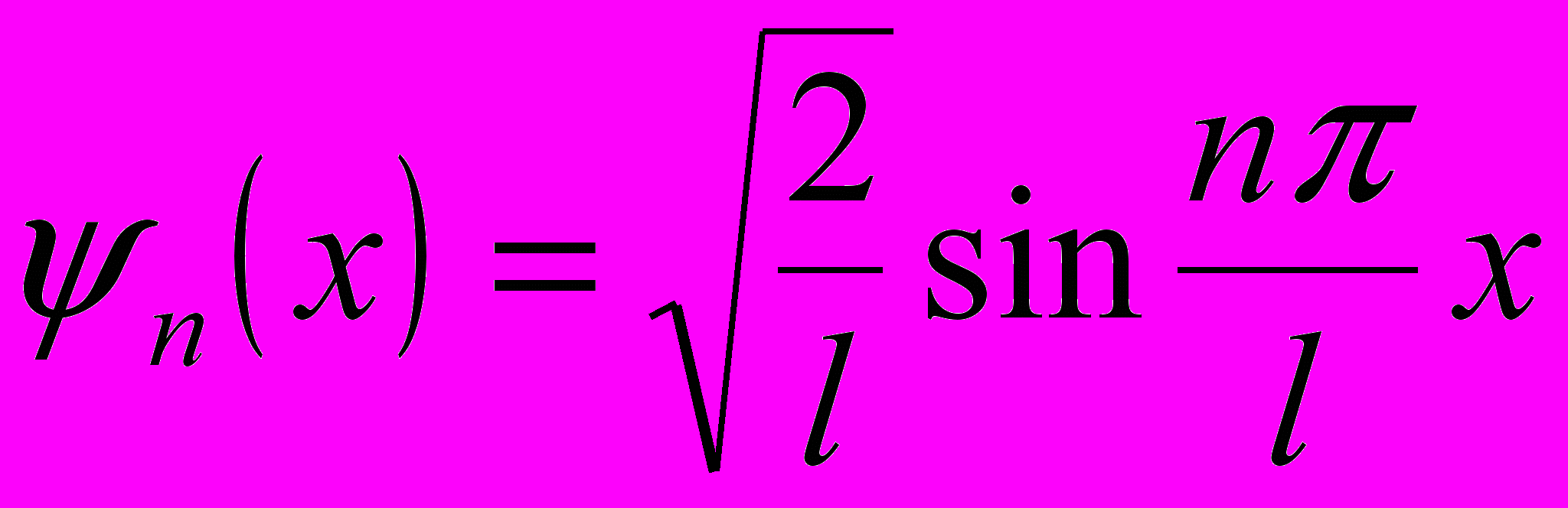
где n = 1,2,3, ….

Потенциальная энергия взаимодействия электрона с ядром в водородоподобном атоме:



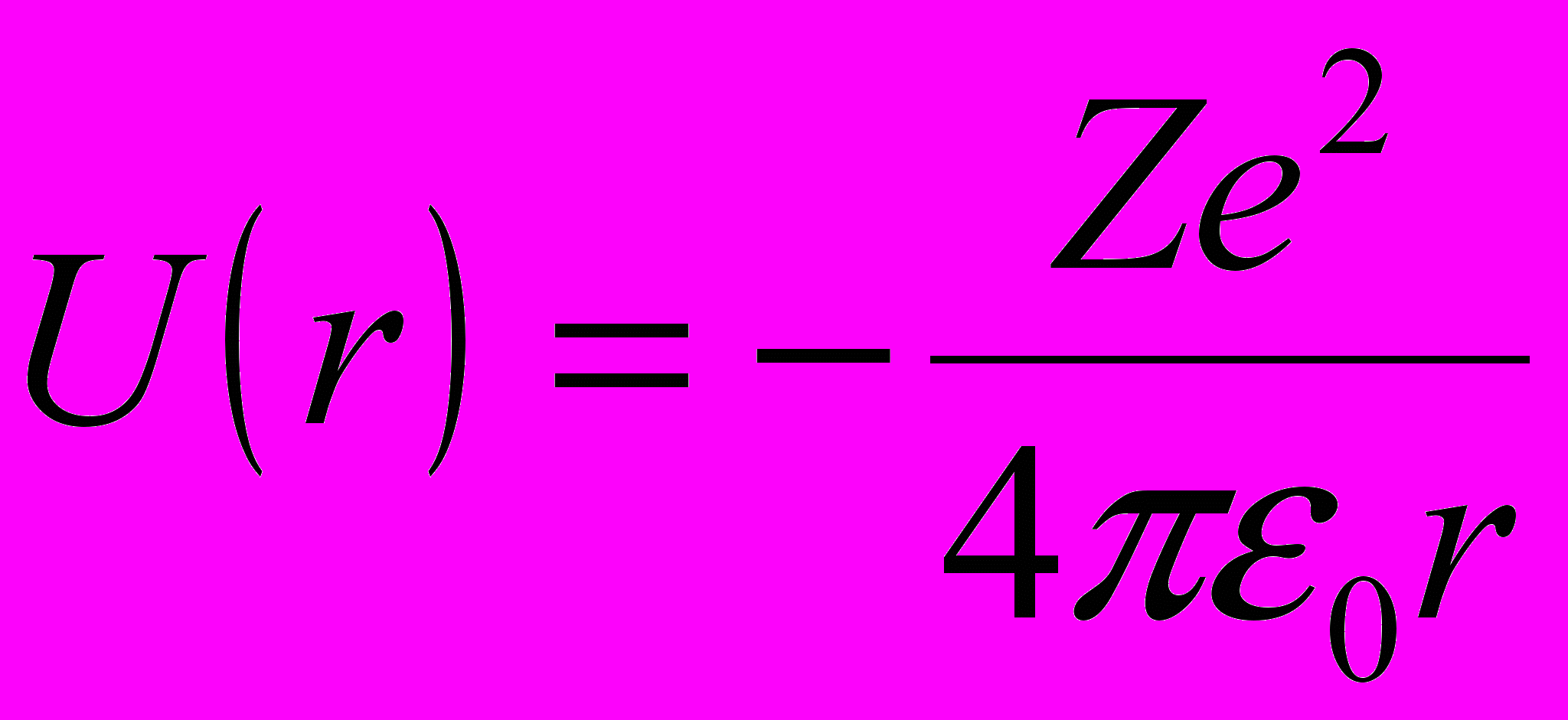
где r – расстояние между электроном и ядром; Z – порядковый номер элемента; ε0 – электрическая постоянная.

Уравнение Шредингера для стационарных состояний электрона водородоподобного атома:



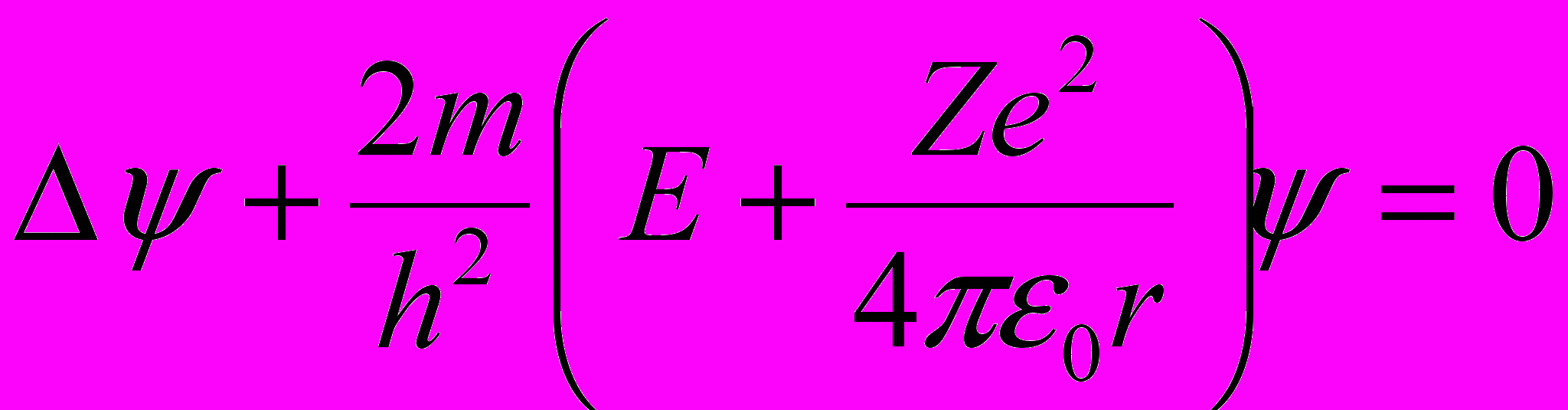
где m – масса электрона; ψ – волновая функция, описывающая состояние электрона; Е – полная энергия электрона в атоме.

Собственная энергия электрона водородоподобного атома:




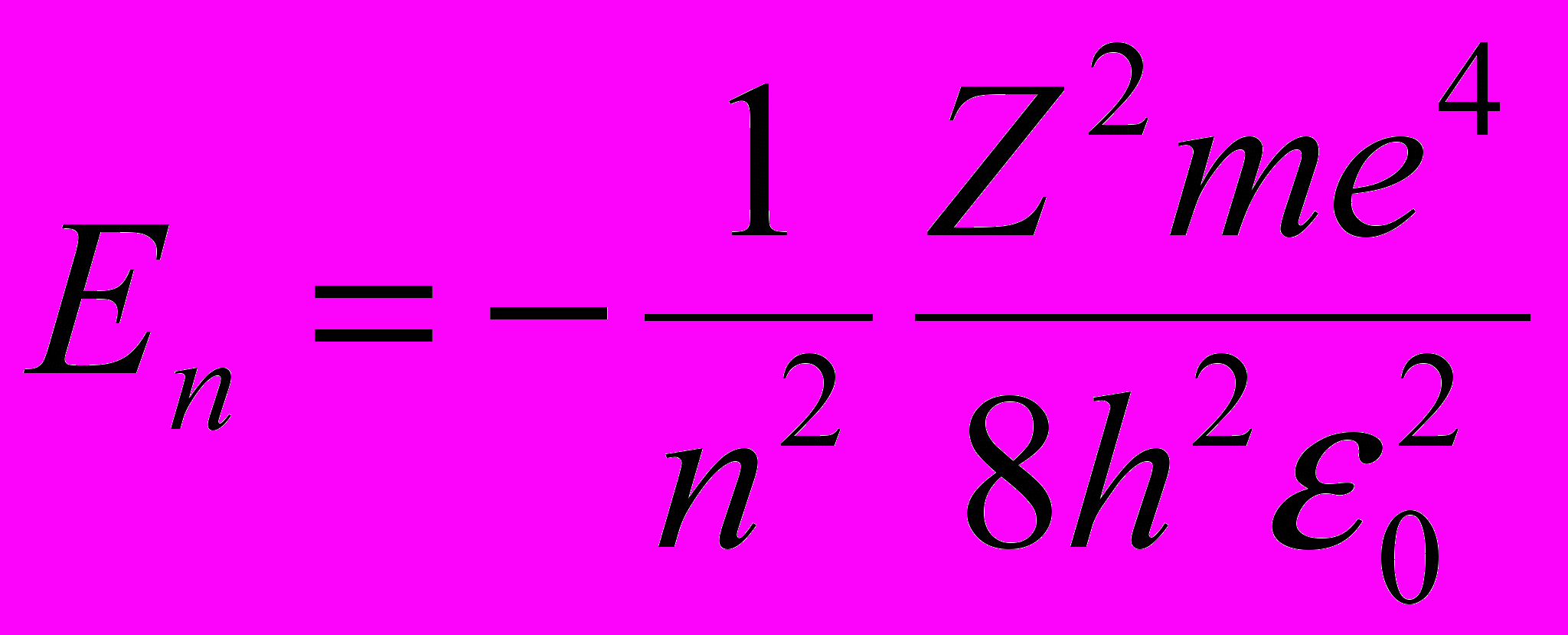
где n = 1,2,3, ….

Главное квантовое число – квантовое число, определяющее энергетические уровни электрона в атоме. Может принимать любые целочисленные значения, начиная с единицы:

п = 1,2,3, …

Энергия ионизации атома водорода:


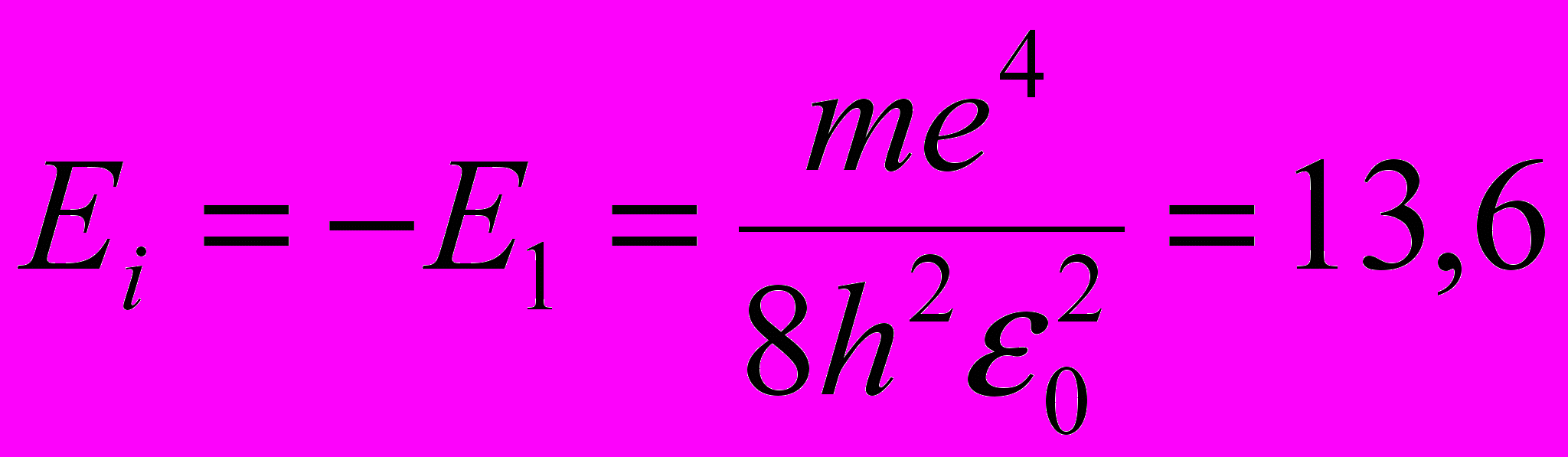эВ

Орбитальное квантовое число – квантовое число, определяющее момент импульса электрона в атоме. При заданном п принимает значения l = 0,1, …, (п – 1), т.е. всего п значений:

l = 0,1, …, п –1

Момент импульса электрона (механический орбитальный момент:



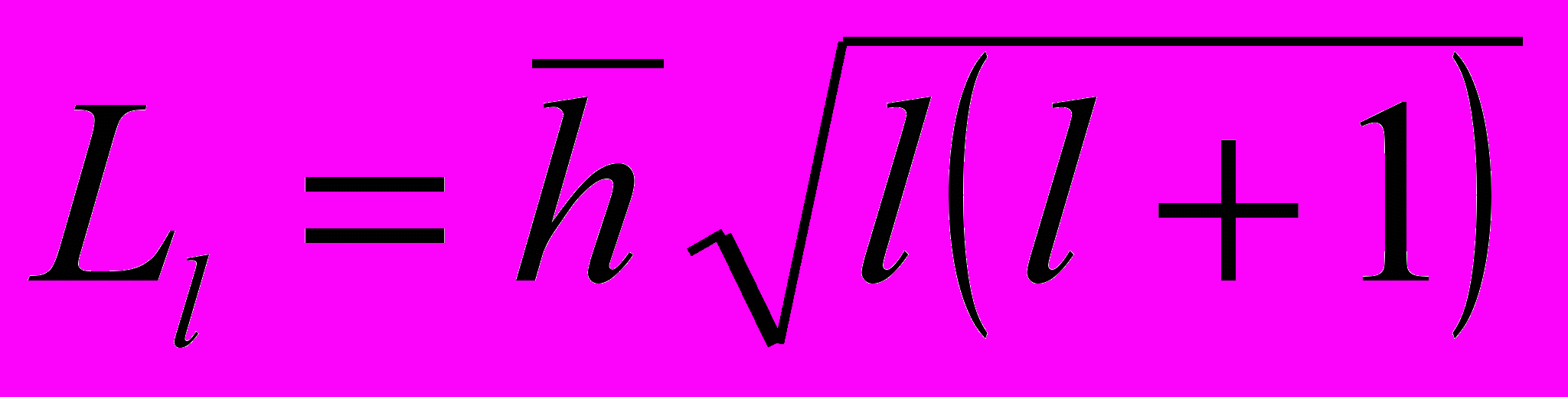
где l – орбитальное квантовое число.

Магнитное квантовое число – квантовое число, определяющее момент импульса электрона на заданное направление. При заданном l принимает значения ml = 0, ±1, ±2, …±l, т.е. всего (2l + 1) значений.

Проекция момента импульса на направление z внешнего магнитного поля:



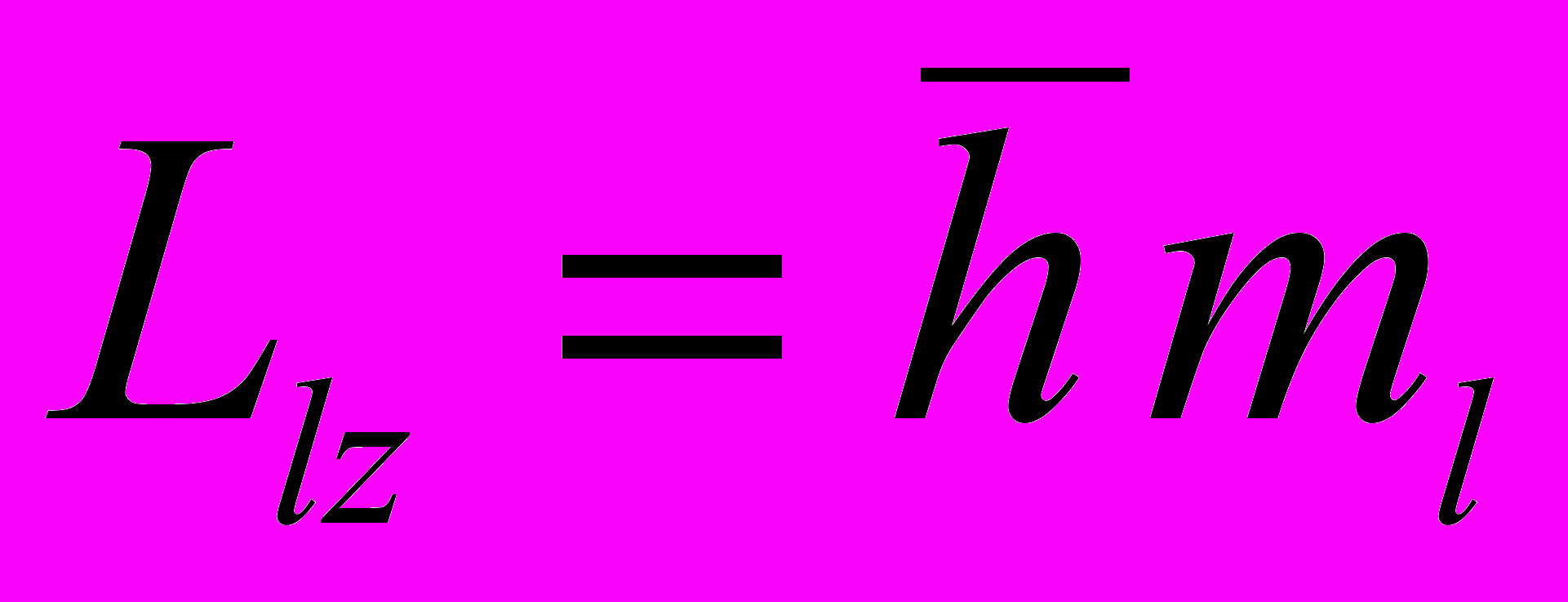
где ml –магнитное квантовое число.