Geum.ru

Методические указания и контрольные задания по физике для слушателей второго курса фзо москва 2004

Вид материалаМетодические указания
Комптоновская длина волны
Постоянная Ридберга
Первый боровский радиус
Z – порядковый номер элемента в системе Менделеева; ε0 – электрическая постоянная; п =
E = hω – энергия частицы (ω
Е – неопределённость энергии данного квантового состояния; Δt
Подобный материал:
1   ...   8   9   10   11   12   13   14   15   ...   18

Комптоновская длина волны:


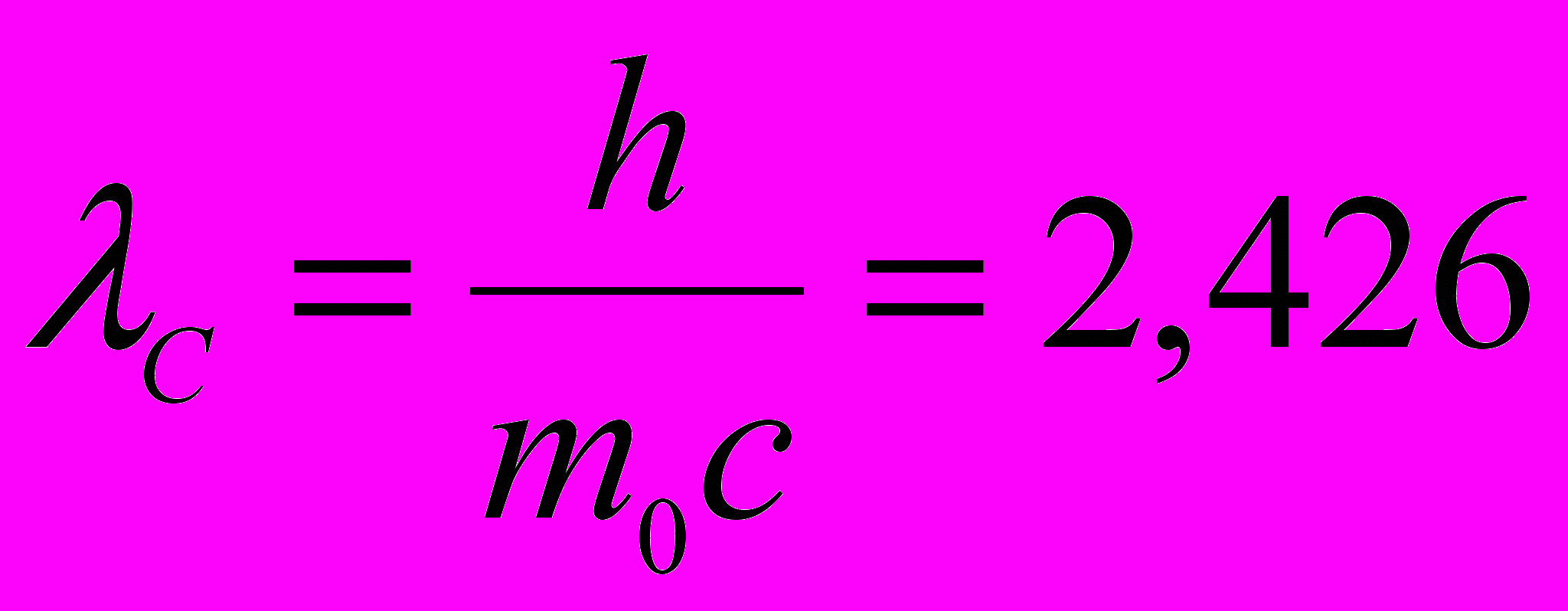пм

Обобщённая формула Бальмера, описывающая серии в спектре атома водорода:



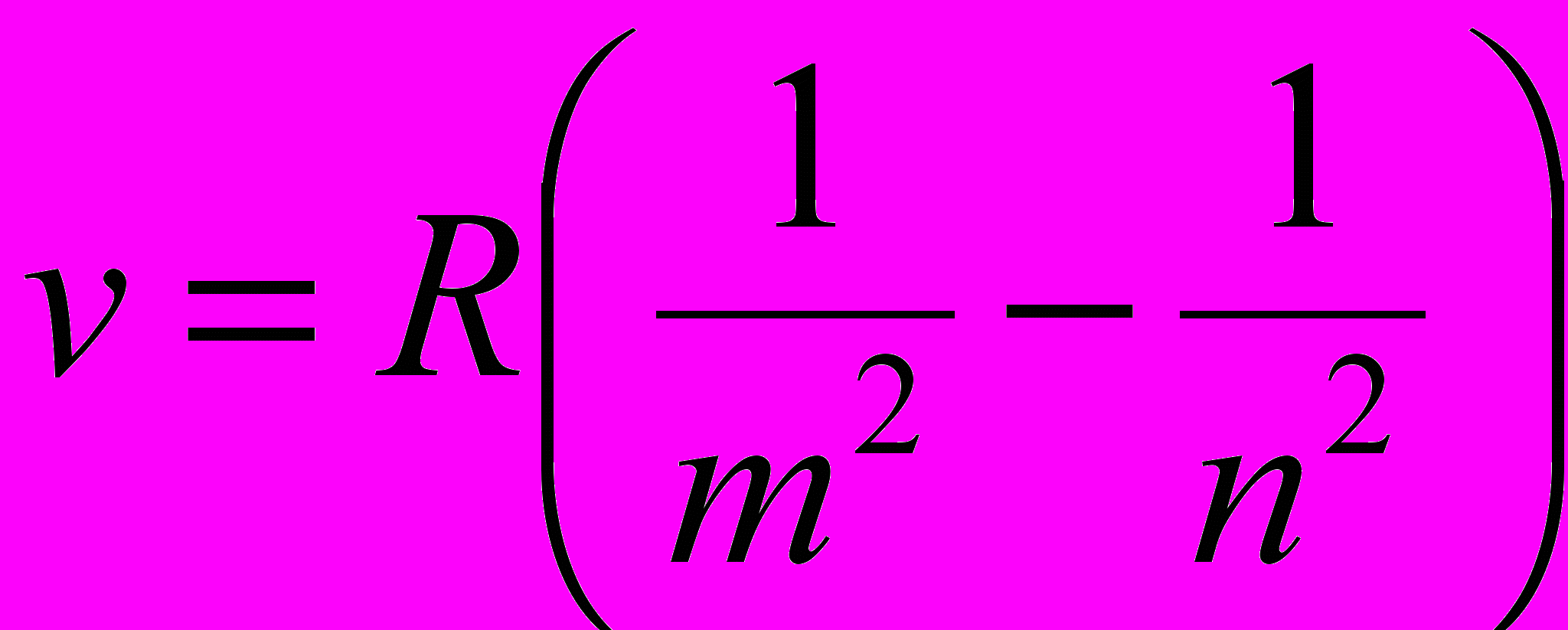
где v – частота спектральных линий в спектре атома водорода; R – постоянная Ридберга; m определяет серию (m = 1,2,3, …); п – определяет отдельные линии соответствующей серии (п = m + 1, m +2, …); m = 1 (серия Лаймана), m = 2 (серия Бальмера), m = 3 (серия Пашена), m = 4 (серия Брэкета), m = 5 (серия Пфунда), m = 6 (серия Хэмфри).

Постоянная Ридберга:


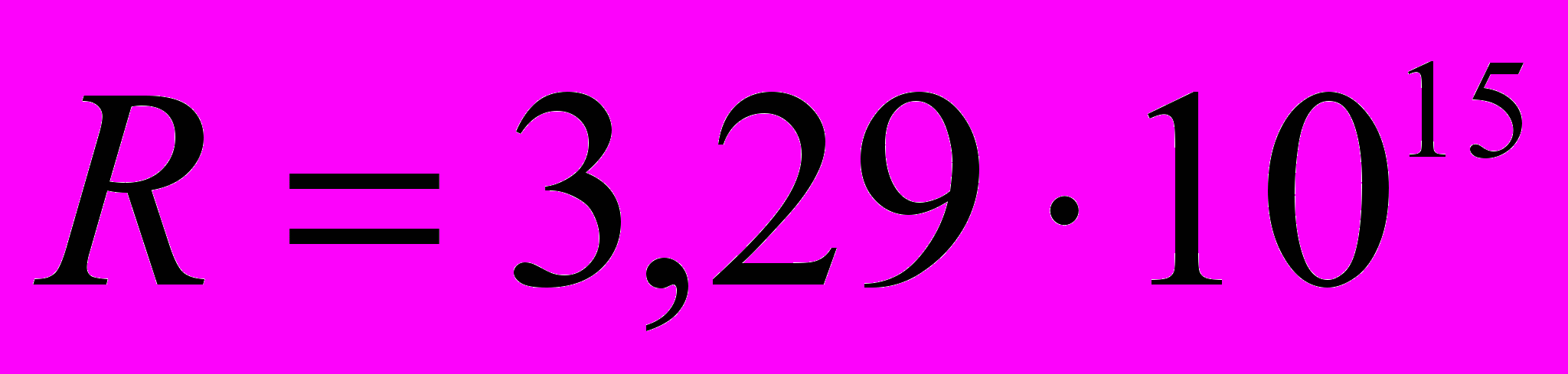с-1

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергию.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, имеет дискретные квантованные значения момента импульса:



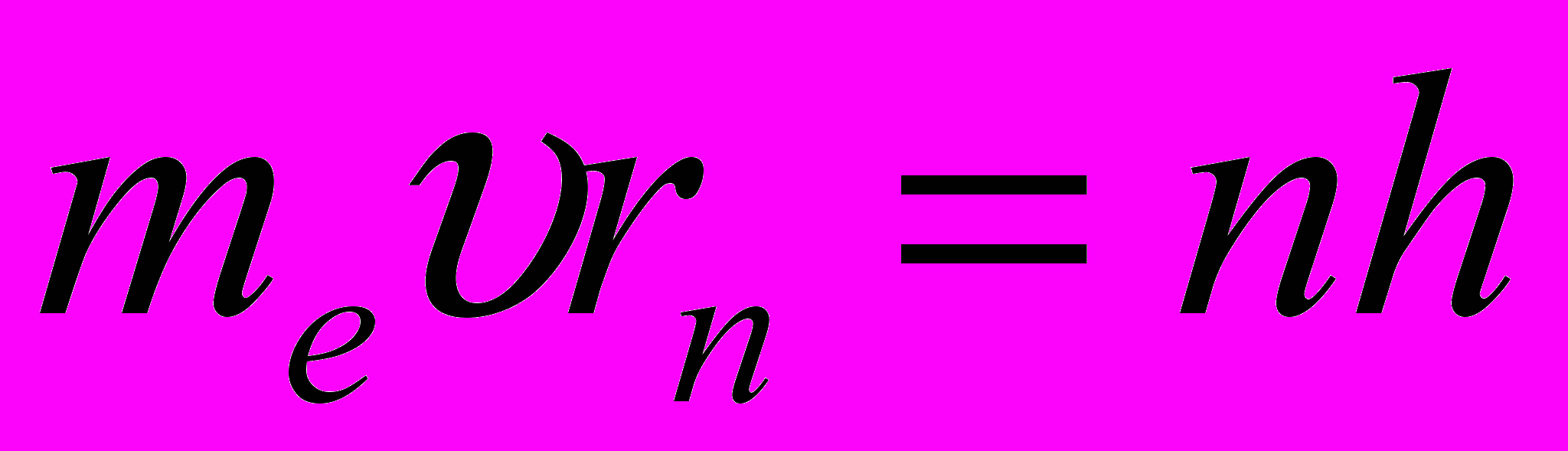
где me – масса электрона, υ – его скорость на п – й орбите радиуса rп, h = h / (2π) (п = 1,2,3, …).

Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией, равной разности энергий соответствующих стационарных состояний:



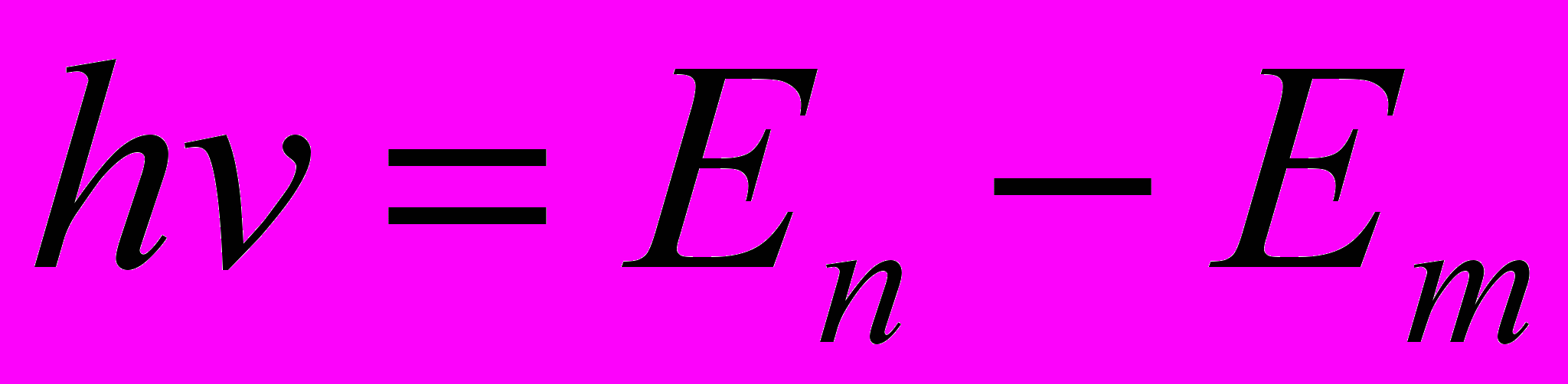
где En и Em – соответственно энергия стационарного состояния атома до и после излучения (поглощения).

Радиус n – й стационарной орбиты:



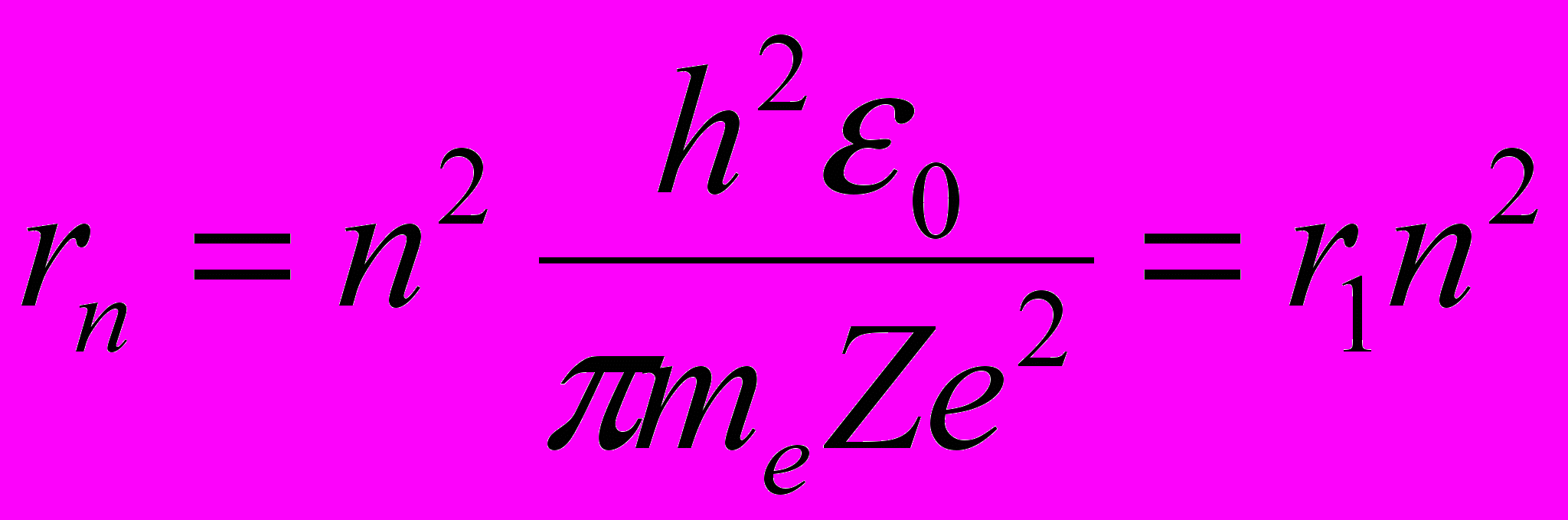
где n = 1,2,3, ….

Первый боровский радиус:


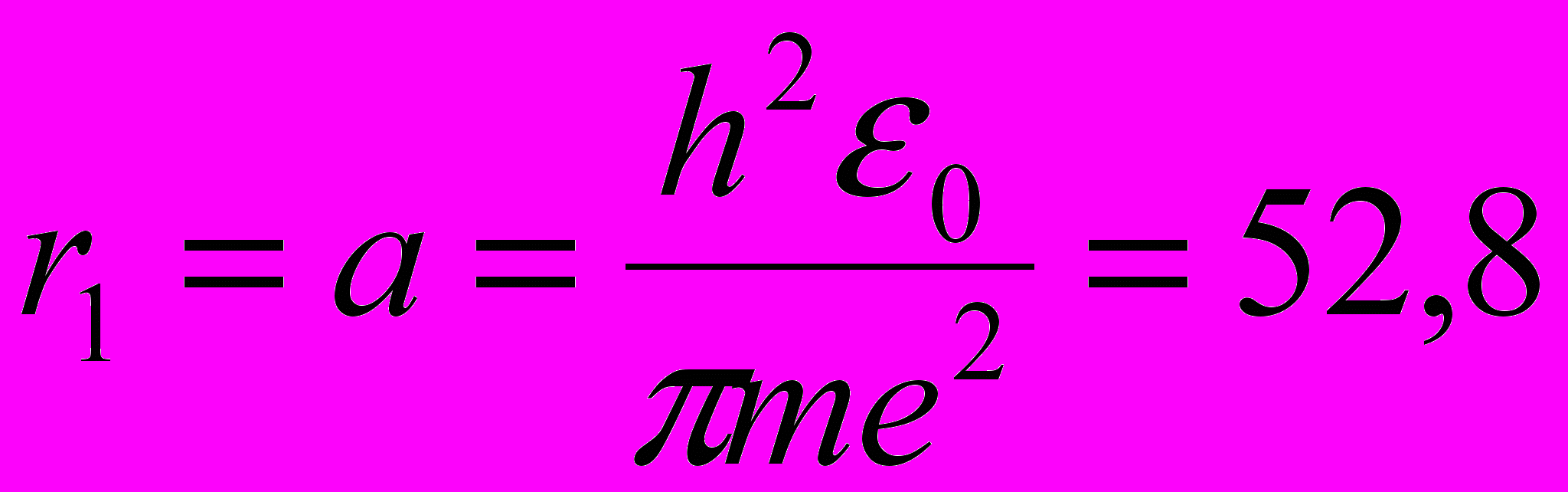пм

Энергия электрона на n – й стационарной орбите:



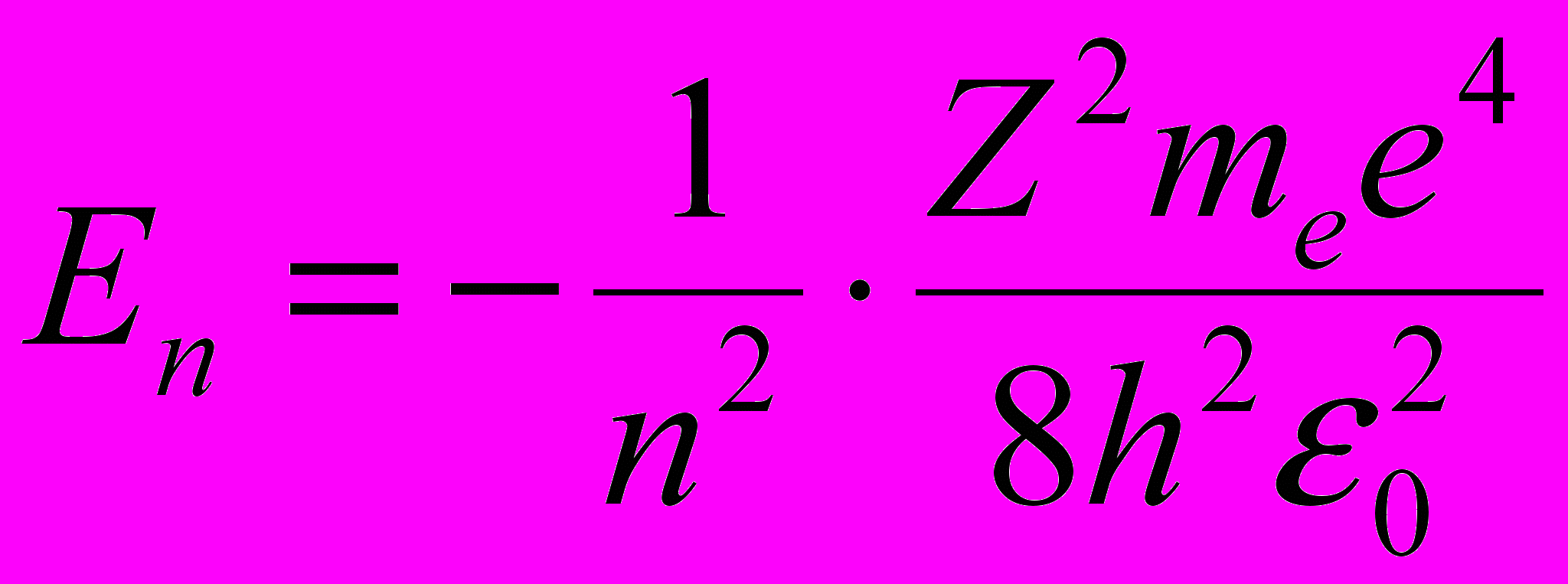
где Z – порядковый номер элемента в системе Менделеева; ε0 – электрическая постоянная; п = 1,2,3, ….

Главное квантовое число п – число, определяющее энергетические уровни атома.

Основное (нормальное) состояние – энергетическое состояние с п=1.

Возбуждённое состояние – энергетическое состояние с n > 1.

Основной (нормальный) уровень – энергетический уровень, соответствующий основному состоянию атома.

Гипотеза де Бройля: с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия Е и импульс р, а с другой – волновые характеристики – частота ν и длина волны λ.

Дебройлевская длина волны частицы:



где р – импульс частицы.

Фазовая скорость частицы массой m, свободно движущейся со скоростью υ:



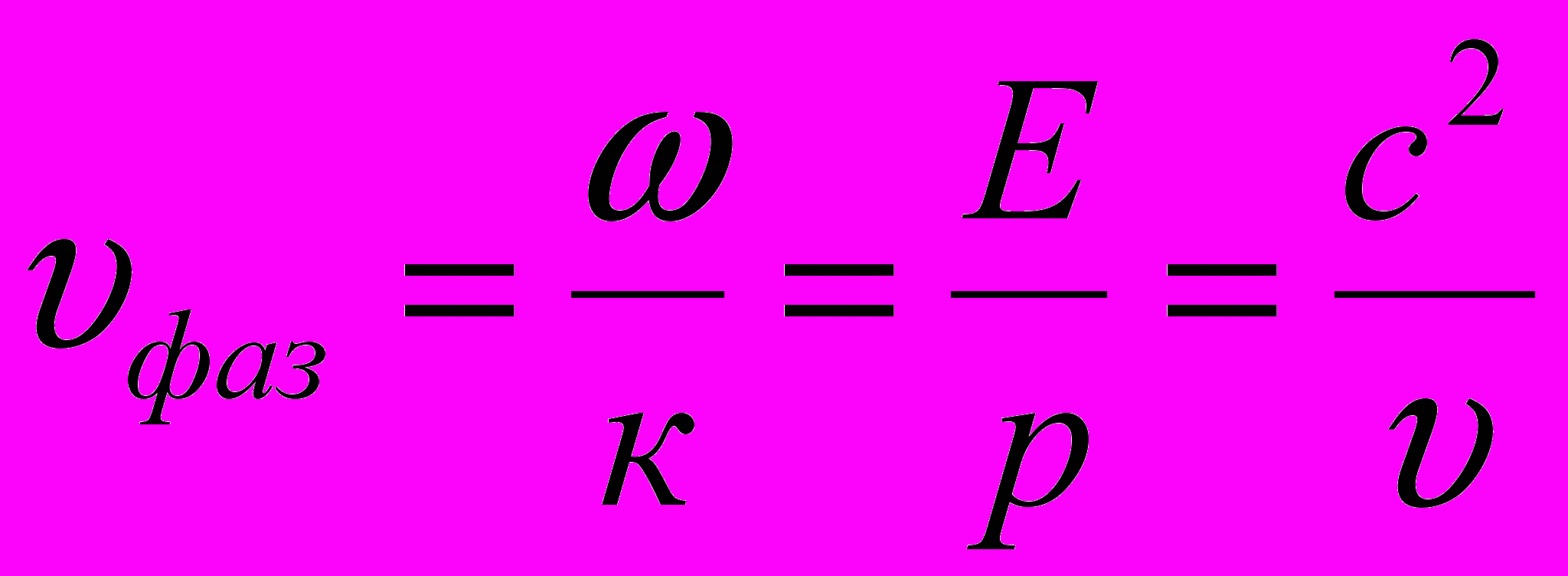
где E = hω – энергия частицы (ω – круговая частота); p = hk – импульс (к = 2π/λ – волновое число).

Групповая скорость свободно движущейся частицы:



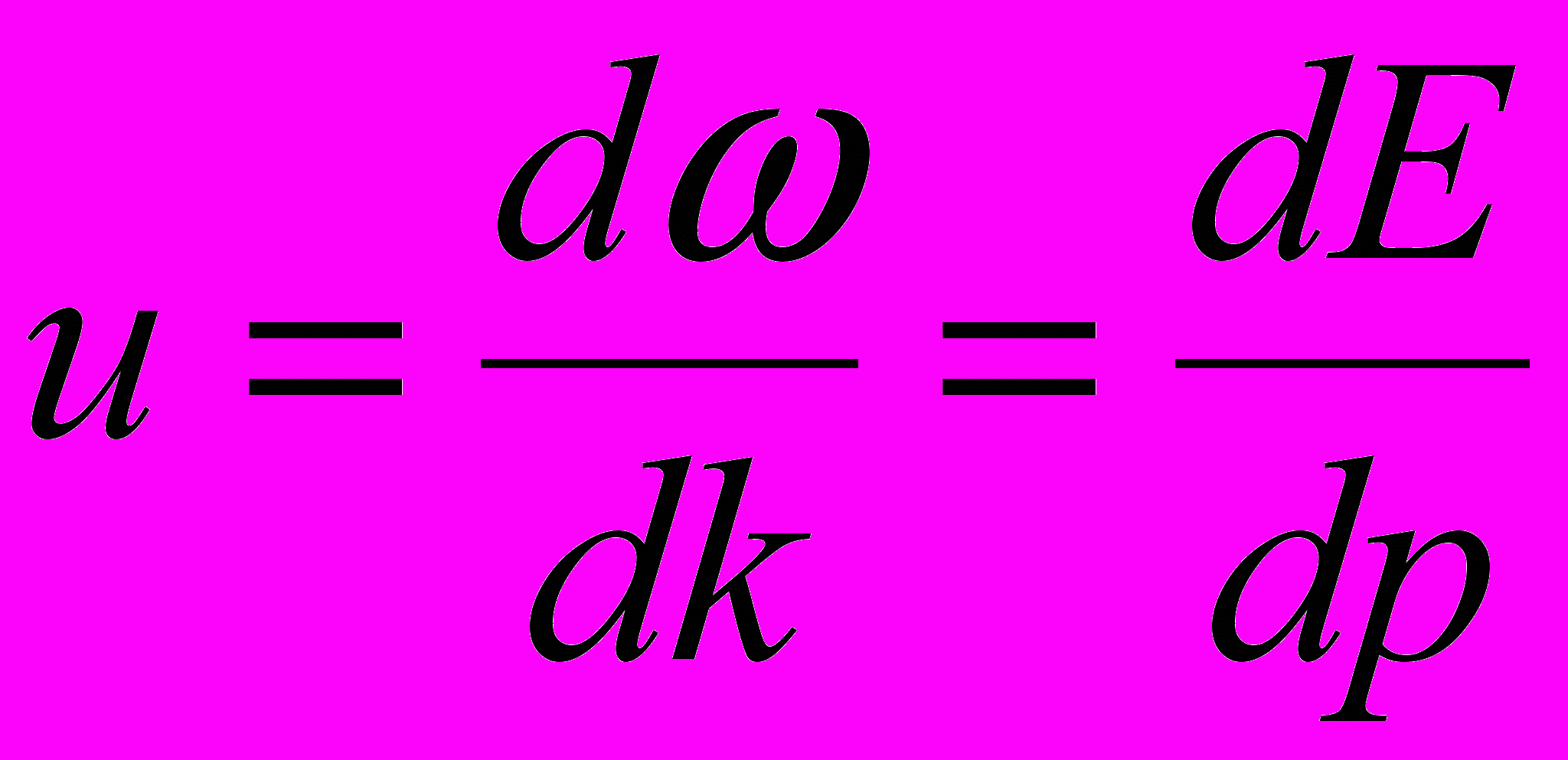
Соотношения неопределённостей: для координаты и импульса частицы:







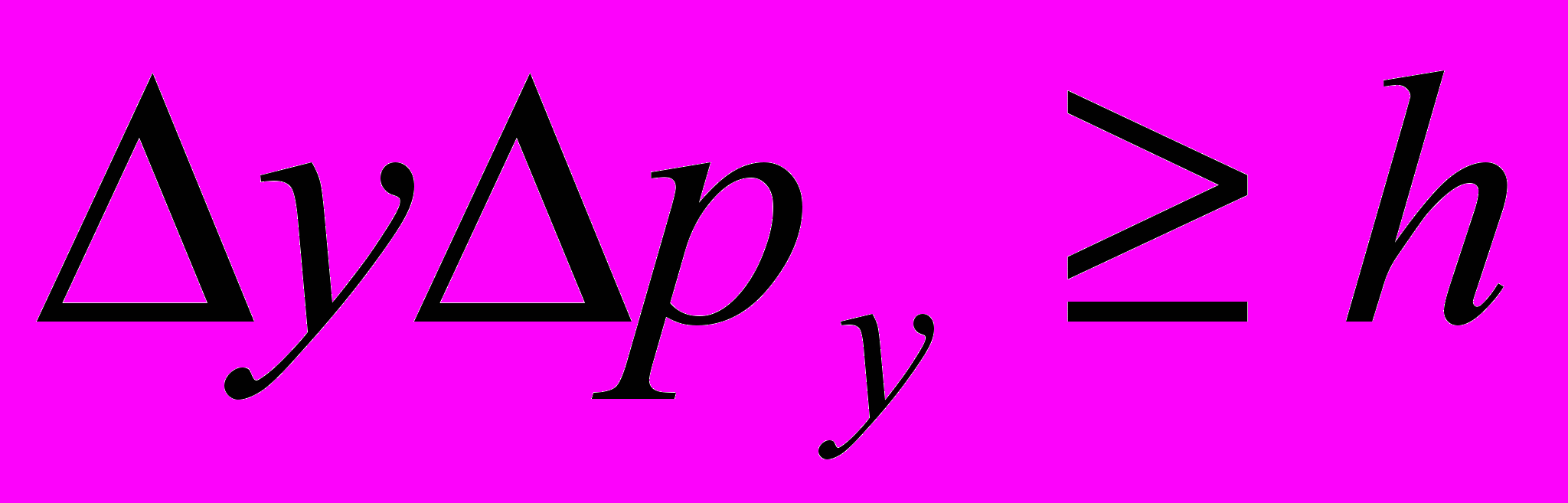
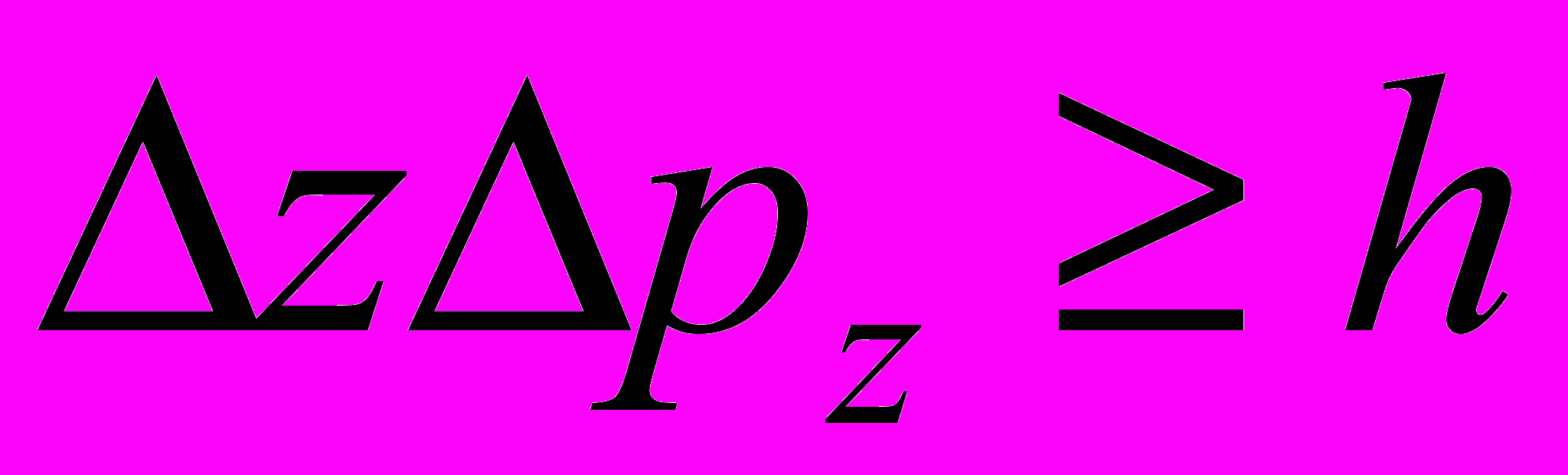
где Δх, Δу, Δz - неопределённости координат; Δрх, Δру, Δрz – неопределённости соответствующих проекций импульса частицы на оси координат;

для энергии и времени:



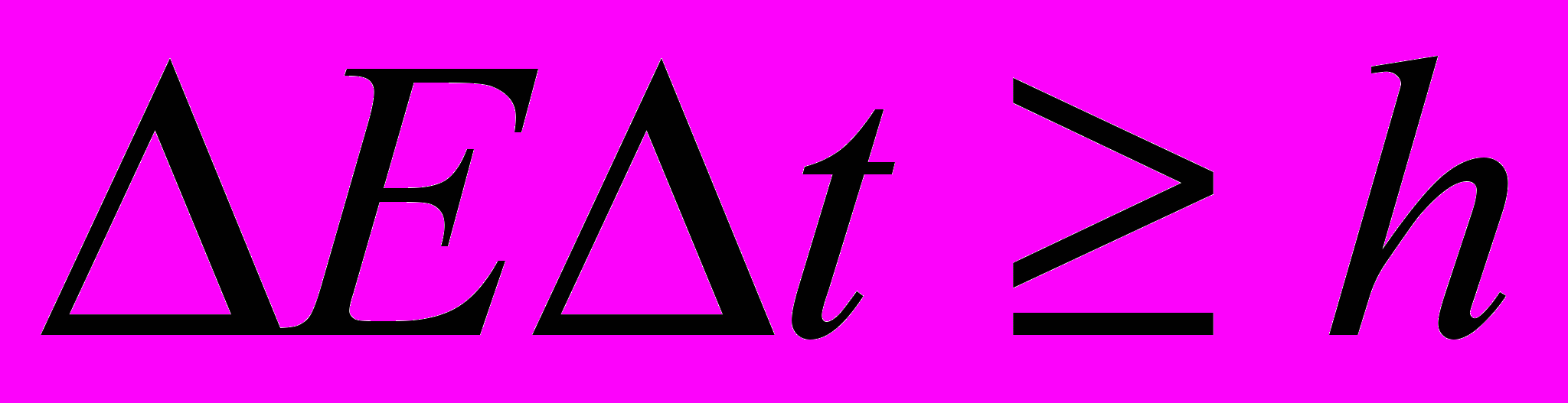
Δ Е – неопределённость энергии данного квантового состояния; Δt – время пребывания системы в данном состоянии.

Вероятность нахождения частицы в объёме dV:



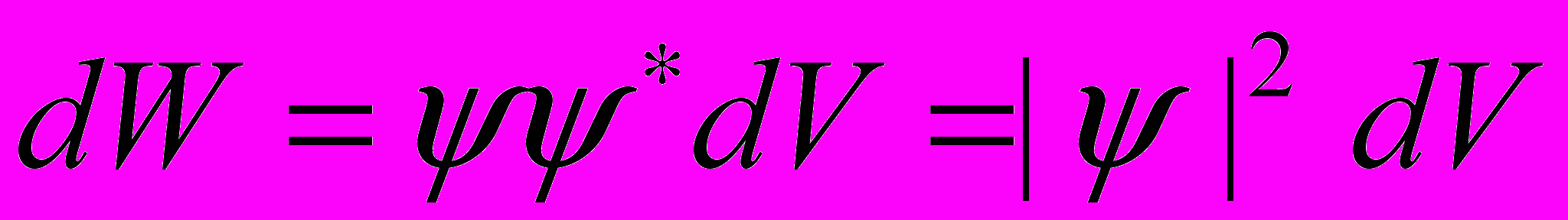
где ψ = ψ (х, у, z, t) – волновая функция, описывающая состояние частицы; ψ* - функция, комплексно сопряжённая с ψ; |ψ|2 = ψ ψ* - квадрат модуля волновой функции.

Плотность вероятности – вероятность нахождения частицы в окрестности точки с координатами х, у, z:



Квадрат модуля волновой функции задаёт интенсивность волн де Бройля.