Методические указания и контрольные задания по физике для слушателей второго курса фзо москва 2004

Вид материала

Содержание

Формула тонкой линзы
Фокусное расстояние линзы
Разность фаз двух когерентных волн
Ширина интерференционной полосы – расстояние между двумя соседними максимумами (или минимумами)
Постоянная (период) дифракционной решётки

Подобный материал:

1 ... 5 6 7 8 9 10 11 12 ... 18

Формула тонкой линзы:

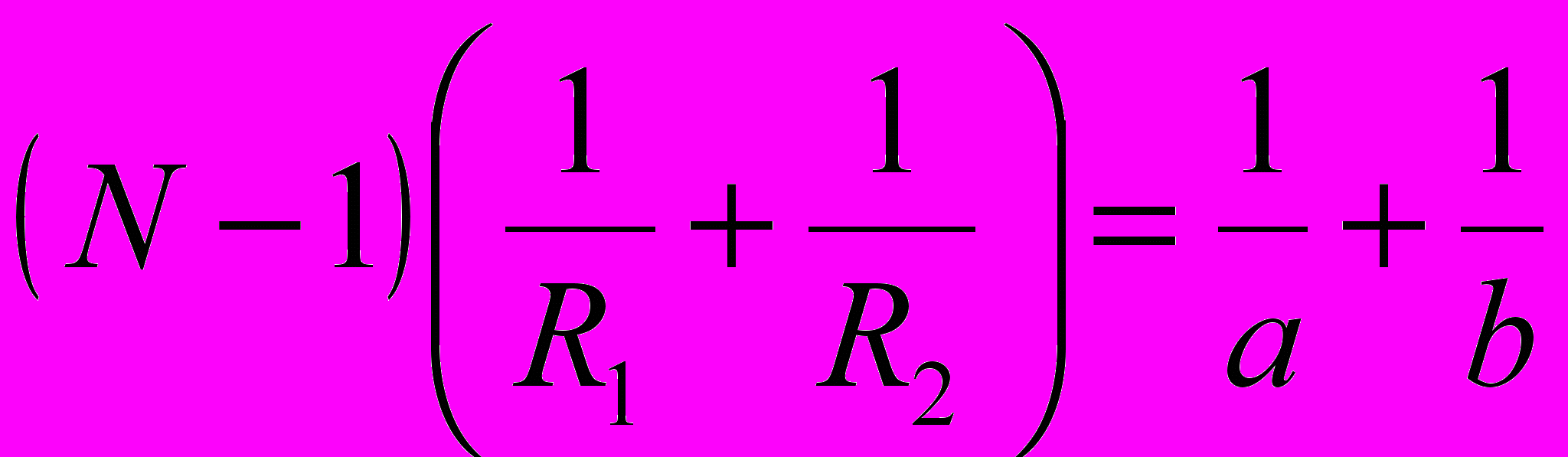
где N = n/n₁ – относительный показатель преломления (п и п₁ – соответственно абсолютные показатели преломления линзы и окружающей среды).

Фокусное расстояние линзы:

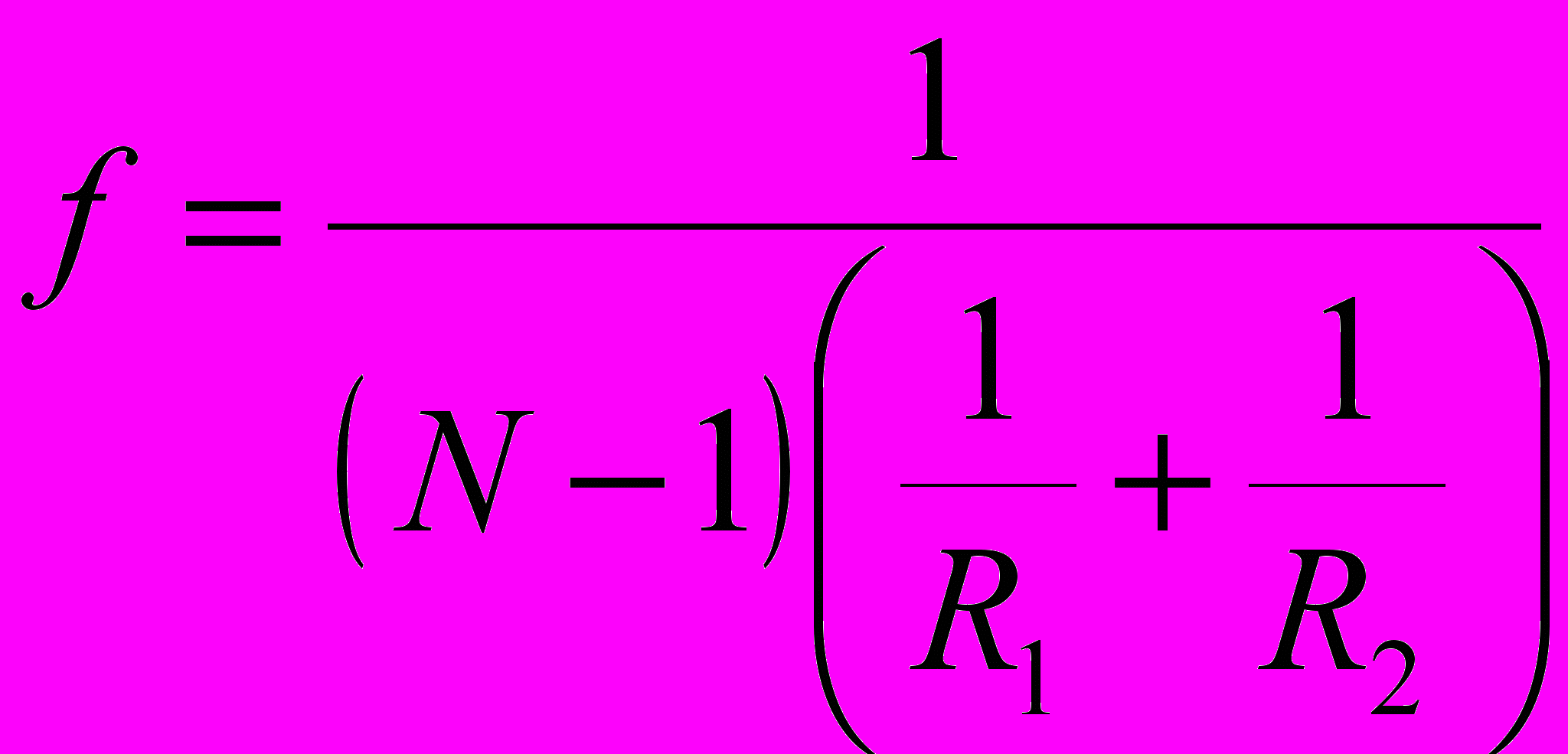
Интерференция света – пространственное перераспределение светового потока при наложении двух (или нескольких) когерентных световых волн, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности.

Разность фаз двух когерентных волн:

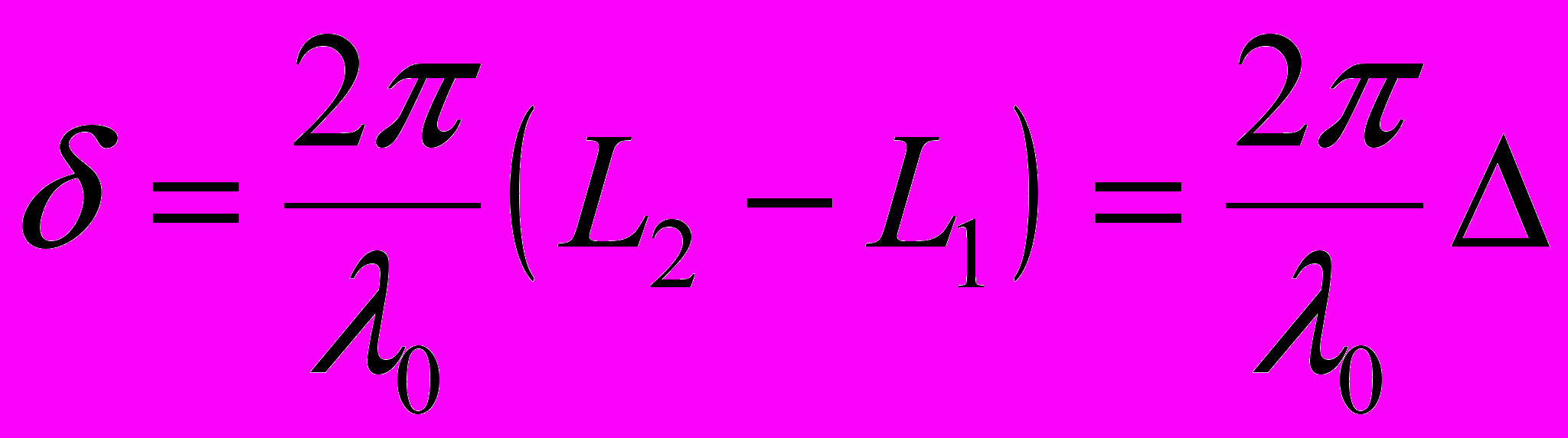
Условие интерференционных максимумов:

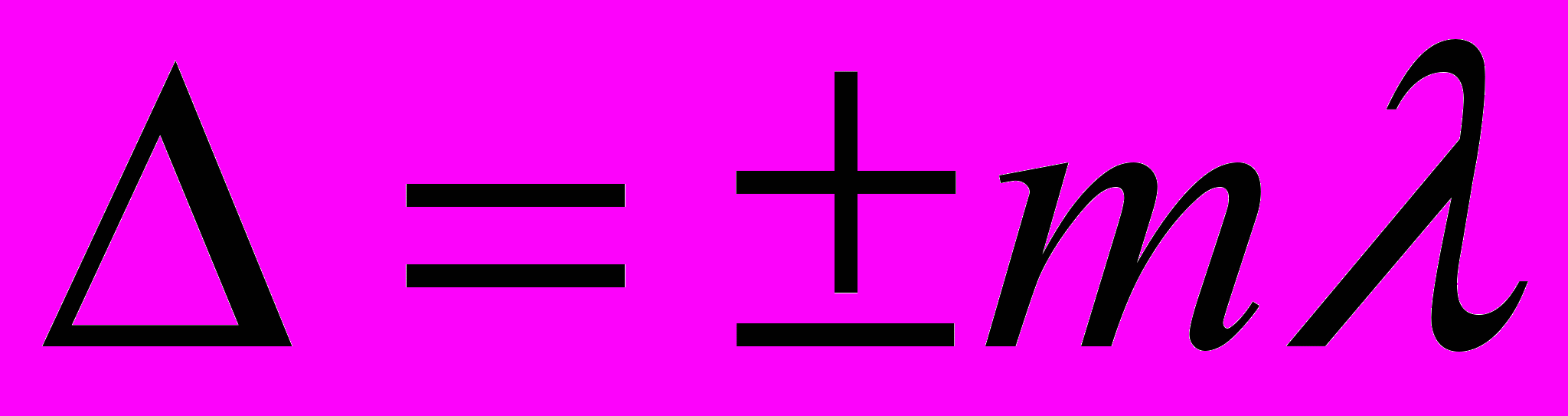
где Δ – оптическая разность хода двух волн, возбуждающих колебания в данной точке, λ – длина волны, m – целое число; m = 0,1,2,….

Условие интерференционных минимумов:

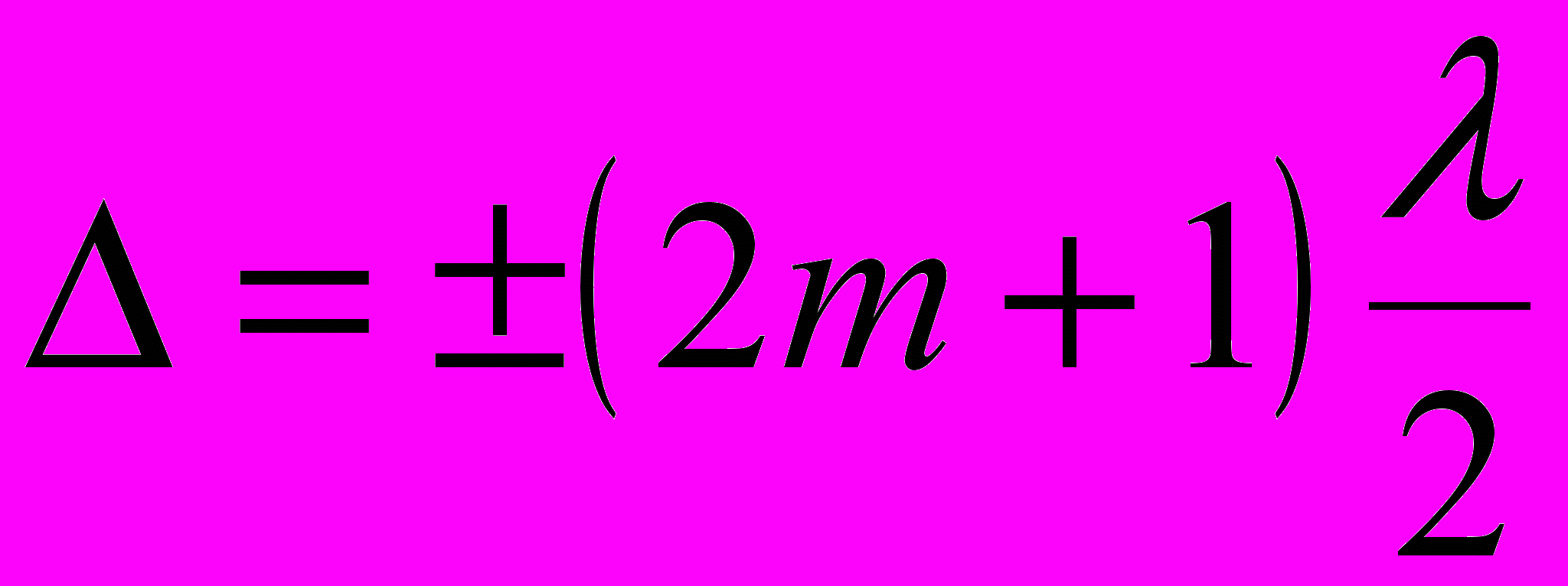
Ширина интерференционной полосы – расстояние между двумя соседними максимумами (или минимумами):

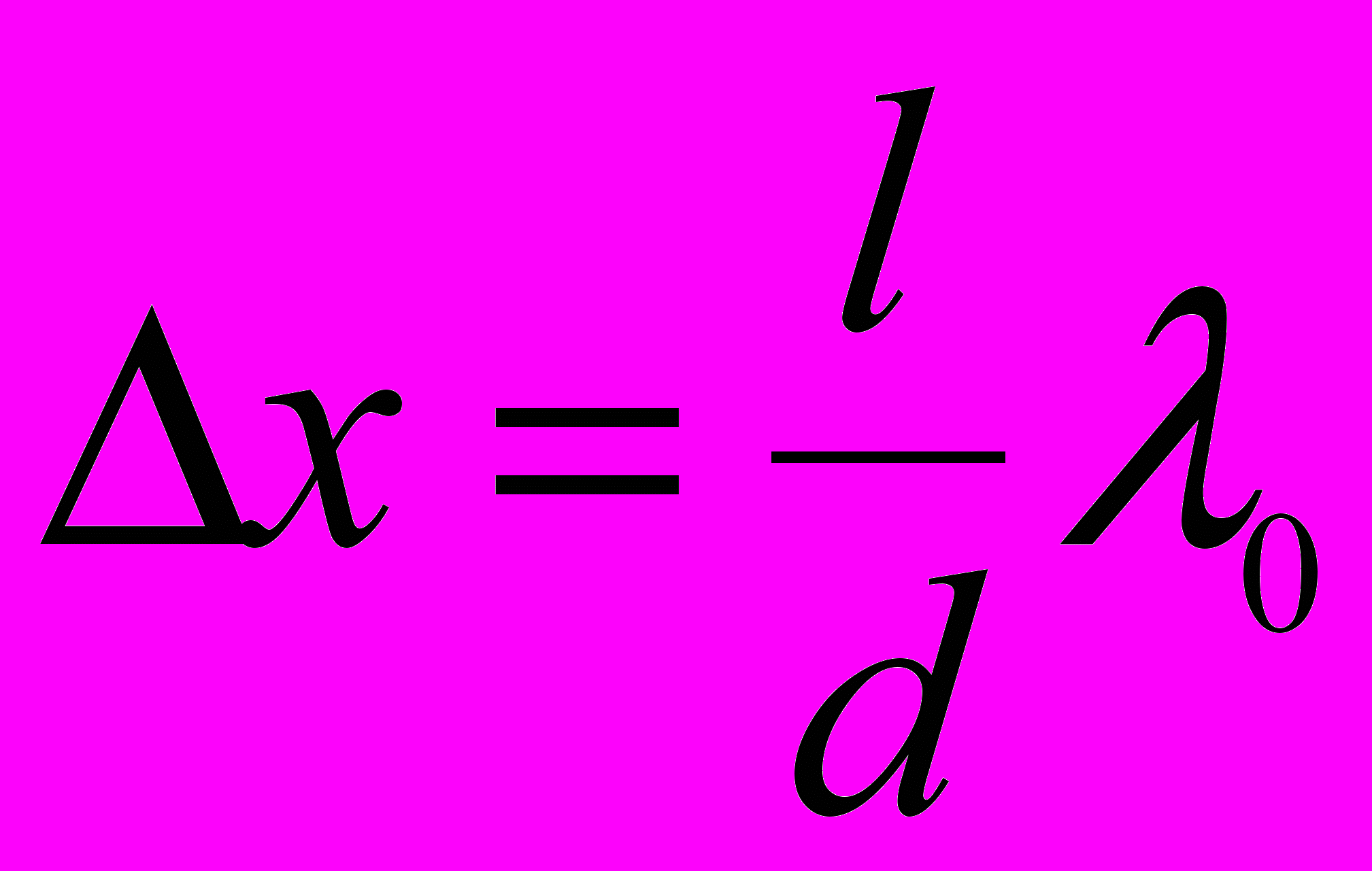
где d – расстояние между когерентными источниками, находящимися на расстоянии l от экрана, параллельного источникам, при условии l >> d.

Оптическая разность хода лучей, отражённых от верхней и нижней поверхностей тонкой плоскопараллельной плёнки, находящейся в воздухе (n₀=1):

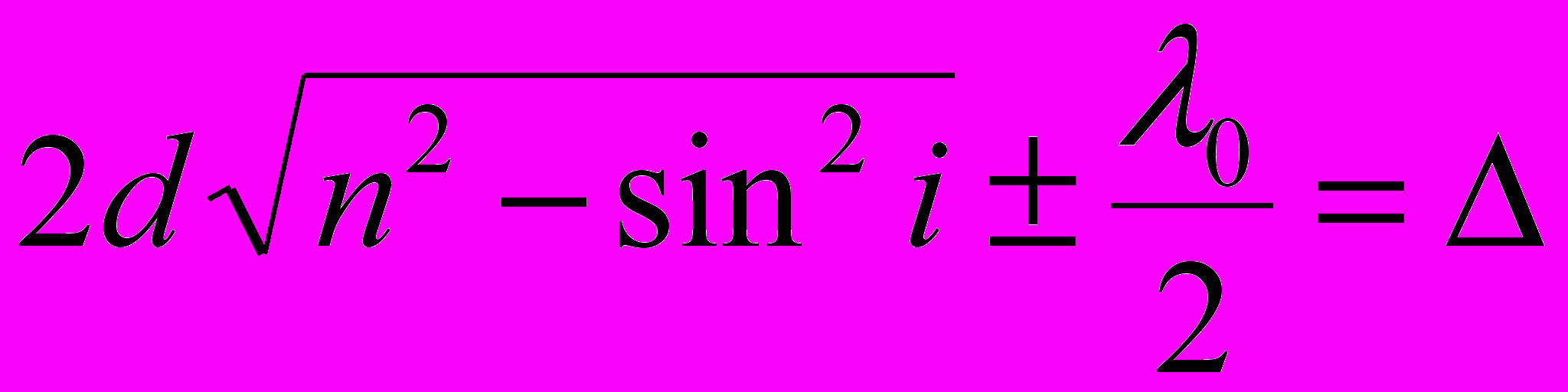
где d – толщина плёнки; n – её показатель преломления; i – угол падения. В общем случае слагаемое ±λ₀/2 обусловлено потерей полуволны при отражении света от границы раздела: если n > n₀, то необходимо выбирать знак плюс, если n < n₀ – знак минус.

Радиусы светлых колец Ньютона в отражённом свете (или тёмных в проходящем свете):

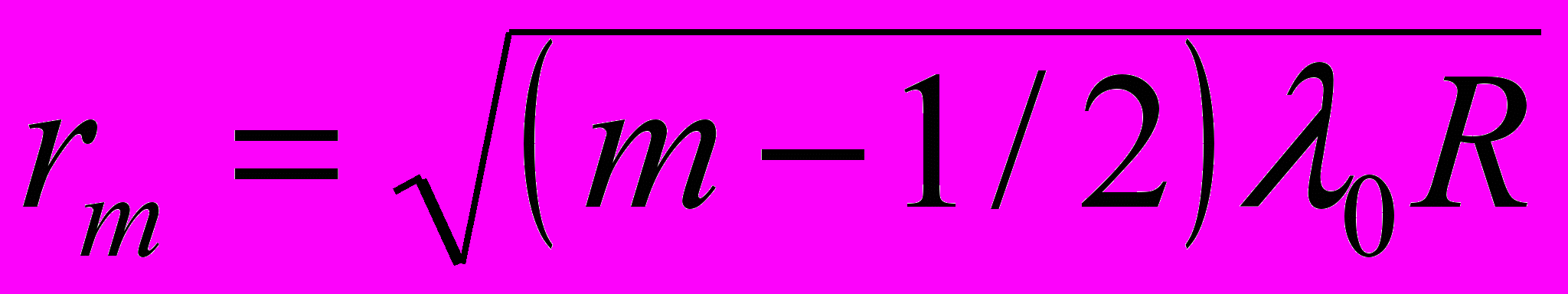
где m = 1,2,3, … - номер кольца, R – радиус кривизны линзы.

Радиусы тёмных колец Ньютона в отражённом свете (или светлых в проходящем свете):

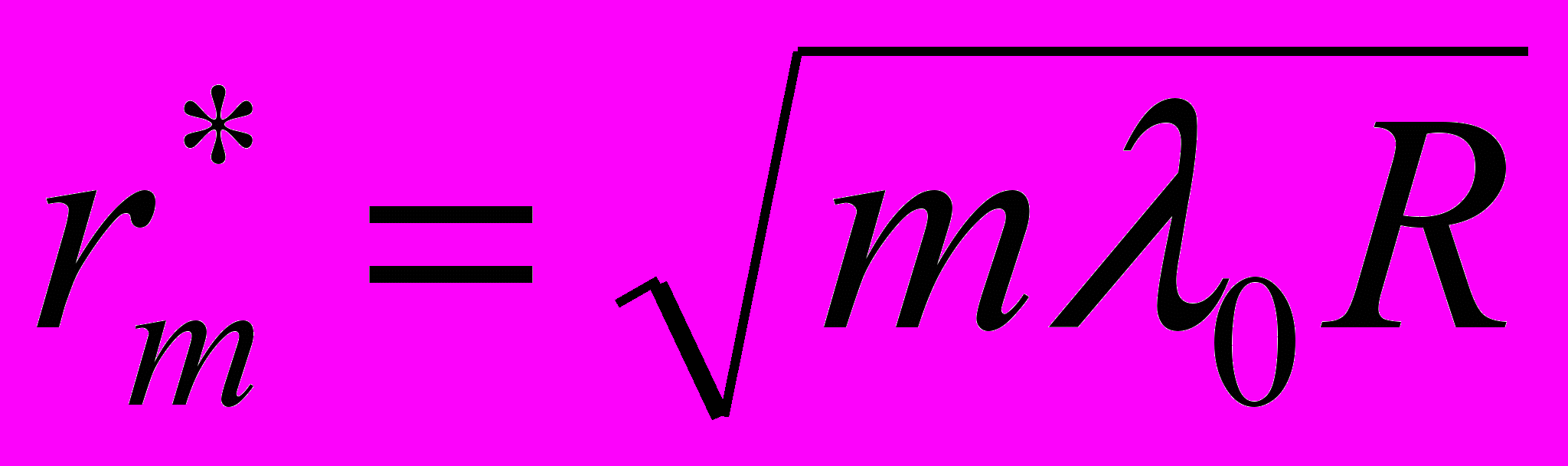
где m = 0,1,2, ….

Дифракция – совокупность явлений, наблюдаемых при распространении света в среде вблизи непрозрачных тел, сквозь малые отверстия и т.д. и связанных с отклонениями от геометрической оптики.

Принцип Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн даёт положение волнового фронта в следующий момент времени.

Принцип Гюйгенса – Френеля: световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками.

Радиус внешней границы m–й зоны Френеля для сферической волны:

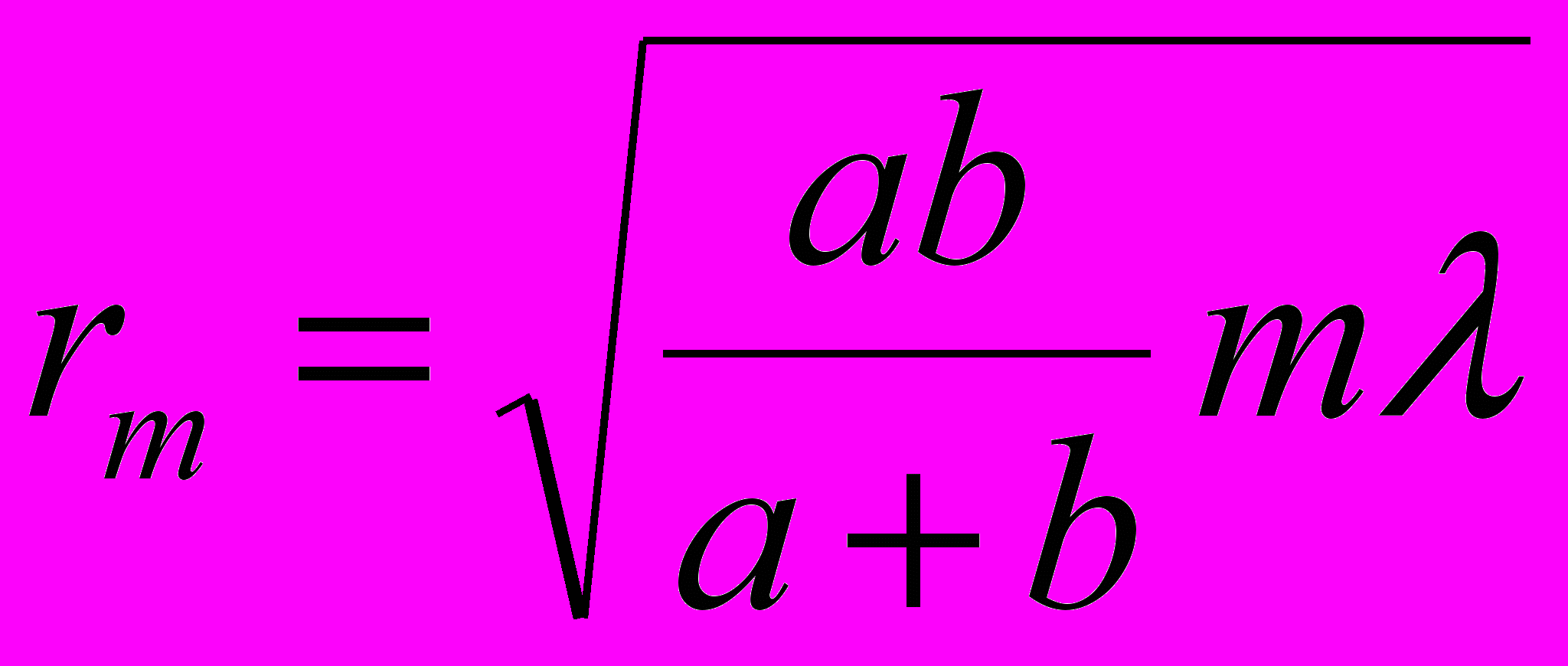
где m – номер зоны Френеля; λ – длина волны, a и b – соответственно расстояния диафрагмы с круглым отверстием от точечного источника и от экрана, на котором дифракционная картина наблюдается.

Условия дифракционных максимумов и минимумов от одной щели, на которую свет падает нормально:

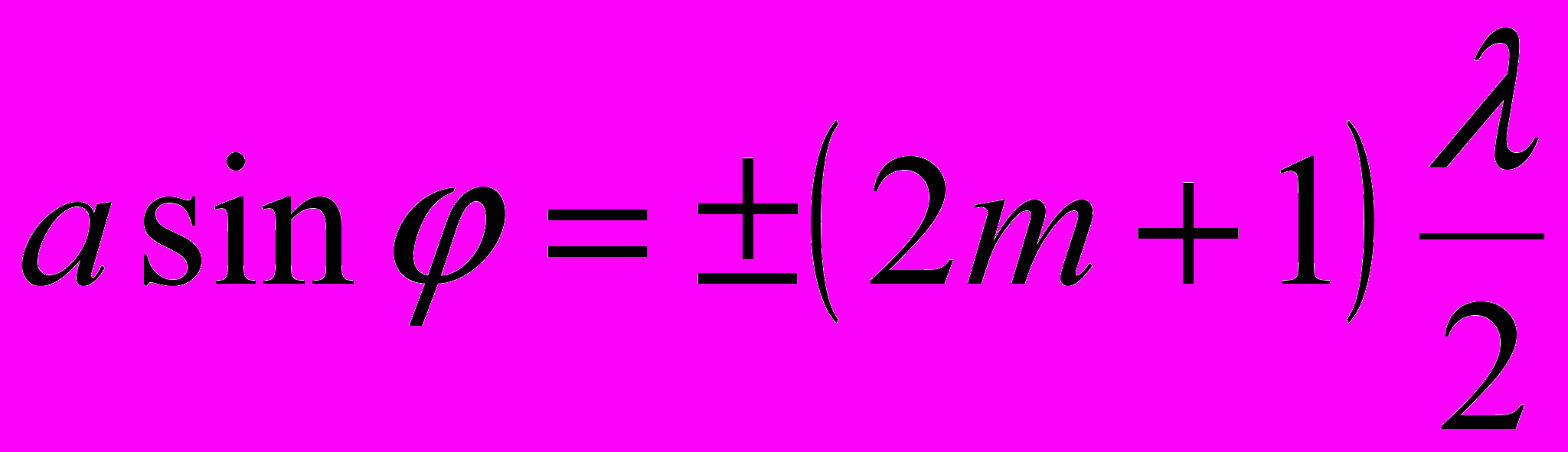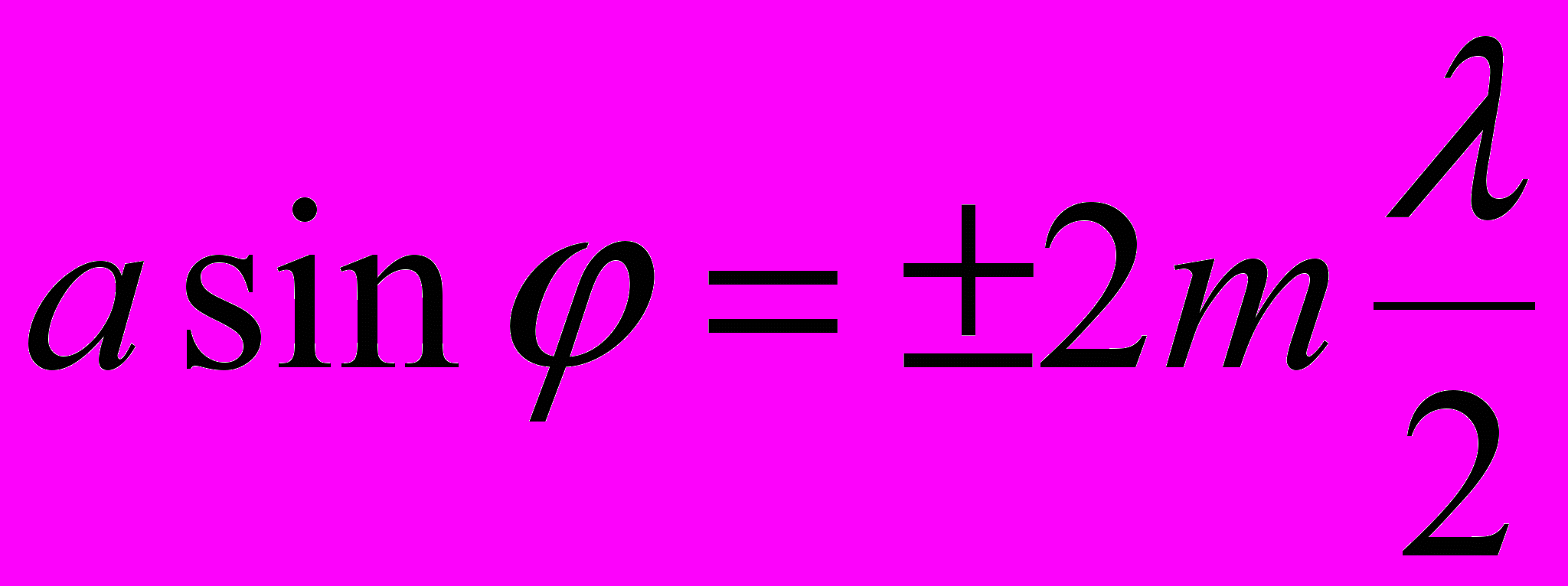
где a – ширина щели; φ – угол дифракции; m = 1,2,3, … - порядок спектра; λ – длина волны.

Одномерная дифракционная решётка – система параллельных щелей равной ширины, лежащих в одной плоскости и разделённых равными по ширине непрозрачными промежутками.

Постоянная (период) дифракционной решётки:

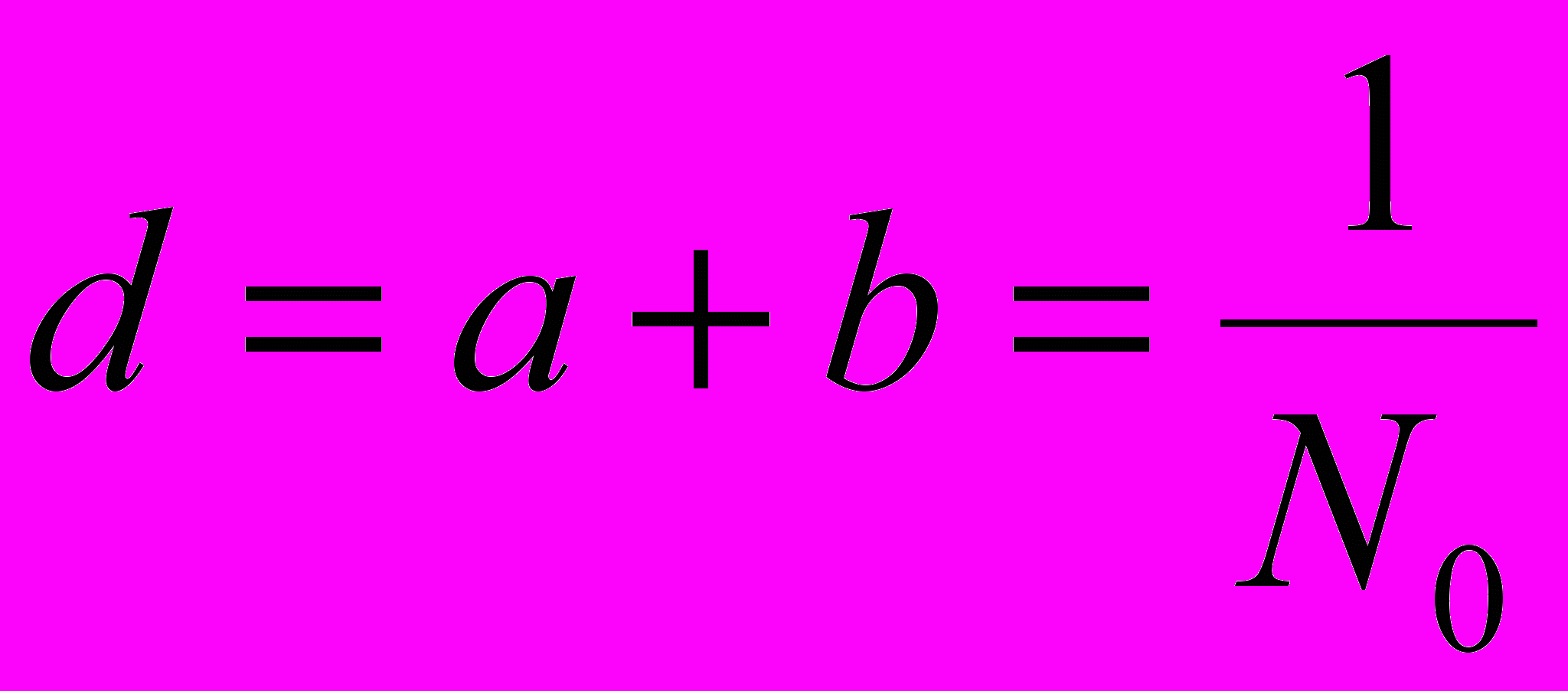
где a – ширина каждой щели решётки; b – ширина непрозрачных участков между щелями.

Условие главных максимумов дифракционной решётки, на которую свет падает нормально:

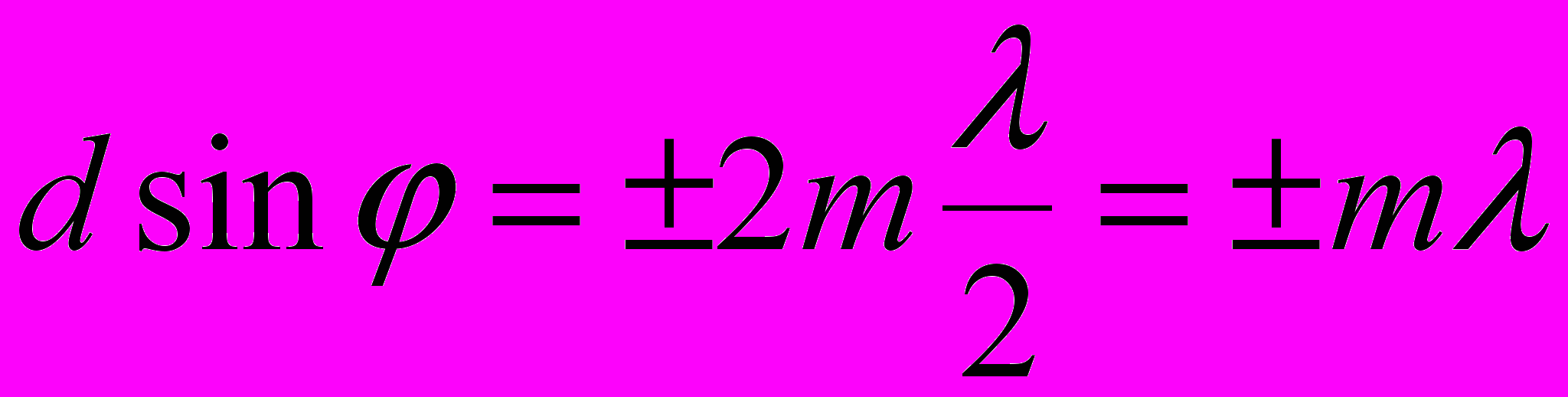
где d – период дифракционной решётки; m = 0,1,2, ….

Условие дополнительных минимумов дифракционной решётки, на которую свет падает нормально:

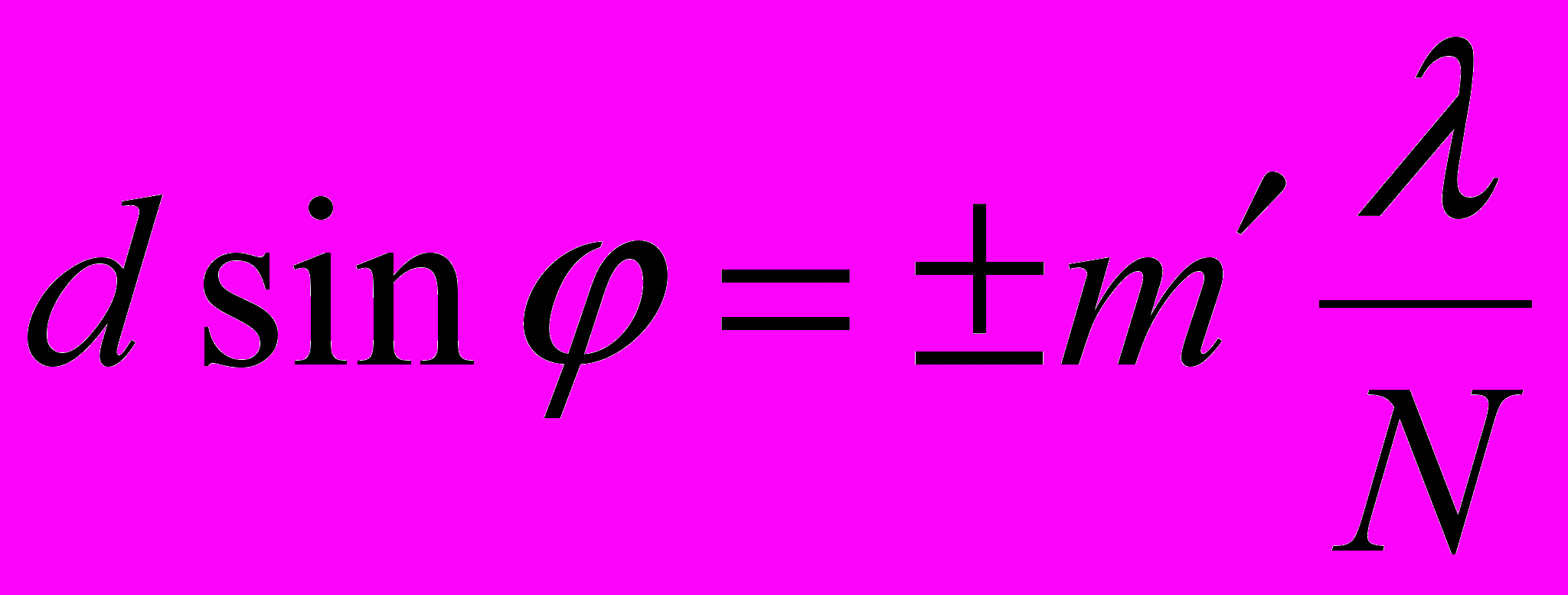
где d – период дифракционной решётки; N – число штрихов решётки; m΄ = 1,2,3, …, кроме 0, N, 2N….

Условие дифракционных максимумов от пространственной решётки (формула Вульфа-Брэгга) :

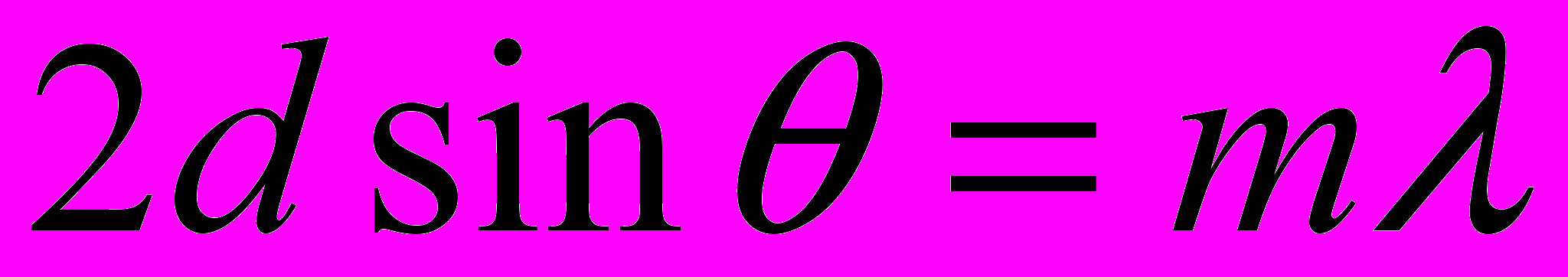
где d – расстояние между атомными плоскостями кристалла;

- угол скольжения; m = 1,2,3, ….

Критерий Рэлея: изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы (разделены для восприятия), если центральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого.