Планирование работы учителя по обучению учащихся решению текстовых задач арифметическим способом
| Вид материала | Методическая разработка |
- Рабочей программы учебной дисциплины методика обучения решению задач уровень основной, 104.55kb.
- Элективный курс по математике, 168.73kb.
- Урок математики в 4 классе по теме «алгебраические и арифметические методы решения, 9.7kb.
- Решение задач занимает в математическом образовании огромное место. Умение решать задачи, 270.04kb.
- Решение задач при изучении математики играет весьма существенную роль, т к. с помощью, 258.56kb.
- Переписка с читателем, 70.86kb.
- «Активизация познавательной деятельности учащихся на уроках математики», 94.77kb.
- Планирование работы на учебный год. Планирование работы на текущий месяц, 15.48kb.
- Элективный курс Морозова Раисия Викторовна, учитель математики, 68.28kb.
- Методика решения текстовых задач в 5-6 классах Учитель математики, 602.73kb.
Или в таком виде:
О
 бъект 1
бъект 1Объект 2 в 3 раза больше
Для составления задач надо учащимся дать ряд указаний:
1. Задача должна иметь все необходимые данные и чётко поставленный вопрос.
2. Предметное содержание и числовые соотношения задачи должны соответствовать действительности.
3. Очень желательно, чтобы числовые данные, хотя бы частично, добывались самими учащимися, для этого рекомендовать использовать журналы, газеты, исторический материал, производственную практику родителей. Составление условия задачи – хорошее упражнение в краткой и точной математической речи.
При таком подходе к составлению задач ясно, что работа эта вызывает большую самостоятельность, интерес, развивает творчество.
Примеры задач на разные темы, составленные учащимися см. приложение 3.
Заключение.
Задачи (в широком смысле этого слова) играют огромную роль в жизни человека. Задачи, которые ставит перед собой человек, и задачи, которые ставят перед ним другие люди и обстоятельства жизни, направляют всю его деятельность, всю жизнь. Мышление человека главным образом состоит из постановки и решения задач.
В конце 60-х годов ХХ века арифметические способы решения задач посчитали анахронизмом и перешли к раннему использованию уравнений. Но без достаточной подготовки мышления учащихся это оказалось малоэффективным. Опыт моей работы в школе это подтверждает. За 17 лет работы я могу по памяти перечислить всех учеников, которые умели решать задачи.
Таким образом, можно сделать следующие выводы:
1) Исторически люди пришли к применению уравнений, обобщая решения задач, в которых приходилось оперировать с неизвестным числом. Ребёнок должен пройти тот же путь – сначала рассуждать о «частях», опираясь на воображаемые действия с конкретными предметами или величинами, и лишь потом прийти к применению уравнений. За этот путь говорят и особенности мышления учащихся, тяготеющего к оперированию наглядными образами.
2) На данном этапе обучения (5-6 класс) арифметические способы решения задач имеют преимущество перед алгебраическими уже потому, что результат каждого отдельного шага в решении по действиям имеет совершенно наглядное и конкретное истолкование, не выходящее за рамки опыта учащихся. Мышление пятиклассников конкретно, и развивать его надо в деятельности с конкретными объектами и величинами или их образами, чем мы и занимаемся при арифметическом решении задач.
3) Несмотря на небольшое количество часов, отведённое программой на изучение математики (5 часов в неделю), можно продумать и организовать работу с задачами таким образом, что ребёнок, опираясь на наглядность, будет переходить от простого к сложному, от практических действий с предметами к воображаемым действиям с данными в задаче величинами. Тем самым будет достигнута истинная цель обучения, заключающаяся не столько в освоении школьниками конкретных способов деятельности, сколько в развитии их мышления и практических умений в процессе освоения этих способов деятельности.
Невозможно изобрести универсальную методику обучения решению задач, пригодную для всех детей и во всех случаях. Это всё равно, что искать лекарство от всех болезней. Предложенная методическая разработка - один из вариантов специальным образом организованной работы учителя с задачами.
Такая система работы даёт положительные результаты.
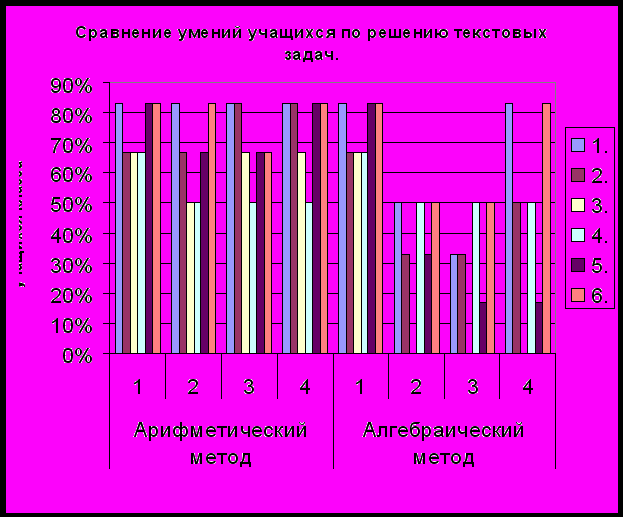
Я проанализировала некоторые умения учащихся по решению текстовых задач в одном классе. Для наглядности я сравнила умения учащихся выполнять работу на каждом их 4-х этапов решения задачи (цифры по горизонтальной оси) разными методами. Под цифрами 1-6 я рассмотрела следующие типы задач:
1.Решение задач на нахождение двух или нескольких чисел по их сумме (разности) и отношению.
2. Решение задач на нахождение двух или нескольких чисел по их сумме и разности.
3. Решение задач на движение.
4. Решение задач на предположение.
5. Решение задач на нахождение части от числа и числа по его части.
6. Решение задач на пропорциональную зависимость.
Результаты отражены в следующей диаграмме.
СПИСОК ЛИТЕРАТУРЫ
1. Аргинская И.И., Вороницына Е.В. Особенности методики работы по обучению учащихся решению текстовых задач.// Начальная школа, 2005 №24
2. Арифметика: Учебник для 5 кл./ С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин – М.: Просвещение, 2003
3. Арифметика: Учебник для 6 кл./ С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин – М.: Просвещение, 2000
4. Математика: Учебник для 5 кл./ Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков,С.И.Шварцбурд – М.: Мнемозина, 2004
5. Математика: Учебник для 6 кл./ Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков,С.И.Шварцбурд – М.:Просвещение, 1994
6. Математика: Учебник для 5 кл./ Под ред Г.В.Дорофеева, И.Ф. Шарыгина – М.:Просвещение, 2003
7. Математика: Учебник для 6 кл./ Под ред Г.В.Дорофеева, И.Ф. Шарыгина – М.:Дрофа, 2000
8. Программа по математике: авт. М.И. Моро, Ю.М. Колягин, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова//Программы общеобразовательных учреждений, нач. классы (1 – 4) ч.1. – М.: «Просвещение», 2002
9. Программа по математике: авт. Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд //Программы для общеобразовательных школ, гимназий, лицеев, 5-11 кл. – М.: Дрофа, 2000.
10. Саговская Е.Н. Активизация работы ученика над арифметической задачей //Из опыта преподавания математики в 5-7 классах средней школы – М.: Учпедгиз, 1954
11. Саговская Е.Н. Методические разработки по арифметике – М.: Учпедгиз, 1959
12. Талызина Н.Ф.Формирование общих приёмов решения арифметических задач//Формирование приёмов математического мышления - М.: ТОО «Вентана --Граф», 1995
13. Шарова О.П. Сюжетные задачи в обучении математике
14. Шарова О.П. О некоторых аспектах методики обучения учащихся решению сюжетных задач арифметическим методом
15. Шевкин А.В. Обучение решению текстовых задач в 5-6 классах. – М.: Русское слово, 2002
16. Шевкин А.В. Текстовые задачи в школьном курсе математики //Математика, 2005 - №17-20.
17. Фридман Л.М. Как научиться решать задачи – М.: Просвещение, 1984
Приложение 1.
Тренировочные задачи на закрепление основных арифметических действий.
1. У одного мальчика16 марок, а у другого 27 марок. Сколько марок у обоих мальчиков вместе?
2. В первый день продали 25 кг яблок, во второй – 40 кг, а в третий день продали 55 кг яблок. Сколько яблок продали за три дня?
3. В первом классе начальной школы 12 учеников, во втором классе -9 учеников, в третьем – 11 учеников, а в четвёртом – 8 учеников. Сколько учеников всего в начальной школе?
4. В жёлтой папке 20 листов, а в красной – 35 листов. Сколько листов в двух папках ?
5. В одном куске15 м проволоки, а в другом на 5 м больше. Сколько метров проволоки во втором куске ?
6. У Алеши в кармане 23 ореха, а у Вани на 5 орехов меньше. Сколько орехов в кармане у Вани?
7. В первый день отремонтировали 13 км дороги, и это на 5 км больше, чем во второй день. Сколько километров дороги отремонтировали во второй день?
8. Сыну 5 лет, он моложе отца в 6 раз. Сколько лет отцу?
9. В первый день бригада собрала 700 кг картофеля, а во второй день в 2 раза больше, чем в первый. Сколько килограммов картофеля собрала бригада во второй день?
10. В первой корзине в 3 раза меньше грибов, чем во второй. Сколько грибов в первой корзине, если во второй 9 кг грибов?
11. Николаю 12 лет, а Игорю 7 лет. Кто из мальчиков старше и на сколько?
12. В одной книге 300 страниц, а в другой 100. Во сколько раз количество страниц во второй книге меньше количества страниц в первой книге?
13. Книга стоит 65 рублей, а блокнот 13 рублей. Во сколько раз книга дороже блокнота, на сколько рублей блокнот дешевле книги?
14. За 5 карандашей заплатили 15 рублей. Сколько стоит один карандаш?
15. Двадцать ящиков весят 300 кг. Сколько килограммов весит один ящик?
16. В зале 20 рядов. В каждом ряду 25 стульев. Сколько всего стульев в зале?
17. 600 конфет положили в коробки. Сколько коробок потребовалось, если в каждую коробку входит 60 конфет?
18. На изготовление десяти сарафанов пошло 20 метров ситца. Сколько материи пошло на изготовление одного сарафана?
19. В баке было 20 литров бензина. По дороге 8 литров израсходовали. Сколько литров бензина осталось в баке?
20. От куска верёвки длиной 20 метров отрезали часть, после чего осталось 5 метров. Сколько метров отрезали?
21. В магазине было 200 кг фруктов. Сколько кг фруктов стало в магазине после того, как туда завезли ещё 40 кг?
Приложение 2.
Примерное тематическое планирование
учебного материала по математике в 5-6 классах.
(решение текстовых задач арифметическим способом)
по учебникам авторов Н.Я.Виленкина, В.И.Жохова, А.С.Чеснокова, С.И.Шварцбурд, 2004г.
5 класс
Всего – 170 часов, по 5 часов в неделю.
| № урока | Тема урока | Количество часов |
| 1. НАТУРАЛЬНЫЕ ЧИСЛА И ШКАЛЫ. 18 ч | ||
| 1-3 | Обозначение натуральных чисел. Решение задач на отработку отношений «на…больше», «на…меньше», «всего». | 3ч |
| 4-8 | Отрезок. Треугольник. Плоскость. Прямая. Луч. Решение задач на отработку отношений «на…больше», «на…меньше», «в…раз больше», «в…раз меньше», «всего» применительно к отрезкам. Нахождение периметра многоугольника. | 5ч |
| 9-11 | Шкалы и координаты. | 3ч |
| 12-14 | Меньше или больше. Решение задач на разностное сравнение величин. | 3ч |
| 15 | к/р №1 | 1ч |
| 16-18 | Резервные уроки. | 3ч |
| 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ. 15ч | ||
| 19-23 | Сложение N-чисел и его свойства. Вычитание N-чисел. Решение простых и составных задач на применение действий сложения и вычитания N-чисел. | 5ч |
| 24 | к/р№2. | 1ч |
| 25-29 | Числовые и буквенные выражения. Составление числовых и буквенных выражений к решению задач. | 5ч |
| 30-32 | Уравнения. | 3ч |
| 33 | к/р №3 | 1ч |
| 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ. 26ч | ||
| 34-37 | Умножение N-чисел и его свойства. Решение задач на отработку отношений: единица товара-количество товара-всего. | 4ч |
| 38-44 | Деление N-чисел. Решение задач на процессы с одним участником действия. -формирование понятия о времени; -формирование понятия о скорости протекания процесса; -решение и составление задач на процессы | 1ч 1ч 2ч |
| 45 | Деление с остатком. Решение задач, приводящих к делению с остатком. Решение задач на процессы с несколькими участниками. | 1ч 4ч |
| 46 | к/р №4 | 1ч |
| 47-51 | Упрощение выражений. Решение задач на части. -нахождение двух величин по их сумме и отношению; -нахождение двух величин по их разности и отношению. | 3ч 2ч |
| 52-54 | Порядок выполнения действий. Квадрат и куб числа. Решение задач, приводящих к делению ,умножению N-чисел | 3ч |
| 55 | к/р №5 | 1ч |
| 56-57 | Резервные уроки | 3ч |
| 4. ПЛОЩАДИ И ОБЪЁМЫ. 15 ч | ||
| 58-60 | Формулы. Решение задач на движение. | 3ч |
| 61-63 | Площадь. Формула площади прямоугольника. Решение задач на нахождение площади прямоугольника и квадрата. | 3ч |
| 64-66 | Единицы измерения площадей Решение задач на предположение. | 3ч |
| 67-68 | Прямоугольный параллелепипед. | 2ч |
| 69-71 | Объёмы. Объём прямоугольного параллелепипеда. | 3ч |
| 72 | к/р №6 | 1ч |
| 5. ОБЫКНОВЕННЫЕ ДРОБИ. 26ч | ||
| 73-74 | Окружность и круг. | 2ч |
| 75-77 | Доли. Обыкновенные дроби. Решение задач на нахождение части от числа и числа по его части. | 4ч |
| 78-80 | Сравнение дробей. Отработка умения решать задачи на нахождение части от числа и числа по его части. | 3ч |
| 81-82 | Правильные и неправильные дроби | 2ч |
| 83 | к/р №7 | 1ч |
| 84- 86 | Сложение и вычитание дробей с одинаковыми знаменателями. Решение задач, приводящих к сложению и вычитанию дробей с одинаковыми знаменателями. | 3ч |
| 87-88 | Деление и дроби. Решение задач, приводящих к делению и получению нецелого числа. | 2ч |
| 89-94 | Смешанные числа. Сложение и вычитание смешанных чисел. Решение задач, приводящих к сложению и вычитанию смешанных чисел. | 6ч |
| 95 | к/р №8 | 1ч |
| 96-98 | Резервные уроки | 2ч |
| 6. ДЕСЯТИЧНЫЕ ДРОБИ.СЛОЖЕНИЕ И ВЫЧИТАНИЕ. 15ч | ||
| 99-100 | Десятичная запись дробных чисел. | 2ч |
| 101-103 | Сравнение десятичных дробей | 3ч |
| 104-108 | Сложение и вычитание десятичных дробей. Решение задач, приводящих к сложению и вычитанию десятичных дробей.( отношения «на…больше», «на…меньше», «всего», нахождение разницы между величинами.) | 5ч |
| 109-111 | Округление чисел. Округление чисел в текстовых задачах. | 3ч |
| 112 | к/р №9 | 1ч |
| 113 | Резервные уроки | 1ч |
| 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ. 25ч | ||
| 114-117 | Умножение десятичных дробей на N-число. Решение задач, приводящих к умножению десятичных дробей на N-число. | 4ч |
| 118-121 | Умножение десятичных дробей на десятичную дробь. Решение задач, приводящих к умножению десятичных дробей на десятичную дробь.(Решение задач на движение по реке.) | 4ч |
| 122-126 | Деление десятичных дробей на N-число. Решение задач, приводящих к делению десятичных дробей на десятичную дробь.(Решение задач на движение по реке.) | 5ч |
| 127-132 | Деление на десятичную дробь. Отработка действий с десятичными дробями при решении задач различных видов. | 6ч |
| 133-136 | Среднее арифметическое чисел. Решение задач на нахождение среднего арифметического чисел. | 3ч |
| 137 | к/р №10 | 1ч |
| 138-139 | Резервные уроки | 2ч |
| 8. ИНСТРУМЕНТЫ ДЛЯ ВЫЧИСЛЕНИЙ И ИЗМЕРЕНИЙ. 17ч | ||
| 140-141 | Микрокалькулятор | 2ч |
| 140-145 | Проценты. Решение задач на проценты: -нахождение части от числа, выраженной в % от этого числа; -нахождение самого числа по части от этого числа, выраженной в %; -нахождение процентного отношения чисел | 6ч |
| 146 | к/р №11 | 1ч |
| 147-151 | Углы. Измерение углов. | 5ч |
| 152-153 | Круговые диаграммы. | 2ч |
| 154 | к/р №12 | 1ч |
| 155-170 | Итоговое повторение. Решение задач разных типов. | 16ч |
