Решение задач при изучении математики играет весьма сущест­венную роль, т к. с помощью задач рассматриваются основные теорети­ческие положения в курсе математики.

Вид материала

Решение

Содержание 6. Теоретико-методические особенности поиска способов решения задач. Прямая связь Косвенная связь Решение задач разными способами.

Подобный материал:

• Практикум: «Изучение процентов в школьном курсе математики», 90.4kb.
• Решение олимпиадных задач принципиально отличается от решения школьных, даже очень, 474.21kb.
• Решение задач в начальной школе имеет центральное значение для развития мышления учащихся:, 114.44kb.
• Методика обучения решению прикладных задач в школьном курсе математики примерное содержание, 14.61kb.
• Методика формирования новых понятий в курсе математики примерное содержание, 8.98kb.
• Данная работа посвящена теоретическим и практическим аспектам внедрения в начальный, 344.19kb.
• Календарно-тематическое планирование по учебному курсу «Математика», 542.18kb.
• Программа дисциплины фтд. 00 «практикум по решению математических задач» Специальность, 275.82kb.
• План: Введение. Понятие текстовой задачи. Виды арифметических задач. Роль задачи, 1075.19kb.
• Урок математики в 7-м классе по теме "Решение задач с помощью систем уравнений", 63.6kb.

ОРГАНИЗАЦИЯ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ ПРИ РЕШЕНИИ ТЕКСТОВЫХ ЗАДАЧ.


1. Решение задач при изучении математики играет весьма сущест­венную роль, т.к. с помощью задач рассматриваются основные теорети­ческие положения в курсе математики. При изучении математики в начальных классах дети должны научиться самостоятельно находить пути решения прос­тых и несложных составных задач, а для этого они должны овладеть элементарными общими, в то же время разнообразными приёмами подхода к ре­шению таких задач. В методической литературе неоднократно поднимается вопрос о необходимости совершенствования обучения младших школьников решению текстовых математических задач, в связи с интенсивно разраба­тываемой методикой развивающего обучения.

Задачи и решение их занимают в обучении школьников весьма существенное место и по времени, и по их влиянию на умственное разви­тие ребёнка. Роль решаемой задачи зависят от того, какую педагогичес­кую цель ставит учитель, предлагая ту или иную задачу. Довольно часто рассмотрение и решение задачи выполняет роль трамплина, от которого должен оттолкнуться ученик, чтобы понять суть, практический смысл и значение изучаемого раздела теории. В этом случае решение задач спо­собствует формированию математических понятий.

Значительно чаще задача предлагается ученикам для пополнения их знаний, приобретения умений, для совершенствования и закрепления навыков. В этом случае цели решения задач шире и сводятся к следующему:

1. Установить причинно-следственные связи и раскрыть функциональную зависимость между величинами, входящими в условие задачи.

2. Научиться умению логически правильно рассуждать и делать обоснованные умозаключения при выяснении хода решения задач.

3. Обоснованно выбирать арифметические действия и выполнять их безошибочно.

4. Ознакомиться с решением задач определенного вида.

При этом работа с задачами преследует и широкие воспитательные цели:

1. Задачи, воспитывающие любовь к Родине, родному краю.
   
2. Многие задачи готовят учеников применять в жизненной и учебной практике приобретённые ими знания.
   
3. Поиск решения развивает настойчивость, воспитывает волю.
   
4. Участие в творческом процессе открытия решения доставляет ученику наслаждение и воспитывает его эстетически.
   
5. Сюжет задачи и взятые из жизни числовые данные способствует общему развитию ученика.
   

2. Начальная школа есть начало начал образования. Современное начальное математическое образование является частью системы сред­него образования и в то же время своеобразной самостоятельной сту­пенью обучения.

За последние годы начальное математическое образование претерпело ряд изменений, которое связаны прежде всего с изменением целей начального образования, переходом на 4-х летнее начальное образова­ние, появлением вариативности образовательных программ также с введением в 1998г. нового Базисного учебного плана общеобразовательных учреждений РФ.

Для традиционной начальной школы целостно разработаны 3 вариативных курса: (Действует с 1969г.) – «Математика», авт. М.И.Моро и др. (М. Просвещение); «Математика», авт. Питерсон (М. Баласс); «Математика» авт. Истомина, Нефедова (Смоленск: Ассоциация 21 век).

Эти курсы представлены авторскими программами и методическими пособиями для учителя. Традиционный курс Моро существенно обновился. В обновлённых учебниках Моро и др. увеличился объём заданий практического характера; появилось большее разнообразие упражнений; увеличилось количество занимательных упражнений, пробуждающих и развива­ющих интерес к математике; усилена геометрическая линия, способствующая развитию воображения и пространственного мышления.

Обновление содержания повлекло за собой изменение методических подходов к ознакомлению с числами, действиями. Учитываются индивидуаль­ные особенности ребёнка, его жизненный опыт. Появились новые подходы к обучению решению задач. У младших школьников формируются умения читать задачу, выделять условие и вопрос, известные и неизвестные величины, устанавливать взаимосвязи между ними и на этой основе выбирать те ариф­метические действия, выполнение которых позволяет ответить на вопрос задачи. Решение текстовых задач направлено на развитие мышления школь­ников.


3. Для традиционной начальной школы появляются комплекты учебников, построенные на единой концептуальной основе. Одним из таких комплектов является комплект «Начальная школа 21 века», разрабатываемый под редакцией Н.Ф. Виноградовой. (В этот комплект для 1-го класса вхо­дят 5 учебников, 8 рабочих тетрадей и книга для учителя).

Этот курс направлен на обеспечение целостного развития личности ребёнка, его социализацию, становление элементарной культуры деятельности поведения, формирование интеллекта и общей культуры. Именно эти ценности должны стать основой совершенствования процесса начального образования.

Этот комплект обеспечивает достижение необходимых младшему школьнику элементов развития в начальной школе любого типа. Автор­ский коллектив предлагает технологию дифференциального обучения в разнородном классе, все задания по всем предметам разноуровневые, позволяющие не потерять, не затормозить развитие сильных учащихся и помочь слабым преодолеть трудности учения.

Уже много лет успешно используются в начальной школе учебники-тетради «Математика», авторы Жикалкина, Бредихина (с 1993г.)

В настоящее время разрабатываются ещё несколько курсов. Но авто­ры всех вариативных программ для начальной школы обеспечивают выпол­нение обязательного минимума содержания, расширяя и углубляя его.


4. В настоящее время появляются различные типы школ, в которых вводятся альтернативные программы и учебники.

Наиболее распространенной среди альтернативных систем является дидактическая система Л.В. Занкова, направленная на достижение высокого уровня общего развития школьников. Автор учебников И.Н. Аргинская.

Обучение детей предусмотрено с 7-летнего возраста (т.е. 3-х летнее обучение) с 1991/92 учебного года стала необходимость создания новой 4-х летней модели начального обучения в системе Занкова, сохранившей все достижения этой системы и одновременно учитывающей специфику создаваемой новой модели.

Эту систему учителя выбирают потому, что она привлекает своими принципами:

– обучение должно вестись на высоком уровне трудности, в быстром тем­пе;

– ведущая роль отводится теории, причём теоретические знания тесно связаны с обязательным осознанием учащимися процесса обучения.

В этом курсе как и в других – текстовые задачи являются важным разделом. Однако подход к задачам и формированию умения их решать в нём существенно другой. Это выражается прежде всего в отсутствии стремле­ния к ранней типизации задач. Ученики становятся в условия, когда зада­чи решаются не на основе их соотнесения с ранее решенными, а на основе распутывания той жизненной ситуации, которая отражена в конкретной задаче, и перевода её на язык математических отношений.

В трёхлетней школе работа над задачей начинается в феврале 1кл., а в 4-х летней – только во 2-м классе, 1-й класс занимает подготови­тельный период.

Для формирования истинного умения решать задачи ученики прежде всего должны научиться работать с текстом: определять явля­ется ли данный текст задачей, т.е. выделить в нём основные признаки этого вида заданий и его основные элементы, установить между ними связи, определить количество действий, выбрать действия и их поря­док, обосновав свой выбор. Именно эти вопросы образуют одну из двух основных линий работы с задачами в данной системе.

Вторая линия посвящена различным преобразованиям предлагае­мых текстов – как задач, так и не являющиеся ими. Дети превращают тексты – не задачи – в задачи, усложняют и упрощают данные задачи, наб­людают за изменениями в решении, которые возникают в результате са­мых разных преобразований текста задачи.

Алгебраический метод решения задач вводится с 1 класса (со 2 кл. (1-4) и уже к 3 классу становится основным методом решения. Как известно, алгебраический метод развивает теоретическое мышление, спо­собствует к обобщению, формирует абстрактное мышление и, кроме того, обладает такими преимуществами, как краткость записи и рассуждений при составлении уравнений, экономит время. Видимо, эти преимущества и привели к тому, что значительная часть учителей отдаёт предпочтение при решении задач алгебраическому методу.

Однако существует и другое мнение о том, что арифметический ме­тод решения задач развивает мышление не в меньшей степени, т.к. уче­нику необходимо разбить составную задачу на простые и на основе ло­гически строгих рассуждений в определенной последовательности решить их. Арифметический способ решения требует большего умственного напряжения, что положительно сказывается на развитии умственных способностей, математической интуиции, на формирование умения предвидеть реальную жизненную ситуацию.

Именно поэтому арифметический метод решения задач должен быть если не ведущим, то хотя бы полноправным методом решения задач в начальной школе.


5. Рассмотрим формирование умения решать задачи по традиционной системе обучения, в том числе и с использованием новых подходов в обучении.

(Введение задач: Моро (1-4) с.55 1кл.

Истомина (1-3) с.140 1кл.)

Задачи предлагаются с целью понимания математических знаний, приобретения умений логически рассуждать, делать умозаключения, для совершенствования и закрепления навыков.

Решаются и воспитательные цепи: любовь к родному краю, раз­виваем настойчивость, воспитываем волю, связь с жизнью, способст­вуют общему развитию ученика.


а) Подготовительная работа.

М.И. Моро: ознакомление со сложением и вычитанием, построение отрезков,

оперирование со множествами, составление текстов по рис., выполнение схематических рис., составление примеров по ним; всё это учит логически мыслить, развивать воображение, рассуждать.

Н.Б. Истомина: формирование навыка чтения, смысл арифметических действий – сложения и вычитания, отношения: «больше на…», «меньше на…», «увеличить на…», «уменьшить на...», «на сколько б.», «на сколько м.»; предметные действия для разъяснения действий сложения и вычитания, записи математических предложений, составление схематической и символической моделей, разбор текстов. Формируется представление о схеме.

№ 234 На 1 ветке – 14 птичек, а на 2 – на 5 птичек меньше. Обозначь каждую птичку кругом и покажи сколько птичек на 2 ветках. Покажи сколько птичек на двух ветках.



ΟΟΟΟΟΟΟΟΟ Ө Ө Ө Ө Ө




ΟΟΟΟΟΟΟΟΟ


№ 232 От проволоки длиной 14см отрезали часть длиной 5см. Сделай чертёж и покажи ту часть проволоки, которая осталась.


5см






14см


№ 248 В корзине 15 грибов. Из них 5 белых, остальные – лисички. Обозначить все грибы кругами и покажи, сколько в корзине лисичек.





Маша: ΟΟΟΟΟ ΟΟΟΟΟΟΟΟΟΟ


лисички




Миша: ΟΟΟΟΟΟΟΟΟΟΟΟΟΟΟ ΟΟΟΟΟ

лисички


Кто выполнил задание верно?


б) Рассмотрим обучение решению задач и моделирование.

Глубина и значимость открытий, которые делает младший школьник, решая задачи, определяется характером осуществляемой им деятельности и мерой её освоения, тем, какими средствами этой деятельности он владеет. Для того чтобы ученик мог выделить и освоить способ решения широкого класса задач, и не ограничивался нахождением ответа в дан­ной, конкретной, задаче, он должен овладеть некоторыми теоретическими знаниями о задаче и, прежде всего, о её структуре. В структуре любой задачи выделяют:

1. Предметную область, т.е. те объекты, о которых идёт речь в задаче.

2. Отношения, которые связывают объекты предметной области.

3. Требование задачи.

Объекты задачи и отношения между ними составляют условие задачи. Например, в задаче: «Лида нарисовала 5 домиков, а Вова – на 4 домика больше. Сколько домиков нарисовал Вова? – объектами являются:

1) количество домиков, нарисованных Лидой (это известный объект в задаче) 2) количество домиков, нарисованных Вовой (это неизвестный объект в задаче и согласно требованию искомый).

Связывает объекты отношение «больше на».

Работа, проведённая на подготовительном этапе к знакомству с текстовой задачей, позволяет организовать деятельность учащихся, направленную на усвоение её структуры и на осознание процесса её решения.

При этом существенным является не отработка умения решать определенные типы (виды) текстовых задач, а приобретение учащимися опыта в семантическом (смысловом) и математическом анализе различных текстовых конструкций задач и формирование умения представлять их в виде схематических и символических моделей.

В свою очередь, схематические модели бывают вещественными (они обеспечивают графическое действие). К графическим моделям относятся рисунок, условный рисунок, чертёж, семантический чертеж (схему). Так для предыдущей задачи, графическая модель может быть выполнена в виде рисунка:


Л. Δ Δ Δ Δ Δ

В. Δ Δ Δ Δ Δ Δ Δ Δ Δ

?


в виде условного рис.


Л. Ο Ο Ο Ο Ο

В. ڤ ڤ ڤ ڤ ڤ ڤ ڤ ڤ ڤ

?


в виде чертежа


5 д.

Л.

4 д.

В.

?

в виде схематического чертежа (схемы)

Л.

4 д.

В.

?

Модель может выполняться на естественном языке (в словесной форме) я на математическом (символы).

Рассмотрим модель на естественном языке – это общеизвестная краткая запись.

Л. – 5д.

В. – ? на 4 д. б.

Знакомая модель данной задачи, выполненная на математическом языке, имеет вид выражения 5+4.

Таким o6paзoм, чтобы решить задачу надо построить её математическую модель, но помочь в этом могут другие модели, вспомогатель­ные.

Уровень овладения моделированием определяет успех решающего. Поэтому обучение моделированию должно занимать особое и главное место в формировании умения решать задачи. Психологи и многие мате­матики рассматривают процесс решения задачи как процесс поиска системы моделей. Каждая модель выступает как одна из форм отображения структуры задачи, а преобразование её идёт по пути постепенного обоб­щения, абстрагирования и, в конечном результате, построения её мате­матической модели. Освоение моделей – это трудная работа для учащих­ся, поэтому обучение моделированию необходимо вести целенаправленно. (Естественно, что обычная, традиционно применяемая наглядность облег­чает ученику выполнение заданий, но, как показывает школьная практика, её эффективность мала.) (Задачи решаются с опорой на построение моде­лей по программе Истоминой),

Чтобы самостоятельно научиться решать задачи, ученик должен освоить различные виды моделей, научиться выбирать модель соответствующую предложенной задаче и переходить от одной модели к другой.

Рассмотрим с этих позиций методику обучения моделированию при решении задач на сложение и вычитание. Главную роль в формирова­нии умения решать такие задачи играет схематический чертеж, т.к.

1) он однозначно отображает структуру задачи на сложение и вычита­ние. Действительно, если величины находятся в отношении целого и частей т.е. нахождение компонентов, то чертеж будет таким:

а в а

или в с ,

с


если величины связаны отношением «больше (меньше) на», то чертеж такой:

а



в




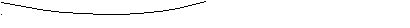
с

В составных задачах рассматриваются различные комбинации этих моделей.

2) схематический чертеж прост для восприятия.

Путь освоения схематического чертежа должен быть постепенным: от рис. к полоскам (как бы закрыли рис., это легче), от них к схеме.


5

5

Δ Δ Δ Δ Δ



Δ Δ Δ Δ Δ Δ Δ

7 7


Рассмотрим упражнение. Имеется несколько кругов разного цвета и диаметра и пары отрезков.


Ο ○ o 1) 2) 3) 4)

o ○ Ο

Ο

○ o


Рассмотрим записи на языке отрезков. О чём они могут рассказать? Какие математические модели могли бы составить? (3 6; 3=3)

а) Под творческой деятельностью учащихся в ходе решения текс­товых задач с использованием моделирования понимается: составление задач по моделям, установление соответствий между содержанием задачи и схематическими рисунками, чертежом; выбор той задачи, которая соответствует рисунку, чертежу; выбор из нескольких схематических рисунков того, который соответствует данной задаче; выбор из данных решений, которое соответствует схематическому рисунку, чертежу; нахож­дение ошибок в рисунках; определение по рисунку, чертежу всех арифметических способов, которыми может быть решена данная задача.

г) При работе над простыми задачами необходимо знакомить уча­щихся с названиями данного вида задач, составлять таблицу задач, решаемых действиями сложения я вычитания.


«+» 1) нахождение суммы «–» 1) нахождение остатка

2) увелич. на неск. единиц 2) уменьш. на неск. единиц

3) нахожд. уменьшаемого 3) сравнение величин

4) нахожд. слагаемого

5) нахожд. Вычитаемого


Формирование умения записывать кратко простую задачу – необходимый элемент в обучении решению простых задач и подготовительный этап к ознакомлению с задачами в два действия. Для этой

цели используются опоры-таблицы. В дальнейшем используем их в устном счёте для решения: задач, составление задач по таблице, сравнение опор позволяет выявить отличительные признаки задач, позволяют разъяснить взаимосвязь представленных задач, преобразовывать их из одной в дру­гую, помогают предупредить смешение задач. Используются такие опоры-перфокарты:


Было –

–

? Стало –


(Затем также на умножение и деление).

Теперь появляется возможность сравнивать и сопоставлять пары задач, чётко выделяя их существенные признаки, сходство и различия между ними, выполнять проверку (соотнесением, составлением обратных, прикид­кой).

В конце изучения темы «Сложение и вычитание в 100» проводятся обобщающие уроки по действиям. Формирование умения решать простые задачи получает дальнейшее развитие и доводится до совершенства в сознании каждого ученика.

Особое место в формировании умения решать задачи отводятся умению находить разные методы, приёмы, способы решения. Решение задачи по-разному – мощное средство постижения мира, осознания разнообразия свойств и отношений его элементов. Разные методы и способы решения – это средство развития познавательного интереса, умения отстаивать свою точку зрения, способности слышать и понимать других людей.

Решение задач нельзя считать самоцелью, в них следует видеть средство к углубленному изучению теоретических положений и вместе с тем средство развития мышления, путь осознания окружающей действительности, тропинку к пониманию мира.

Умение решать задачи – это одно из сложнейших умений. Формируя его, важны все этапы работы с задачей: чтение и понимание текста, вдумчивое рассмотрение содержания и ситуации, лежащей в основе задачи, краткая запись задачи и иллюстрация, установление связей и за­висимостей между данными и искомыми, расчленение составной задачи на простые, выбор действия, установление последовательности в действиях, вычисления и проверка решения.

Основное методическое правило при обучении решению задач: не спешить переходить к решению новой задачи, пока не исчерпаны все или почти все заложенные в ней возможности к развитию мыслительных способностей ученика. Это правило надо всегда помнить и неизменно им руководствоваться.


6. ТЕОРЕТИКО-МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ПОИСКА СПОСОБОВ РЕШЕНИЯ ЗАДАЧ.


Каждая задача – это единство условия и вопроса. Связь между условием и вопросом может быть прямой и косвенной, они влияют на поиск решения.

Прямая связь: ориентирует на использование того, что дано в условии, для ответа на него.

Задача: (№ 253 «М-3»)

«Две бригады покрывали асфальтом шоссе. Одна бригада заасфальтировала 5км, другая на 2км 200м б. После этого осталось заасфальтировать 800м шоссе. Какой длины участок надо было заасфальтировать?

Вопрос дан в прямой форме, вопрос непосредственно направляет на использование данных для ответа на него, показывает ход мыслительного процесса.

Косвенная связь: вопрос надо преобразовать, что может определить разные способы решения.


1) Переформулировка вопроса.

Задача: (№ 517)

«Два отряда школьников вышли одновременно навстречу друг другу из двух поселков. Один отряд шёл со скоростью 4км/ч, другой – 3км/ч. Встреча произошла через 2ч. Найти расстояние между посёлками.


1) какое расстояние прошли оба отряда?

4 · 2 + 3 · 2 = 14 (км)

2) какое расстояние пройдут оба отряда за 2ч, двигаясь с указанной скоростью?

(4 + 3) · 2 = 14 (км)


2) Подбор вспомогательного вопроса (неравносильной данному).

Задача (№ 525)

На сах. завод привезли в первый день 633т 600кг свеклы, во второй день в 2р м. Сколько сахара получилось из всей свеклы, если сахар составляет 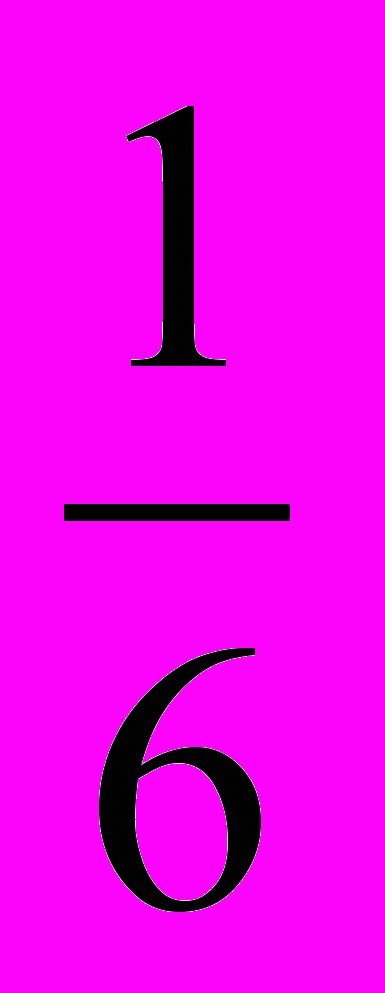массы свеклы?

1 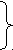– 633т 600кг

2 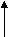– ? в 2р м.

Сахар – ?, 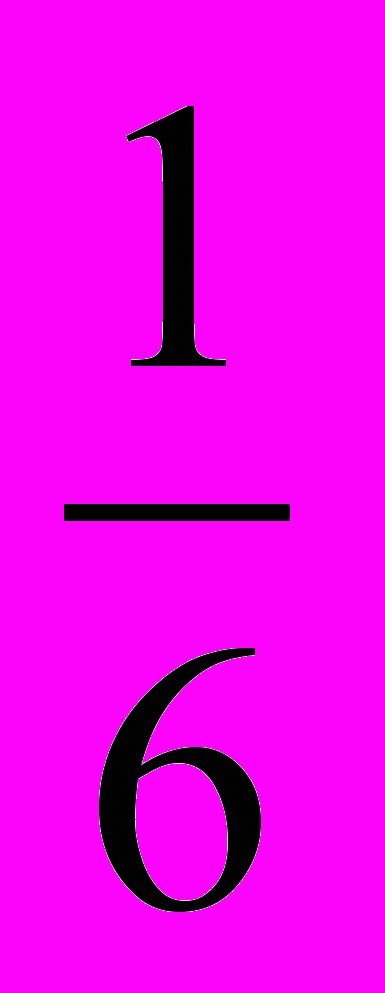всей массы свеклы


1.

1) 633600 : 2 = 316800 (кг) – II

2) 633600 + 316800 = 950400 (кг) – привезли всего

3) 950400 : 6 = 158400 (кг) – сахар


2. I




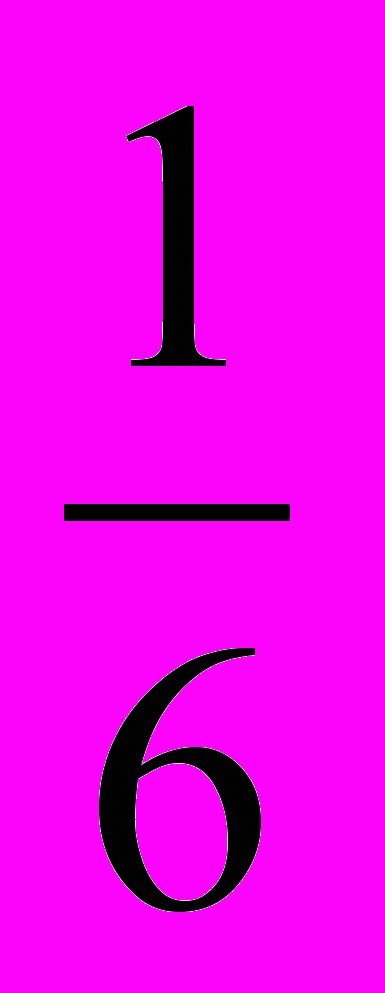
II


1) 633600 : 2 = 316800 (кг)

2) 316800 · З = 950400 (кг)

3) 950400 : 6 = 158400 (кг)


3.

1) 633600 : 2 = 316800 (кг)

2) 316800 : 6 = 52800 (кг)

3) 52800 · 3 = 158400 (кг)


4.

1) 633600 : 2 = 316800 (кг)

2) 633600 + 316800 = 950400 (кг)

3) 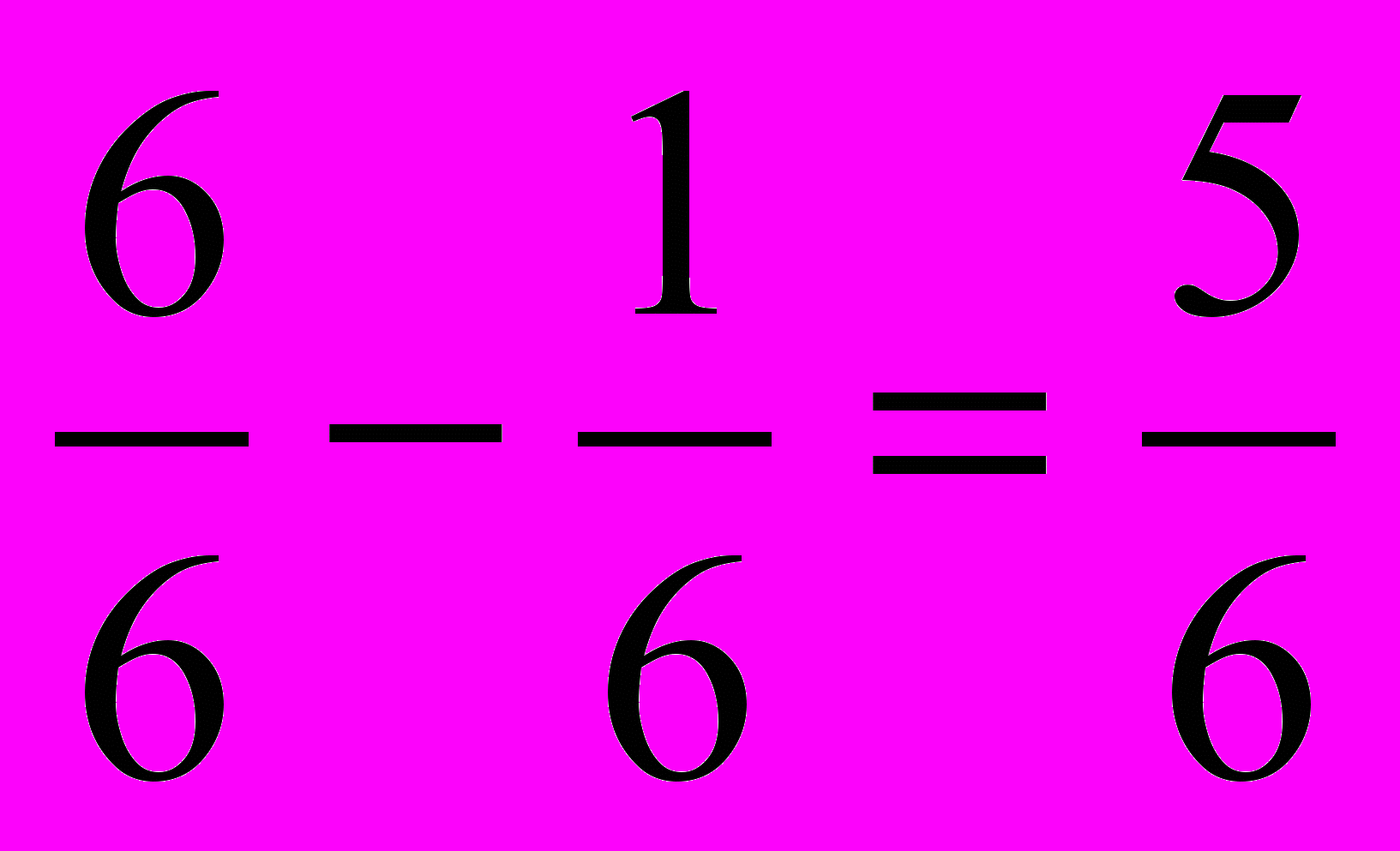– отходы от всей свеклы

4) 950400 : 6 · 5 = 792000 (кг) – отходы

5) 950400 – 792000 = 158400 (кг) и др.

Задача: (№ 642)

«В парке посадили 5 рядов клёнов, по 16 шт. в каждом ряду, и столько же лип, но по 20 шт. в ряду. Сколько рядов лип посадили?

1) Что нужно предварительно узнать, чтобы ответить на вопрос? – один ход мыслительного процесса.

(16 · 5) : 20 = 4 (р.)

2) Каких рядов будет больше? (клёнов)

Почему? (их меньше в каждом ряду)

на 20 – 16 = 4

4 «меньше» липы, повторенные 4 раза, дадут 16, т.e. число клёнов в 1р, значит рядов лип на 1 меньше, т.е. 5 – 1 = 4 (р.)


Задача: За 7 дней столовая израсходовала 35кг масла. На сколько дней хватит при той же норме расхода 105кг?


Здесь логическая основа в двух уровнях – открытом и скрытом.


1. 1) 35 : 7 = 5 (кг) 2. 1) 105 : 35 = 3 (р.)

2) 105: 5= 21(д.) 2) 7 · 3 = 21 (д.)


Задача: Красная Шапочка пригласила в гости Белоснежку и 7 гномов. Для угощения она приготовила 6 апельсинов и 5 яблок. Два фрукта она отложила. Хватит ли гостям оставшихся фруктов?


1. 1) 6 + 5 = 11 (ф.) 2. используем наглядное преставление:

2) 11 – 2 = 9 (ф.) Δ Δ Δ Δ Δ ΔΟΟΟΟΟ

3) 9 8 – хватит 6 + (5 –2) = 9

(6 – 2) + 5 = 9

(6 – 1) + (5 – 1) = 9


РЕШЕНИЕ ЗАДАЧ РАЗНЫМИ СПОСОБАМИ.


При работе над составными задачами необходимо более широкое и активное включение детей в решение задач различными способами. В практике большинство учителей мало уделяют вниманию решению задач разными способами и не понимают, какие большие возможности таятся в этом. Начинать эту работу надо с 1 класса, как ввели состав­ную задачу.

1. «Дети нашли 10 грибов, потом ещё 8 грибов. Один гриб оказался несъедобным. Сколько у детей съедобных грибов?»

1 (10 + 8) – 1 = 17 (гр.) Отыскивание этих способов

2 (10 – 1) + 8 = 117 (гр.) помогает детям игровая ситуация;

3 10 + (8 – 1) =17 (гр.) схематический чертеж.


2. «Дети посади ли 4р. яблонь по 12 штук в каждом, 2 ряда слив по 18 деревьев. Сколько всего деревьев посадили дети?»


1. 1) 12 · 4 = 48 (ябл.) 2. 1) 4 + 2 = 6 (р.) 3. 1) 18 · 6 = 108 (дер.)

2) 18 · 2 = 36 (сл.) 2) 12 · 6 = 72 (дер.) 2) 6 · 4 = 24 (дер.)

3) 49 + 36 = 84 (дер.) 3) 18 – 12 = 6 (дер.) 3) 108 – 24 = 84 (дер.)

4) 6 · 2 = 12 (дер.)

5) 72 + 12 = 94 (дер.)


ΟΟΟΟΟΟΟΟΟΟΟΟCC I, II, III – по горизонт.

ΟΟΟΟΟΟΟΟΟΟΟΟCC

ΟΟΟΟΟΟΟΟΟΟΟΟCC

ΟΟΟΟΟΟΟΟΟΟΟΟCC

ΟΟΟΟΟΟΟΟΟΟΟΟΟΟ ΟΟΟΟ

ΟΟΟΟΟΟΟΟΟΟΟΟΟΟ ΟΟΟΟ


4. 1) 4 + 2 = 6 (д.) 5. 1) 18 – 12 = 6 (д.) 4. 1) 18 – 4 = 14 (д.)

2) 8 · 12 = 72 (д.) 2) 6 · 2 = 12 (д.) – ещё один ряд 2) 4 + 2 = 6 (р.)

3) 2 · 6 = 12 (д.) 3) 4 + 2 + 1 = 7 (р.) 3) 14 · 6=84 (дер.)

4) 72 + 12 =84 (д.) 4) 12 · 7 = 34 (д.)


Похож на 2, но смысл другой.

Какие-то способы можно решить в классе на уроке, другие на кружковой работе.

Найти другой способ позволяет: свойство арифметических действий; приём уравнивания или изменения задачи; приём дополнения условия, приём представления ситуации и мыс­ленное практическое решение; другой вид разбора и т.д. Тем самым спо­собные дети получают поистине неограниченные возможности в отыскании всё новых и новых способов решения, глубже усваивая математичес­кие зависимости, свойства. Но стремление детьми решить задачу различными способами не должно быть безумной манипуляцией с числами, они должны вдумчиво вчитываться в содержание задачи, выделять все взаимосвя­зи, на которые раньше не обращали внимание.

Существуют различные модели задач, чаще всего удачно вобранная схема, по которым можно найти различные способы решения.


3. «Саша сделал 3 корабликов, а Миша – на 4 кораблика больше. Сколько всего корабликов сделали мальчики?




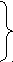
С – 6 к.

?

М – ? на 4 к. б.





С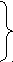. 6 к.

на 4 к. б. ?

М.


1. 1) 6 + 4 = 10 (к.) 2. 1) 6 + 6 = 12 (к.) 3. 1) 6 + 4 = 10 (к.)

2) 6 + 10 = 16 (к.) 2) 12 + 4 = 16 (к.) 2) 10 + 10 = 20 (к.)

3) 20 – 4 = 16 (к.)


4. 1) 4 – 2 = 2 (к.)

2) 6 + 2 = 3 (к.)

3) 8 + 8 = 16 (к.)


Можно давать такие задания домой, затем без напоминания будут искать различные способы решения.


4. Задача аналогичная 1.

«Девочка нашла З грибов, мальчик – 23. Среди чих 6 оказалось несъедобными. Сколько съедобных грибов нашли?


1) (36 + 28) – 6 = 58 (гp.) 5) (36 – 5) + (28 – 1)

2) (36 – 6) = 58 (гр.) 6) (36 – 2) + (28 – 4)

3) 36 + (28 – 6) = 58 (гр.) 7) (36 – 4) + (28 – 2)

4) (36 – 1) + (28 – 5) 8) (36 – 3) + (28 – 3)

Ответ: 58 грибов.

5. Задача «Один теплоход за 8ч прошёл 312км. За сколько часов пройдёт второй теплоход 231км, если его скорость на 6км/ч меньше?».
   

v t s

1 ? Зч 312км

2 ? на 6км/ч м. ? 231км


1. 1) 312 : 8 = 39 (км/ч) 2. 1) 6 · 8 = 48 (км)

2) 39 – 6 = 33 (км/ч) 2) 312 – 48 = 264 (км)

3) 231 : 33 = 7 (ч) 3) 264 : 8 = 33 (км/ч)

4) 231 : 33 =7 (ч)


3. 1) 312 : 8 = 39 (км/ч)

2) 39 – 6 = 33 (км/ч)

3) 6 · 8 = 48 (км)

4) 312 – 48 = 264 (км)

5) 263 – 231= 331 (км) – 1ч

6) 8 – 1 = 7 (ч)

Ответ: 7 часов.


6. «В зале 8 рядов по 12 стульев. В зал пришли ученики из 2-х классов по 42 ученика. Хватит ли стульев? Если хватит, сколько останется?»


1. 1) 12 · 8 = 96 (ст.) 2. 1) 12 · 8 = 96 (ст.)

2) 42 · 2 = 84 (уч.) 2) 96 – 42 = 54 (ст.)

96 84 – хватит 3) 54 – 42 = 12 (ст.)

3) 96 – 84 = 12 (ст.)


3. 1) 42 · 2 = 84 (уч.) 4. 1) 12 · 8 = 96 (cт.)

2) 84 : 2 = 7 (13.) 2) 96 : 2 = 48 (cт.)

3) 8 – 7 = 1 (р.) – 12 ст. 3) 48 – 42 = 6 (ст.)

4) 6 · 2 = 12 (ст.)


5. 1) 42 : 12 = 3 (ост.6) – Зр. и 6 мест. 1) 42 : 12 = 3 (ост.6)

2) 12 – 6 = 6 (ст.) – ост. 2) 42 + 6 = 48 (уч.)

3) 42 – 6 = 36 (ст.) 3) 48 : 12 = 4 (р.)

4) 36 : 12 = 3 (р.) 4) 3 + 4 = 7 (р.)

5) 3 + 1 + 3 = 7 (p.) 5) 8 – 7 =1 (p.) – 12 ст.

6) 8 – 7 = 1 (р.) – 12 ст.


7. 1) 8 : 2 = 4 (р.) – каждому классу 3. 1) 42 · 2 = 84 (уч.)

2) 12 · 4 = 48 (ст.) 2) 84 : 8 = 10 (ост.4) – 10 уч. в 1р. и

3) 48 – 42 = 6 (ст.) – своб. 4 уч. ост.

4) 6 · 2 = 12 (ст.) 3) 12 – 10 = 2 (ст.) – своб.

4) 2 · 8 = 16 (ст.) – своб.

5) 16 – 4 = 12 (ст.)


9. 1) 12 · 8 = 96 (ст.)

2) 96 : 42 = 2 кл. (12 – ост.)

10. 1) 12 : 2 = 6 (ст.) – по 6 ст. выд. кажд. кл. в 1р.

2) 42 : 6 = 7 (p.) – займёт каждый класс

3) 8 – 7 = 1 (р.) – 12 ст.

0твет: хватит; 12 стульев.


Графические схемы имеют преимущество, т.к. в отражаются количественные отношения между величинами, о которых говорится в задачах, показываются связи между данными и искомыми, т.е. схемы де­лают математические связи и зависимости наглядными для учеников, помогают выделить главное в каждом этапе и выбрать действие для решения простой задачи, решаемой на конкретном этапе. По традицион­ной программе мало используется схем для решения задач: даётся толь­ко общее представление о них З кл. (1-4) № 1 (с. 41) и, конечно, в за­дачах на движение.


Таким образом, использование предметного и графического моделирования обеспечит более качественный анализ задачи, осоз­нанный поиск решения её, обоснованный выбор необходимого арифметического действия, поможет найти рациональный способ решения задачи, организовать творческие задания по преобразованию задач, по установлению условий, при которых задача не имеет решения, поможет обобщить знания, организовать индивидуальный подход при обучении решению текстовых задач.

Мы должны сформировать у учащихся общие умения решать задачи. Обнаружить это умение можно при предъявлении ученику незнакомой задачи. Если ученик сразу отказывается от её решения: «мы такие не решали», значит, общее умение не сформировано. Если же ученик начинает преобразовывать задачу, используя различные общие приёмы и либо находит ответ, либо делает вывод, что задачу решить не может, т.к, не знает какой-либо зависимости, не владеет какой-то информацией, то он владеет общим умением.

В условиях развивающего обучения необходима широкая вариация заданий, так как она включает учащихся в поисковую деятельность.


В портфеле 14 тетрадей. Из них 9 в клетку. Остальные в линейку. Сколько тетрадей в линейку лежит в портфеле?


1. Выбор схемы.


9т ?

Маша


14т


?




Миша


14т 9т


Кто из них невнимательно читал текст задачи?


2. Выбор вопросов


От проволоки длиной 15 дм отрезали сначала 2дм, потом ещё 4 дм. Подумай на какие вопросы можно ответить, пользуясь этим условием:

а) Сколько всего дм проволоки отрезай?

б) На сколько дм меньше отрезали в 1-й раз, чем во 2-й?

в) На сколько дм проволока стала короче?

г) Сколько дм проволоки осталось?


3. Выбор выражений.


На велогонках стартовало 70 спортсменов. На 1-м этапе сошли 4 велосипедиста, на втором – 6. Сколько спортсменов пришло к финишу?


Выбери выражение, которое является решением задачи.


6 + 4 6 – 4 70 – 6

70 – 6 – 4 70 – 4 – 8 70 – 4


4. Выбор условия к данному вопросу.


Подбери условия к данному вопросу и реши.

Сколько всего детей занималось в студии?

а) В студии 30 детей, из них 16 мальчиков.

б) В студии мальчики и девочки. Мальчиков на 7м., чем девочек.

в/ В студии 8 мальчиков и 20 девочек.

г/ В студии 8 мальчиков а девочек на 2б.

д/ В студии занималось 8 мальчиков, а девочек на 2м.


5. Выбор данных


На аэродроме было 75 самолетов. Сколько самолетов осталось?


Выбери данные, которыми можно дополнить условие задачи, чтобы ответить на поставленный вопрос:


а) Утром прилетело 10 самолётов, а вечером улетело 30.

б) Улетело на 20 самолетов б., чем было.

в) Улетело сначала 30 самолётов, а потом 20.


6. Изменение текста задачи в соответствии с данным решением.

Подумай! Что нужно изменить в текстах задач, чтобы выражение (9–6) было решением каждой?


а) На двух скамейках сидели 6 девочек. На одной из них 9.

Сколько девочек сидело на 2-й скамейке?

б) В саду 9 кустов красной смородины, а кустов чёрной смородины на 6 б. Сколько кустов чёрной смородины?

в) В гараже 9 легковых машин и 6 грузовых. Сколько всего машин в гараже? Сколько всего машин в гараже?


7. Объяснение выражения, составление по данному условию.


Дано условие и несколько выражений надо пояснить каждое.


Коля выше Пети на 20см, а Петя выше Вовы на 7см. Рассмотри схему, и подумай, на какой вопрос можно ответить, пользуясь данным условием.


7. Постановка вопроса, соответствующего данной схеме.


20см

К.


7см

П.


В.


Курица легче зайца на 4кг, а заяц легче собаки на 8кг. На сколько собака тяжелее курицы? На сколько курица легче собаки?

9. Выбор решения задачи.


К.


4кг

З.

8кг




С.


Маша: 4 + 8 = 12 (кг)

Миша: 8 – 4 = 4 (кг)


Кто прав?