Элективный курс по математике

Вид материала

Элективный курс

Содержание Содержание курса Критерии эффективности и реализации программы. Библиографический список 1.Вводное занятие. Вводный тест 2. История сюжетных задач. Сюжетные задачи древних народов. Старинные методы решения сюжетных задач. Задача 3. (Магницкого). 3.Виды сюжетных задач. Анализ структуры сюжетных задач. Установите в каждой из следующих задач, какие величины и какие их значения заданы явно и неявно, каков характер каждого из этих Установите тип соотношения, характеризующего описанного в задаче явления. Решить задачи 4.Виды сюжетных задач. Анализ структуры сюжетных задач. Решить задачи методом Ньютона Метод Декарта Метод решения задач с неопределенными неизвестными 5. Графическое решение сюжетных задач.

Подобный материал:

• Элективный курс. «Углубленное изучение некоторых вопросов математики», 64.95kb.
• Элективный курс. «Подготовка к егэ. Решение заданий поля С.» 11 класс, 34 часа, 55.92kb.
• Элективный курс по математике для 11 класса «Решение задач повышенной сложности», 109.29kb.
• Элективный курс «глобальные проблемы человечества», 121.74kb.
• В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
• Элективный курс по астрономии, 93.86kb.
• Пояснительная записка Элективный курс «Природа тел Солнечной системы» предназначен, 50.52kb.
• Ф. В. Чижова методическая разработка элективный курс, 490.04kb.
• Элективный курс «Методы решения задач по физике» 10 11 классы 68 часов, 115.81kb.
• Элективный курс по математике «Уравнения и неравенства» учитель: Пономарёва, 19.19kb.

ЭЛЕКТИВНЫЙ КУРС ПО МАТЕМАТИКЕ
«РЕШЕНИЕ СЮЖЕТНЫХ ЗАДАЧ»


Авдонина Надежда Валерьевна , учитель математики МОУ СОШ № 2 п. Спирово.

Сюжетные задачи – это наиболее древний вид школьных задач. Они всегда широко использовались, и будут использоваться в обучении математике. Они помогают учащимся понять сущность и методику применения математического моделирования, сформировать общий подход к решению любых задач, однако в школьном курсе математики отводится недостаточно времени решению сюжетных (текстовых) задач.

Психологические исследования проблемы обучения решению задач показывают, что основные причины несформированности у учащихся общих умений и способностей в решении задач состоят в том, что школьникам не даются необходимые знания о сущности задач и их решений, а поэтому они решают задачи, не осознавая должным образом свою собственную деятельность. У учащихся не вырабатываются отдельно умения и навыки в действиях, входящих в общую деятельность по решению задач, и поэтому им приходится осваивать эти действия в самом процессе решения задач, что многим школьникам не под силу. Не стимулируется постоянный анализ учащимися своей деятельности по решению задач и выделению в них общих подходов и методов, их теоретического осмысления и обоснования.

Кроме того, текстовые задачи включены в экзаменационные работы как в 9, так и в 11 классах.

Это и определило необходимость в составлении данного курса.

Цель курса:

Создание условий для овладения навыками математического моделирования при решении сюжетных задач.

Задачи курса:

• конкретизировать понятие «сюжетная задача»;
  
• ознакомить учащихся с видами математической модели сюжетной задачи;
  
• ознакомить учащихся с всевозможными подходами к решению сюжетных задач различного уровня сложности.
  

Учебный процесс элективного курса предусматривает следующие методы и формы работы:

• изложение нового материала учителем в форме лекции;
  
• дифференцированный подход на практических занятиях: для всех тем курса подобраны задания различного уровня сложности;
  
• самостоятельная работа с учебной литературой;
  
• выбор тем для рефератов;
  
• индивидуальные консультации.
  

Данный элективный курс предназначен для учащихся 9 классов. На его изучение отводится 17 часов.

Содержание курса

В программу элективного курса включены следующие темы и ориентировочное время для их изучения:

№№ п/п	Тема	Количество часов
1.	Вводное занятие.	1
2.	История сюжетных задач. Сюжетные задачи древних народов. Старинные методы решения сюжетных задач.	2
3.	Виды сюжетных задач. Анализ структуры сюжетных задач.	2
4.	Построение алгебраической модели сложных открытых и замкнутых задач.	7
5.	Графическое решение сюжетных задач.	3
6.	Заключительная часть	2

Методические рекомендации

1. Вводное занятие.
   

На вводном занятии рекомендуется:

• объяснить учащимся цели данного элективного курса;
  
• поставить необходимые задачи;
  
• рассказать кратко о том, что будет изучаться, выяснить всевозможное применение задач в жизнедеятельности человека (с помощью учащихся);
  
• рассказать о требованиях к подготовке и защите рефератов;
  
• объяснить, каким образом будут подводиться итоги изучения курса и оцениваться работа учащихся.
  

2. История сюжетных задач. Сюжетные задачи древних народов. Старинные методы решения сюжетных задач.
   

Знать:

• историю сюжетных задач;
  

• старинные методы решения сюжетных задач.
  

Уметь:

применять при решении старинных задач:

• способ пропорционального изменения;
  
• способ пропорционального деления;
  
• деление в разностном отношении;
  
• метод «одного ложного положения»;
  
• метод «двух ложных положений»;
  
• правило обращения.
  

Основное содержание:

• подготовительный этап – актуализация базовых знаний и умений, вводный математический тест с самопроверкой;
  
• демонстрация старинных способов решения сюжетных задач на характерных приемах;
  
• решение задач данными способами.
  

3. Виды сюжетных задач. Анализ структуры сюжетных задач.
   

Знать:

виды сюжетных задач и анализ структуры задач на:

• на движение;
  
• на совместную работу;
  
• на зависимость между компонентами арифметических действий;
  
• на проценты;
  
• на планирование.
  

Уметь:

• выявить объект задачи (предмет, явление, событие, процесс);
  

установить:

• какие величины характеризуют количественную ситуацию задачи;
  
• какие моменты (случаи, эпизоды) рассматриваются в задаче;
  
• какие величины и какие их значения заданы явно и неявно, каков характер каждого из этих значений;
  
• тип соотношения, характеризующий описанное в задаче явление.
  

Основное содержание:

Рассмотреть главные способы анализа структуры и состава сюжетных задач:

• выявление объекта задачи;
  
• анализ характеристики объектов сюжетных задач;
  
• установление значений величин, заданных в задаче;
  
• соотношения между значениями величин.
  

4. Построение алгебраической модели сложных открытых и замкнутых задач.
   

Знать:

• Понятие замкнутой и открытой задачи;
  
• Основные приемы составления уравнений для решения задач
  

Уметь:

• Строить для задачи алгебраическую модель в виде уравнения или систем уравнений.
  
• Строить алгебраические модели сложных задач;
  

Основное содержание:

Решение задач с помощью составления уравнения:

• методом Ньютона;
  
• методом Декарта;
  
• методом одной вспомогательной задачи;
  
• общим методом решения задач с неопределенными неизвестными.
  

5. Графическое решение сюжетных задач.
   

Знать:

• график прямой пропорциональности.
  

Уметь:

• Пользоваться различными прямоугольными системами координат на одном и том же чертеже.
  

Основное содержание:

• Решать задачи графическим способом.
  

6. Заключительная часть.

Демонстрация и защита рефератов.

Критерии эффективности и реализации программы.

Программа может считаться усвоенной учеником, если по каждой теме он решил не менее 60% предложенных задач. Учитель и ученик, по своему усмотрению, могут составить «таблицу успешности», куда вносятся баллы, набранные учеником при выполнении заданий. Причем необходимо учитывать не только те задания, которые решены, верно, и полностью, но и те, в которых ребенок, верно, усмотрел путь решения. Особо отличаются оригинальные способы решения.

Библиографический список

Для учителя

1. Балл Г.А., Чмут Т.К. Разработка заданий развивающего характера на базе сюжетных математических задач. Учебные материалы и учебные ситуации./ Под ред. Г.С.Костюка, Г.А.Балла. Киев, 1988г.
   
2. Башмаков М.И. Уравнения и неравенства. М., 1983 г.
   
3. Бочковская О.Т. Решение задач как средство развития логического мышления. /Под ред. А.С.Пчелко. – М., 1949 г.
   
4. Бронштейн С.С. Методика алгебры. – М., 1985 г.
   
5. Герасименко И.Ф. Составление задач учащимися как способ обучения их умениям применять теоретические знания на практике. Умственное развитие учащихся в процессе обучения. Волгоград, 1967г.
   
6. Семенов Е.М. Развитие логического мышления учащихся в процессе решения арифметических задач. М., 1964 г.
   
7. Турецкий Е.Н. Формирование у учащихся восьмилетней школы навыков алгебраического метода решения текстовых задач. Ташкент, 1968г.
   
8. Фридман Л.М., Левочкина А.Я., Таравкова Л.М. Опыт формирования у учащихся общего подхода к решению текстовых задач. Актуальные психолого-педагогические проблемы обучения и воспитания. М., 1973г
   
9. Фридман.Л.М. Сюжетные задачи по математике. История, теория, методика. – М., Школьная пресса, 2002 г.
   
10. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. М., 1989 г.
    
11. Фридман Л.М. Графическое решение текстовых задач. М., 1958 г.
    

Для учащихся

15. Бочковская О.Т. Решение задач как средство развития логического мышления./ Под ред. А.С.Пчелко. – М., 1949 г.

12. Кострикина Н.П. Задачи повышенной трудности в курсе алгебры 7-9 классов. М., 1991г.
    
13. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. М., «Дрофа», 2000г
    
14. Фридман Л.М. Графическое решение текстовых задач. – М., 1958г.
    

16.Ясиловый А.Г. Составление математических задач учащимся как средство активизации их познавательной деятельности. – Ярославль, 1974 г.


Приложение

Дидактический материал.

Вводный тест состоит из 5 заданий, на выполнение которого отводится 45 минут. Внимательно прочитайте каждое задание и ответы к нему. Выполняйте задания в том порядке, в котором они даны. Если какое-то задание не удается выполнить сразу, переходите к следующему. К пропущенному заданию вы можете вернуться, если останется время.

Все задания оцениваются в 1 балл. Оценка:

«5» - 5 правильных ответов,

«4» - 4 правильных ответа,

«3» - 3 правильных ответа,

«2» - 2 правильных ответа.

Приступайте к работе. Желаем успеха!


1.Вводное занятие. Вводный тест

1. Найти 1/5 от суммы чисел 3 1/8 и 1 1/4

а) ½ б) 7/8 в) 5/6 г) 2/3

2. Клубника содержит 6% сахара. Сколько кг. сахара в 27 кг. клубники?

а) 1,82 кг. б) 1,62 кг. в) 2,24 кг. г) 2,42 кг.

1. Решить систему уравнений и найти значение выражения х² + у²
   

2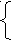х – у = 1

х + у = -4

а) 17 б) 5 в) 13 г) 10

2. На катушке было 210 м. провода. Сначала отрезали 3/5 всего провода, а затем 2/3 остатка. Сколько провода осталось в катушке?
   

а) 56 м. б) 28 м. в) 84 м. г) 10 м.


2х + 1 5х – 2

3 4

-

5. Решить уравнение: =1


а) 3,5 б) 2/7 в) –2/4 г) –3,5

1. Катер прошел 15 км. по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Найдите скорость лодки по течению реки, если скорость течения равна 4 км/ч.
   

а) 12 км/ч. б) 20 км/ч. в) 16 км/ч. г) 32 км/ч.


2. История сюжетных задач. Сюжетные задачи древних народов. Старинные методы решения сюжетных задач.

Решить задачи старинными методами.

1 уровень сложности.

Задача 1. Лесопромышленник заплатил за три лесные дачи поровну; десятина лесу в первой даче обошлась ему 64 руб., во - второй 80 руб., в третьей – 90 руб. Сколько десятин в каждой из этих трех дач, если во всех трех 6780 десятин лесу?

Задача 2. Чайный торговец купил 3 ящика чая, всего 13/4 пуда, и за один ящик заплатили 72 рубля., за второй-66 рублей, за третий –40 рублей. Сколько чая было в каждом ящике, если 1,1 фунта из первого ящика стоили столько, сколько 9/5 фунта из второго, а 20/3 фунта из второго столько же, сколько 11/2 фунта из третьего?

Задача 3. (Магницкого). Спросил некто учителя: «Сколько у тебя в классе учеников, так как хочу отдать к тебе в учение своего сына». Учитель ответил: «Если придет еще столько же учеников, сколько имею, и полстолько и четвертая часть и твой сын, тогда будет у меня учеников 100». Сколько в классе учеников?

2 уровень сложности .

Задача 4. Имеется 9 слитков золота и 11 слитков серебра, их взвесили, вес как раз совпал. Переложили слиток золота и слиток серебра, золото стало легче на 13 ланов. Спрашивается, какой вес слитка золота и слитка серебра каждого в отдельности?

Задача 5. Некий торговец купил 112 баранов, старых и молодых, дал 49 рублев 20 алтын, за старого платил по 15 алтын и по 2 деньги, а за молодого по 10 алтын, и ведательно есть, колико старых и молодых баранов купил он.

Задача 6. Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель поделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели?

3.Виды сюжетных задач. Анализ структуры сюжетных задач.

Задание. Проанализируйте нижеприведенные задачи и укажите для каждой из них:

• что является объектом?
  
• Какие моменты рассматриваются в ней?
  
• Какие величины характеризуют количественную ситуацию задачи?
  

Задача 7. Тракторист по плану должен был ежедневно вспахивать по 15 га земли. Фактически он вспахивал ежедневно на 5 га больше дневной нормы, поэтому за 4 дня до окончания вспашки по плану ему осталось вспахать 40 га. За сколько дней по плану тракторист должен был закончить работу?

Задача 8. Если открыть краны с горячей и холодной водой, то ванна наполнится до требуемого уровня за 8 мин., а если открыть один кран лишь с горячей водой, то ванна наполнится до того же уровня за 18 мин. за сколько минут может, наполнится ванна до того же уровня холодной водой, протекающей через другой кран?

Задача 9. Катер, собственная скорость которого 8 км/час, прошел по реке расстояние, равное 15км, по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 часа.

Установите в каждой из следующих задач, какие величины и какие их значения заданы явно и неявно, каков характер каждого из этих значений.

Задача 10. Зрительный зал клуба имел форму прямоугольника длиной 24,8м. Длину зала увеличили на 2м. за счет подсобных помещений, и тогда площадь увеличилась на 20 кв.м. Найдите первоначальную площадь зала.

Задача 11. Теплоход идет по течению реки со скоростью 26 км/ч, а против течения – со скоростью18 км/ч. За сколько времени он совершит рейс из города А до города В и обратно, если в городе В он стоял под погрузкой 2 часа.

Установите тип соотношения, характеризующего описанного в задаче явления.

Задача 12. Длина садового участка на 10 м. больше его ширины. Его площадь решили увеличить на 400 кв.м. Для этого длину увеличили на 10м., а ширину – на 2м. Найдите площадь нового участка.

Задача 13. Для школьной площадки выделен прямоугольный участок земли определенной площади. Если его заменить квадратным участком той же площади, то потребуется меньше материала для его огораживания. Для этого надо длину участка уменьшить на 12 м, а ширину увеличить на 10 м. Чему равна сторона квадратного участка?

Задача 14. В двух школах поселка было 1500 учащихся. Через год число учащихся первой школы увеличилось на 10%, а второй – на 20%, и в результате общее число учащихся стало равным 1720. Сколько учащихся было в каждой школе первоначально?

Решить задачи:

1 уровень сложности .

Задача 15. Из города А в город В, расстояние между которыми 120 км, выехали одновременно два велосипедиста. Скорость первого на 3 км/ч больше скорости второго, поэтому он прибыл в город В на 2 ч раньше. Определите скорости велосипедистов.

Задача 16. Трое изобретателей получили за свое изобретение премию в размере 1410 р., причем второй получил 1/3 того, что получил первый, и еще 60 р., а третий получил 1/3 денег второго и еще 30 р. Какую премию получил каждый?

Задача 17. Машинистка должна была напечатать за определенное время 200 страниц. Печатая в день на 5 страниц больше, она завершила работу на 2 дня раньше срока. Сколько страниц в день печатала машинистка?

2 уровень сложности .

Задача 18. Из пункта А в пункт В, расстояние между которыми 18 км, одновременно выезжают два велосипедиста. Скорость одного из них на 5 км/ч меньше скорости другого. Велосипедист, который первым прибыл в В, сразу же повернул обратно и встретил другого велосипедиста через 1 ч 20 мин. после выезда из А. На каком расстоянии от пункта В произошла встреча?

Задача 19. Два мастера, работая вместе, могут выполнить заказ за 6 ч. Если первый мастер будет работать 9 ч, а потом его сменит второй, то он закончит работу через 4 ч. За сколько времени может выполнить заказ каждый из мастеров, работая отдельно?

Задача 20. Турист проехал расстояние между двумя городами за 3 дня. В первый день он проехал 1/5 всего пути и еще 60 км, во второй ¼ всего пути и еще 20 км и в третий день 23/80 всего пути и оставшиеся 25 км. Найти расстояние между городами.

Задача 21. Цену товара сперва снизили на 20%, затем новую цену снизили еще на 15% и, наконец, после перерасчета произвели снижение еще на 10%. На сколько процентов всего снизили первоначальную цену товара?

Задача 22. Швея получила заказ сшить 60 сумок к определенному сроку. Она шила в день на 2 сумки больше, чем планировалось, поэтому уже за 4 дня до срока ей оставалось сшить 4 сумки. Сколько сумок в день шила швея?

4.Виды сюжетных задач. Анализ структуры сюжетных задач.

Задание. Постройте для данных ниже задач их алгебраические модели в виде систем уравнений. Для открытых задач систему уравнений сверните в вычислительную формулу:

Задача 23. Два туриста идут на встречу друг другу из городов А и В, расстояние между которыми равно 30 км. Если первый турист выйдет двумя часами раньше второго, то они встретятся через 2,6 ч после выхода второго туриста. Если же второй турист выйдет на 2 ч раньше, чем первый, то встреча произойдет через 3 ч после выхода первого туриста. Какова скорость каждого туриста?

Задача 24. Токарь должен был обработать 80 деталей к определенному сроку. Он обрабатывал в час на 2 детали больше, чем планировал, и уже за 1 ч до срока обработал на 4 детали больше. Сколько деталей в час обрабатывал токарь?

Решить задачи методом Ньютона:

1 уровень сложности.

Задача 25. Два товарища купили за 480 руб. радиоприемник, и при этом один из них отдал все свои деньги, а другой - только ¾ своих денег. Если бы первый дал ¾ своих денег, а второй – все свои деньги, то для уплаты за приемник не хватало бы 15 руб. Сколько денег было у каждого?

Задача 26. За 10 ч пароход прошел 175 км по течению реки и потом еще 45 км против течения; в другой раз также за 10 ч он прошел 200 км вниз и 30 км вверх по реке. Какова собственная скорость этого парохода?

2 уровень сложности.

Задача 27. Два пешехода выходят навстречу друг другу из двух пунктов, расстояние между которыми 30 км. Если первый выйдет на 2 ч раньше второго, то он встретит второго пешехода через 4,5 ч после своего выхода. Если второй выйдет на 2 ч раньше первого, то он встретит первого пешехода через 5 ч после своего выхода. С какой скоростью идет каждый пешеход?

Задача 28. Из двух пунктов, расстояние между которыми 36 км, отправляются навстречу друг другу велосипедист и пешеход. Если велосипедист отправится в путь на 1 ч раньше пешехода, то они встретятся через 1,5 ч после выхода пешехода. Если пешеход выйдет на 1 ч раньше велосипедиста, то они встретятся через 2 ч после выезда велосипедиста. Найдите скорости велосипедиста и пешехода.

Метод Декарта

1 уровень сложности .

Задача 29. Бригада рабочих должна была изготовить определенное количество деталей за 20 дней. Однако она изготавливала в день на 70 деталей больше, чем планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось изготовить 140 деталей. Сколько деталей должна была изготовить бригада?

Задача 30. Два трактора израсходовали 234 л горючего, причем первый расходовал в час на 0,5 л меньше, чем второй, а работал на 1,5 ч больше. Сколько горючего в час расходовал каждый трактор, если они израсходовали горючего поровну?

2 уровень сложности.

Задача 31. Гипотенуза прямоугольного треугольника равна 10 см, а один из катетов на 2 см больше другого. Найдите катеты треугольников.

Задача 32. Для сада выделен прямоугольный участок земли определенной площади. Длина изгороди, которой будет обнесен сад, окажется меньшей, если прямоугольный участок заменить квадратным той же площади. Для этого надо длину участка уменьшить на 40 м, а ширину увеличить на 30 м. Какова длина и ширина выделенного участка?

Метод одной вспомогательной задачи.

Установите для каждой из приведенных ниже задач:

• сколько неизвестных имеется в задаче;
  
• сколько данных;
  
• сколькими способами можно произвести выбор главного неизвестного и основного данного;
  
• сколько из этих выборов приводит к построению вспомогательной задачи открытого типа, решаемой цепным способом, т.е. к составлению одного уравнения с одним неизвестным.
  

Задача 33. Из А в В вышел пешеход, а через 2 часа из В в А выехал велосипедист. Двигаясь со скоростью, превышающей скорость пешехода в 3,4 раза, велосипедист прибыл в А на 1 ч 36 мин. раньше, чем пешеход прибыл в В. Зная, что расстояние АВ равно 25,5 км, найти скорость пешехода.

Задача 34. Длина средней по величине стороны треугольника равна полусумме длин большей и меньшей сторон, а удвоенная большая сторона на 3 см больше суммы двух других сторон. Определить стороны треугольника, если его периметр равен 42 см.

Задача 35. Два туриста выходят одновременно из одного города в другой. Первый проходит в час 4 км. Второй проходит в час 5 км, и по этому он приходит в другой город на 1 ч раньше первого. Каково расстояние между городами? Составьте для этой задачи всевозможные уравнения при всех различных выборах главного неизвестного и основного данного.

1 уровень сложности.

Задача 36. Ширина прямоугольника в 2 раза короче его длины. Если длину прямоугольника увеличить на 36 см, а ширину – на 48 см, то ширина составит 2/3 длины. Определить стороны прямоугольника.

Задача 37. Сумма лет трех братьев равна 45. Пять лет назад число лет старшего брата равнялось сумме лет остальных братьев, а через 7 лет лета среднего брата будут составлять ½ суммы лет остальных братьев. Сколько лет каждому из братьев?

2 уровень сложности.

Задача 38. Из пункта А в пункт В, расстояние между которыми 6 км, одновременно выходит пешеход и выезжает велосипедист. Велосипедист доезжает до пункта В, сразу же поворачивает обратно и встречает пешехода через 36 мин после выезда из А. Известно, что скорость велосипедиста на 10 км/ч больше скорости пешехода. На каком расстоянии от пункта А произошла встреча?

Задача 39. На соревнованиях по картингу по кольцевой трассе один из картов проходил круг на 5 мин медленнее другого и через час отстал от него ровно на круг. За сколько минут каждый карт проходил круг?

Метод решения задач с неопределенными неизвестными:

1 уровень сложности.

Задача 40. На первой и второй полках лежало вместе 90 книг, а на первой и третьей полках лежало вместе 75 книг. На сколько больше книг лежало на второй полке, чем на третьей?

Задача 41. Одним и тем же количеством сена можно прокормить одну корову в течение 60 дней, а одну лошадь – в течение 36 дней. На сколько дней хватит этого сена для коровы и лошади вместе при той же дневной норме?

Задача 42. Чтобы проплыть некоторое расстояние на лодке по течению реки, требуется втрое меньше времени, чем проплыть то же расстояние против течения. Во сколько раз собственная скорость лодки больше скорости течения реки?

2 уровень сложности.

Задача 43. Два косца, работая вместе, скосили некоторый участок поля за 8 ч. Если бы они работали вместе только 2 ч, а потом один из них прекратил работу, то второй, работая один, скосил бы оставшуюся часть за 10 ч. За сколько часов каждый косец в отдельности мог бы скосить весь участок?

Задача 44. Из одного селения вышел пешеход. Через 4,5 ч после выхода пешехода по тому же направлению выехал велосипедист, скорость которого в 2,5 раза больше скорости пешехода. Через сколько часов после выхода пешехода его догонит велосипедист?

5. Графическое решение сюжетных задач.

Решите графическим способом следующие задачи.

1 уровень сложности.

Задача 45. Два туриста отправляются одновременно друг другу навстречу из двух мест, находящихся на расстоянии 18 км. Через сколько времени они встретятся, если первый проходит в 1 ч 4 км, а второй – 5 км?

Задача 46. Из пункта К в пункт М вышли два туриста. Первый, выйдя часом раньше второго, пришел в пункт М часом позже его. Скорость первого туриста 4 км/ч, скорость второго 6 км/ч. Определить расстояние между пунктами К и М.

Задача 47. Сколько следует взять кипящей воды (100⁰С) и воды комнатной температуры (16⁰С), чтобы получить 100 л воды температуры в 58⁰С?

2 уровень сложности.

Задача 48. Из пункта М в пункт К вышел пешеход. Вслед за ним через 2 ч из М выехал велосипедист, а еще через 30 мин – мотоциклист. Они двигались равномерно без остановок. Через некоторое время оказалось, что все трое проделали одинаковую часть пути от М до К. На сколько минут раньше пешехода в пункт К прибыл велосипедист, если пешеход прибыл в К на 1 ч позже мотоциклиста?

Задача 49. Муравьишка был в гостях в соседнем муравейнике. Туда он шел пешком, а обратно ехал: первую половину пути он ехал на Гусенице – в 2 раза медленнее, чем шел пешком, а вторую половину пути он ехал на Кузнечике – в 5 раз быстрее, чем пешком. На какой путь Муравьишка затратил времени меньше: в гости или обратно?

Задача 50. Расстояние между двумя поселками 12 км. Ваня вышел из своего поселка в 9ч 35мин. и пришел в другой поселок в 13ч 15мин. Там он переночевал и на второй день вышел оттуда в 1ч и пришел домой в 14ч 40 мин. На каком расстоянии от своего поселка находится пункт, который Ваня проходил в один и тот же час, как на прямом пути, так и на обратном