Geum.ru

Методичні рекомендації з курсу методика викладання математики в початкових класах до самостійної роботи студентів денної форми навчання

Вид материалаМетодичні рекомендації

Содержание


Мета вивчення
Література: [2,3,4,6,7,8,9].
У концентрі "100" вивчають такі питання
Особливості вивчення усної та письмової нумерації.
Додавання і віднімання в межах сотні.
Розглянемо методику роботи над кожним названих розділів.
На першому
Подобный материал:
1   ...   6   7   8   9   10   11   12   13   ...   20







Запитання і завдання до теми:
  1. Чому перший десяток виділено в окремий концентр?
  2. З’ясувати завдання і зміст роботи в підготовчий період.
  3. Обґрунтувати необхідність використання наочних посібників та іншого дидактичного матеріалу при вивченні чисел першого десятка.
  4. Які особливості вивчення нумерації чисел першого десятка за новою програмою?
  5. Які існують прийоми додавання і віднімання в межах першого десятка і в яких випадках доцільно застосувати кожний з них? Покажіть на прикладах.
  6. З’ясуйте, яке значення має впровадження букви х для позначення невідомого при розв’язуванні простих задач і прикладів на додавання і віднімання в межах десяти?
  7. Які вправи в межах першого десятка особливо сприяють розвитку функціонального мислення учнів? Наведіть приклади вправ.

ТЕМА № 9

Тема. Методика вивчення нумерації і дій над числами першої сотні. Система розміщення даної теми у підручнику.

Мета вивчення: розширити знання студентів з методики вивчення усної та письмової нумерації цілих невід'ємних чисел і арифметичних дій над ними у концентрі сотня.

Література: [2,3,4,6,7,8,9].

Обладнання: підручники з математики 2 клас, таблиці, набірне полотно з додатком (цифри, геометричні фігури, предметні картки). Відеозапис "Від 1 до 100" (жорсткий диск).

План

  1. Причини виділення сотні в окремий концентр.
  2. Особливості вивчення усної та письмової нумерації.
  3. Додавання і віднімання в межах сотні.
  4. Множення і ділення в межах сотні: табличне множення, позатабличне множення, особливі випадки множення і ділення.

1. Причини виділення сотні в окремий концентр. Нумерацію чисел у межах 100 і чотири арифметичні дії над ними виділяють в окремий концентр з таких причин. Учні ознайомлюються з новою лічильною одиницею - десятком і з найважливішим поняттям десяткової системи числення - поняттям розряду. Засвоєння принципів утворення, називання і записування двоцифрових чисел — основа для засвоєння усної і письмової нумерації чисел за межами сотні.

Вивчаючи арифметичні дії над числами в межах 100, учні опановують основні

прийоми усних обчислень і водночас засвоюють теоретичний матеріал, який лежить в основі їх. Тут учні засвоюють напам’ять таблицю додавання і таблицю множення.

Знання цих таблиць дає можливість швидко виконувати і відповідні випадки

обернених дій віднімання та ділення.

У концентрі "100" вивчають такі питання:

а) нумерацію чисел;

б) додавання та віднімання в межах 100;

в) множення і ділення в межах 100.

У тісному зв’язку з вивченням нумерації чисел і арифметичних дій формують поняття про величини і вимірювання їх, розв'язують прості і складені задачі, розглядають числові рівності та нерівності, найпростіші рівняння з одним невідомим.

Учні ознайомлюються з буквою, як символом змінної, починають оперувати виразами. Тобто починають вивчати елементи алгебри, та геометрії.

2. Особливості вивчення усної та письмової нумерації. Завдання вчителя під час вивчення теми " Нумерація чисел у межах сотні " - навчити дітей лічити до ста, показати, як утворюються числа з десятків і одиниць, навчити читати і записувати двоцифрові числа на підставі міцного знання того, що одиниці пишуться на першому місці, а десятки - на другому, рахуючи справа наліво. Добитися, щоб учні засвоїли нові поняття і терміни: одиниці І і II розрядів, розрядне число (24=20+4), сума розрядних додатків, одноцифрове і двоцифрове число.

Під час вивчення нумерації в межах 100 виділяють два ступені: спочатку вивчають нумерацію чисел 11-20 (І ступень), а потім 21-100 (П ступень). Такий порядок вивчення зумовлюється тим, що назви чисел другого десятка утворюються з таких самих слів, що й назви розрядних чисел (12-20,13-30, 16-60). Проте слова "два", "три", "п’ять" і т.д. у числівниках дванадцять, тринадцять і т.д. позначають число одиниць, а в числівниках двадцять - дев'яносто дев’ять позначають число десятків ( за винятком 40 і 90 ). Крім того, в запису чисел другого десятка 11-19 порядок називання розрядних чисел з яких вони складаються і порядок запису не збігаються: Спочатку називають одиниці ( три-на-дцять), а пишуть першим десяток 13, тоді як у всіх інших випадках читання і записування розрядних чисел збігаються ( 21, 22... 25, 146... ). Зважаючи на ці особливості нумерацію чисел другого десятка треба розглянути окремо.

Проте нумерація двоцифрових чисел до 20 і понад 20 принципово схожа: усна і письмова нумерація цих чисел ґрунтується на десятковому групуванні одиниць під час лічби і на принципі помісного значення цифр під час записування чисел, тому нумерація чисел від 11 до 20, від 21 до 100 вивчається в одному концентрі.

Спочатку вивчають усну нумерацію чисел другого десятка, формуючи в дітей поняття про десяток. Відлічуючи по 10 паличок і зв'язуючи їх у пучок, учні дізнаються про нову лічильну одиницю "десяток". Якщо до десятка додати ще одну паличку то стане один-на-дцять тобто 11. Отже у числі 11 є 1 десяток і 1 одиниця. За такою методикою вивчаються числа 11-19

На наступному етапі вивчають письмову нумерацію.

Щоб розкрити помісний принцип записування двоцифрових чисел використовують абак.

Виконуючи вправи на записування чисел, учні закріплюють знання десяткового складу порядку слідування чисел у межах 20. Наприклад: учитель пропонує записати число з одного десятка і дев’яти одиниць, або число, яке йде за

числом 15 (16), або передує числу 15(14). Діти виконують різні вправи і пояснюють, чому вони записали так те або інше число.

Нумерацію чисел у межах від 21-100 вивчають за таким самим планом, як і в межах 11-20 спочатку вивчають усну, потім письмову нумерацію. Під час вивчення письмової нумерації учні ознайомлюються з розрядом і розрядним числом. Учитель пояснює, що у числі. 57 є 5 десятків і 7 одиниць, або інакше 5 одиниць другого розряду і 7 одиниць першого розряду. При цьому корисно використати наочний посібник – абак, або картки з розрядними числами. Практичні дії з картками допомагають дітям сформувати вміння записувати число у вигляді суми розрядних додатків, ( 48= 40+8) що потрібні для виконання дій над двоцифровими числами.

3 . Додавання і віднімання в межах сотні. Внаслідок вивчення теми, учні повинні навчитися свідомо додавати і віднімати будь-які числа в межах ста, міцно засвоїти табличні випадки додавання і віднімання з переходом через десяток, а також ряд теоретичних питань. Додавання і віднімання вивчають у такому порядку.

1. У першому класі спочатку вивчають додавання і віднімання круглих чисел. (70+20, 50+30), 2 клас с. 93-95.
  1. Потім розглядають властивості додавання числа до суми (а+в)+с = (а+с)+в або

(в + с) + а. Ці властивості вводять для випадків додавання виду;46 + 20; 46+2 (40 + 6) + 20 = (40 + 20) + 6=80 + 6 = 86. Тут же, використовуючи прийом переставлення додатків, розглядають випадок (2 + 46) або (20 + 46).
  1. Далі вивчають властивість віднімання числа від суми (а + в) - с = (а - с) + в,

де а > с, або (в-с)+а, де в > с, які ґрунтуються на цій властивості.


а. 48-30=(40+8)-30=(40-30)+8=10+8=18;

б. 48 - 3 = (40 + 8 )-3 = 40 + ( 8 - 3 ) = 40 + 5 = 45;

в. 40 – 3 = (30 + 10) - 3 = 30 + ( 10 - 3 ) = 30 + 7 = 37.

4. Потім розглядають властивість додавання суми до числа, а + ( в + с ) = (а + в) + с або (а+с)+в на підставі цієї властивості розкривають табличні випадки додавання з

переходом через десяток 7 +4; 9+3 = 9+(1+2)=(9+1)+2=12.

5. Після цього вивчають властивість віднімання суми від числа а-(в+с)-(а-в)-с або ( а - с) - в і табличні випадки віднімання ( 12 - 5 ).

6. Нарешті, розглядають парами прийоми додавання і віднімання, які ґрунтуються на двох останніх властивостях (4,5):

47+9 і 47-9; 30+12 і 30-12; 65+14 і 65-14; 36+19 і 36-19 = 36-(10+9)= (36-10)-9 = 17. У другому класі вивчають властивості додавання:

7. Суми до суми. Наприклад: (7+2)+(3+8) = (7+3) + (2+8) = 10+10=20; 53+26=(50+20) + ( 3+6 ) = 70 + 9=79.

8.Віднімання суми від суми, (а+в) - (с+d) на основі яких вводять прийоми порозрядного додавання і віднімання.

Наприклад: (7+5)-(3+4)=12-7=5

(7+5)-(3+4)=(7-4)+(5-3)=3+2=5

4. Множення і ділення в межах сотні. Однією з основних тем програми з математики для другого класу є множення і ділення в межах ста. Ця тема включає ряд питань теорії, на основі якої вивчають:
  1. табличне множення і ділення,
  2. позатабличне множення і ділення,
  3. ділення з остачею
  4. особливі випадки множення та ділення ( з одиницею і нулем ).

1. До табличного множення належать випадки множення одноцифрових

натуральних чисел на одноцифрові натуральні числа, результати яких визначають на основі змісту дії множення ( знаходять суми однакових доданків ), наприклад:

8 • 2; 6 • 3...

Випадки ділення, які відповідають цим прикладам, також називають табличними випадками ділення. Наприклад: 16 : 2, 18 : 3.(яке число треба помножити на 2, щоб дало 16? Це число 8).

2. До позатабличних випадків належать множення і ділення в межах 100 двоцифрового числа на одноцифрове, множення одноцифрового на двоцифрове, а також ділення двоцифрового числа на двоцифрове.

До особливих випадків належать множення і ділення з числом нуль, а також множення і ділення на 1, ділення з остачею. Внаслідок вивчення множення і ділення в межах 100 учні повинні засвоїти: поняття про дії множення, ділення, зв’язок між компонентами і результатами дій множення і ділення, деякі властивості дій; знати напам’ять таблицю множення і відповідні випадки ділення, засвоїти ряд обчислювальних прийомів.

Розглянемо методику роботи над кожним названих розділів.

Табличне множення. Таблиці множення та ділення вивчають у два етапи. На першому етапі формують знання про самі дії множення і ділення, на другому етапі - основну увагу приділяють засвоєнню учнями таблиць множення і відповідних випадків ділення.

На першому етапі насамперед розкривають конкретний зміст множення та ділення. Множення розглядають як знаходження суми однакових додатків. (00+00+00 по 2х3).

- Що можна сказати про доданки цієї суми? ( однакові ) Скільки їх? (3).

- Висновок: 2+2+2=6.

- Якщо доданки однакові, то суму можна записати інакше по 2х 3 рази.

Наступний другий етап дії множення - це розкриття переставної властивості

множення.

а • в = с; в • а = с. Щоб створити кращі умови для вивчення табличних випадків множення і ділення, розкривають зв’язок між компонентами і результатом дії множення, а також узагальнюють два види ділення. Наприклад: 4 • 6 = 24; 24 : 4 =6; 24 : 6 = 4.

Основою для цього є знання учнями зв’язку між компонентами і результатом дії множення.

Позатабличне множення і ділення вивчають у такому порядку.
  1. Спочатку розглядають властивості множення числа на суму 5· (6+2)=5·8=40 і суми на число (3+4) ·6=7·6=42.

Потім вивчають множення і ділення чисел, які закінчуються нулем. Наприклад: .

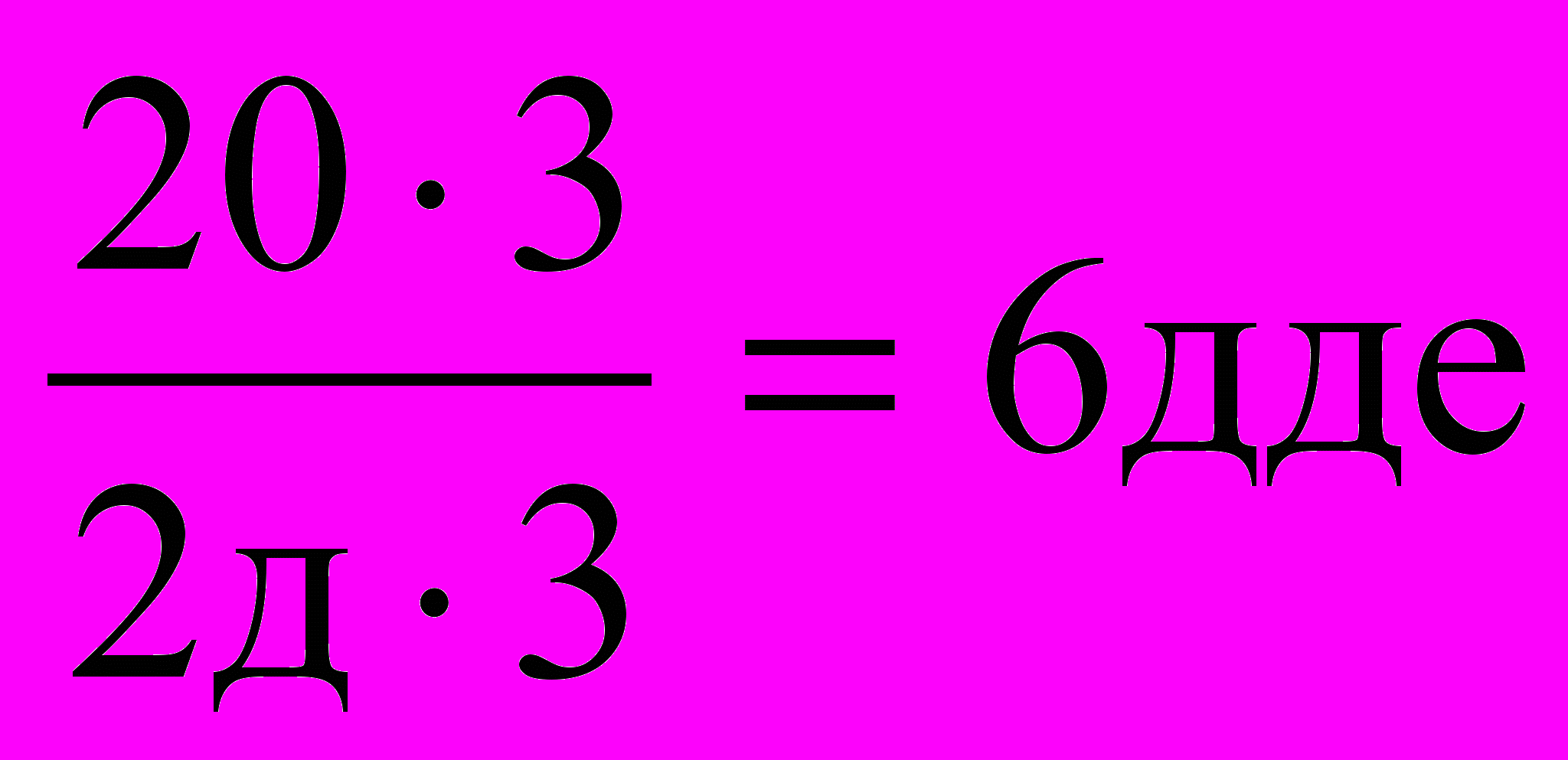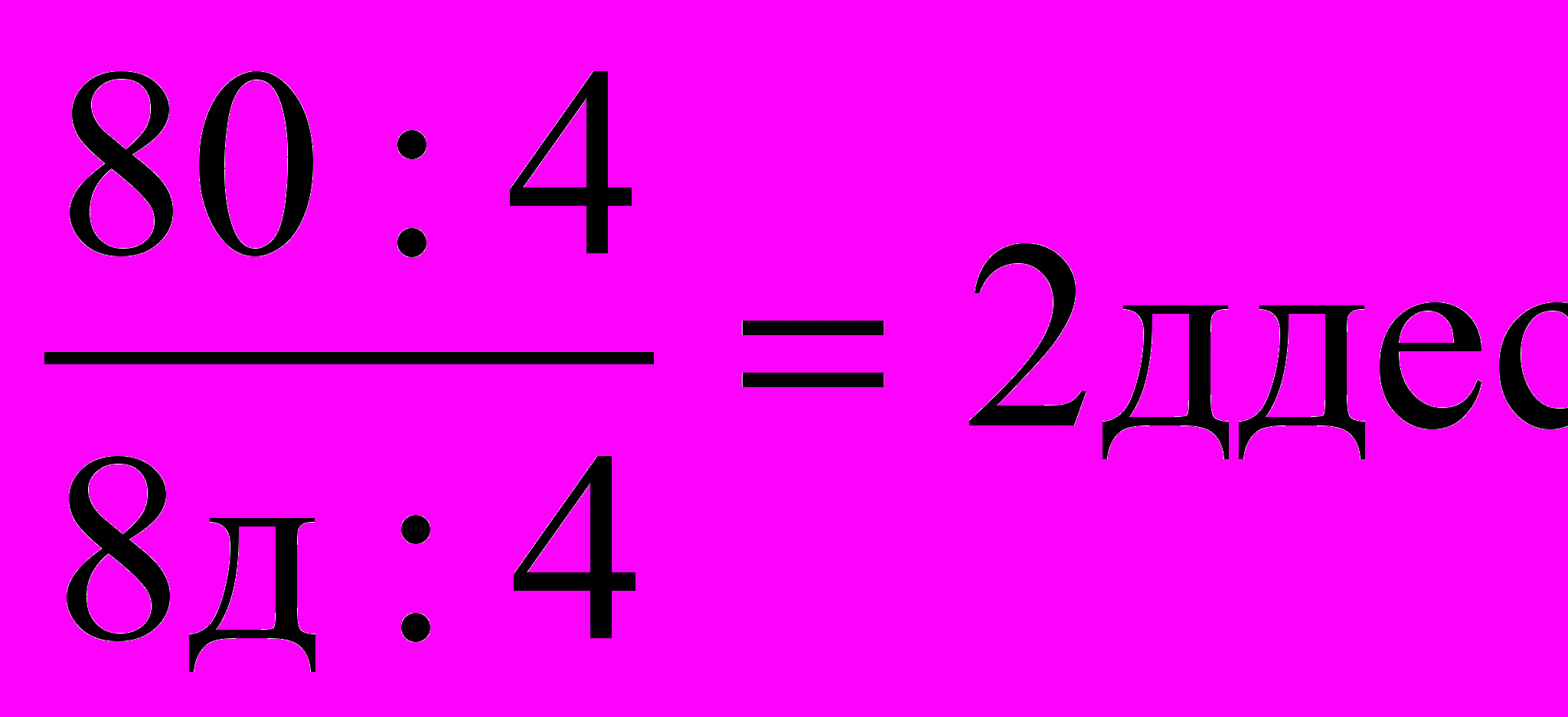
3. Далі вводять множення двоцифрового числа на одноцифрове 16·3=(10+6) ·3 =10·3+6·3 ==30+18 =48

Далі множення одноцифрового числа на двоцифрове 3•14 = 3 • (10 +4) = З0 + 12 =42

4. Далі вводять властивість ділення суми на число ( а + в ) : с на основі якої розкривають прийом ділення двоцифрового числа на одноцифрове. Наприклад: 46 : 2 = ( 40 + 6 ): 2 = 40 : 2 + 6 : 2 = 20+3 = 23; 72 : 6 = ( 60 +12): 6 = 60:6 + 12:6 =10+2=12.

І нарешті розглядають ділення двоцифрового числа на двоцифрове. Під час вивчення цієї теми вводять перевірку множення і ділення. Наприклад: 81:27 = 3. Учитель ставить запитання. На яке число треба помножити число 27, щоб дістати 81. 81 : 27 =2 мало, беремо 3, 81 : 27 = 3. Під час ділення двоцифрового числа на двоцифрове слід показати дітям деякі прийоми добору частки:

1. способом підбору проб 1, 2, 3, 4...

2.спосіб уважності вивчення чисел, наприклад: 77 : 11 = 7; 30 : 15 = 2 і т.д.

Особливі або окремі випадки множення і ділення.

Після вивчення всіх випадків табличного множення і ділення розглядають окремі випадки: множення нуля і множення на нуль, ділення нуля, множення та ділення на одиницю.

Спочатку вводять випадок множення нуля на будь-яке число ( 0 · 5, 0 · 2 ).

Результат учні знаходять додаванням 0+0+0+0+0=0 отже 0·5=0 Якщо 5 · 0 то результат не можна знайти додаванням, не можна використати і переставленням множників. Бо це нова область чисел, в якій переставна властивість множення не розкривалась. Тому друге правило: Будь-яке число помножене на нуль дорівнює нулю. Учитель просто повідомляє.

Ділення нуля на будь - яке число, яке не дорівнює 0 (0 : 6) розглядають на основі зв’язку між компонентами і результатом множення. Учні міркують так: щоб нуль поділити на шість, треба знайти число, при множенні якого на 6 буде 0. це 0, бо 0 : 6=0.

І
а : 0

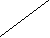, як відомо, ділити на нуль не можна.

Далі розглядають випадки множення та ділення на 1·6·1=6; 6:1=6.


Запитання і завдання до теми:
  1. З яких міркувань нумерацію чисел і чотири арифметичної дії першої сотні виділяють в окремий концентр?
  2. Які особливості вивчення усної та письмової нумерації в межах 100?
  3. В якому порядку розглядаються дії додавання і віднімання в межах 100?
  4. Методика вивчення дій множення та ділення в межах 100?
  5. Сформулюйте властивості додавання суми до числа віднімання суми від числа та на конкретних числових прикладах поясніть прийоми додавання і віднімання основані на цих властивостях.

30+18= 40-16=

37+12= 56-35=

18+6= 13-6=

46+8= 45-7=

29+36= 43-25=

6. Розкрийте конкретний зміст дій множення і ділення та на конкретних прикладах складіть таблицю множення і ділення числа 2.

……+…..+……+…..+..= .... …. х 4 = ......

7.Скласти таблиці множення на 3…9 і обернену до них таблиці ділення.

8. Наведіть різні види завдань, які підготовляють учнів до ознайомлення з діями множення і ділення. Як учні записують розв’язання таких завдань?

9.Розглянути публікації з журналів та газети “Початкова школа”, “Начальная школа”, “Розкажи онуку”, “Освіта” (висвітлення актуальних проблем заданої теми). Форма роботи – обговорення повідомлень.

Тема № 10

Тема. Методика вивчення нумерації і дій над числа

ми у межах тисячі.

Мета вивчення: навчити студентів методики вивчення нумерації цілих невід'ємних чисел і арифметичних дій над ними у концентрі тисяча

Література: І.З.Василенко. Методика викладання математики в початкових класах. - К., Вища шк. 1971р.

Богданович М.В. Методика вивчення нумерації чисел і арифметичних дій в початковій школі. - К., 1990.

Моро М.Г., Пишкало А.М. Методика навчання математики в 1 - 3кл.- К.,1979.

Друзь Б.Г. Творчі вправи з математики для початкових класів.