Методичні рекомендації з курсу методика викладання математики в початкових класах до самостійної роботи студентів денної форми навчання
| Вид материала | Методичні рекомендації |
- Методичні рекомендації та завдання для самостійної роботи студентів денної та заочної, 2076.33kb.
- Програма, плани семінарських занять та методичні рекомендації щодо самостійної роботи, 372.3kb.
- Методичні рекомендації з організації самостійної роботи студентів денної форми навчання, 287.4kb.
- Методичні рекомендації до самостійної роботи студентів для усіх напрямків підготовки, 576.6kb.
- Тематичний план аудиторної та самостійної роботи 7 Перелік тем та питань самостійної, 209.58kb.
- Містить рекомендації по організації самостійної роботи, зокрема, по підготовці студентів, 499.21kb.
- Програма курсу І методичні вказівки до самостійної роботи студентів заочної форми навчання, 665.46kb.
- Методичні вказівки до виконання практичних занять І самостійної роботи з дисципліни, 583.93kb.
- Навчально методичний посібник для організації самостійної роботи студентів з курсу, 1628.28kb.
- Методичні рекомендації для самостійної роботи Для студентів денної І заочної форми, 516.83kb.
План
1. Урок, як основна форма організації навчання. Види уроків та їх структура.
2. Умови ефективності уроку.
3. Підготовка вчителя до уроку. Планування.
4. Позакласна та позаурочна робота з математики.
1. В початкових класах навчають математики у школі у формі уроків і позаурочних занять (індивідуальних і групових); вдома або в групі продовженого дня - у формі домашньої, самостійної роботи; у природі, музеї, на виробництві - у формі екскурсії.
Урок — це основна форма організації навчальної діяльності учнів. Класно-урочну систему навчання було створено під впливом тих вимог, які ставило суспільство до школи й освіти наприкінці 16 століття.
Великий чеський педагог Ян Амос Коменський вперше обґрунтував організаційні форми класно-урочної системи навчання дітей. Він сформулював об'єктивно необхідні дидактичні вимоги, додержання яких давало можливість учителеві добитися в навчанні дітей кращих результатів і в значно коротші строки, ніж це було в школах середньовіччя.
Дидактичні принципи навчання, сформульовані Я.А. Каменським, лягли в основу методики викладання основ наук, зокрема і математики. З часом методи викладання її вдосконалювались завдяки розвитку медицини, фізіології, психології.
Палким прихильником класно-урочної системи навчання був видатний вітчизняний педагог К.Д. Ушинський. який обґрунтував загально-дидактичні і психологічні форми уроку. Особливо цінним є його вчення про типи і структуру уроку, про підготовку вчителя до занять, про педагогічний такт, чим здебільшого зумовлюється і дисципліна учнів.
Класична педагогіка, залежно від основної дидактичної мети навчальної роботи, якій підпорядковуються усі інші завдання уроку встановила такі типи уроків:
1. Урок вивчення нового матеріалу.
2. Урок закріплення знань, умінь, навичок.
3. Урок повторення і систематизації знань учнів.
4. Урок контролю або обліку знань, умінь, навичок.
5.Комбінований урок, якщо урок має не одну дидактичну мету, а кілька.
Структура уроків (5 типів).
1. Урок вивчення нового матеріалу
У молодших класах спеціальних уроків математики, цілком присвячених вивченню нового матеріалу, немає. Новий матеріал невеликими частинами розглядають майже на кожному уроці. Проте бувають уроки, на яких вивчення нового матеріалу є основною дидактичною метою. Цій роботі відводять більшу частину уроку, при цьому інші частини уроку також підпорядковані вивченню нового. Структура згаданого типу уроку може бути така:
1. Перевірка домашнього завдання;
2. Повторення матеріалу потрібного для свідомого засвоєння нових математичних знань;
3. Вивчення нового матеріалу;
4. Попереднє закріплення нового матеріалу;
5. Завдання до дому;
Послідовність структури елементів може бути і іншою, але основна частина уроку присвячена вивченню нового матеріалу.
2. Урок закріплення знань, умінь, навичок.
Основне місце на уроках цього типу займає виконання учнями різних тренувальних вправ і творчих робіт. Пропонують вправи за певною системою. Структура таких уроків як правило така.
1. Перевірка домашнього завдання;
2. Відтворення учнями знань, умінь і навичок, які потрібні для виконання завдань;
3. Самостійне виконання учнями різних вправ;
4. Перевірка виконання роботи.
5. Підведення підсумків;
6. Завдання додому.
З метою розвитку знань, умінь і навичок на таких уроках іноді включаються елементи нового. Крім того, попутно або за допомогою спеціальних вправ здійснюють підготовчу роботу до вивчення наступних тем.
3. Урок повторення і систематизації знань учнів.
Структура цього уроку схожа на структуру уроку закріплення знань. На початку навчального року, або чверті проводять уроки повторення вивченого, щоб повторити і систематизувати ті знання, які потрібні для вивчення нових тем. Наприкінці вивчення теми, або розділу на уроках повторення використовують вправи узагальнюючого і систематизуючого характеру.
4. Урок контролю, або обліку знань.
Основне місце на таких уроках відводять усній і письмовій перевірці засвоєння вивченого матеріалу. Як правило, перевірку поєднують із закріпленням знань, умінь і навичок. Самостійні письмові роботи тривають від 15 до 30 хвилин (із 45 хв.), решту часу відводять на закріплення раніше вивченого. Наприкінці уроку, якщо перевірку здійснювали в усній формі, учитель, як правило, дає коротку характеристику знанням, умінням і навичкам учнів, вказує на досягнення і недоліки, і шляхи усунення їх.
Якщо перевірку здійснювали у письмовій формі, то наступний урок присвячується аналізу результатів контрольної роботи, виправленню типових помилок, повторенню і закріпленню тих розділів, які були гірше засвоєні.
5. Комбіновані уроки найбільш поширені в 1 - 4 класах, що пояснюються віковими особливостями молодших школярів, а також особливостями побудови початкового курсу математики.
Структура уроків комбінованого типу може бути різною:
Розглянемо структуру сучасного комбінованого уроку. Він включає такі компоненти:
1) перевірка домашнього завдання;
2) опитування учнів вивченого на попередньому уроці;
3) усні обчислення;
4) підготовка до вивчення нового матеріалу і повідомлення теми уроку;
5) опрацювання нового матеріалу;
6) первинне закріплення;
7) закріплення і повторення;
8) домашнє завдання;
9) підсумок уроку.
У структурі комбінованого уроку його компоненти можна об’єднати в такі три частини:
1. Частина. Контроль, корекція та закріплення знань учнів (сюди входить 1,2,3 пункти).
П. частина. Опрацювання нового матеріалу (сюди входить 4,5,6 пункти);
Ш. Частина. Закріплення та узагальнення знань учнів (сюди входить 7,8,9 пункти).
На уроці комбінованого типу витрачають приблизно однаковий час на всі етапи уроку.
2. Кожен урок математики має свою тему і мету. Ефективність уроку саме й визначається мірою досягнення його навчально-виховної мети. Зупинимося на деяких загальних і організаційних вимогах до проведення уроку .
- Кожний урок математики повинен забезпечувати зв’язок навчання математики з життям з іншими предметами, де це можливо.
- Учні повинні бути обізнані з темою уроку, його метою . У кінці уроку пови нен бути підсумок уроку.
- Учні 1—4 класів можуть продуктивно займатися одним якимось видом навчальної діяльності 10 - 15 хвилин, тому вчитель повинен застосовувати різні види навчальної роботи на уроці і забезпечувати плавний перехід від одного до наступного виду.
- Новий матеріал учні повинні усвідомити і засвоїти на уроці, а його повторення і закріплення може бути пов'язано з пройденим раніше матеріалом.
- У процесі навчальної роботи вчителеві треба виявити які є труднощі в окремих учнів, це дає можливість вчасно допомагати учням.
- Велике значення має темп, в якому вчитель веде урок. Надто швидкий темп навчальної роботи перешкоджає слабшим учням. Проте і надто повільний темп не стимулює учнів працювати вправно.
- Вчителеві постійно треба дбати про раціональне використання навчального часу, про вдосконалення самої техніки проведення уроку. Наочне приладдя та дидактичні матеріали треба готувати заздалегідь і зручно розміщувати його. Вправи для с.р. треба записувати до уроку. У кінці уроку слід виставити оцінки у журнал, прокоментувавши кожну оцінку. Розглянемо від чого ще можна залежати ефективність уроку.
3. Успішне вивчення математики великою мірою залежить від правильного планування матеріалу навчальної програми.
Виходячи з програми, учитель складає так званий календарний план роботи на кожну чверть, або на півріччя.
Здебільшого тепер такі плани (друкуються у журналах ПШ, або у навчальних методичних посібниках), вчитель тільки вносить в них відповідні уточнення, або поправки, виходячи з конкретних умов даного класу.
Тематичне планування полягає в тому, що вчитель відповідно до кількості навчальних годин, орієнтовано визначених програмою на вивчення певної теми, і матеріалу підручника визначає мету кожного уроку. При цьому він зазначає, яке обладнання використає на уроці, які вправи, задачі розв'яже на уроці, а які задасть додому.
Як бачимо, при тематичному плануванні вчитель не визначає ні порядку розв'язання завдань, ні форми організації навчальної діяльності учнів
Виходячи з загальних вимог до уроку, його мети і вимог до методів навчання, вчитель складає поурочний план, в якому треба зазначити:
- Тему уроку і його мету.
- Обладнання, яке треба підготувати і використати на уроці.
- Який матеріал треба повторити з учнями, щоб на його основі вони оволоділи новим матеріалом. Вказати номери вправ чи задач з підручника чи д/ матеріалу. Доцільно записати розв'язок задач, прикладів і т. д.
- Види робіт, їх послідовність, орієнтовано вказати час, необхідний для виконання кожного виду роботи, намітити методи і форми ведення уроку.
- Вказати прізвища учнів для опитування.
- Завдання додому на дошці і зробити короткий підсумок уроку.
Молодим учителям корисно складати докладні конспекти уроків. (Зразок такого конспекту див. додаток 1.).
Вміння готуватися до уроку, складати план, або конспект уроку набувається досвідом, самокритичною оцінкою власної роботи, аналізом причин вдалих і невдалих моментів уроку. Велику користь у набуванні методичної майстерності дає спостереження і аналіз уроків досвідчених учителів.
Аналізувати урок математики можна за такою орієнтованою схемою.
4. Позакласна робота з математики сприяє зміцненню і поглибленню знань, якими оволодівають учні на уроках.
Вона стимулює їх самостійну творчу роботу, розвиває мислення й мову, підвищує успішність учнів, виховує в них інтерес і любов до математики, волю, наполегливість.
З учнями 1-2 класів учителі в позакласні години здебільшого організовують математичні ігри, розв’язують цікаві задачі, виготовляють дидактичний матеріал для своїх уроків та для дошкільників. Часто вчитель спочатку і сам бере участь у грі, а потім, коли учні зрозуміли її суть, виходить з неї. Дуже корисно в процесі добре засвоєної гри дозволити учням змінювати її, якщо це робить гру цікавішою. Організуючи позакласну роботу, вчитель повинен стежити за навантаженням дітей, не допускати перевантаження їх.
До позакласних занять відносяться:
- Масові позакласні заходи.
- Математичні гуртки.
- Математичні кутки.
- Математичні газети.
- Математичні екскурсії.
- Індивідуальна робота.
До масових позакласних заходів належать: математичні ранки (вечори), олімпіади, конкурси на кращого математика. Їх зміст: коротенькі бесіди, ігри, розв’язування задач, головоломок.
Математичні гуртки працюють за складеним і обговореним на перших організаційних зборах календарним планом. Один-два рази на місяць протягом 40 –45 хвилин. Приступаючи до організації гуртка вчитель з’ясовує, що це добровільна справа, розповідає дітям про обв’язки і завдання гуртківців.
Наприклад: (тематика роботи гуртка у журналі ПШ, стор. 349. Василенко . Методика викладання математики).
Математичний куток – доцільно організовувати у кожному класі. У 1 виготовляють наочні посібники класного і індивідуального користування, у 3 класі слід обладнати інструменти для виготовлення наочних посібників (зберігати вимірювальні прилади).
Математична газета – є хорошим засобом залученням як окремих учнів (художників, витівників) до участі в творчій роботі, так і всього учнівського колективу до розширення і збагачення математичних знань. У газеті вміщують короткі статті з історії математики, задачі, математичні ребуси, загадки. Газету створює актив класу, групи, гуртка – їм допомагають учні класу, а вчитель допомагає тільки порадами, критичною оцінкою їх роботи, в доборі матеріалу.
Математичні екскурсії повинні мати свою чітку мету. Залежно від мети вчитель вибирає найдоцільніші форми і методи керівництва пізнавальною діяльністю учнів, як під час самої екскурсії, так і в наступній роботі, що пов'язана з екскурсією і випливає з неї. Готуючись до екскурсії вчитель складає план роботи і готує дітей. Діти повинні знати що і для чого будуть робити на екскурсії (стор.352 Василенко на практичній роботі).
Індивідуальна робота. Суть індивідуального підходу полягає в тому, щоб, знаючи учня, створити такі умови, які допомогли б йому стати активним членом учнівського колективу. Вчитель повинен дбати, щоб усі його учні вчилися не нижче своїх можливостей. Середні учні є для вчителя показником ходу процесу навчальної роботи, і завдання вчителя - підтягати їх до рівня сильніших. Учнів з низькою успішністю вчитель активізує посильними їм завданнями і допомагає підвищити успішність, а сильним учням треба давати додаткові завдання підвищеної трудності, які сприяють дальшому розвитку їх здібностей.
Запитання і завдання до теми:
1. Які типи уроку, залежно від основної дидактичної мети навчальної роботи, встановила класична педагогіка? Розкрийте їх структуру.
2. Назвіть тип та структуру найбільш поширеного уроку у І-ІУ класах.
3. Розповісти про форми масової позакласної роботи.
4. Висвітлити роль і завдання учнівських математичних гуртків та зміст їх роботи.
5. Організація занять з учнями, які виявляють підвищений інтерес до математики.
- Розробити план - конспект проведення математичного ранку на будь яку тему в одному з початкових класів.
- Розробити тематику бесід для учнів - гуртківців з історії математики ( 3, 4 класів).
- Скласти план-конспект комбінованого уроку та роботи вчителя з класом (за вибором Богданович М.В. Математика 4 к. з теми Додавання багатоцифрових чисел).
- Розглянути публікації з журналів та газети “Початкова школа”, “Начальная школа”, “Розкажи онуку”, “Освіта” (висвітлення актуальних проблем заданої теми). Форма роботи – обговорення повідомлень.
ТЕМА № 5
Тема. Методика роботи над простими текстовими задачами у початковому курсі математики.
Мета вивчення: закріпити навички студентів володіти методикою роботи над простими задачами; виконувати скорочений запис задачі, відповідно до сучасних вимог; вміти аналізувати та шукати розв'язок задачі; розвивати творчість, уміння працювати з методичною літературою.
Література: [2,3,5,6,11,12,17].
Основні поняття: проста задача, схема-модель; структура задачі.
Обладнання: підручники математики (М.В. Богданович, Г.М. Захарова,
Т.І. Фещенко), зошити з друкованою основою, зразки планів-конспектів уроків з математики, зразки наочності до уроку з математики, слайди, відеозапис комбінованого уроку з математики, класифікаційні таблиці простих задач.
План.
1. Поняття "арифметична задача". Структура задачі.
2. Загальні питання методики навчання розв'язування задач.
3. Прості задачі. Їх класифікація та методика розв'язування.
4.Система розміщення простих здач у підручниках з математики 1-4 кл.
1. У навколишньому житті виникає безліч таких життєвих ситуацій, які пов'язані з числами і потребують виконання арифметичних дій над ними. Це задачі.
Арифметичною задачею – називається - вимога визначити числове значення шуканих величин, коли дано числові значення інших величин і вказана залежність, яка пов’язує ці величин які між собою, так і з шуканими величинами.
Арифметична задача складається:
а) з умови з числовими даними;
б) запитання.
В умові задачі зазначають зв'язки між числами, а також даними і шуканими, ці зв'язки і визначають вибір відповідних арифметичних дій.
Запитання визначає, яке число є шуканим.
Розв'язати задачу - означає розкрити зв'язки між даними і шуканими, задані умовою задачі, на основі чого вибрати, а потім виконати арифметичні дії і дати відповіді на запитання задачі.
Усі арифметичні задачі за кількістю дій, які треба виконати, щоб їх розв'язати, поділяються на прості і складені. Задачу, для розв'язування якої треба виконати одну арифметичну дію, називають простою.
Задачу, для розв'язування якої треба виконати кілька пов'язаних між собою дій, називають складеною.
2. Щоб навчити дітей розв'язувати задачі, вчитель повинен передбачати в методиці навчання розв'язування задач одного виду різні ступені, які мають свою мету.
Розглянемо ці ступені (три ступені).
На першому ступені вчитель готує дітей до розв'язання задачі розглядуваного виду. Учні повинні засвоїти зв'язки між величинами, на основі яких вибиратимуть дії в процесі розв'язування задач.
Виконуються різні практичні вправи з використанням дидактичного матеріалу в ігровій формі.
Наприклад, щоб навчити дітей розв'язувати задачу на знаходження суми, дітям пропонують вправи на об 'єднання множин.
Провівши відповідну підготовчу роботу, можна перейти до ознайомлення дітей з розв'язуванням задач розглядуваного виду. (до П ступеня)
На другому ступені, вчитель ознайомлює дітей з розв'язуванням задачі. На цьому ступені доцільно дотримуватись таких етапів у методиці роботи над задачею: (ст. 157 Бантова)
І етап - ознайомлення зі змістом задачі. (Записують скорочений запис).
II етап - шукання розв'язку задачі. (Учні повинні назвати величини, які входять до задачі, дані і шукані числа, встановити зв'язки між даними та шуканим і на цій основі застосувати відповідні арифметичні дії.) Для того, щоб учні могли встановити зв'язки між даними та шуканим і вибрати відповідні арифметичні дії, треба проілюструвати задачу або зробити її розбір (аналіз). Ілюстрування може бути предметне або схематичне. Предметне ілюстрування це коли використовують предмети або малюнки предметів, про які йдеться в задачі.
Схематичне ілюстрування - це короткий запис задачі де фіксуються величини, дані і шукані числа. Цей запис може бути і у вигляді таблиці, а також у формі креслення (графічного моделювання).
III етап - розв'язування задачі.
Розв'язування задачі - це виконання арифметичних дій, визначених під час складання плану розв'язування.
IV етап - перевірка розв'язку задачі.
У початкових класах використовують 4 способи перевірки:
1) Складання і розв'язання оберненої задачі.
2) Розв'язування задач різними способами.
Наприклад: І спосіб (18 + 12): 6 =5;
II спосіб 18: 6+12:6=5.
3
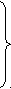
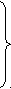) Установити відповідності між числами знайденими внаслідок розв'язування задачі і заданими числами.Наприклад: 1 - 54 кг. І — 54 кг.
2-? на 15кг. більше 180 кг. II – 69 кг. 180кг.
3-? ІП - 5І кг.
4). Прикидка
На третьому ступені, вчитель закріплює вміння розв'язувати задачі. Виробленню уміння розв'язувати задачі розглядуваного виду допомагають так звані вправи творчого характеру, а також вправи на складання і перетворення задач.
Вправи творчого характеру:
1. Розв'язування задач підвищеної трудності;
2. Розв'язування задач кількома способами.
3. Розв'язування задач із зайвими даними, або даними, яких не вистачає;
4. Розв'язування задач, що мають кілька розв'язків.
Вправи на складання і перетворення задач:
Розглянемо деякі види вправ на складання і перетворення задач:
—Постановка запитання до заданої умови задачі, або зміна цього питання:
Наприклад: в 1 коробці 48 олівців, у другій 12 олівців. Можна поставити такі запитання
1. Скільки олівців у двох коробках разом?
2. На скільки олівців у 1 коробці більше ніж у 2?
3. На скільки олівців у 2 коробці менше ніж у 1 ?
4. Скільки олівців треба перекласти у 2 коробку щоб їх стало порівну в 2-х коробках?
—2. Складання умови задачі за даними запитаннями. Наприклад: Скільки відер води в обох бочках?
—3. Добір числових даних, або зміна їх.
Наприклад: дається умова, а дані пропущені вставити, дібрати їх самому, або змінити.
—4. Складання задачі за аналогічною.
—5. Складання обернених задач.
Наприклад: у двох коробках 60 олівців, у 2 — 12 олівців. Скільки олівців у 1 коробці?
—6. Складання задач за ілюстраціями, або графічними моделями, схемами.
8 пакетів —1 пакет з печивом
(?)
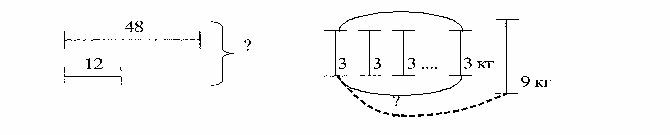
Скільки всього кілограмів солодощів
привезли у дитячий садок ?
—7. Складання задач за даним розв'язком.
Наприклад: 3 х 8 + 9 =33 (кг)
—8. Перетворення заданих задач у задачі споріднених їм видів.
3. Прості задачі, їх класифікація та навчання розв'язування простих задач.
Уміння розв'язувати прості задачі є підготовчим ступенем опанування учнями умінь розв'язувати складені задачі, бо розв'язування складеної задачі зводиться до розв'язування ряду простих задач.
Розв'язуючи прості задачі, учні вперше ознайомлюються з задачею і її складовими частинами, і опановують основні прийоми роботи над задачею.
Прості задачі можна поділити на групи відповідно до арифметичних дій, за допомогою яких їх розв'язують. Однак з погляду методики зручніша інша класифікація: поділ задач на групи залежно від тих понять, які формуються під час їх розв'язування (див. додаток 3).
До І групи належать задачі під час розв'язання яких діти засвоюють конкретний зміст кожної арифметичної дії, або яка арифметична дія пов'язана з тією або іншою операцією над множинами. У цій групі 5 видів задач:
1) Знаходження суми двох чисел.
Наприклад: Дівчинка помила 3 глибоких тарілки і 2 мілких. Скільки всього тарілок помила дівчинка?
3+2=5
2) Знаходження остачі.
Наприклад: Діти виготовили 6 шпаківень, 2 шпаківні повісили на дерево. Скільки шпаківень їм залишилось повісити?
6-2-4 (ш)
3) Знаходження суми однакових доданків.
Наприклад: У 3-х клітках жили кролі, по 2 кролі в кожній. Скільки всього кролів у живому куточку?
2-3=6(кр.)
2+2+2=6(кр.)
4) Поділ на рівні частини.
Наприклад: У двох вазах 8 яблук у кожній порівну. Скільки яблук у кожній вазі?
8:2=4 (яб.)
5) Ділення на вміщення.
Наприклад: Бригади школярів обкопали 24 дерева по 8 дерев кожна. Скільки бригад школярів виконували цю роботу?
24:8=3(б.)
До другої групи належать прості задачі, під час розв'язування яких учні засвоюють зв'язок між компонентами і результатами арифметичних дій.
До них належать задачі на знаходження невідомих компонентів.
У цій групі 8 видів.
- Знаходження першого доданка, коли відомо другий і сума.
х+5=12; х=12-5; х=7.
- Знаходження другого доданка.
7+х=12; х=5.
3) Знаходження зменшуваного, коли відомо від'ємник і остача
(різниця).
х-3=8; х=8+3; х=11.
- Знаходження від’ємника.
11-х=8;х=11-8;х=3.
- Знаходження першого множника.
х·3=21; х=21: 3; х=7.
6) Знаходження другого множника.
7-х=21; х=3.
7) Знаходження діленого.
х:3=15;х=5.
8) Знаходження дільника.
15:х=5; х=3.
До третьої групи належать задачі під час розв'язування яких розкривають новий зміст арифметичних дій.
До них належать прості задачі, пов'язані з поняттям різниці.
Цих задач 6 видів.
1). Різницеве порівняння чисел, або знаходження різниці двох чисел. (І вид)
Наприклад: Один будинок збудували за 10 тижнів, а другий за 8. На скільки більше тижнів затратили на будівництво першого будинку?
І
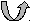-10т.П-8т на? 10-8-2(т)
2). II вид.
І-10 т.
П-8 т. на? На скільки менше тижнів затратили на будівництво другого будинку?
3). Збільшення числа на кілька одиниць (пряма форма).
Наприклад:
І
буд. - 8т.II буд. - ?, на 2 т. більше, ніж
4). Збільшення числа на кілька одиниць (непряма форма).
Наприклад: І будинок будували 8 т., це на 2 тижні менше ніж II будинок. Скільки тижнів витратили на будівництво II будинку?
І
б - 8 т., це на 2 тиж. більше, ніжII б. - ?
8+2=10(т).
5). Зменшення числа на кілька одиниць (пряма форма), (м. 3(2) стор. 68
№394).
Наприклад: 3 І куща смородини зібрали 9 кг ягід, а з другого на 2 кг. менше. Скільки кілограмів ягід зібрали з П куща?
І к. - 9 кг.
II к. - ?, на 2 кг менше
9-27=7(кущ).
6) Зменшення числа на кілька одиниць (непряма форма).
Наприклад: 3 І куща смородини зібрали 9 кг., це на 2 кг. більше, ніж з II куща. Скільки ягід зібрали з II куща?
І
к. - 9 кг.. це на 2 кг. більше, ніж з П к.-?
9-2=7(кг),
До цієї групи належать задачі пов'язані з поняттям кратного відношення.
Цих задач 6 видів.
1)Кратне порівняння чисел, або знаходження кратного відношення
двох чисел (1 вид).
Наприклад: В поле вийшло працювати 24 сівалки і 8 тракторів. У скільки разів більше вийшло сівалок ніж тракторів?
24 : 8 = 3 (рази)
2) Кратне порівняння чисел, або знаходження кратного відношення двох чисел (І вид).
Наприклад: В поле вийшло працювати 24 сівалки і 8 тракторів. У скільки разів менше вийшло в поле тракторів, ніж сівалок?
24 : 8 = 3 (рази)
3) Збільшення числа в кілька разів (пряма форма), (м 3(2) стор. 68 № 394)
Наприклад: У гаражі було 4 легкових автомобіля, а вантажних у 3 рази більше. Скільки було у гаражі вантажних автомобілів?
Л. - 4м.
В.-?, у 3р. більше, ніж легкових
4 . 3 = 12(м) – вантажних.
4) Збільшення числа у кілька разів (непряма форма).
Наприклад:
Л. – 4М., це у 3 рази менше, ніж
Г. - ?
4 . 3 = 12(м) – вантажних
5) Зменшування числа у кілька разів (пряма форма).
Наприклад: У парку росло 12 ялинок, а беріз у 2 рази менше. Скільки росло беріз у парку?
Ял. – 12
Б. - ?, у 2 рази менше, ніж ялинок
12:2= 6(б).
- Зменшення числа у кілька разів (непряма форма).
Наприклад: У парку росло 12 ялинок, це у 2 рази більше, ніж беріз. Скільки беріз у парку?
Ял. – 12, це у 2 рази більше ніж беріз
Б. - ?
12:2 = 6(б).
Тут названо лише основні види простих задач (25 видів). Однак вони не вичерпують всієї різноманітності задач. Порядок введення простих задач підлягає змісту програмового матеріалу. В 1 класі вивчають дії додавання і віднімання і в зв’язку з цим розглядають прості задачі на додавання і віднімання. У 2 класі вивчають дії ділення і множення і вводять прості задачі, які розв’язуються за допомогою цих дій.
Запитання і завдання до теми:
- Що розуміємо під арифметичною задачею?
- Які задачі називаються простими?
- Які вимоги повинен задовольняти зміст арифметичної задачі?
- Яке значення має самостійне складання і розв’язування задач учнями?
- Дібрати з підручників математика 1-4 класи по одній простій задачі, які відносяться до Ш групи. Розв’язати ці задачі, виконати запис задач відповідно до сучасних вимог.
- Пояснити методику розв’язання задач з поняттям кратного відношення.
- Пояснити методику роботи над задачами ділення на рівні частини та ділення на вміщення (Дібрати з підручника та розв’язати ці задачі).
- Скласти самостійно по одній простій задачі, що розкривають конкретний зміст кожної арифметичної дії. Розв’язати їх оформити запис розв’язання відповідно до сучасних вимог.
- Розглянути публікації з журналів та газети “Початкова школа”, “Начальная школа”, “Розкажи онуку”, “Освіта” (висвітлення актуальних проблем заданої теми). Форма роботи – обговорення повідомлень.