Методичні рекомендації з курсу методика викладання математики в початкових класах до самостійної роботи студентів денної форми навчання

Вид материала

Методичні рекомендації

Содержание Методи навчання математики в початкових класах. Література: [1,2,3,16,17,20]. Задача № 1 Задача № 1 Запитання і завдання до теми Література: [3,7,13,15,18,19].

Подобный материал:

• Методичні рекомендації та завдання для самостійної роботи студентів денної та заочної, 2076.33kb.
• Програма, плани семінарських занять та методичні рекомендації щодо самостійної роботи, 372.3kb.
• Методичні рекомендації з організації самостійної роботи студентів денної форми навчання, 287.4kb.
• Методичні рекомендації до самостійної роботи студентів для усіх напрямків підготовки, 576.6kb.
• Тематичний план аудиторної та самостійної роботи 7 Перелік тем та питань самостійної, 209.58kb.
• Містить рекомендації по організації самостійної роботи, зокрема, по підготовці студентів, 499.21kb.
• Програма курсу І методичні вказівки до самостійної роботи студентів заочної форми навчання, 665.46kb.
• Методичні вказівки до виконання практичних занять І самостійної роботи з дисципліни, 583.93kb.
• Навчально методичний посібник для організації самостійної роботи студентів з курсу, 1628.28kb.
• Методичні рекомендації для самостійної роботи Для студентів денної І заочної форми, 516.83kb.

Тема №2.

Методи навчання математики в початкових класах.

Мета вивчення: познайомити студентів з особливостями використання різних методів та логічних прийомів при навчанні математики у початкових класах. Навчити застосовувати їх на практиці.

Література: [1,2,3,16,17,20].

Обладнання: комплект підручників з математики 1-4 класи. Програми середньої загальноосвітньої школи 1-4 класи. Посібники для вчителів.

План

1. Загальні вимоги до методів навчання математики.

2. Індукція і дедукція. Аналогія. Аналіз і синтез.

3. Метод усного викладу. Пояснення вчителя. Бесіда.

4. Метод вправ, письмових і графічних робіт.

5. Самостійна робота учнів.

6. Метод лабораторних робіт при вивченні геометричного матеріалу).

7. Метод програмового навчання.

8. Проблемний метод навчання.


1. Загальні вимоги до методів навчання математики.

Методи навчання - це способи організації вчителем пізнавальної діяльності учнів. Вони забезпечують систематичність і послідовність у викладанні і засвоєнні матеріалу на уроці.

Педагогічний процес за своїм змістом і цілеспрямованістю дуже різноманітний і багатогранний. Не можна звести навчально-виховну роботу до одного якогось універсального методу, однаково придатного для виконання всіх завдань навчання і виховання учнів. Добираючи методи навчання учнів початкових класів, слід враховувати вікові особливості дітей, У них ще не розвинені увага, мислення, їм, недоступні складні спостереження. Отже, методи навчання повинні передбачати:

а) широке застосування наочності; б) забезпечувати активність у роботі всіх учнів; в) забезпечувати систематичність і послідовність у викладанні і засвоєнні матеріалу; г) оволодіння необхідними вміннями і навичками, зазначеними в навчальних програмах; д) виховання в учнів навичок самостійної роботи; є) зв’язок навчання з життям, з працею учнів; є) вироблення в дітей почуття колективізму і навичок колективної праці; ж) виховання в учнів почуття відповідаль­ності за виконання своїх обов’язків; з) розвиток естетичного почуття дітей, їх емоцій, уваги, волі, пам’яті, мисленню; і) сприяти нормальному фізичному розвитку дітей.

Викладання кожного предмета потребує застосування своїх методів, зумовлених змістом і специфікою – навчального матеріалу. Процес навчання математики визначається здебільшого такими основними етапами навчальної роботи:

1. Пояснення вчителем нового матеріалу.

2. Сприймання і засвоєння учнями знань.

3. Закріплення одержаних знань.

4. Перевірка і оцінювання знань, умінь і навичок учнів.

Ці етапи перебувають у взаємозв'язку і підпорядковуються меті уроку.

1. Ефективність першого етапу залежить від ставлення вчителя до роботи, його кваліфікації, досвіду, любові до дітей, індивідуального підходу до них в умовах роботи з класом.
   
2. У тісному зв’язку з першим етапом перебуває другий етап. Суть сприймання нового матеріалу учнями полягав в утворенні у дітей нових уявлень і формуванні понять, що правильно відбивають предмети і явища об’єктивного світу і зв’язок між ними. Ефективність другого етапу залежність не тільки від якості пояснення вчителем, а й від підготовки учнів, їх розвитку, зацікавленості, уваги, та бажання знати те, що пояснює вчитель. (сприймання нового матеріалу спирається на попередній досвід учнів.)
   
3. Етап закріплення вимагає від вчителя індивідуалізованого підходу до учнів.
   

4. Перевірка і оцінювання знань учнів повинні бути пов’язані з усіма ланками навчального процесу, допомагати регулювати всю навчальну роботу.

Виходячи з навчально-виховної мети уроку, вчитель добирає ті або інші джерела набування знань учнями, (зовнішнє оточення, демонстраційне наочне приладдя, дидактичний матеріал, підручник, таблиці ... тощо), враховує специфіку логічних прийомів, за допомогою яких учні оволодівають певними знаннями, вміннями, навичками і залежно від цього визначає методи і, форми використання цих джерел і логічних прийомів для організації навчальної діяльності учнів.

Основними методами-навчання математики у початкових класах: метод, усного викладу, метод вправ, метод лабораторних і практичних робіт, самостійна робота учнів, робота з підручником, метод програмованого навчання, метод проблемного навчання. Значне місце при поясненні нового матері­алу, при формуванні математичних понять посідають індукція і дедукція, аналогія, аналіз і синтез.

Учитель може застосовувати на уроці кілька методів, по-різному поєднуючи їх залежно від навчального матеріалу, мети, структури уроку, віку учнів і їх підготовки. Проте на уроці один із дах методів є провідним, домінуючим він визначає характер навчальної роботи, спря­мованої на досягнення основної мети.

2. Індукція і дедукція. Аналогія, аналіз і синтез.

Спинимося на логічних прийомах і методах, які мають більш загаль­ний характер і свої специфіці особливості в організації та керуванні пізнавальною діяльністю учнів.

▪ Індукція і дедукція.

Вивчаючи математику учень користується різними термінами, означеннями, властивостями дії, залежностями між їх компонентами та результатами і приходить до певних умовиводів. Якщо той або інший умовивід сформульовано в результаті спостережень кількох окремих однотипних властивостей, залежностей, то таку форму розумової діяльності, спрямовану на узагальнення, називаємо індукцією. Готуючись до уроку, учитель, за темою уроку старанно добирає певну кількість відповідних задач і прикладів, тобто ряд окремих математичних фактів, які і будуть вихідним матеріалом для виявлення тих чи інших загальних закономірностей, формування понять, виведення правил, і послідовно у певній системі розміщує їх за своїм поурочним планом ) Наприклад: І клас. “Переставна властивість дії додавання 5+2; 2+5”. На основі математичних фактів учнів роблять висновок: Від перестановки доданків сума не міняється.

Математичні факти

У
Від загального,

до окремого
тісному взаємозв'язку з індукцією застосовується й дедукція. Дедукція - це спосіб міркування від загального до окремого, при якому нове знання про предмет виводиться на основі знання правил і положень, загальних для даного класу предметів і явищ.


Наприклад: 2+7 = 9 - запис у підручнику. Діти, знаючи переставну властивість, усно додають до 7 + 2 бо так легше. До більшого числа прираховують менше (по одиниці). Індукція і дедукція постійно перебувають в органічний єдності.

Задача № 1 Знаходження четвертого пропорційного (з ускладненням) 20:5=4 (грн.) – 1 кв. 4+2=6 (грн.) – 1 кв. 6*7=42 (грн.) – 7 кв.

Задача № 1 Знаходження четвертого пропорційного (без ускладненням) 20:5=4 (грн.) – 1 кв. 4*7=28 (грн.) – 1 кв.

▪ Аналогія. При розв'язуванні окремих задач в разі утруднень вчитель переходить від однієї окремої задачі до однотипної іншої, зрозумілішою для дітей. Учні розв'язують цю задачу, встановлюють схожість її з першою, а потім розв’язують другу задачу.

5 6 5 7




… … - 2 > … …

20 (?) 20 (?)


Під аналізом розуміємо мислений розклад, розчленування об’єкта пізнання на окремі складові частини, елементи з метою кращого уявлення суті цього об’єкта. Щоб потім за допомогою синтезу, тобто сполучення цих елементів, створити повніше уявлення про предмет. Щоб розв'язати задачу треба її спочатку проаналізувати, а потім “синтезувати”.

На І тарілці 5 яблук, на ІІ - на 3 яблука більше. Скільки яблук на двох тарілках?

І
? - Аналіз

І
- Синтез
І

5+3+5=13 (ябл.) – на двох тарілках

Відповідь: 13 яблук

Аналіз і синтез у навчанні - логічні прийоми. Оскільки мислення людини являє собою аналітико-синтетичну діяльність головного мозку, то аналіз і синтез так само як індукція і дедукція, також органічно пов’язані між собою і пронизують собою весь навчальний процес,

3. Метод усного викладу. Пояснення вчителя. Бесіда.

Існують різні форт пояснення: бесіда, розповідь, лекція. У початкових класах здебільшого використовують форму бесіди, рідше розповідь і лекції. Бесіда є методом керування навчальною діяльністю учнів, у процесі якої вони відповідають на запитання вчителя, і з його допомогою підсумовують свою роботу. Цільові завдання бесіда найрізноманітніші,

4. Метод вправ, письмових і графічних робіт.

Часто буває, що учень робить у контрольній роботі помилки в обчисленнях, чи при розв'язуванні задач, або учень не встигає виконати до кінця контрольну роботу бо надто повільно обчислює. Причина цього в тому, що мало розв’язано вправ на закріплення вив­ченого, мало приділено уваги повторенню.

Тобто мало виконано практичних вправ на ту чи іншу тему. Для цього потрібно виконати достатню кількість вправ. Уміння ї навички закріплюються і до деякої міри автоматизуються.

Разом з міцними навичками безпомилкового виконання дій над абстрактними й іменованими числами, учні початкових класів повинні набувати також, і графічних навичок, що має велике значення в підготовці їх до практичної діяльності. Наприклад за допомогою графічних схем учні розв'язують задачі на рух, рівняння.


5. Самостійна робота учнів. Робота з підручником.

Самостійна робота як метод навчання дає можливість учневі свідомо і міцно засвоїти матеріал, проявити розумову активність.

Найчастіше метод самостійних робіт застосовують при ознайомленні з питанням практичного характеру, коли учні самостійно знаходять на основі здобутих знань нові обчислювальні прийоми, нові способи розв'я­зування задач тощо.


6. Метод лабораторних робіт.

Особливе значення його при вивченні геометричного матеріалу.

Вже з І класу діти практично ознайомлюються з одиницями довжини, ваги, часу, площі, швидкості, об’єму і способами їх вимірювання.

Процес вивчення геометричного матеріалу на уроках математики в початкових класах повинен бути від початку до кінця активним, наочним, конкретним. Роботи можуть бути такі: креслення» вирізування, виготовлення геометричних фігур. Під керівництвом вчителя учні навча­ються працювати з лінійкою, косинцем, циркулем, рулеткою, набувають елементарних навичок креслення і вимірювання, користування палеткою.

Лабораторна робота розраховується на цілий урок після пояснення вчи­телем теми. Клас ділиться на групи по 6-8 учнів у кожній групі. 1 кожній групі дасться завдання.


7. Метод програмованого навчання.

Одним з нових методів навчання, при якому можна здійснити інди­відуалізоване навчання і постійний контроль за сприйманням та засвоєнням нових знань учнями, є програмове навчання.

Суть програмового навчання полягає в тому, що навчальний матеріал розділяють на невеликі частини, які розмішують у певній послідовності. Кожен учень вивчає навчальний матеріал індивідуально, за своїм темпом, виявляючи при цьому найбільший ступінь самостійності.

Програмове навчання ділять на “машинне” і “безмашинне”. При “безмашинному” програмованому навчанні складають спеціальний програмований підручник.


8. Проблемний метод навчання.

Одним з найефективніших шляхів розвитку творчих розумових здібностей учнів є проблемне навчання. При такому навчанні перед учнями на уроці ставлять проблемні питання, на які вони самостійно знаходять відповіді. Наприклад, тема уроку (3 клас). “Ділення складеного іменованого числа на просте іменоване число”.

Урок починається з повторення матеріалу, необхідного для засвоєння нового. Далі вчитель ставить перед учнями проблему. Наша школа запланувала відправити до міста робітникам заводу (шефам) Іт 5ц. яблук. Ми повинні розрахувати, скільки треба заготовити ящиків, щоб у кожний ящик вміщалося 25 кг яблук.

1. 1т 5ц = 1500 кг – перетворення складного іменованого числа у просте іменоване число

2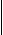. 1т 5ц : 25 кг = – вчимось записувати вирази

1500 25

150 60

0


3. Діти роблять висновки.

Висновок: щоб справитись з такою проблемою треба навчитись перетворювати складене іменоване число у просте іменоване число, а ділення простих іменованих чисел виконуємо, як ділення абстрактних чисел. Цей метод демонструє зв’язок з життям.


Запитання і завдання до теми:

1. Сформулювати основні вимоги до методів навчання математики.
   
2. Охарактеризувати суть і особливості індукції і дедукції як методів наукового пізнання і методів навчання.
   
3. В чому суть логічних прийомів навчання – аналізу і синтезу?
   
4. Як спрямовується самостійна робота учнів над підручниками?
   
5. Висвітлити особливе значення лабораторного методу при вивченні геометричного матеріалу.
   
6. У чому суть програмованого навчання і яке місце його при вивченні математики в початкових класах?
   
7. В чому суть проблемного методу навчання? Навести приклад проблемного підходу до з’ясування якогось питання з математики в одному з початкових класів.
   

ТЕМА №3.

Засоби навчання математики. Наочні посібники з математики їх види і особливості використання.

Мета вивчення: познайомити студентів з основними та додатковими засобами навчання математики, навчальними посібниками для учнів та вчителів, навчити вміло використовувати їх при підготовці до уроку.

Література: [3,7,13,15,18,19].

Обладнання: демонстраційні та індивідуальні таблиці. Комплект підручників математики 1 - 4 кл., абак, палетка, відеозапис уроку з математики.