Исследование переходных процессов в замкнутых нелинейных системах управления 111

Вид материала

Исследование

Содержание Лабораторная работа n11 исследование качества регулирования в замкнутых линейных системах при случайных воздействиях 130 Лабораторная работа n9 исследование переходных процессов в замкнутых нелинейных системах управления Порядок выполнения работы Теоретические сведения Контрольные вопросы Содержание отчета Лабораторная работа n10 исследование автоколебательных процессов в замкнутых нелинейных системах приближенными методами Порядок выполнения работы Теоретические сведения Пример выполнения Контрольные вопросы Содержание отчета Лабораторная работа n11 исследование качества регулирования в замкнутых линейных системах при случайных воздействиях Порядок выполнения работы Теоретические сведения Пример моделирования случайных процессов в линейных системах Контрольные вопросы Содержание отчета

Подобный материал:

• Вторая Международная научная конференция моделирование нелинейных процессов и систем, 145.53kb.
• Лабораторная работа №1 2 исследование переходных процессов, 92.12kb.
• Природа явлений в нелинейных цепях гораздо сложнее и многообразнее чем в линейных, 149.95kb.
• Расчет параметров автоколебательных процессов в нелинейных системах автоматического, 442.41kb.
• О новом поколении компьютерных лабораторных практикумов по электрофизике, 9.71kb.
• Применение среды labview для исследования переходных процессов в нелинейных цепях, 52.55kb.
• Моделирование переходных электромеханических процессов в пвк анарэс, 55.75kb.
• Переходные процессы в электрических системах рабочая программа, методические указания., 137.38kb.
• Лекция №4. Операторный метод расчета переходных процессов, 59.84kb.
• Курс: Регулярная и хаотическая динамика нелинейных систем, 278.41kb.

ЛАБОРАТОРНАЯ РАБОТА N9 ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЗАМКНУТЫХ НЕЛИНЕЙНЫХ СИСТЕМАХ УПРАВЛЕНИЯ

Цели работы: закрепление теоретических сведений по динамике систем с нелинейными звеньями, приобретение навыков исследования процессов в нелинейных замкнутых системах автоматического управления и оценки их устойчивости по фазовым траекториям.

Порядок выполнения работы

Для объекта с передаточными функциями (6.1) – (6.3), заданного преподавателем, ПИД-регулятора с передаточной функцией

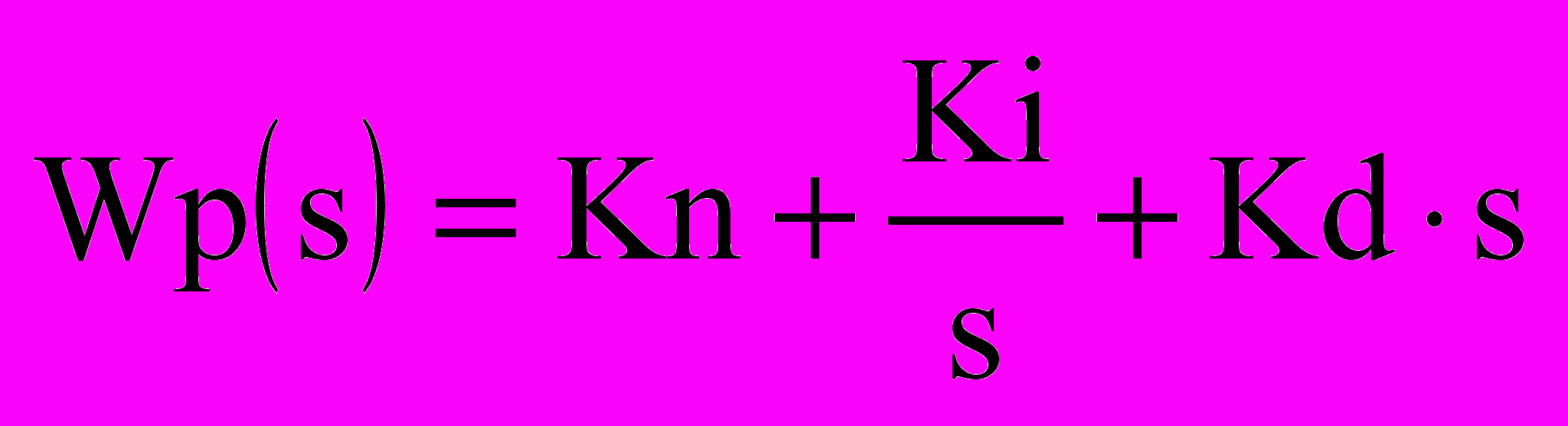(8.1)

и нелинейного звена (см. рис.8.1-8.5) провести исследование влияния коэффициентов регулятора и параметров нелинейного звена на характер переходных процессов и фазовые портреты замкнутой системы.

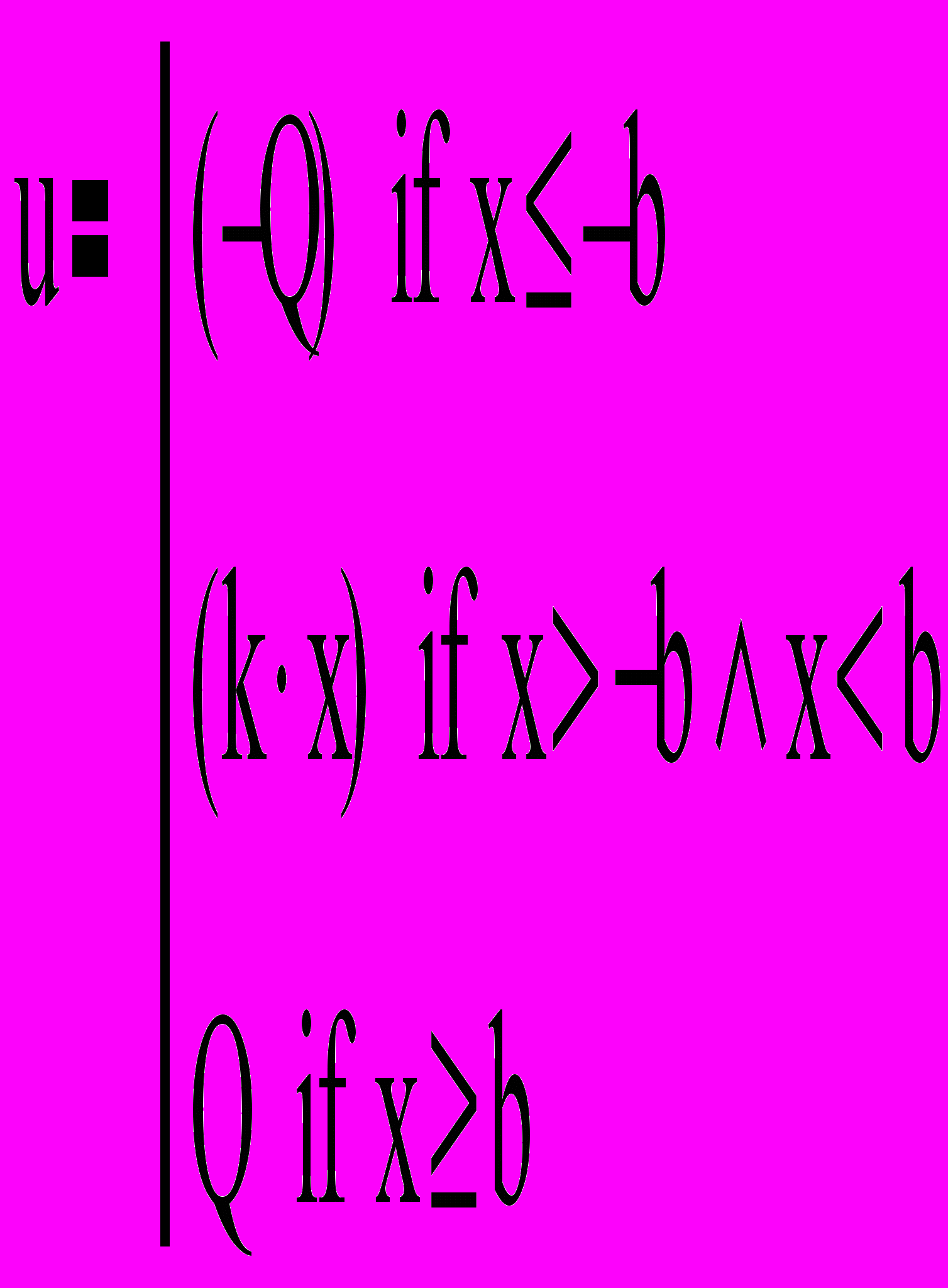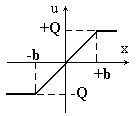
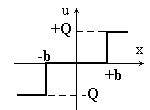
Рис.8.1. Звено насыщения
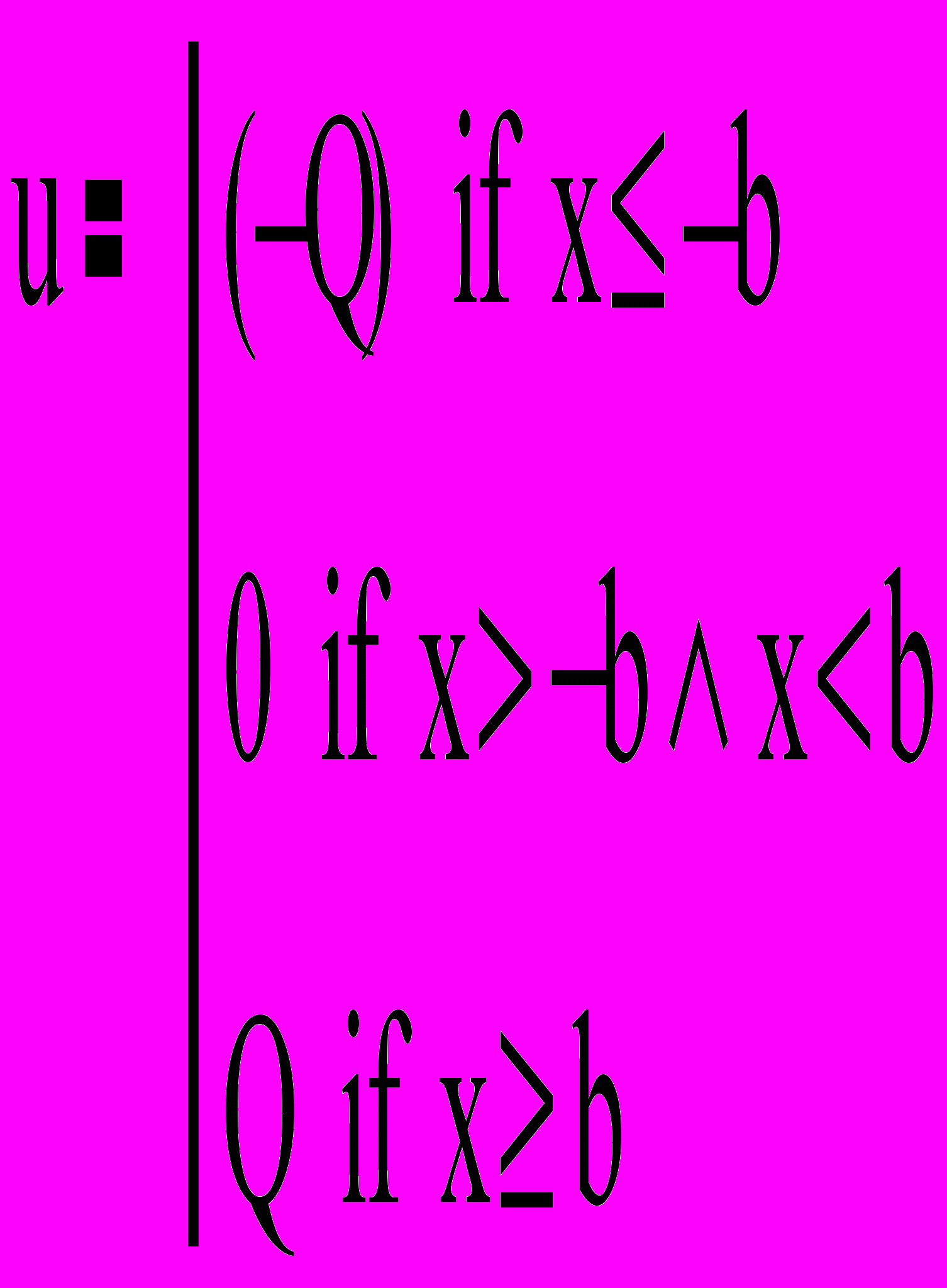Рис.8.2.Идеальное трехпозиционное реле

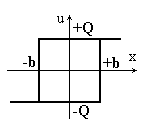
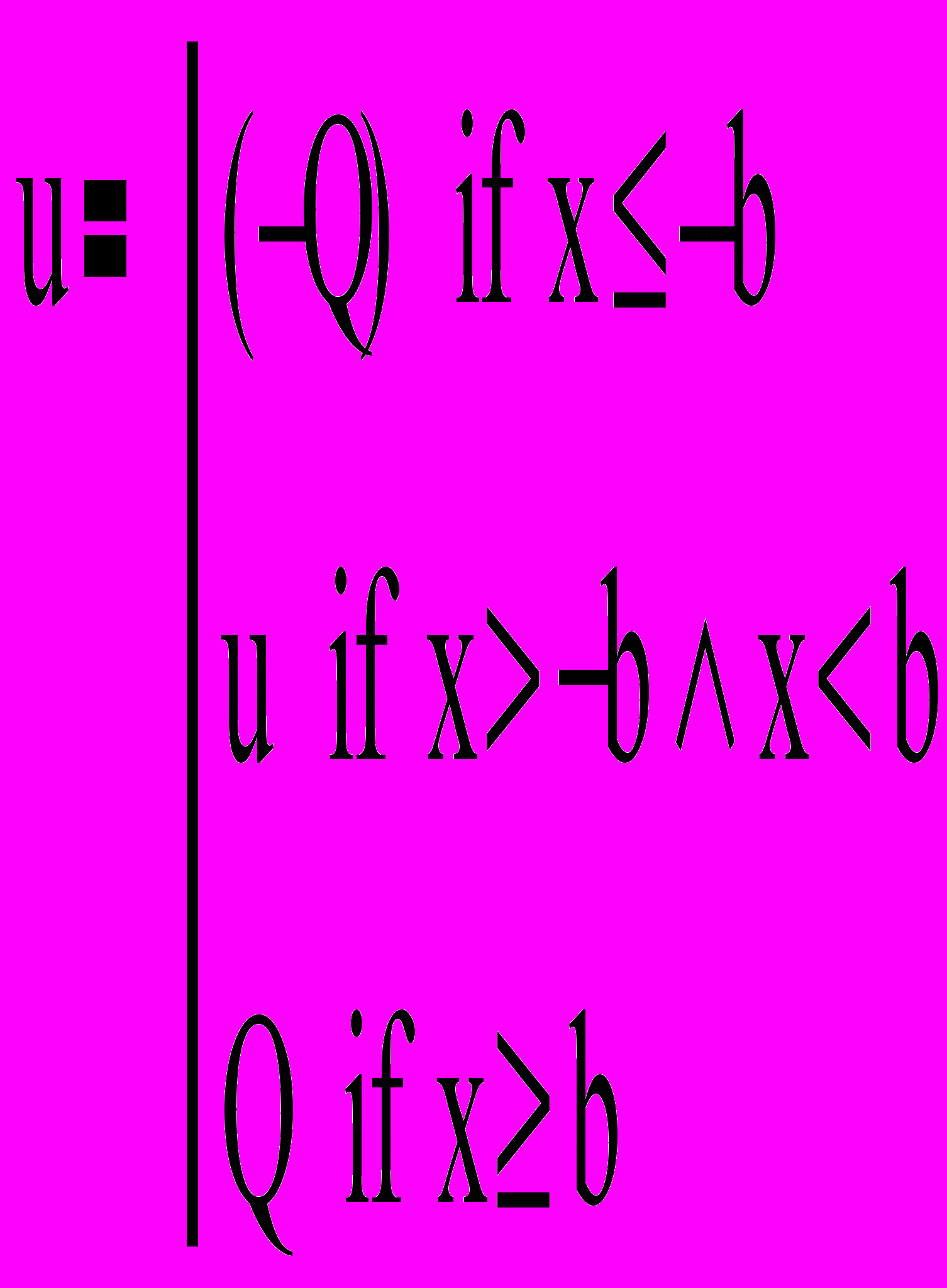
Рис.8.3. Двухпозиционное реле с зоной нечувствительности



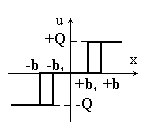
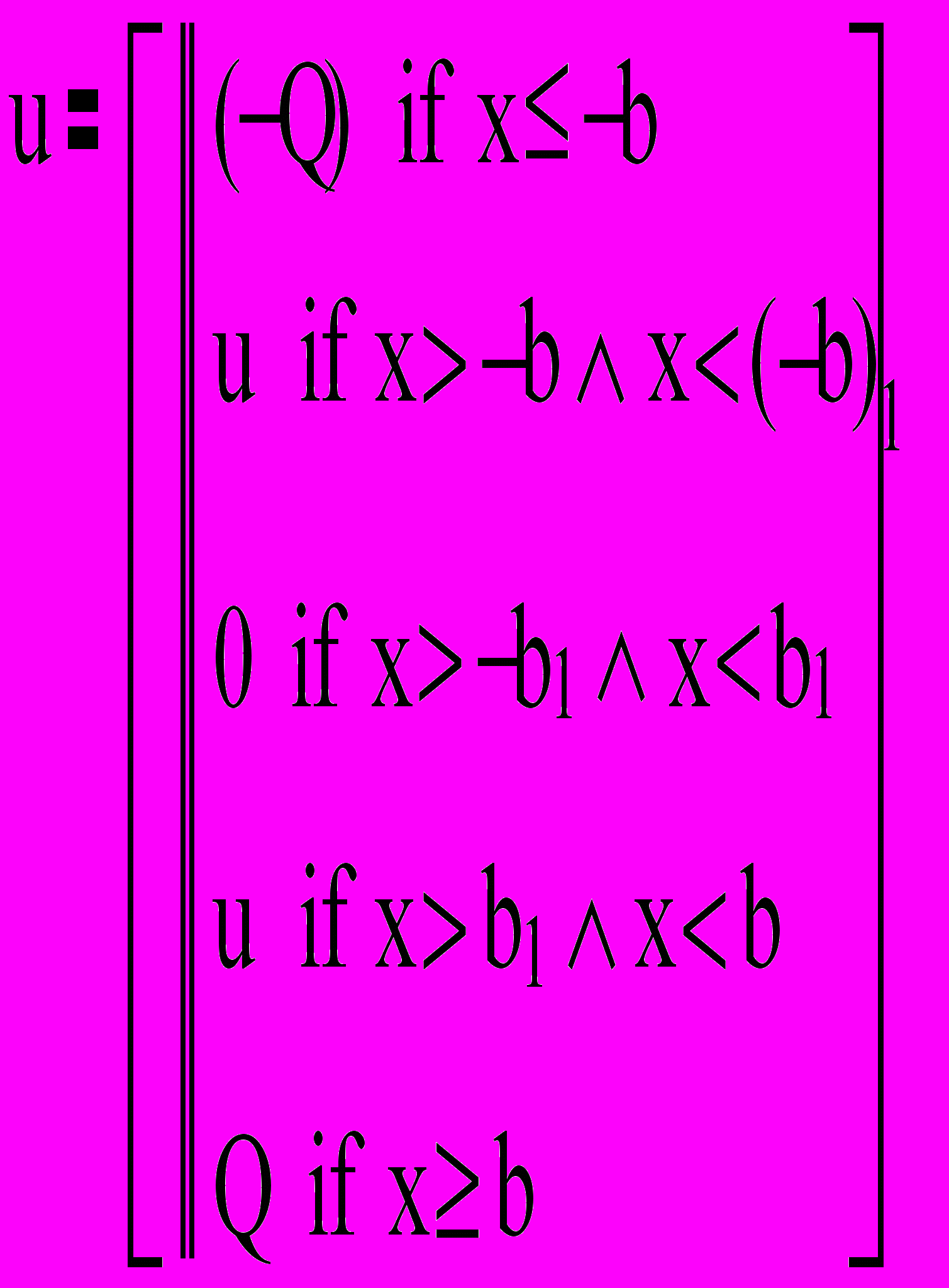
Рис.8.4. Трехпозиционное реле с зоной нечувствительности



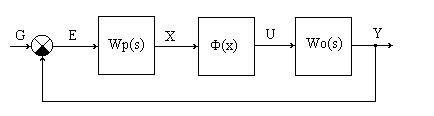
Рис.8.5. Структурная схема нелинейной замкнутой системы

Теоретические сведения

При исследовании замкнутых систем автоматического регулирования с нелинейными звеньями обычно составляют систему уравнений, которую решают аналитически или численно.

Так для схемы рис.8.5 с ПИД-регулятором, апериодическим звеном второго порядка и нелинейным звеном с характеристикой рис. 8.3 система уравнений имеет следующий вид:









Во временной области система может быть записана как:









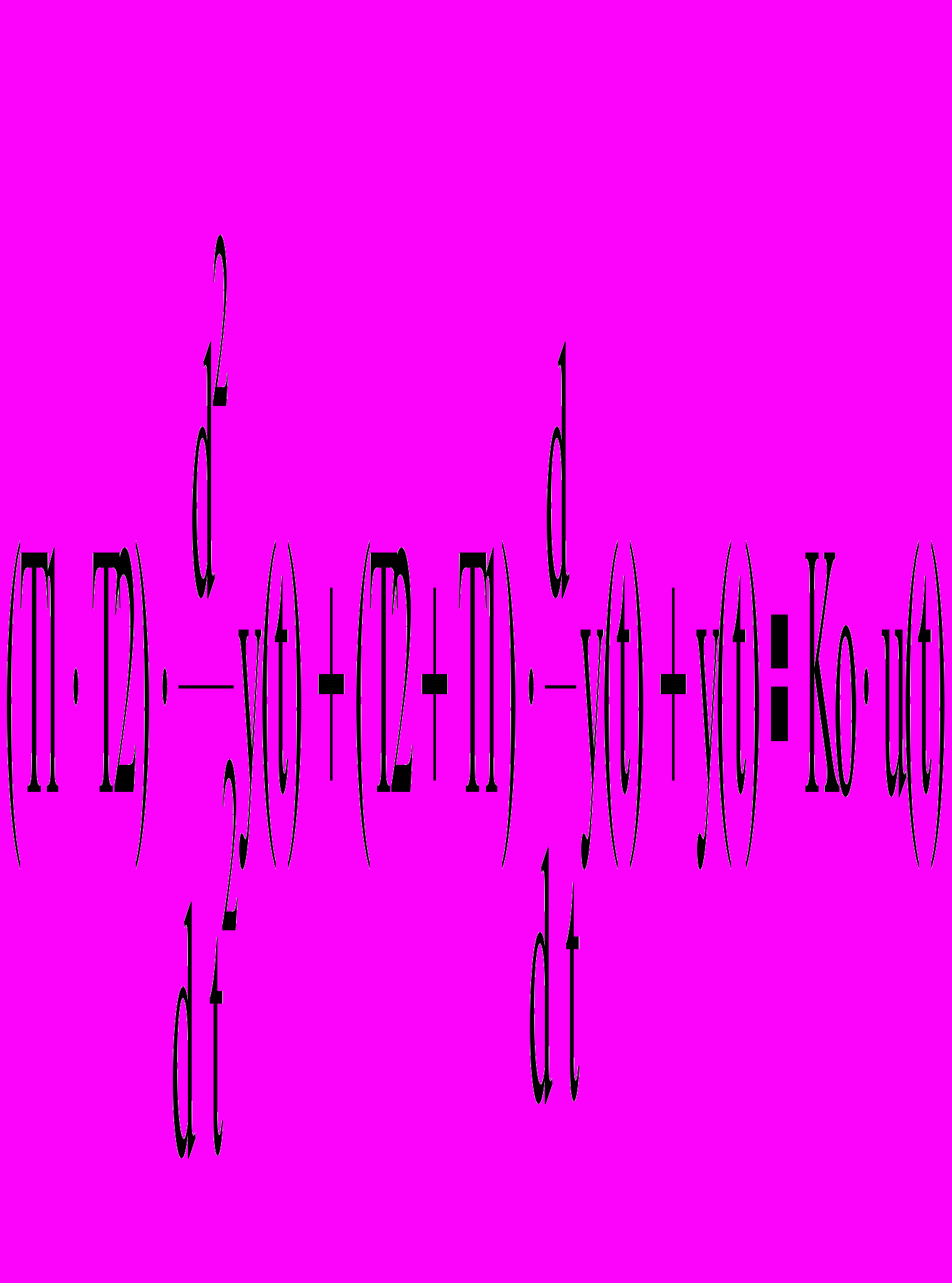
Для решения системы уравнений можно перейти к конечным разностям.









Решать систему конечно-разностных уравнений при соответствующих параметрах и начальных условиях можно с помощью программного блока, занося все результаты в матрицу А, например:








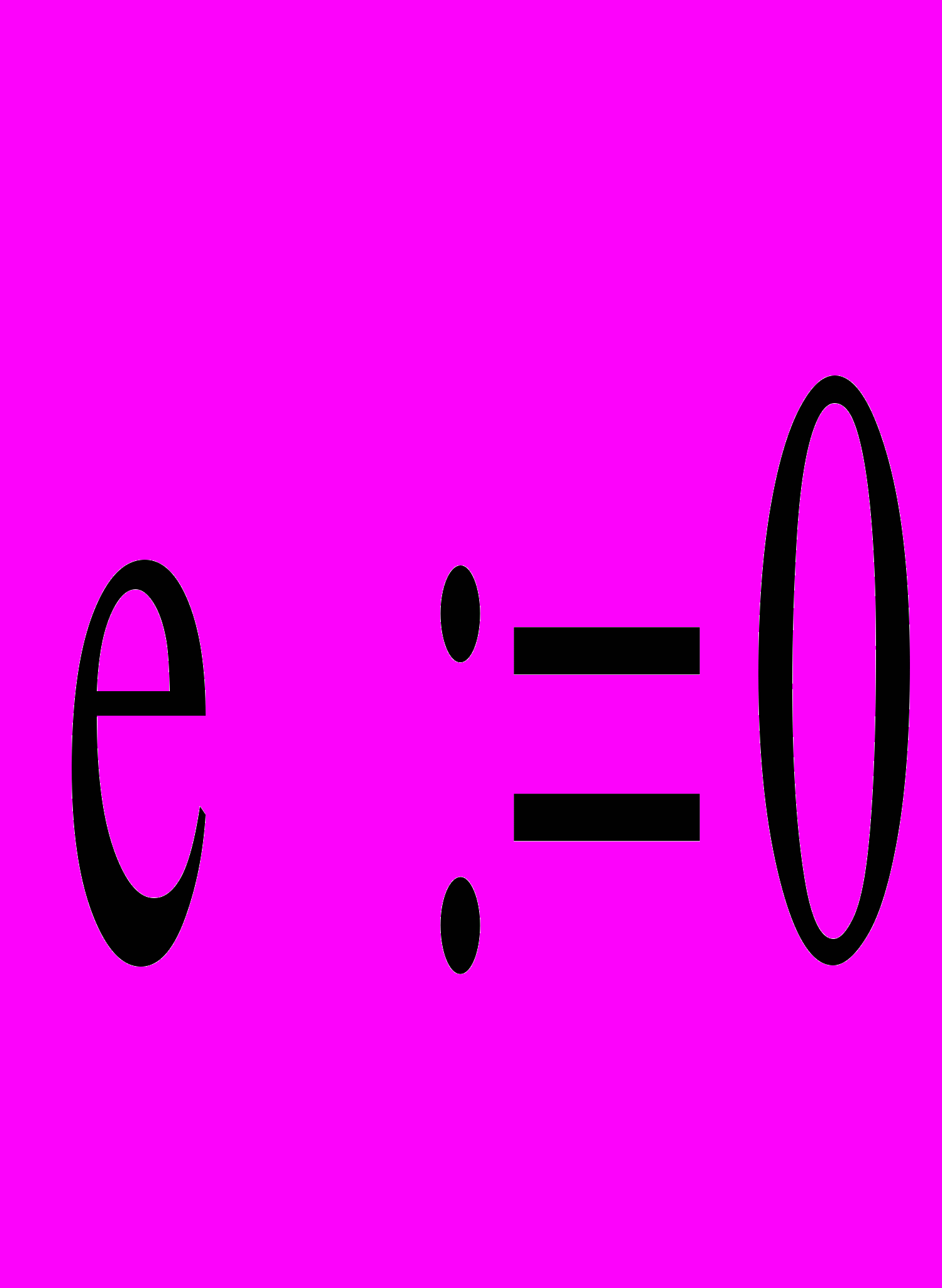
Для постоянных параметров объекта и нелинейного звена в описание функции эти параметры можно не включать.

О

бращение к функции вычисления переходных процессов производится оператором присваивания

Поскольку вычисления производились со второй точки, начало матрицы следует заполнить начальными значениями





_{Т
аблица расчетов приведена ниже, причем, в первую колонку занесены значения у, во вторую – е, в третью – х, и в четвертую – u.}

i
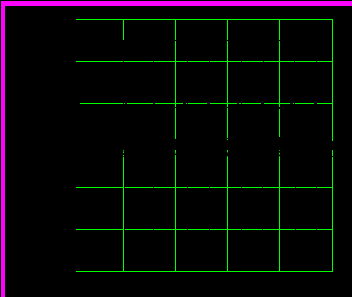
:=2..1000

Рис.8.6. Графики переходных процессов для соответствующих сигналов

Для построения фазовой траектории приближенное значение производной можно вычислить по формуле

Ф
азовая траектория для указанных выше начальных условий: имеет вид:

Р
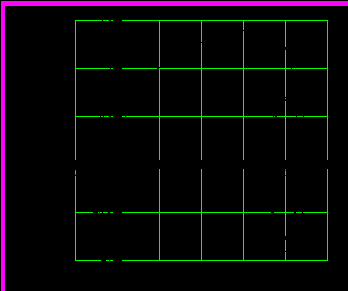
ис.8.7.Фазовая траектория для замкнутой системы

_{Для другого набора параметров регулятора моделирование проводится аналогичным образом.}