Geum.ru

Исследование переходных процессов в замкнутых нелинейных системах управления 111

Вид материалаИсследование

Содержание


Лабораторная работа n10 исследование автоколебательных процессов в замкнутых нелинейных системах приближенными методами
Порядок выполнения работы
Теоретические сведения
Подобный материал:
1   2   3   4   5   6

ЛАБОРАТОРНАЯ РАБОТА N10 ИССЛЕДОВАНИЕ АВТОКОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ В ЗАМКНУТЫХ НЕЛИНЕЙНЫХ СИСТЕМАХ ПРИБЛИЖЕННЫМИ МЕТОДАМИ


Цели работы: закрепление теоретических сведений по динамике систем с нелинейными звеньями, приобретение навыков исследования автоколебательных процессов в нелинейных замкнутых системах автоматического управления методами гармонического баланса или гармонической линеаризации.

Порядок выполнения работы


Для схемы и исходных данных лабораторной работы N8 получить комплексную характеристику нелинейного звена.

Для трех различных наборов параметров регулятора и нелинейного звена методами гармонического баланса или гармонической линеаризации оценить возможность возникновения устойчивых автоколебаний при нулевом задании, определить частоту автоколебаний и амплитуду сигнала х1 (рис. 9.1).



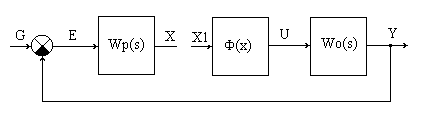
Рис.9.1. Структурная схема условно разомкнутой системы

Используя программу лабораторной работы N8 построить переходные процессы для 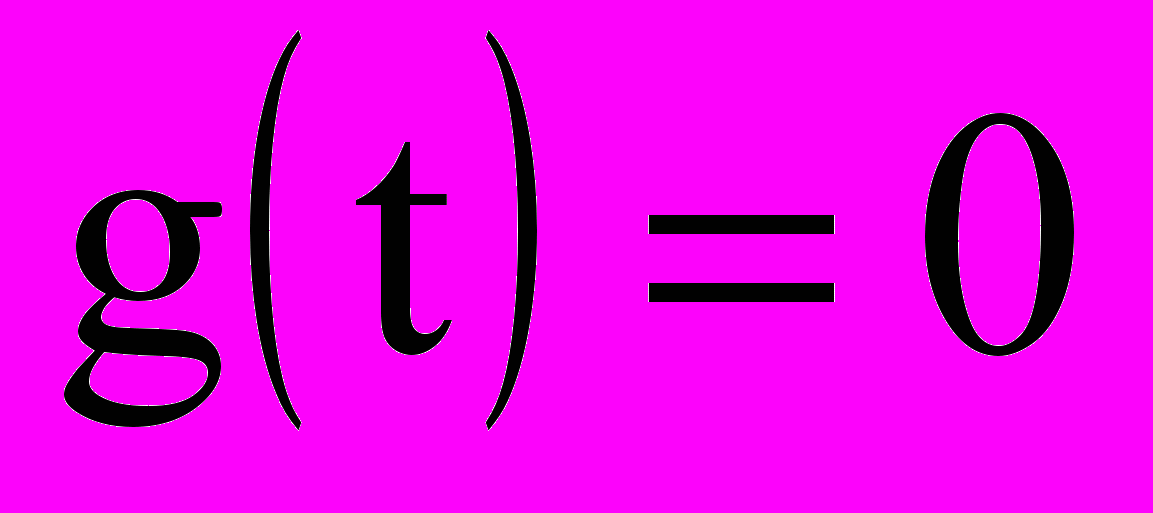и определить частоту колебаний (если они возникают) и амплитуду сигнала х. Сравнить их с вычисленными в предыдущем пункте.

Теоретические сведения

Метод гармонического баланса


В общем случае условие возникновения автоколебаний в замкнутой нелинейной системе формулируется следующим образом: если гармонический сигнал при прохождении через разомкнутую систему сохраняет амплитуду (баланс амплитуд), а фазу изменяет на 180о (баланс фаз), то при замыкании такой системы в ней возникнут автоколебания. Для системы (рис.8.1), разомкнутой перед нелинейным звеном (рис.9.1), условие возникновения автоколебаний будет записано как:

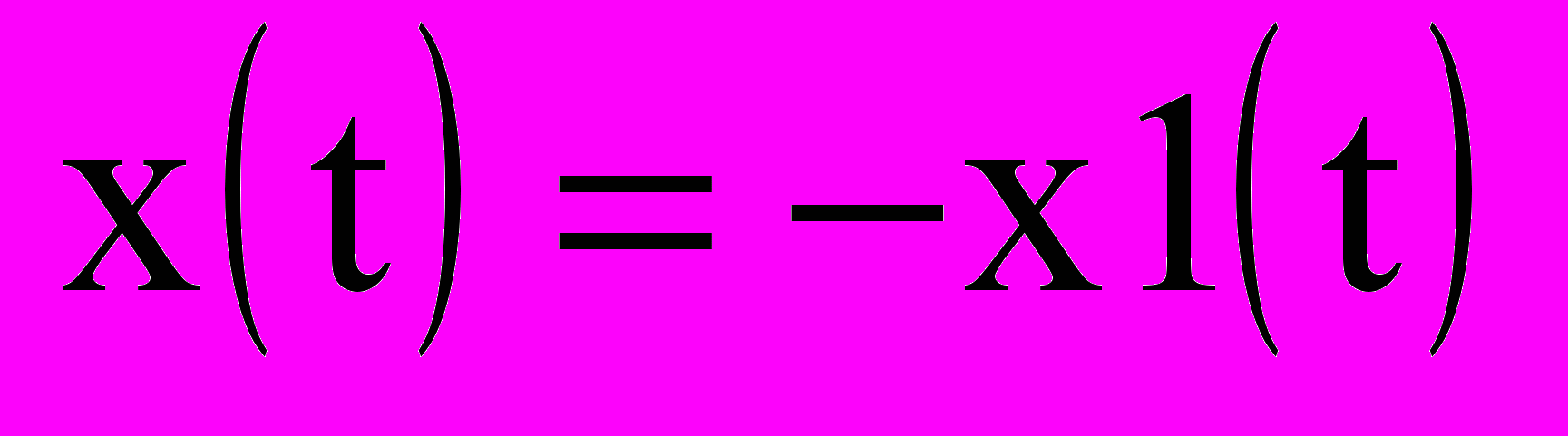(9.1)

и 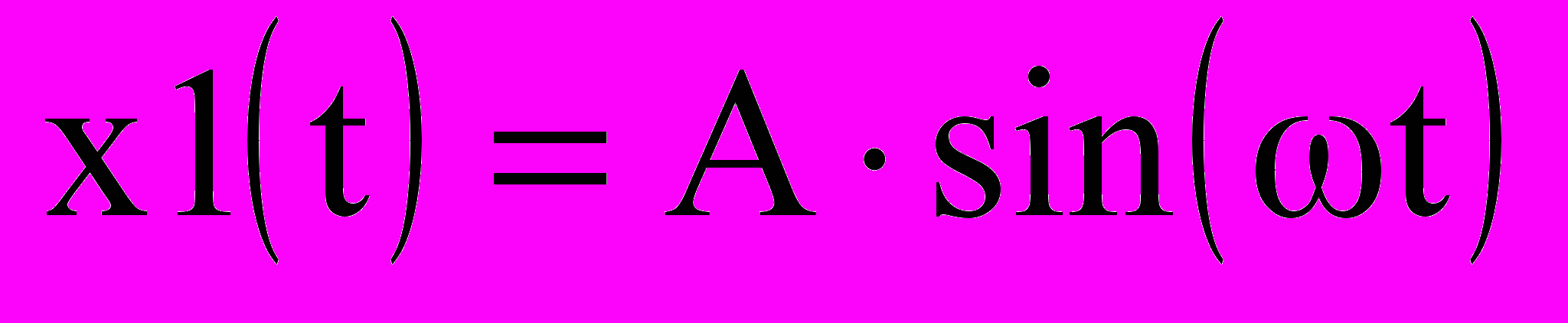. (9.2)

Чтобы проверить выполнение условия возникновения автоколебаний в конкретной системе, например, с нелинейной функцией представленной на рис. 8.3, необходимо перейти от сигналов к параметрам системы, используя ее математическое описание:



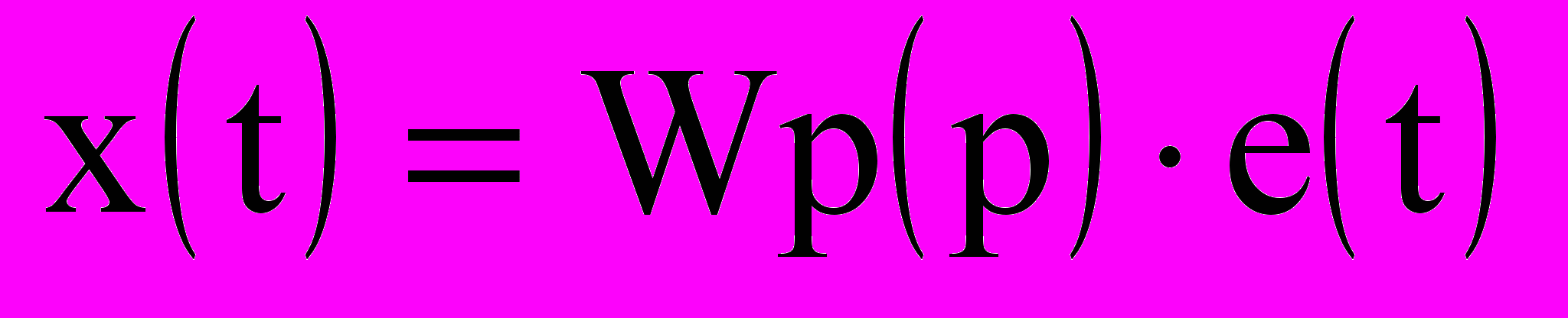
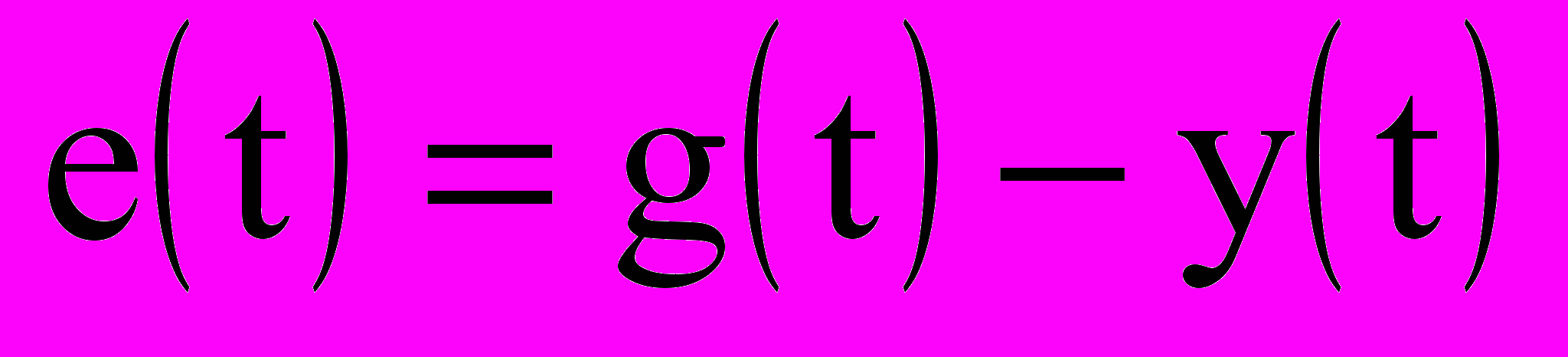(9.3)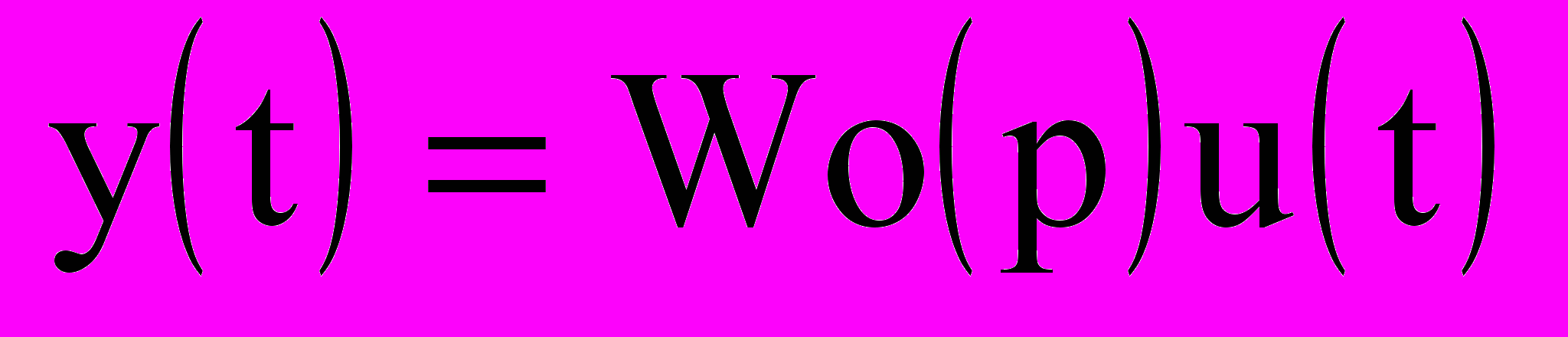





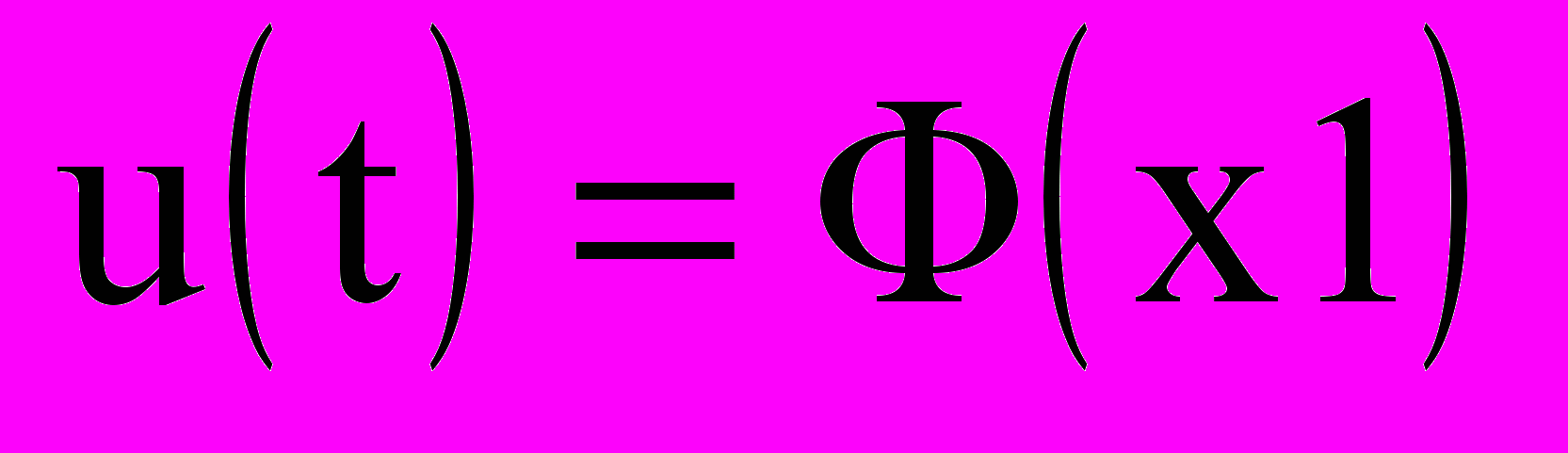
где Wр(p) и Wо(p) - передаточные функции регулятора и объекта управления в операторной форме, Ф(х1) - функция нелинейного преобразования сигнала х1(t).

При подаче на вход нелинейного звена разомкнутой системы гармонического сигнала х1(t) с амплитудой A>b, на выходе нелинейного звена (см.рис.8.4) сформируется периодический импульсный сигнал u с прямоугольными импульсами (рис.9.2), период следования которых совпадает с периодом входного гармонического сигнала.



Рис. 9.2. Сигналы на входе и выходе нелинейного звена

Управляющий сигнал u можно представить в виде суммы гармонических сигналов ( ряда Фурье):

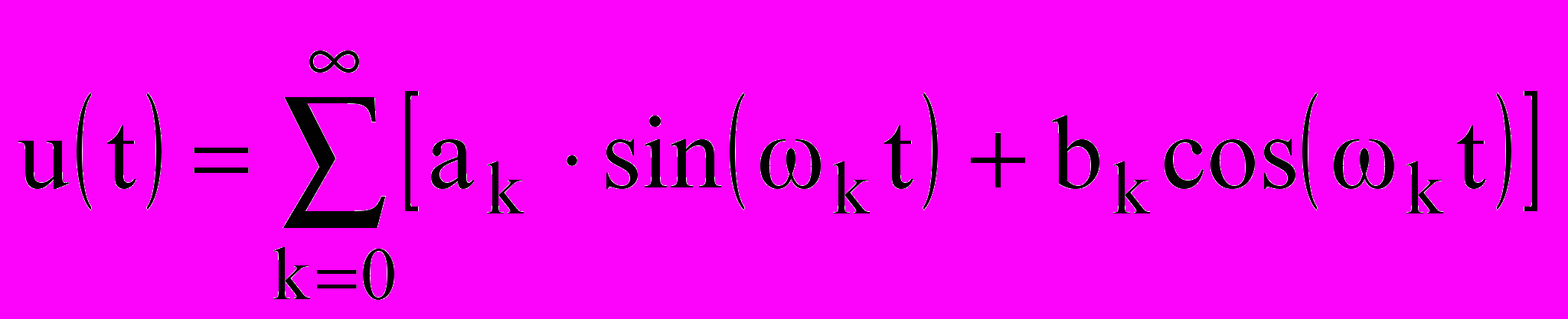, (9.4)

где ak и bk - коэффициенты ряда Фурье, вычисляемые как:


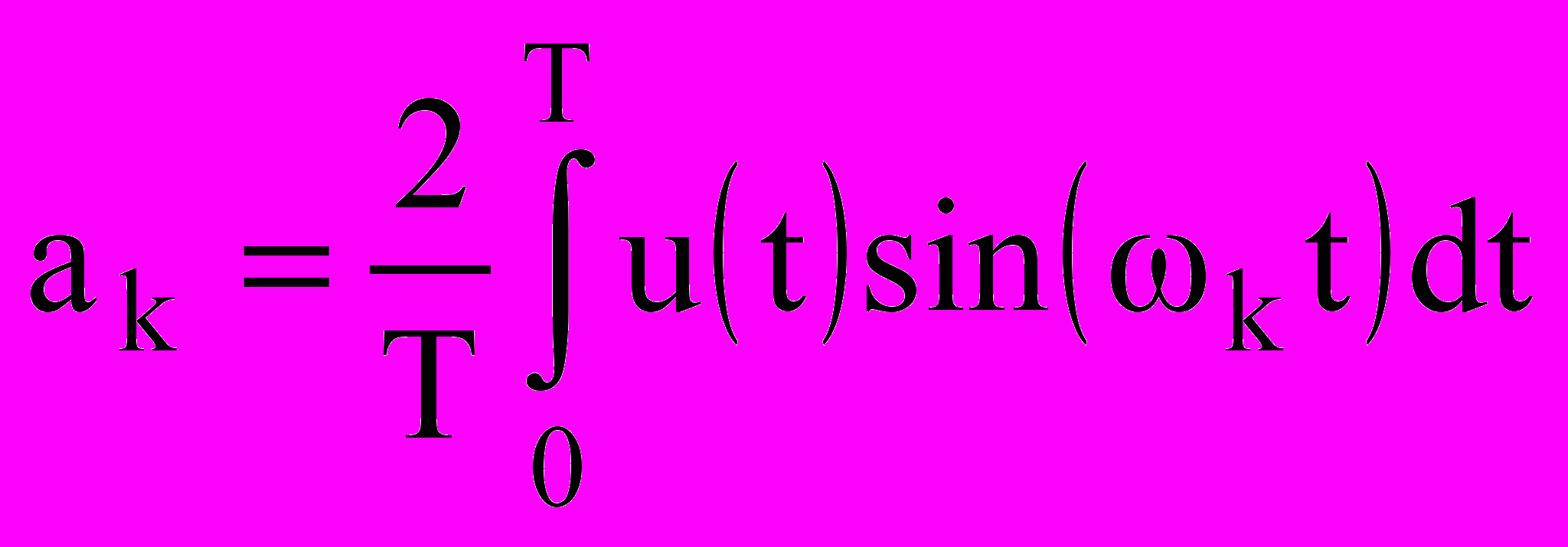, k=1, 2, ... (9.5)

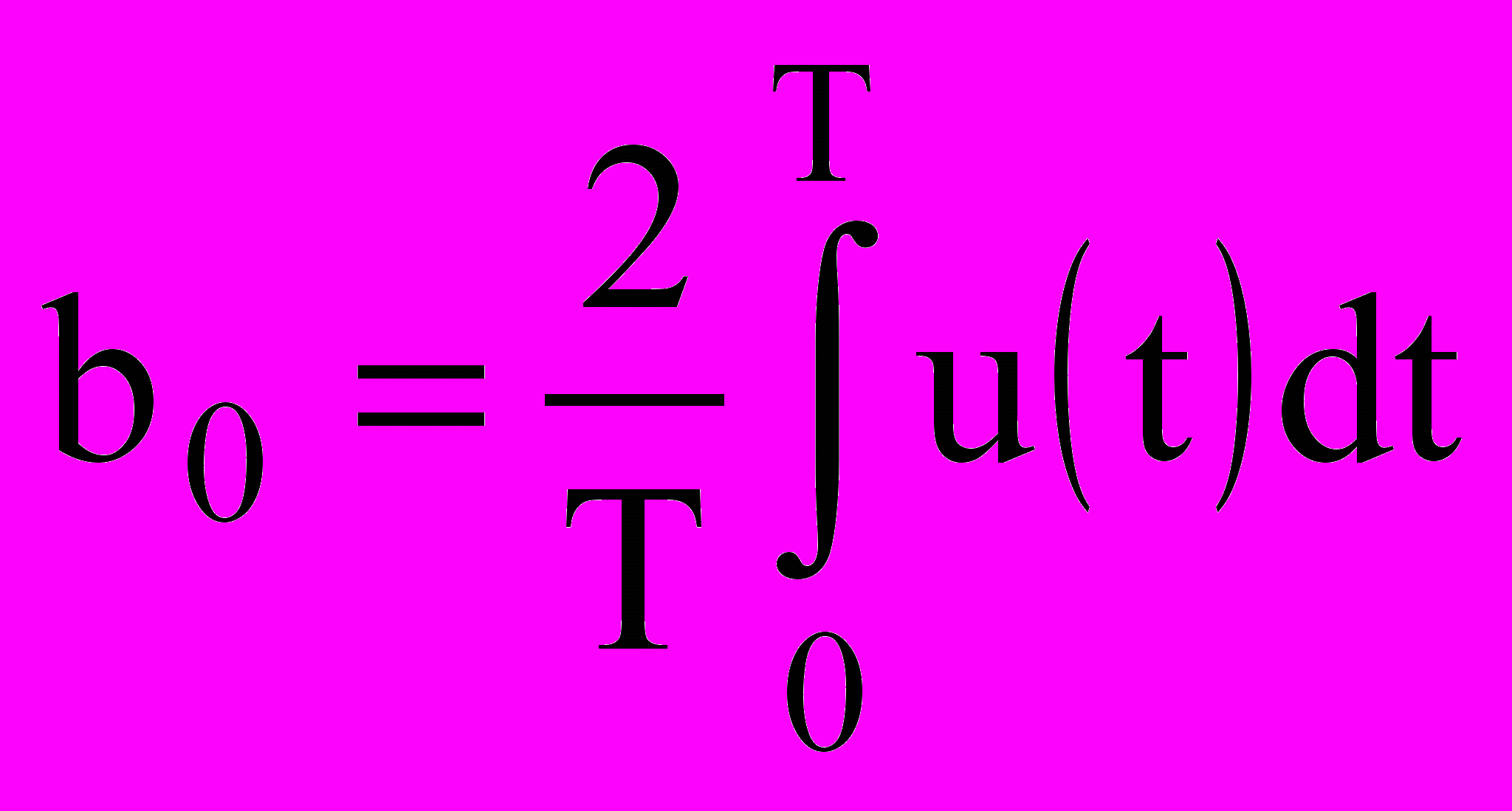, (9.6)

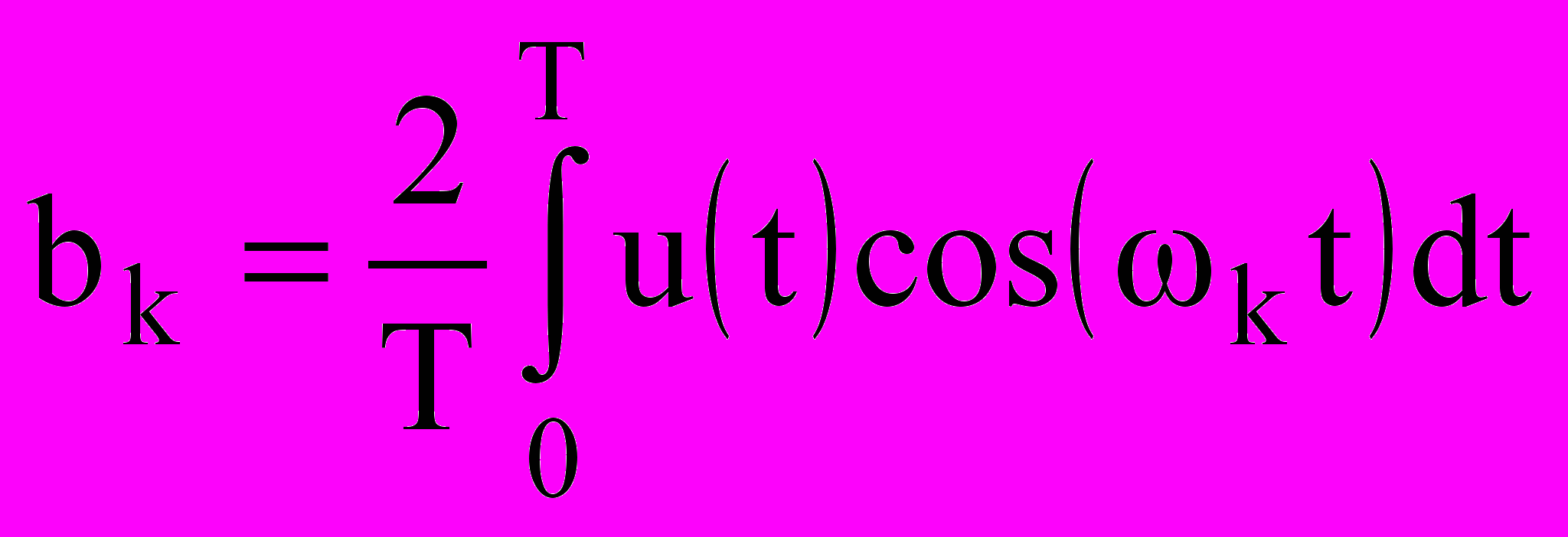, k=1, 2 ... (9.7)

k - частота k-й гармоники, равная 2k/T, T - длительность интервала разложения функции, равная периоду повторения сигнала Т= 2/.

Если линейные звенья системы выполняют фильтрацию низких частот сигнала, то при прохождении сигналом этих звеньев амплитуды гармоник сигнала u, частоты которых выше частоты среза АЧХ звеньев, будут уменьшены по сравнению с первой гармоникой. Вследствие этого, с определенной степенью точности, можно ограничится анализом изменения амплитуды и фазы только первой (основной) гармоники, приняв

,

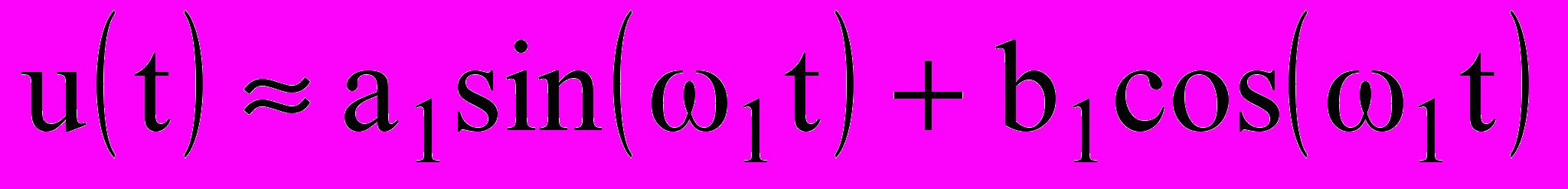или 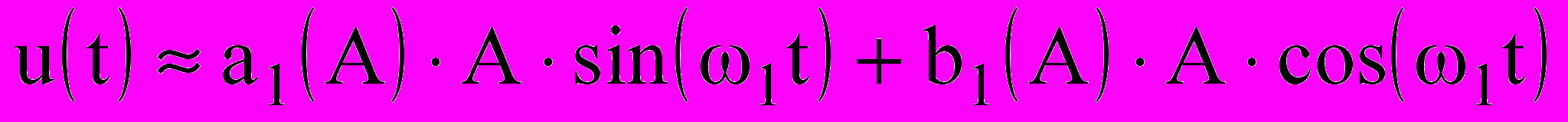, (9.8)

где a1(A) =a1/А , b1(A) = b1/A.

Выражение (9.8) можно переписать как

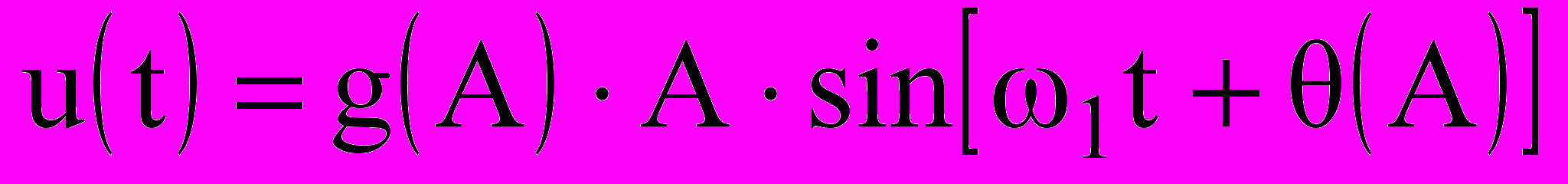, (9.9)

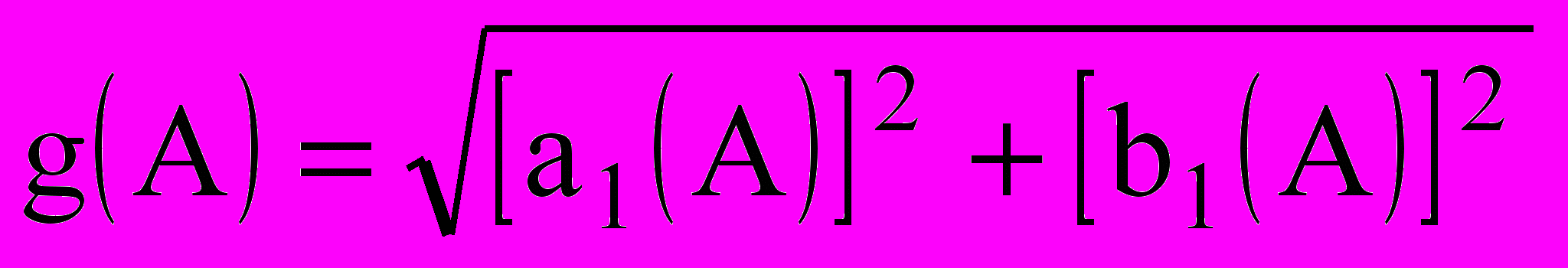, (9.10)

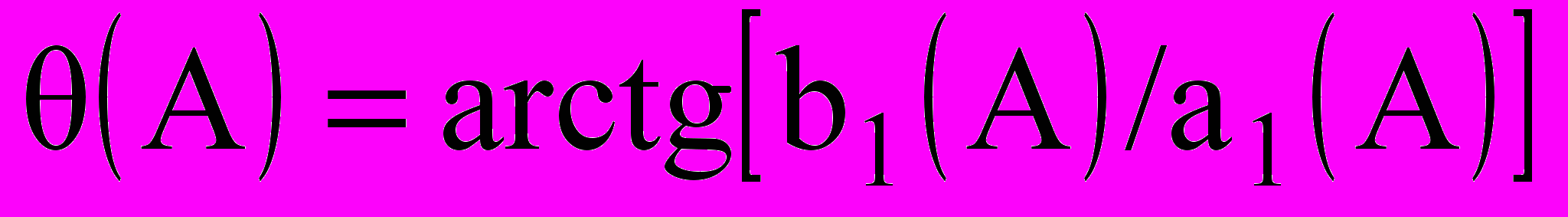. (9.11)

По аналогии с линейными системами, функции g(A) и (A) можно считать модулем и фазой некоторой комплексной характеристики нелинейного звена,

J (A)= g(A)exp[j(A)] = a1(A) + jb1(A), (9.12)

эквивалентной частотной характеристике или передаточной функции линейной системы. Сигнал на выходе нелинейного элемента с учетом сказанного будет равен u = J (A)х1.

Коэффициенты a1(A) и b1(A) в соответствии с (9.5), (9.7) пр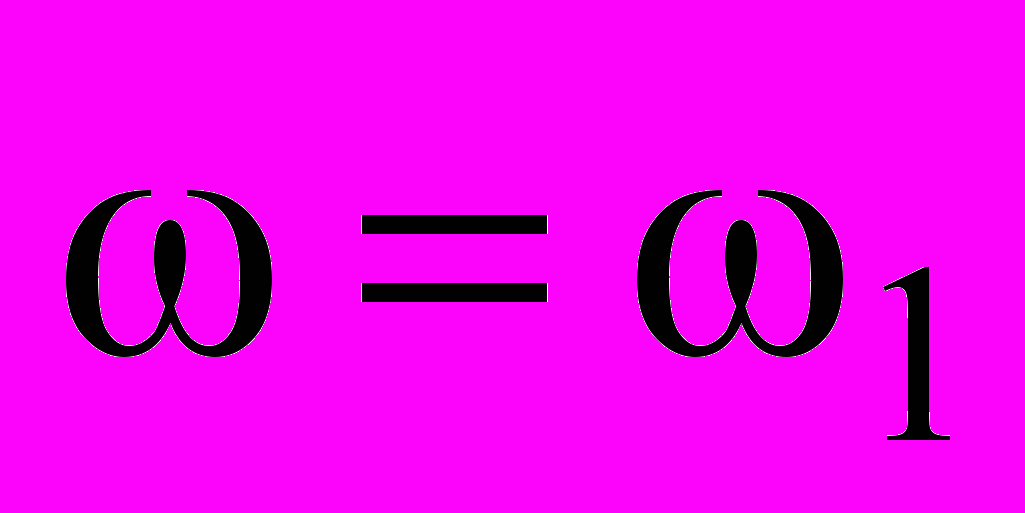и и 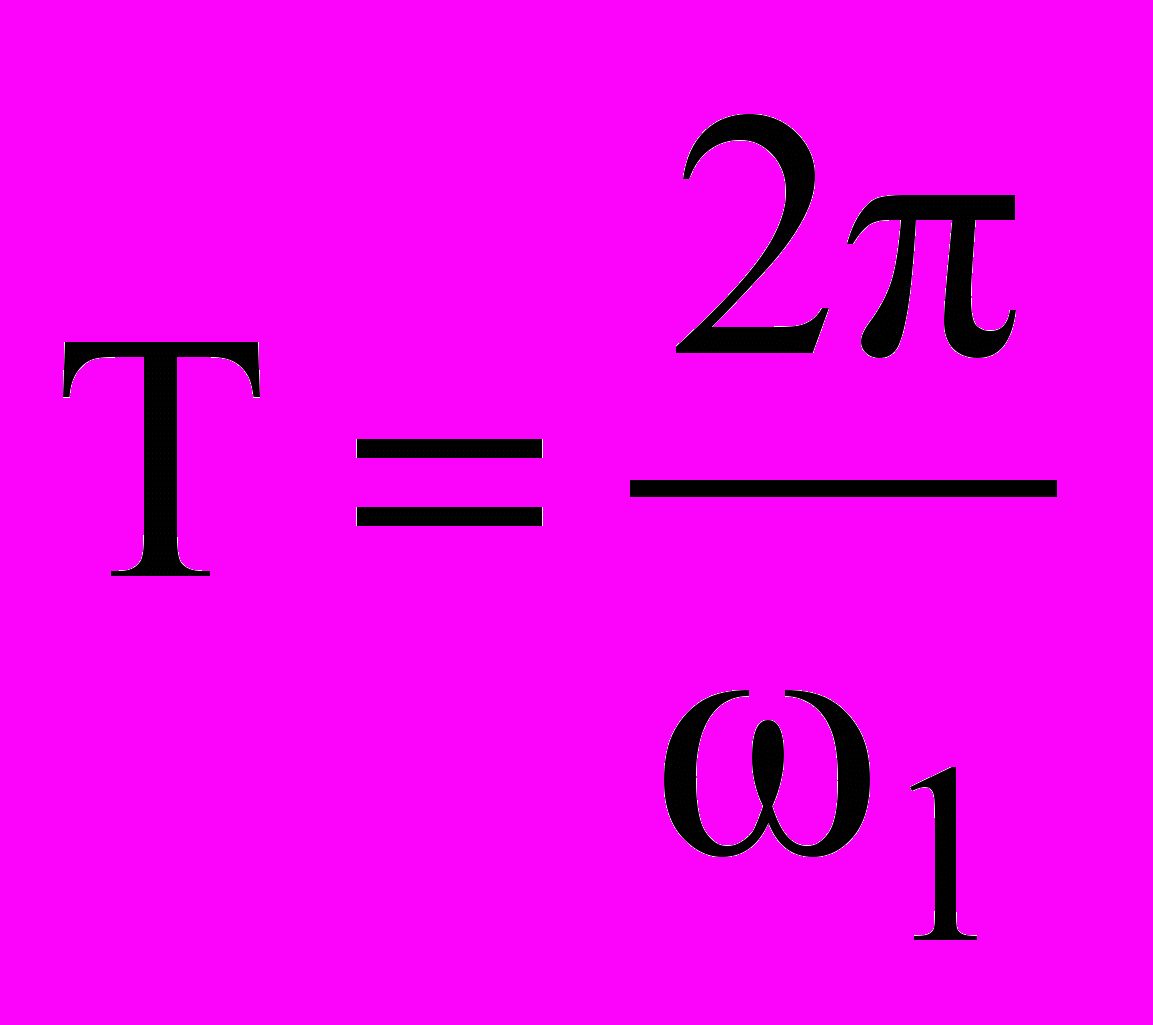могут быть записаны как:

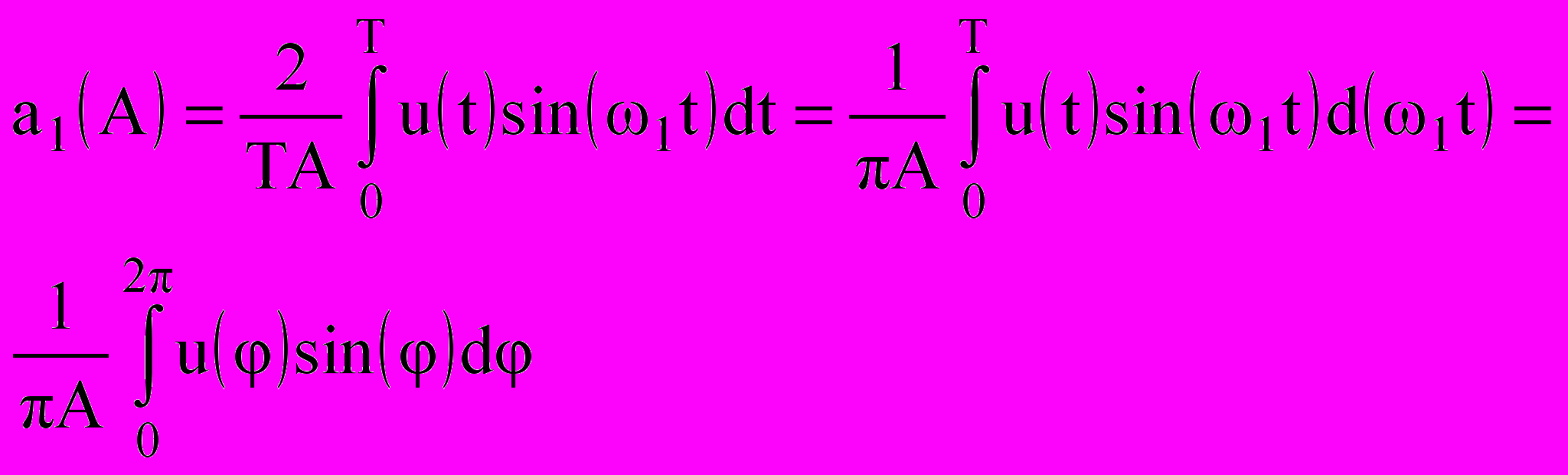, (9.13)

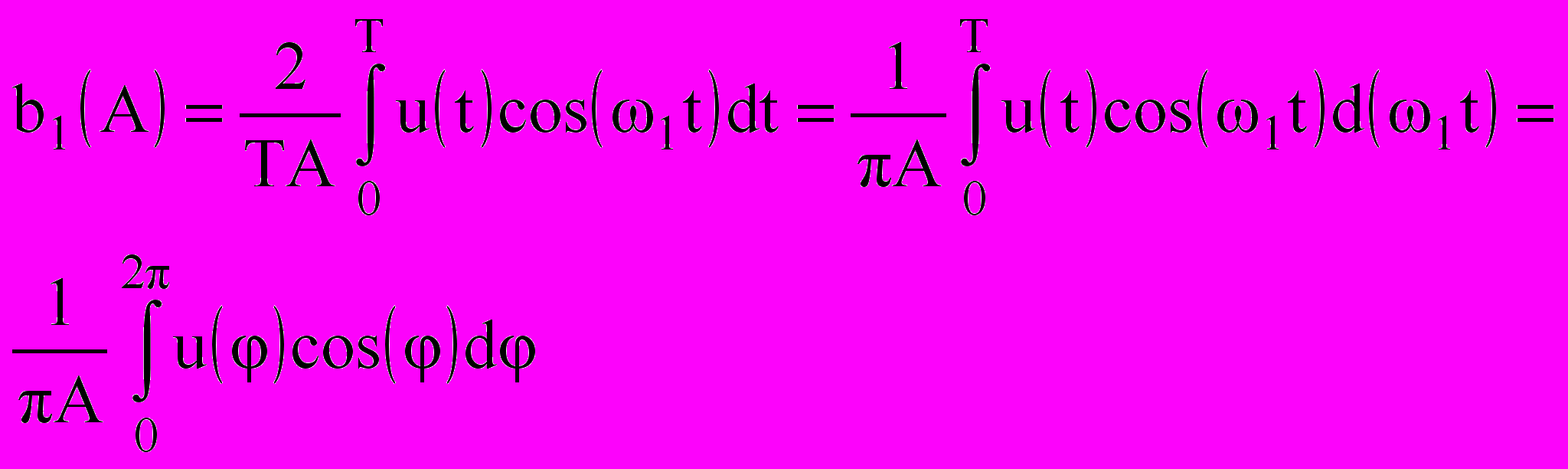, (9.14)

где - фазовый угол гармонического сигнала, равный .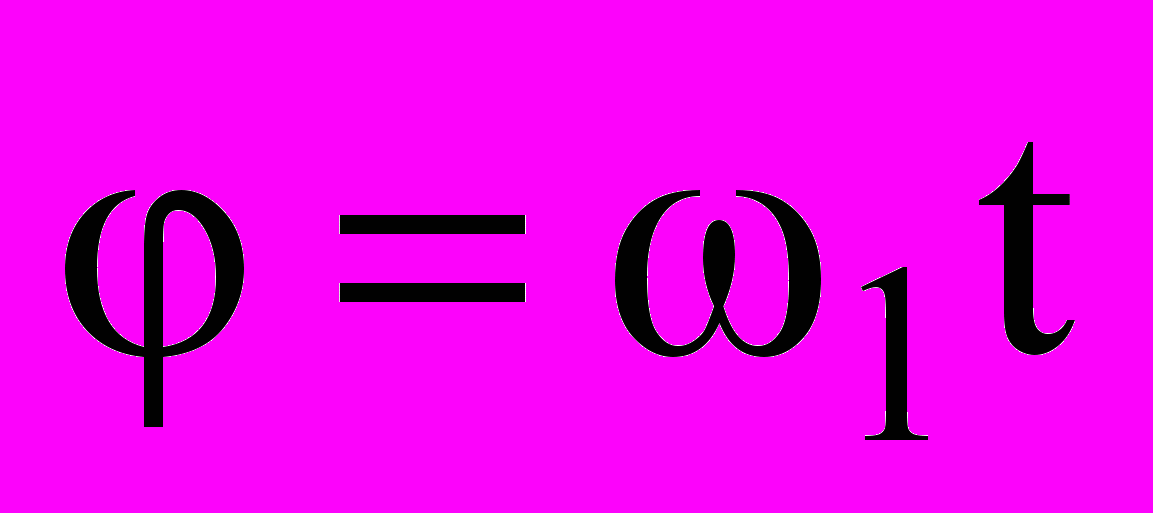

Так как 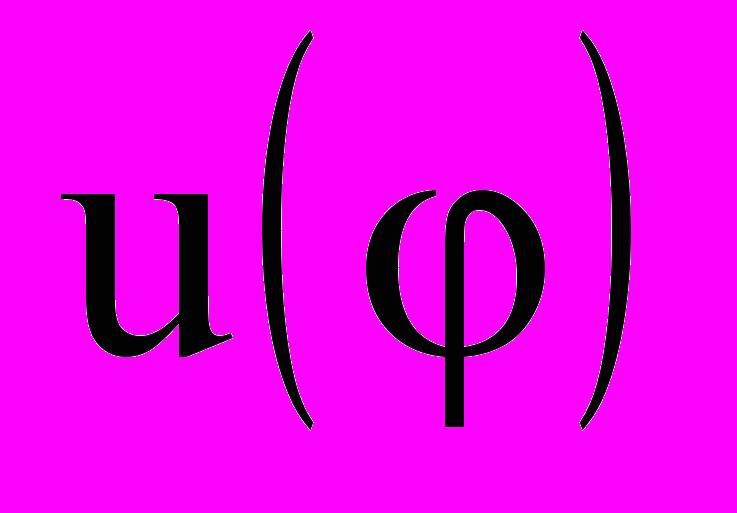принимает постоянные значения на участках 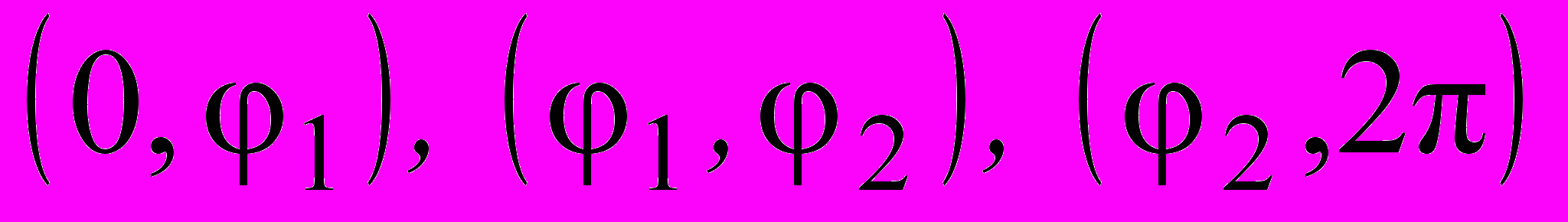, интегралы (9.13), (9.14) представляются суммами интегралов от элементарных функций косинуса и синуса для этих участков:

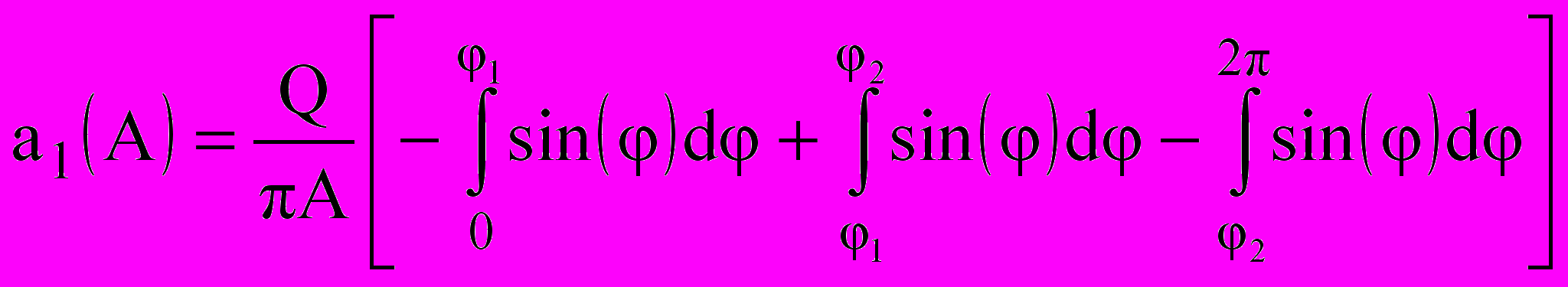, (9.15)

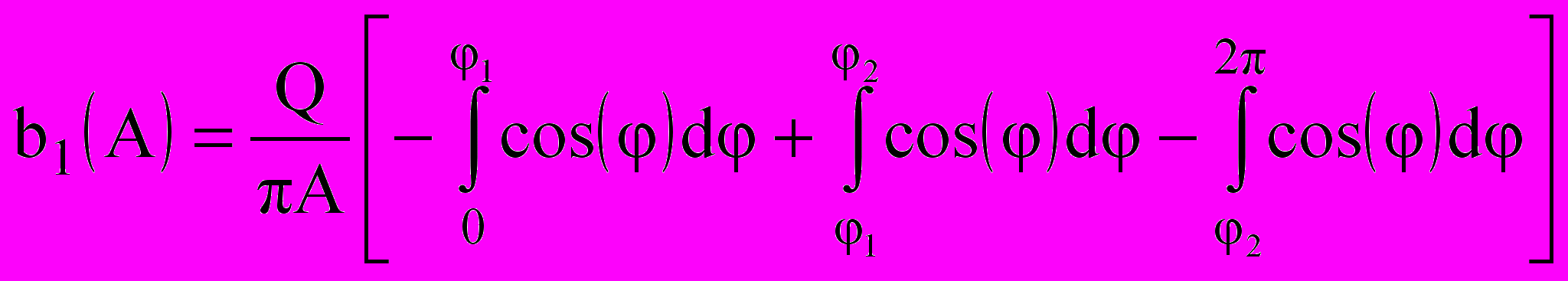, 9.16)

а 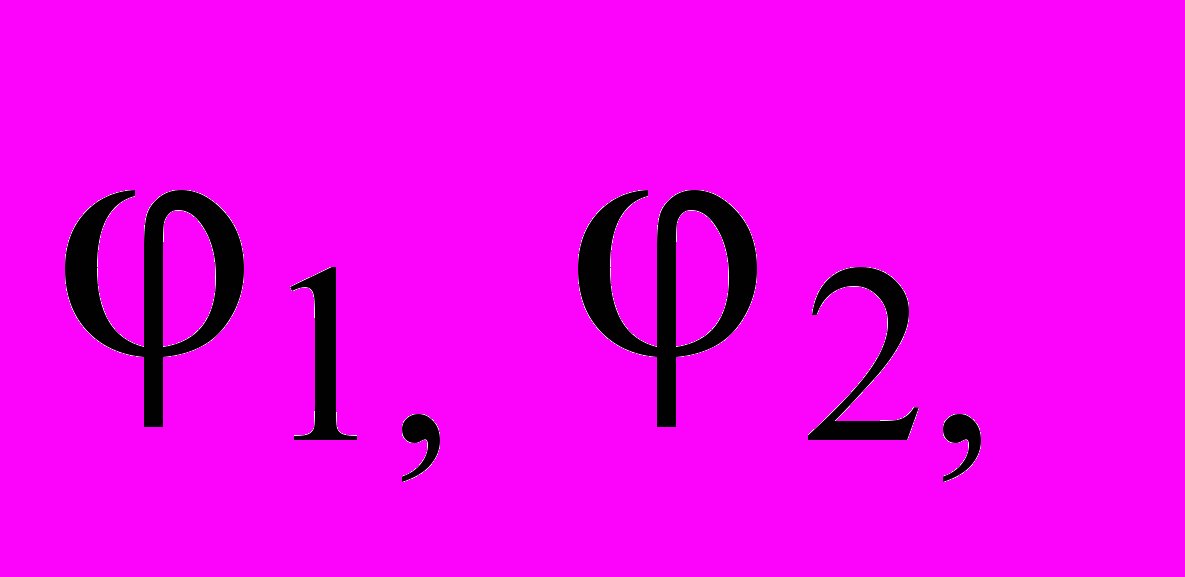определяются из условия достижения входным гармоническим сигналом x1 пороговых уровней переключения -b и +b , т.е.

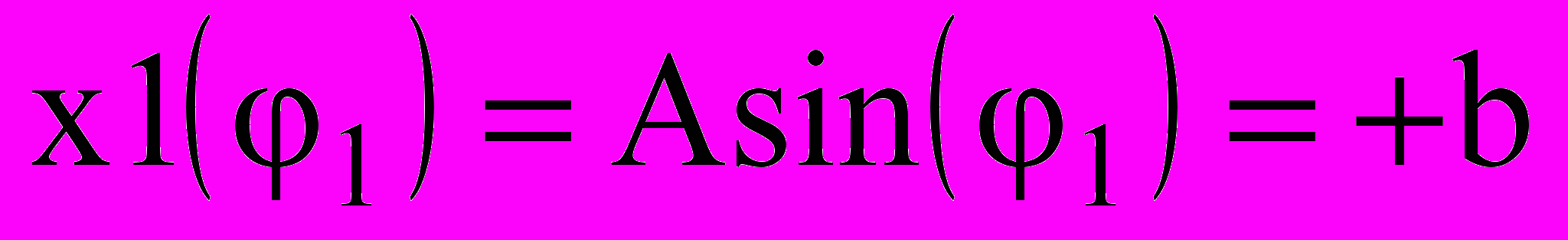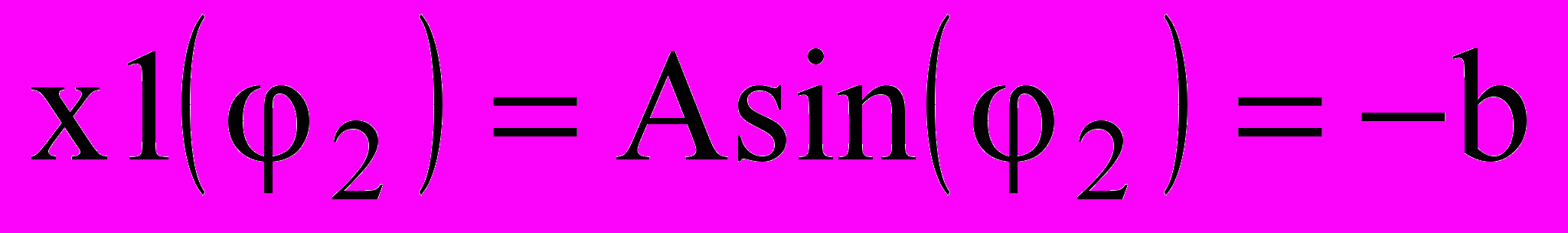и или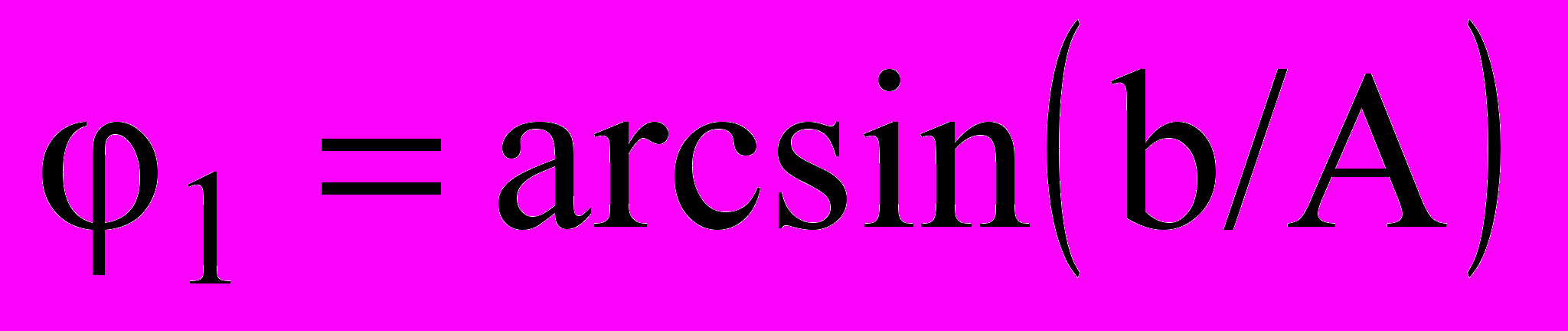

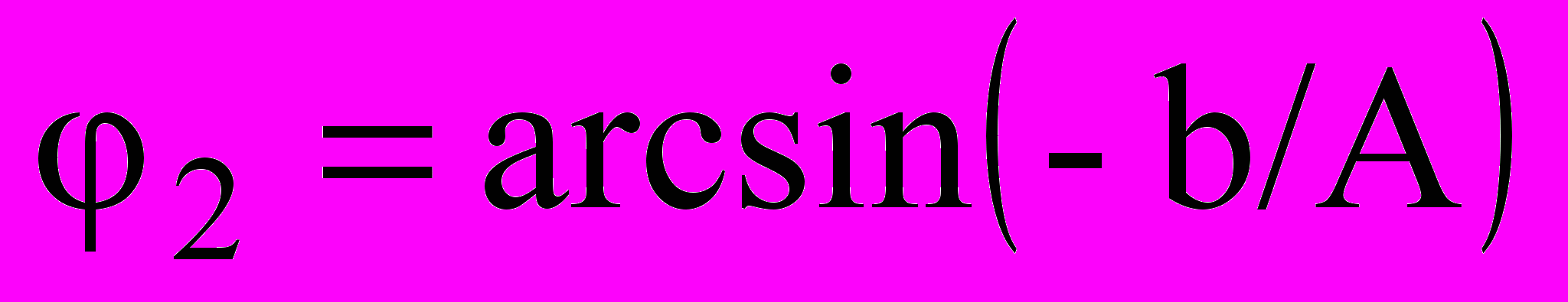, . (9.17)

Коэффициенты a1(A), b1(A) с учетом выражений (9.17)равны

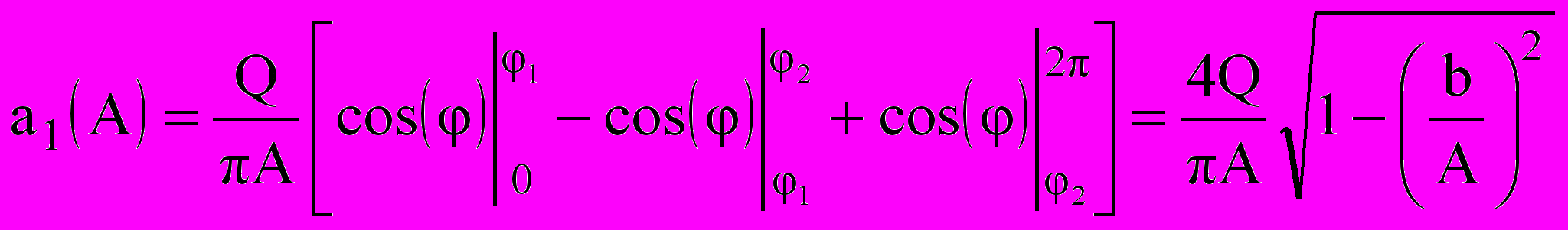,(9.18)

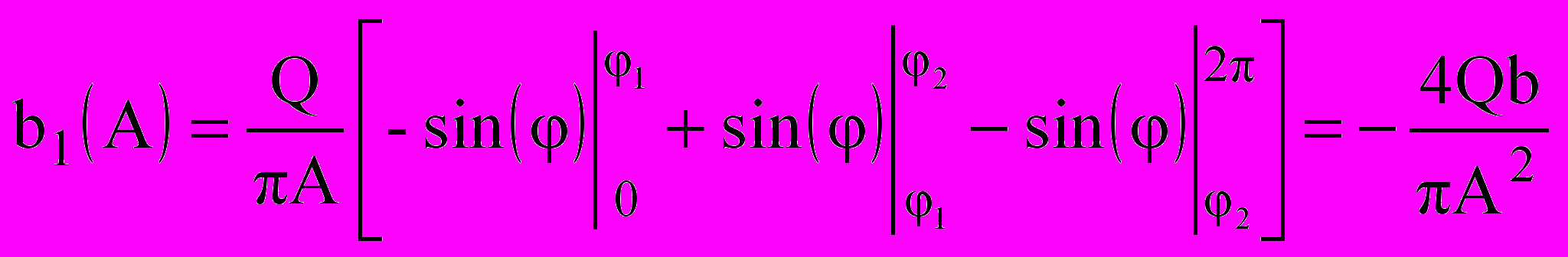, (9.19)

Для случая g(t)=0, исключая из системы (9.3), промежуточные переменные e(t), y(t), u(t), получаем

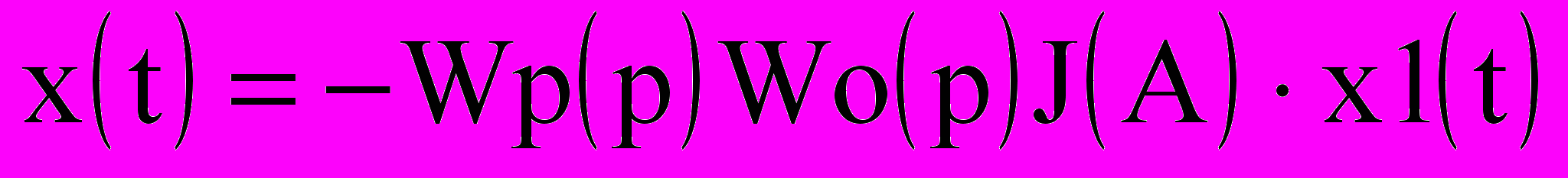. (9.20)

Условие возникновения автоколебаний (9.2) с учетом выражения (9.20) можно записать в следующем виде:

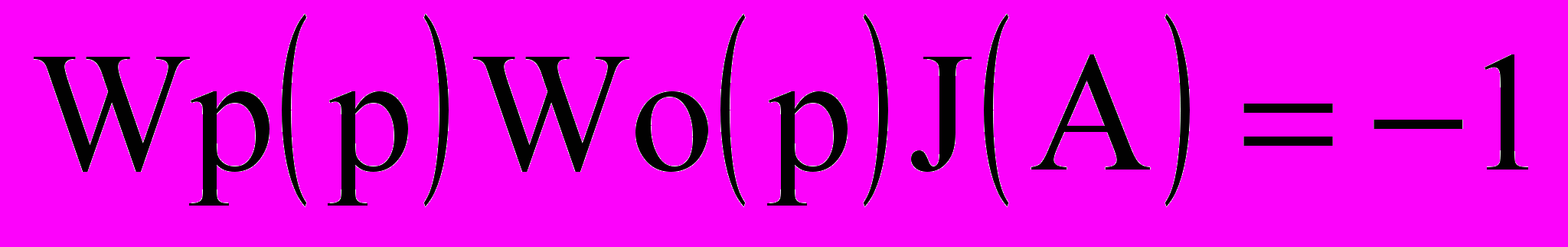. (9.21)

Для линейной части системы управления с конечной импульсной характеристикой правомерна замена р на j, т.е.

. (9.22)

Если можно найти действительные значения А и , удовлетворяющие условию (9.22) (действительные корни уравнения (9.22)), то эти значения и будут параметрами автоколебаний, возникающих в замкнутой нелинейной системе. Решать уравнение (9.22) можно графическим методом путем построения графиков функций F(j ) =Wp(j ).Wo(j) и G(A)=-1/J(A) = -1/[a(A) + jb(A)] с нахождением значений A, соответствующих точкам их пересечения. Можно также построить графики функций

H(j ) = -1/[ Wp(j ).Wo(j)] , J(A) и искать координаты их точек пересечения. В первом случае решается уравнение (9.22), преобразованное к виду: Wp(j ).Wo(j) = - 1/ J(A) , во втором - к виду: J(A)=-1/[ Wp(j ).Wo(j)].

Первый вариант построения позволяет оценить устойчивость автоколебаний по критерию Л. С. Гольдфарба: для устойчивой разомкнутой линейной системы точка пересечения комплексной частотной характеристики линейной части системы и - 1/ J(A) определяет и А, соответствующие устойчивым автоколебаниям если при увеличении А кривая - 1/ J(A) выходит за пределы контура АФЧХ или контура, дополненного окружностью с радиусом больше единицы, начинающейся на действительной полуоси (см. критерий Найквиста).