Исследование переходных процессов в замкнутых нелинейных системах управления 111

Вид материала

Исследование

Содержание Пример выполнения

Подобный материал:

• Вторая Международная научная конференция моделирование нелинейных процессов и систем, 145.53kb.
• Лабораторная работа №1 2 исследование переходных процессов, 92.12kb.
• Природа явлений в нелинейных цепях гораздо сложнее и многообразнее чем в линейных, 149.95kb.
• Расчет параметров автоколебательных процессов в нелинейных системах автоматического, 442.41kb.
• О новом поколении компьютерных лабораторных практикумов по электрофизике, 9.71kb.
• Применение среды labview для исследования переходных процессов в нелинейных цепях, 52.55kb.
• Моделирование переходных электромеханических процессов в пвк анарэс, 55.75kb.
• Переходные процессы в электрических системах рабочая программа, методические указания., 137.38kb.
• Лекция №4. Операторный метод расчета переходных процессов, 59.84kb.
• Курс: Регулярная и хаотическая динамика нелинейных систем, 278.41kb.

Пример выполнения

Запишем начальные неизменяемые условия, затем с учетом полученных аналитически функции а₁(А) и b₁(A), запишем комплексную функцию нелинейного звена и частотную характеристику линейной части:















Для поиска значений А и  введем функцию

<sub>,

представляющую собой левую часть решаемого комплексного уравнения. Зададим начальные значения неизвестным и запишем процедуру решения нелинейного уравнения:</sub>













Проверка:









Для построения графиков комплексных функций частотной характеристики линейной части системы и обратной характеристики нелинейного звена, введем функцию

_{и определим область изменения аргументов:}

, A0:=b,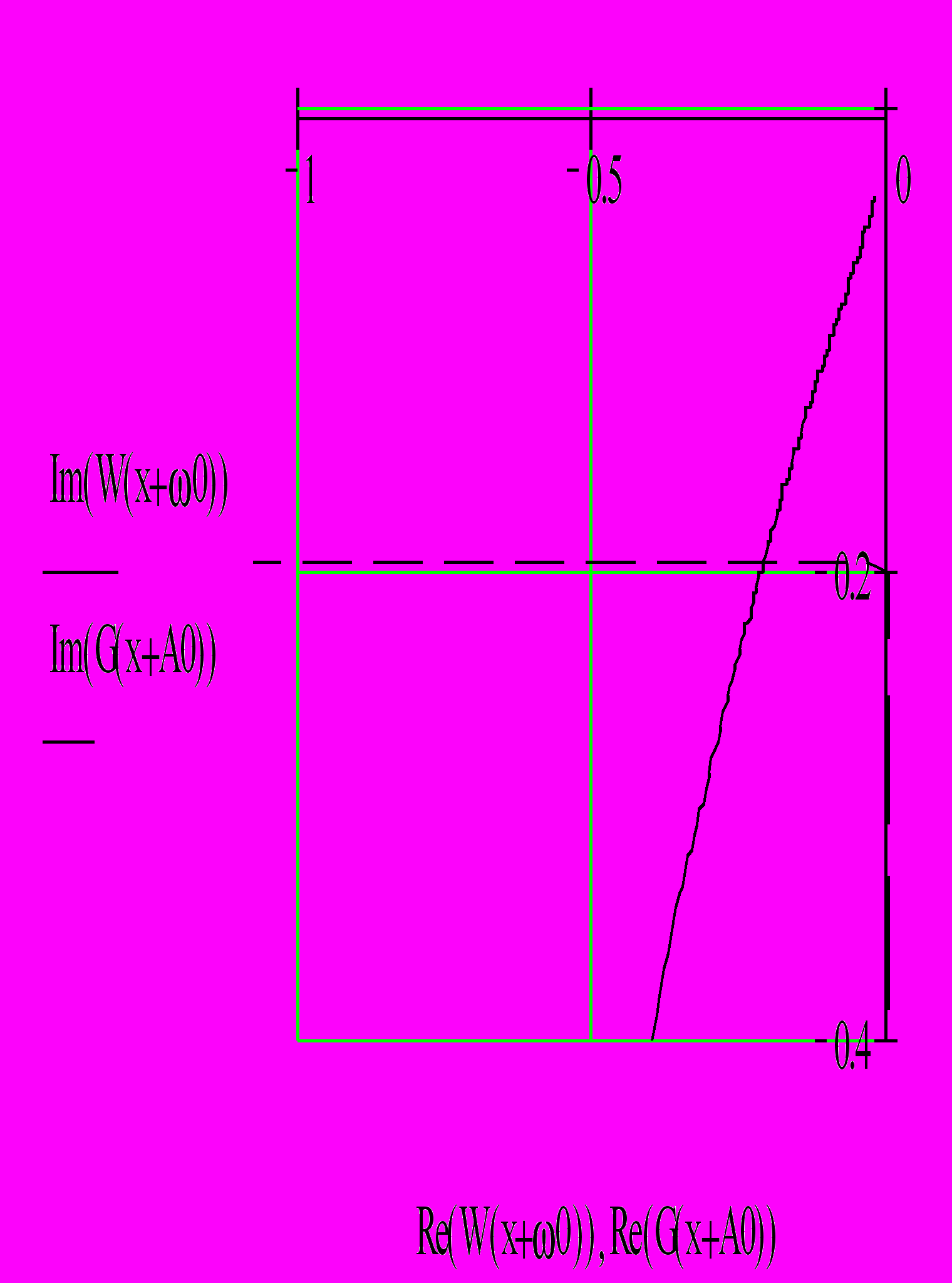



Рис. 9.3. Комплексные функции

Значения А и  в точке пересечения графиков являются решением уравнения (9.22). Поскольку в этой точке функция G(A) выходит из области АФЧХ линейной части, возникающие автоколебания, в соответствии с критерием Гольдфарба, будут устойчивыми.

Проверка по переходному процессу:







З
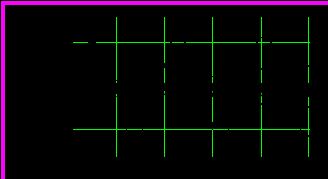
апишем программу из лабораторной работы 8 и построим графики переходных процессов без сигнала u.

Рис.9.4. Переходные процессы

Ф
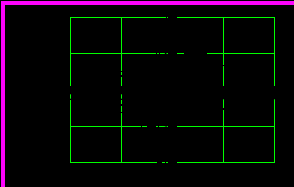
азовая траектория для указанных выше начальных условий имеет вид:

Рис.9.5. Фазовая траектория

Значения амплитуды сигнала х и периода колебаний, полученные из графиков рис.9.4, примерно равны 0,7 и 3,9, что достаточно близко к рассчитанным выше.

Фазовая траектория показывает, что в системе возникают устойчивые автоколебания с мягким возбуждением колебаний.