Исследование переходных процессов в замкнутых нелинейных системах управления 111

Вид материала

Исследование

Содержание Контрольные вопросы Содержание отчета Лабораторная работа n11 исследование качества регулирования в замкнутых линейных системах при случайных воздействиях Порядок выполнения работы Теоретические сведения

Подобный материал:

• Вторая Международная научная конференция моделирование нелинейных процессов и систем, 145.53kb.
• Лабораторная работа №1 2 исследование переходных процессов, 92.12kb.
• Природа явлений в нелинейных цепях гораздо сложнее и многообразнее чем в линейных, 149.95kb.
• Расчет параметров автоколебательных процессов в нелинейных системах автоматического, 442.41kb.
• О новом поколении компьютерных лабораторных практикумов по электрофизике, 9.71kb.
• Применение среды labview для исследования переходных процессов в нелинейных цепях, 52.55kb.
• Моделирование переходных электромеханических процессов в пвк анарэс, 55.75kb.
• Переходные процессы в электрических системах рабочая программа, методические указания., 137.38kb.
• Лекция №4. Операторный метод расчета переходных процессов, 59.84kb.
• Курс: Регулярная и хаотическая динамика нелинейных систем, 278.41kb.

Контрольные вопросы

1. На чем основан метод гармонического баланса, метод гармонической линеаризации?

2. Как описать зависимость между входной гармонической и выходной функциями нелинейного звена с помощью ряда Фурье?

3. Как записать условие возникновения автоколебаний в замкнутой нелинейной системе?

4. Как оценить устойчивость автоколебаний, возникающих в замкнутой нелинейной системе?

Содержание отчета

Отчет должен содержать:

1. Титульный лист, название и цель работы, постановку задачи в соответствии с вариантом задания.
   
2. Структурную схему исследуемой системы.
   
3. Передаточные функции исследуемого объекта, регулятора, характеристику нелинейного звена.
   
4. Уравнения, описывающие сигналы в системе, графики переходных процессов, значения частоты колебаний и амплитуды х1.
   
5. Комплексную характеристику нелинейного звена.
   
6. Рассчитанные значения частоты колебаний и амплитуды х.
   
7. Выводы о соответствии между расчетными параметрами колебательных процессов и результатами моделирования, об устойчивости колебательных процессов.
   

Задание

Выполнение настоящей работы производится по данным лабораторной работы №9.

ЛАБОРАТОРНАЯ РАБОТА N11 ИССЛЕДОВАНИЕ КАЧЕСТВА РЕГУЛИРОВАНИЯ В ЗАМКНУТЫХ ЛИНЕЙНЫХ СИСТЕМАХ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

Цели работы: закрепление теоретических сведений по динамике замкнутых систем управления, приобретение навыков расчета параметров случайных процессов на выходе линейной системы управления, а также ошибки в системе регулирования.

Порядок выполнения работы

Провести исследование влияния входного случайного процесса и параметров регулятора для замкнутых линейных систем регулирования на дисперсию и математическое ожидание ошибки регулирования при нулевом и ненулевом входном воздействии:



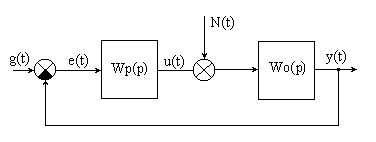
Рис. 10.1. Структурная схема системы регулирования

• установить нулевой уровень входного сигнала g(t), и, задав параметры случайного процесса, с помощью генератора случайных процессов сформировать реализацию процесса N(t) в виде массива случайных значений;
  
• рассчитать корреляционную функцию и спектральную плотность для ограниченной реализации случайного процесса используя дискретные формулы свертки и преобразования Фурье;
  
• промоделировать прохождение случайного процесса через апериодическое звено первого или второго порядка путем решения соответствующего конечно-разностного уравнения со случайным процессом в правой части;
  
• рассчитать корреляционную функцию и спектральную плотность для реализации случайного процесса на выходе линейного звена, полученной на предыдущем этапе;
  
• определить ту же спектральную плотность путем перемножения спектральной плотности процесса на входе линейного звена на квадрат амплитудно-частотной характеристики звена; сравнить со спектральной плотностью полученной в предыдущем пункте;
  
• задать коэффициенты передачи регулятора, удовлетворяющие требованиям устойчивости системы;
  
• промоделировать прохождение случайного процесса через систему и получить оценки математического ожидания и дисперсии ошибки регулирования е(t);
  
• изменив коэффициенты передачи регулятора с сохранением устойчивости системы, вновь получить оценки математического ожидания и дисперсии ошибки;
  
• повторить моделирование при ненулевом входном воздействии;
  
• все результаты занести в таблицу (табл.10.1);
  

Таблица 10.1

Параметры системы и случайных процессов

N

g

Kn

Ki

Kd

m вх

D вх

m е

D e

• для исходного случайного процесса типа «белый шум» с корреляционной функцией
  

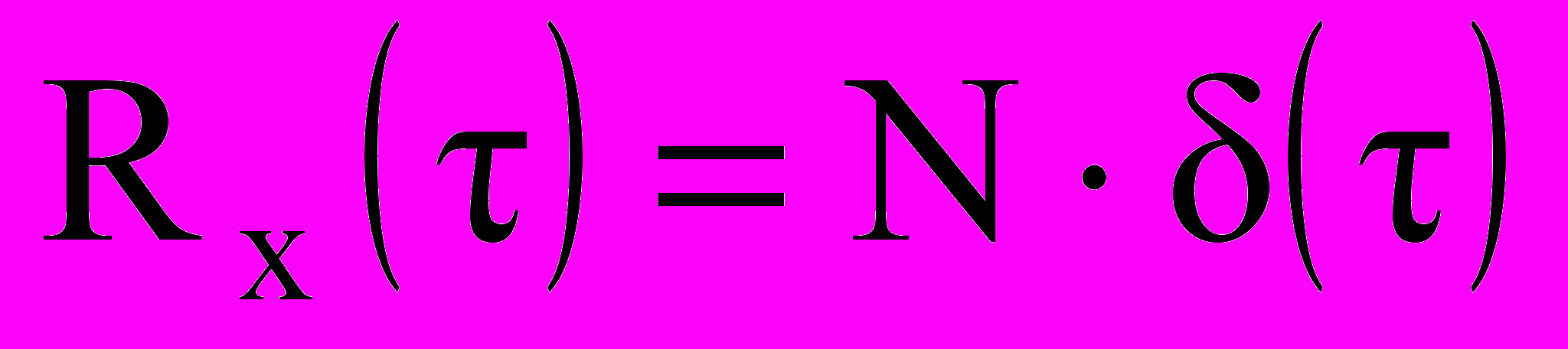(10.1)

вывести выражение корреляционной функции фильтрованного процесса на выходе линейного звена и записать выражение для спектральной плотности;

• записать выражения для математического ожидания и дисперсии ошибки регулирования, рассчитать математическое ожидание и дисперсию ошибки аналитически;
  
• провести анализ влияния параметров случайных процессов и коэффициентов передачи регулятора на величину ошибки, проверить выводы по результатам моделирования.
  

Теоретические сведения

Случайной функцией называется функция, принимающая случайную величину при каждом значении аргумента. Случайную функцию, аргументом которой является время t, называют случайным или стохастическим процессом. Для описания случайных процессов используются многомерные функции распределения вероятности и плотности распределения вероятности, математическое ожидание и дисперсия, корреляционные функции и спектральные плотности. Случайный процесс с постоянным математическим ожиданием называют стационарным, с нулевым математическим ожиданием – центрированным. Стационарные случайные процессы, результаты усреднения которых по времени и по множеству совпадают, называют эргодическими. Случайный процесс с бесконечно малой шириной корреляционной функции носит название “белого” шума и обозначается, зачастую, как N(t). Спектральная плотность такого процесса постоянна по всей частоте.

Корреляционная функция эргодического процесса x(t), характеризующая взаимозависимость значений случайного процесса во времени (изменчивость во времени), определяется как

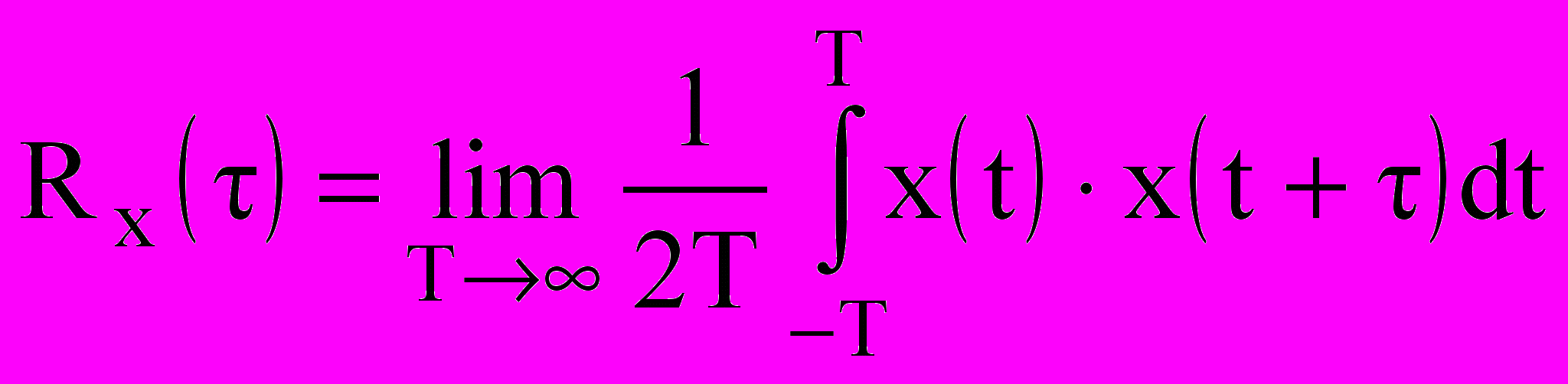. (10.2)

Для ограниченной реализации случайного процесса, полученной измерением его величины через равные промежутки времени t (период дискретизации) на интервале времени [0,2T], приближенная дискретная корреляционная функция может быть вычислена в соответствии с выражением

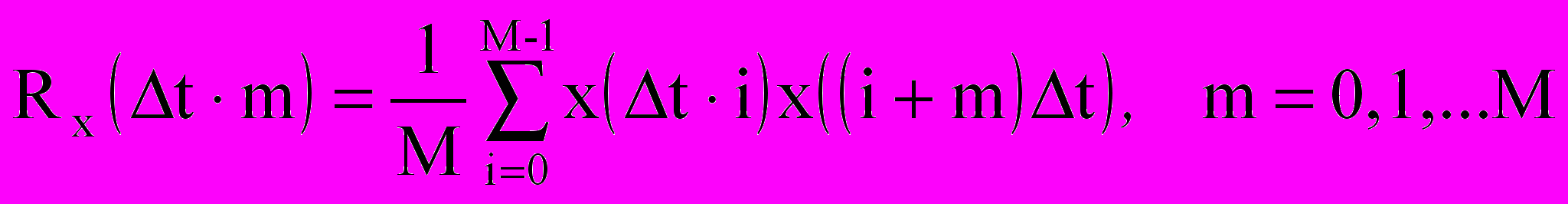, (10.3)

или как функция дискретного аргумента

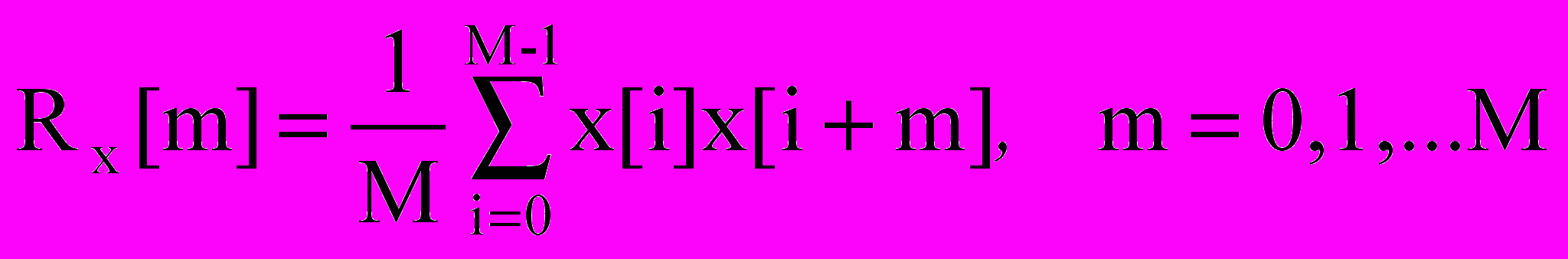, (10.4)

где M=T/t.

При увеличении Т приближенная корреляционная функция стремится к теоретической.

Значение корреляционной функции при =0 называется средним квадратом случайного процесса и равно сумме дисперсии и квадрата математического ожидания:

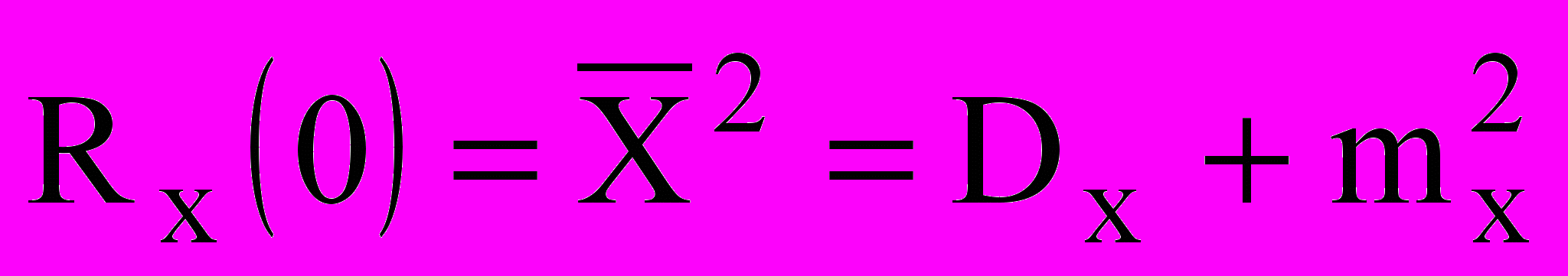. (10.5)

Спектральная плотность случайного процесса описывает распределение мощности случайного процесса по частоте и определяется преобразованием Фурье от корреляционной функции

, (10.6)

или

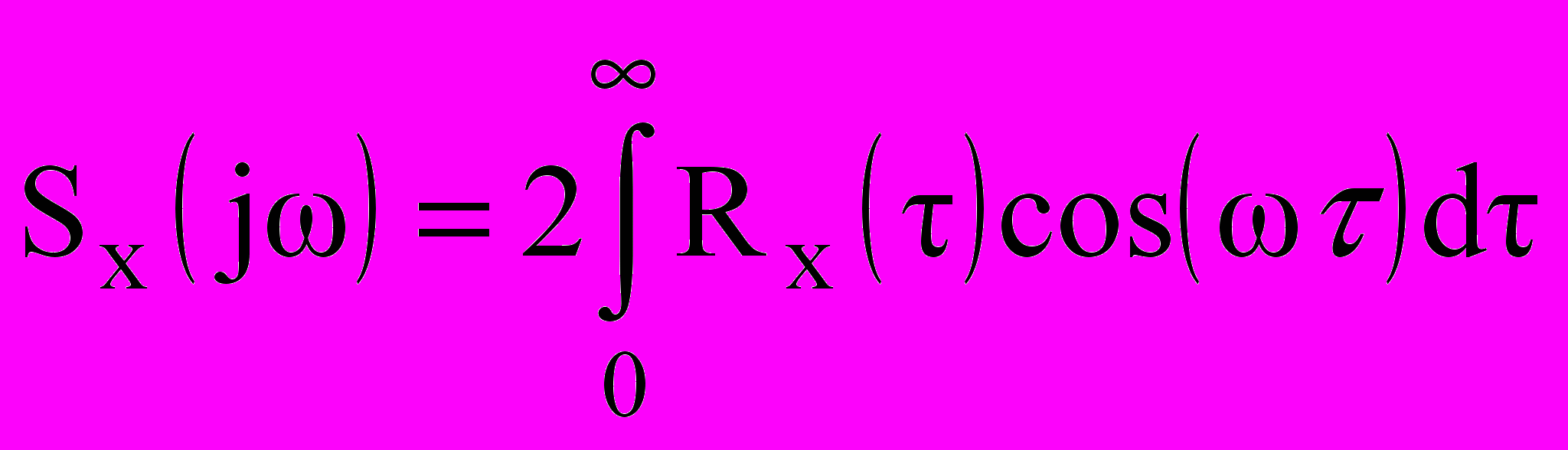. (10.7)

Для ограниченной дискретной корреляционной функции выборочная спектральная плотность определяется дискретным преобразованием Фурье

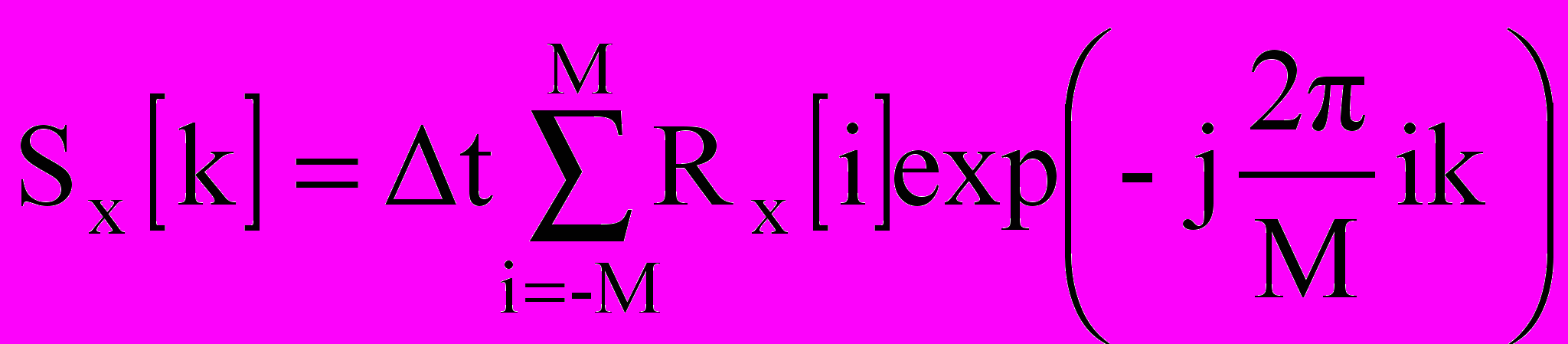, k= -M/2,...0, 1,...+M/2. (10.8)

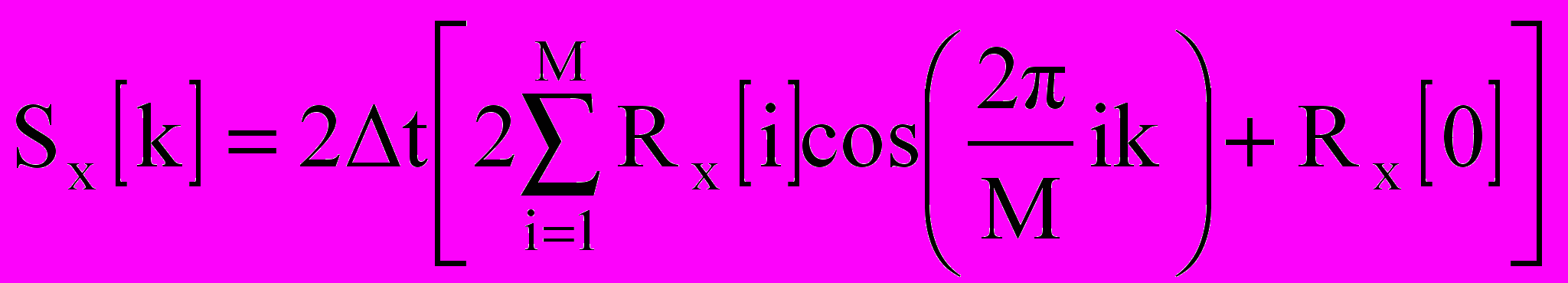, k=0,1,...M/2. (10.9)

Преобразование в форме (10.9) с удвоенной мощностью снижает объем вычислений в операциях со спектральной плотностью, так как используются только положительные частоты.

Обратное преобразование Фурье от спектральной плотности, определяющее корреляционную функцию

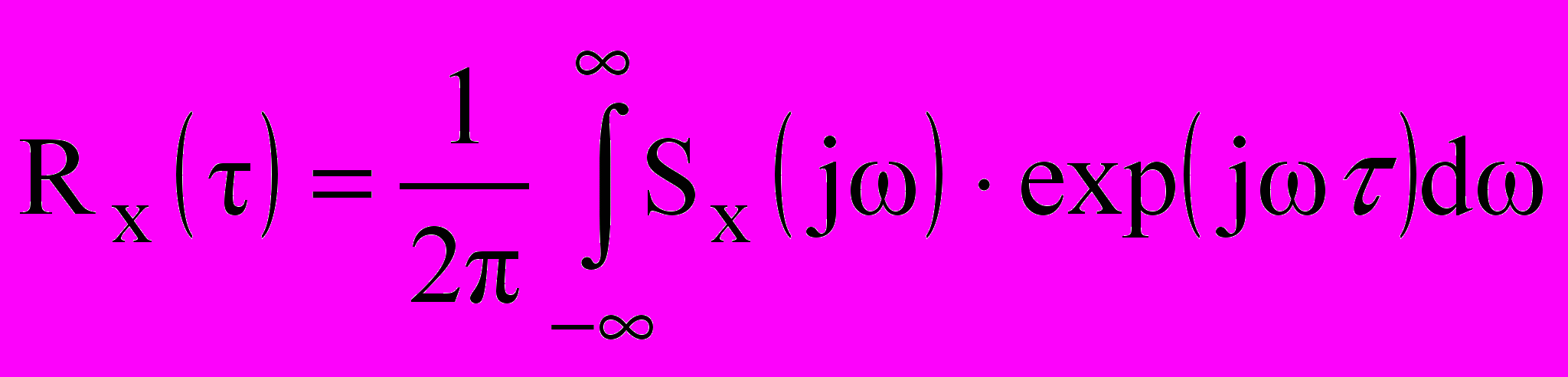, (10.10)

позволяет выразить средний квадрат случайного процесса через спектральную плотность

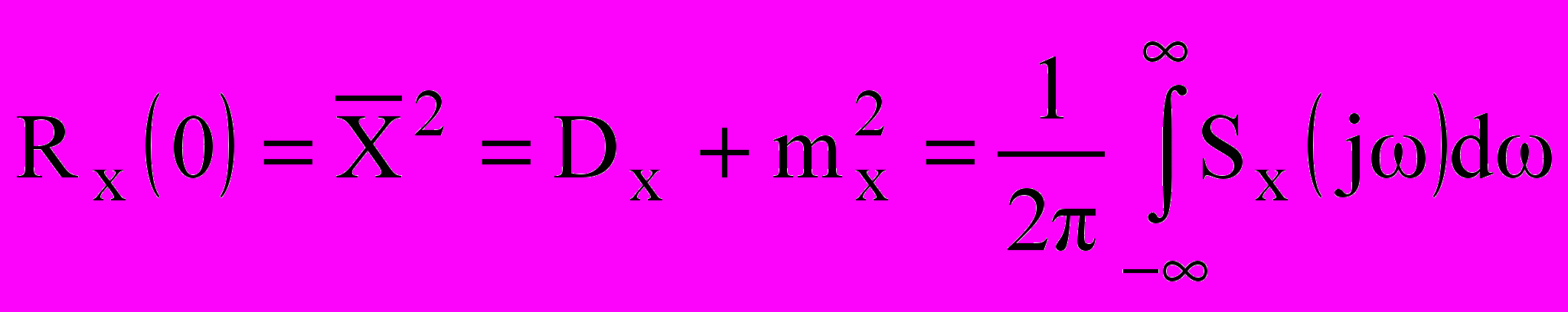. (10.11)

При прохождении через линейную систему стационарного случайного процесса x(t) с математическим ожиданием m_x , дисперсией D_x и корреляционной функцией R_x(параметры случайного процесса изменяются, но он остается случайным, достигая стационарного состояния после окончания переходного процесса. Корреляционная функция процесса на выходе линейного звена определяется как

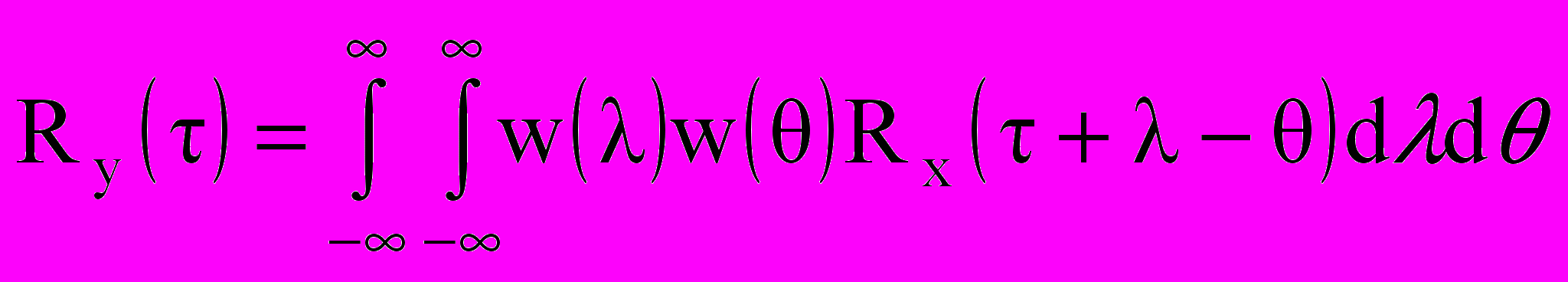, (10.12)

где 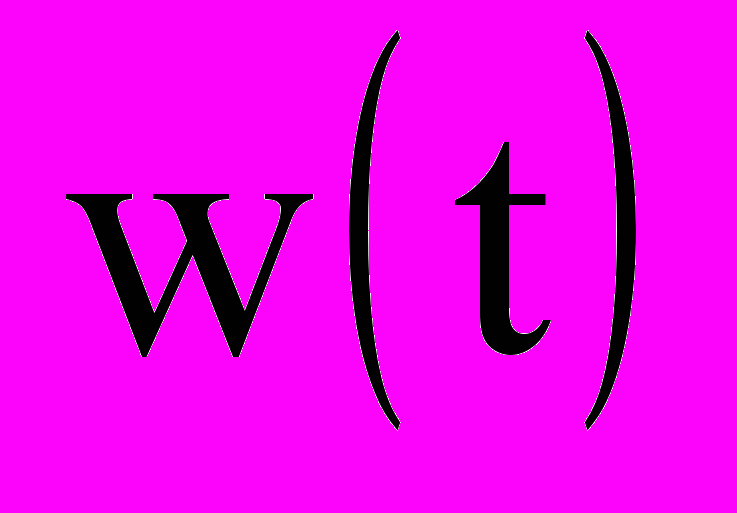- весовая функция линейного звена, записанная с учетом равенства ее нулю при t<0.

Спектральная плотность процесса y(t) на выходе линейного звена равна спектральной плотности входного процесса, умноженной на квадрат модуля частотной характеристики звена:

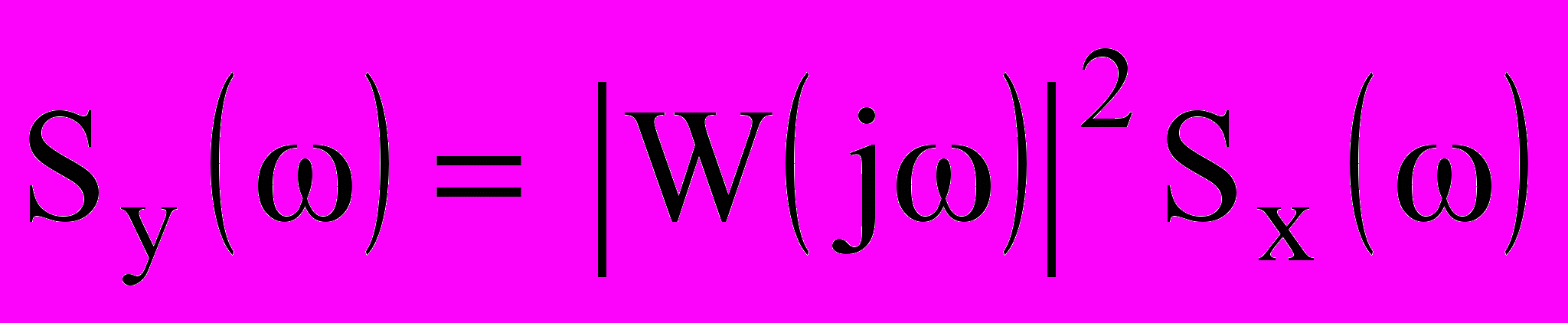. (10.13)

Сигналы на входе и выходе системы можно представить в виде сумм центрированных случайных процессов и постоянных значений, равных математическим ожиданиям, т.е.

x(t)= x^о(t)+ m_x и y(t)= y^о(t)+ m_y.

Математическое ожидание процесса m_y на выходе системы в соответствии с правилом предельного перехода между функцией и ее изображением по Лапласу [5] будет равно

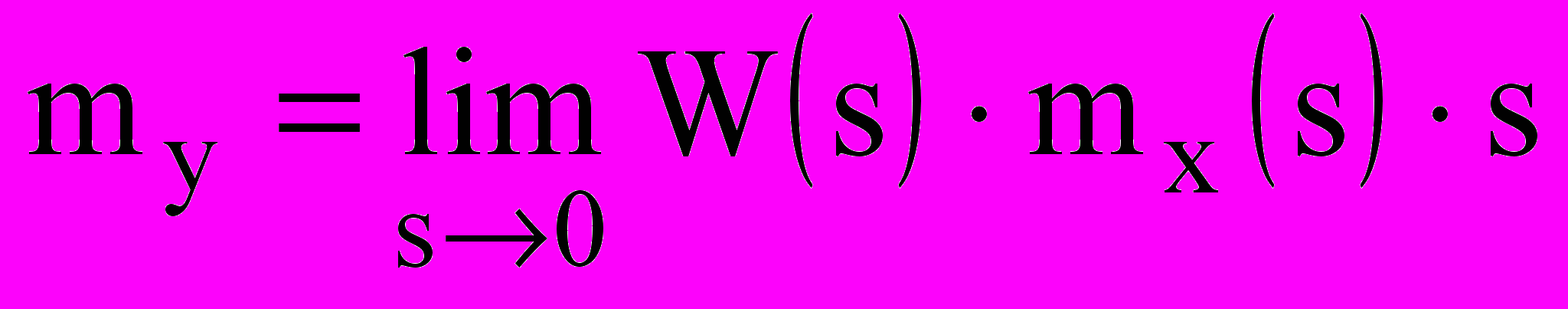или 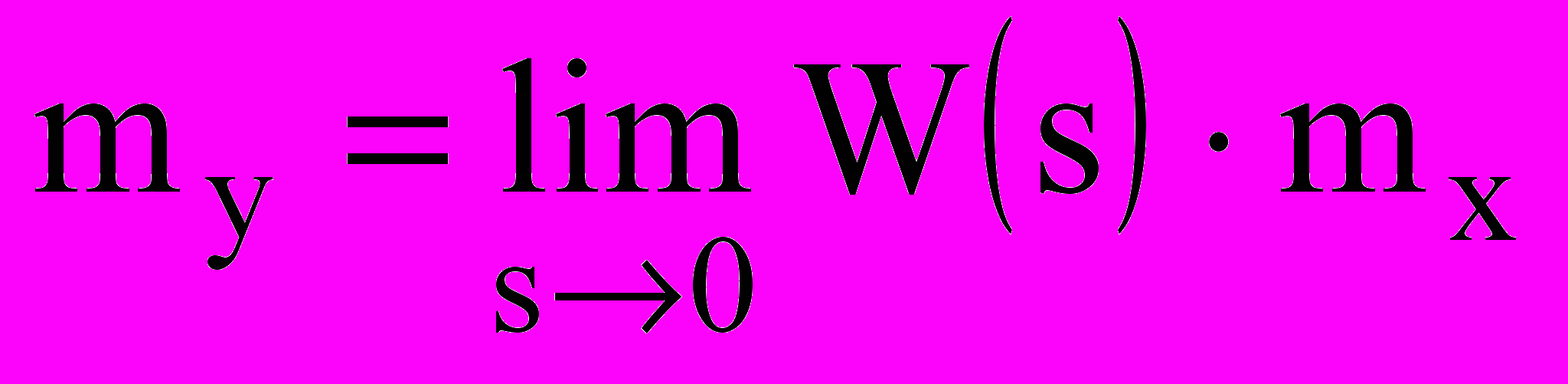(10.14)

так как m_x(s)= m_x/s.

Корреляционная функция центрированного случайного процесса y⁰(t) на выходе системы

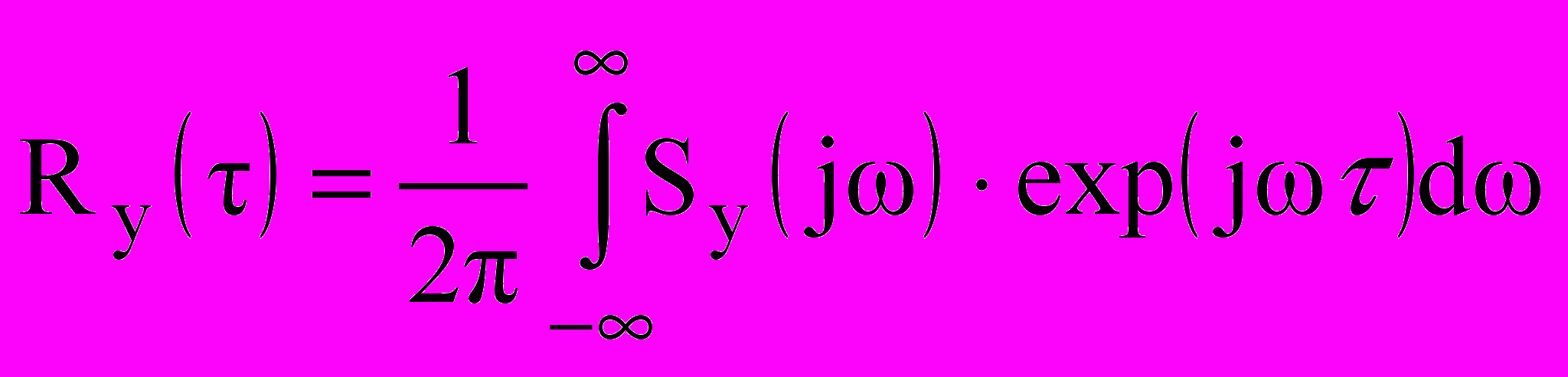, (10.15)

где S_y(спектральная плотность процесса y⁰(t), равная (10.13), аS_x( спектральная плотность центрированного случайного процесса x^о(t) на входе системы.

Дисперсия процесса y(t) может быть получена из выражения (10.12) вычитанием m_y.

В случае если оцениваются параметры ошибки, в качестве передаточной функции системы следует брать передаточную функцию от входа случайного процесса к ошибке е(t).

Если система имеет несколько входов со случайными воздействиями, то, преобразуя ее структурную схему, их можно свести к одному. Структурная схема, представленная на рис.10.1, после преобразования примет вид:



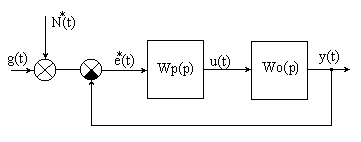
Рис.10.2. Преобразованная эквивалентная схема

Случайный процесс N*(t) формируется при прохождении N (t) через линейное звено с передаточной функцией 1/W_р(jа e*(t) равна g(t)-y(t)+ N*(t).

В соответствии с преобразованной схемой, входной процесс системы при постоянном входном воздействии g(t)=g₀ , можно представить как сумму постоянного сигнала, равного g₀+m_N* , и центрированного случайного процесса N*⁰(t). Ошибка регулирования определяется также, как и в исходной схеме рис.10.2, т.е.

e(t)=g₀-y(t),

а случайный процесс на выходе системы равен

y(t) = W_з(p)[g₀(t)+N*(t)].

Если воздействующие на систему случайные процессы g(t) и N(t) коррелированы между собой, то спектральная плотность на выходе системы определяется как

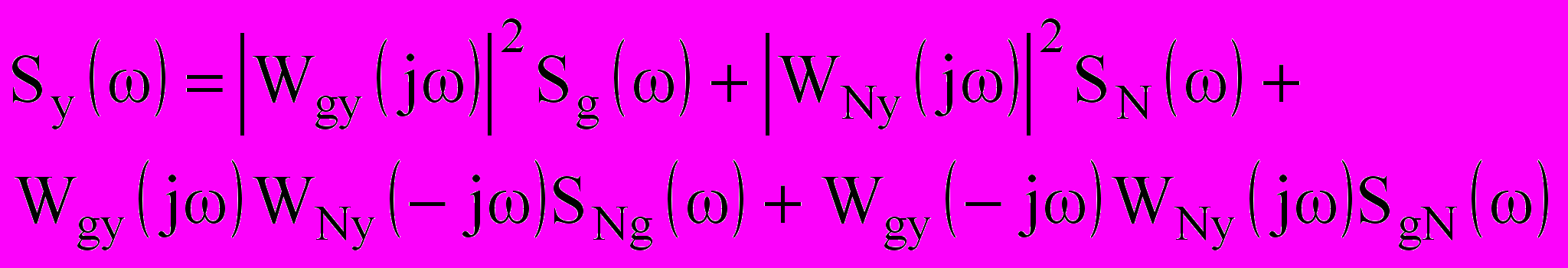, (10.15)

где S_Ng() и S_gN() – взаимные спектральные плотности процессов g(t) и N(t).