Geum.ru

Исследование переходных процессов в замкнутых нелинейных системах управления 111

Вид материалаИсследование

Содержание


Пример моделирования случайных процессов в линейных системах
Контрольные вопросы
Содержание отчета
Подобный материал:
1   2   3   4   5   6

Пример моделирования случайных процессов в линейных системах


1. Генерация массива N случайного процесса N(t) для нормального закона распределения вероятности случайных величин с математическим ожиданием mN и среднеквадратическим отклонением N. Размер массива - М2 значений.


M:=2000 M2:=2M+1 T:=200 mN:=0 N:=2 N0:=0








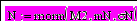
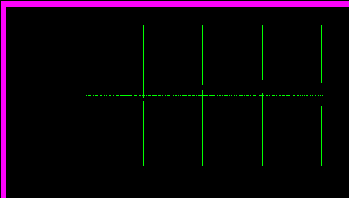
Рис. 10.3.Фрагмент реализации случайного процесса

2. Вычисление корреляционной функции RN(t).

Процедура вычисления:




Обращение к процедуре

.



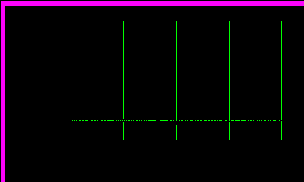
Рис. 10.4. Корреляционная функция случайного процесса

Средний квадрат случайного процесса R0=4.294


3. Вычисление спектральной плотности:

.

Средний квадрат случайного процесса для дискретной спектральной плотности определяется как:

, DN=4.311.

Результат вычислений должен быть достаточно близок к полученному ранее R0 .



Рис. 10.5. Участок дискретной спектральной плотности

4. Прохождение случайного процесса через линейное звено, выполняющего фильтрацию исходного случайного процесса типа «белый» шум, моделируется путем решения описывающего звено конечно-разностного уравнения, в правую часть которого подставляются значения исходного случайного процесса. Параметры звена и конечно-разностное уравнение для расчета сигнала на выходе звена:







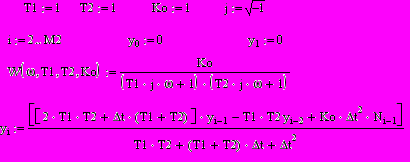
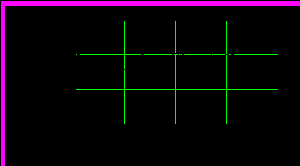
Рис.10.5. Сигнал на выходе линейного звена

Корреляционная функция сигнала на выходе звена вычисляется аналогично корреляционной функции исходного случайного процесса: .



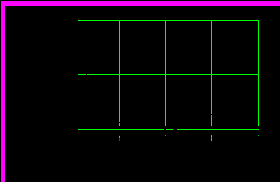
Рис. 10.6. Корреляционная функция y(t)

Средний квадрат случайного процесса y(t) равен: R0=0.082.

Спектральную плотность сигнала y(t) вычислим для контроля двумя методами: через дискретное преобразование Фурье сигнала y(t) и как произведение спектральной плотности исходного случайного процесса и квадрата АЧХ звена:










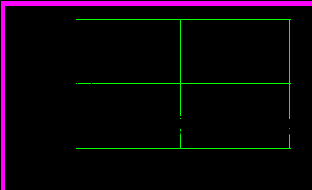
Рис. 10.7. Спектральная плотность y(t)

Средние квадраты случайного процесса y(t):

.


5. Влияние случайного процесса на ошибку регулирования рассмотрим для нулевого задания g. Для замкнутой системы (рис. 10.1) с ПИД-регулятором и реальным интегрирующим звеном в качестве объекта управления передаточная функция по каналу возмущение – выход равна:

.

Поскольку задание нулевое, ошибка регулирования противоположна по знаку выходу системы т.е. e(t)= –y(t), и передаточная функция по каналу возмущение – ошибка также равна передаточной функции возмущение-выход, взятой со знаком минус:

.

Частотную характеристику запишем по передаточной функции



Зададим параметры объекта Ko:=2 , T1:=3, упростим частотную характеристику и запишем функцию квадрата АЧХ:



Используя спектральные плотности исходного случайного процесса SNk и фильтрованного Sk , задав коэффициенты ПИД-регулятора, выведем графики квадрата АЧХ и спектральных плотностей, а также получим значения среднего квадрата ошибки (дисперсии ошибки): Ki:=1 Kn:=2 Kd:=4







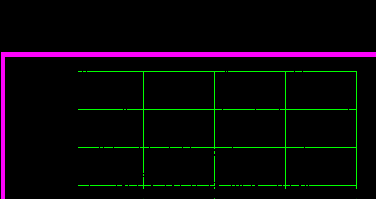
Рис.10.8.Спектральная плотность ошибки регулирования, исходного «белого» шума и квадрат АЧХ





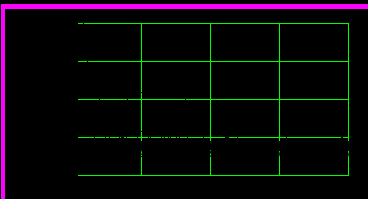
Рис.10.9.Спектральная плотность ошибки регулирования, фильтрованного случайного процесса и квадрат АЧХ

Последовательно изменяя значения коэффициентов ПИД – регулятора, проведем анализ влияния коэффициентов на область частот пропускания замкнутой системы (положение области, ее ширину) и как в зависимости от перекрытия этой области со спектральной плотностью входного процесса изменяется дисперсия ошибки регулирования.

Контрольные вопросы


1. Что такое случайный процесс?

2. Какими параметрами и функциями описывается случайный процесс?

3. Какой случайный процесс называется стационарным? Эргодическим?

4. Как определить корреляционную функцию и спектральную плотность случайного процесса, прошедшего через линейную систему?

5. Как найти математическое ожидание и дисперсию ошибки системы регулирования при случайных воздействиях?

Содержание отчета


Отчет должен содержать:
  1. Титульный лист, название и цель работы, постановку задачи в соответствии с вариантом задания
  2. Структурную схему исследуемой системы.
  3. Передаточные функции исследуемого объекта, регулятора.
  4. Уравнения, описывающие сигналы в системе.
  5. Графики случайных процессов, корреляционных функций и спектральных плотностей.
  6. Значения интегральных квадратичных ошибок (средних квадратов ошибок).
  7. Результаты анализа и сделанные выводы о влиянии коэффициентов регулятора на точность отработки входного воздействия.

Задания


Для заданной передаточной функции объекта выбрать коэффициенты в таблицах 4.1-4.3, в соответствии со своим вариантом. Параметры звена, выполняющего фильтрацию «белого» шума выбрать из таблицы 10.1, параметры входного случайного процесса – из таблицы 10.2.

Таблица 10.1

№
Кф
Т1
Т2
№
Кф
Т1
Т2

1
1
0.5
1
13
1.5
0.8
1

2
1
0.5
2
14
3.5
1
2

3
2
1
1.5
15
1.5
1
1.5

4
2.
1
2
16
1.5
1.2
2

5
3
1.5
1.5
17
1.5
1.2
1.5

6
3.5
1.5
2
18
15
1.2
2

7
3
1.5
2.5
19
2.5
1.2
2.5

8
2.
1.5
3
20
2.5
2.4
3

9
2
2
2
21
2.5
2.4
2

10
2
2
2.5
22
2.5
2.4
2.5

11
2
2
3
23
2.5
2.4
3

12
2.
2
3.5
24
2.5
2.4
3.5

Таблица 10.2

№
T
mN
σN
№
T
mN
σN

1
200
0
1
14
250
0
1.8

2
200
0
1.5
15
250
0
2.8

3
200
0
2
16
250
0
3.8

4
200
0
2.5
17
250
0
0.8

5
200
0
3
18
250
0
2.2

6
200
0
3.5
19
250
0
1.2

7
300
0
1
20
400
0
3.2

8
300
0
1.5
21
400
0
1.5

9
300
0
2
22
400
0
2

10
300
0
2.5
23
400
1
2.5

11
300
0
3
24
400
1
3

12
300
0
1.7
25
400
1
1.

13
300
0
2.7
26
400
1
2.