Курс: Регулярная и хаотическая динамика нелинейных систем
| Вид материала | Документы |
- Московский энергетический институт институт Радиотехники и электроники им. В. А. Котельникова, 23.6kb.
- Московский энергетический институт институт Радиотехники и электроники им. В. А. Котельникова, 28.08kb.
- Жан-пьер шанжё, ален конн материя и мышление, 6789.87kb.
- А. В. Язенин 2010 г. Программа, 58.59kb.
- Решение систем нелинейных уравнений, 119.58kb.
- Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
- Практических: 0 Лабораторных:, 21.53kb.
- Метод касательных гиперплоскостей для решения систем нелинейных алгебраических уравнений, 25.48kb.
- Вторая Международная научная конференция моделирование нелинейных процессов и систем, 145.53kb.
- Решение систем нелинейных алгебраических уравнений, 20.84kb.
Капранов М.В., к.т.н., проф., Хандурин А.В., к.т.н., ассистент; E-Mail: handurin@mail.ru
Курс: Регулярная и хаотическая динамика нелинейных систем
Раздел: Хаотическая динамика нелинейных систем
Научно-образовательный материал, который используется или может быть использован в системе повышения квалификации по направлению радиотехника для изучения курса регулярная и хаотическая динамика нелинейных систем
Аннотация
К настоящему времени в учебные программы подготовки и переподготовки радиоинженеров-исследователей помимо традиционного курса «Теория колебаний» включаются для изучения разделы новой науки о динамическом хаосе, которая активно развивается на протяжении последних двух десятилетий
Интерес к динамическому хаосу связан с тем, что это явление встречается в нелинейных системах самой различной физической природы и может найти ряд важных практических приложений. Хаотические колебания могут возникать в строго детерминированных системах, но обладают рядом свойств, делающих их похожими на случайные колебания. Образуя новый класс сложных, широкополосных сигналов, легко реализуемых в электронных схемах, они претендуют в радиотехнике на роль переносчиков информации для систем скрытной связи.
В отечественной и зарубежной литературе имеется ряд научных монографий и учебных изданий, специально посвященных динамическому хаосу. Поскольку проявления и характеристики этого феномена чрезвычайно разнообразны, объем сведений, включаемых в такие издания, весьма велик и требует большого времени для их освоения. Кроме того, за редкими исключениями большинство учебников по хаосу предполагает довольно высокий, близкий к университетскому, уровень математической подготовки читателя.
Целью данного курса является введение в один из начальных разделов динамического хаоса - изучение хаотической динамики в нелинейных системах с дискретным временем (регулярная динамика рассматривается при этом как этап, предшествующий хаосу). Математический аппарат здесь прост, фактически он сводится к теории разностных уравнений. Понимание хаоса в системах с непрерывным временем сложнее, требуется глубокое знание теории дифференциальных уравнений. В начале приводится пример анализа хаотических движений, возникающих в динамической системе Э. Лоренца. Некоторые трактовки процессов в системах с непрерывным временем опираются на простые понятия теории систем с дискретным временем.
В вводной части проводится краткий исторический обзор первых работ по теории динамического хаоса. Показывается, что следует проводить различие между «ХАОСОМ» и «СТОХАСТИКОЙ». В словаре στόχος означает «цель», а στοχασμός переводят как прицеливание, стремление к чему либо (или στοχάζομαι – целить, дрожание при прицеливании стрелы). Даются основные определения теории, такие как динамическая система, состояние динамической системы, странный аттрактор, окна периодичности, сценарии перехода к хаосу и другие. Доказывается, что для возникновения хаоса в случае систем с непрерывным временем их размерность (порядок N нелинейного дифференциального уравнения, описывающего данную систему) должна быть не ниже 3-х. Другими словами, на языке математики такие системы (3D–динамические системы) представляются потоками траекторий в фазовом пространстве, размерность которого 3 (или выше, в соответствии с порядком дифференциального уравнения). Однако в нелинейных динамических системах с дискретным временем хаотические движения могут возникать уже в случае систем 1-го порядка (1D–дискретные динамические системы). Эти движения представляют, как говорят математики, каскады дискретных отображений и описываются нелинейными разностными уравнениями порядка 1 и выше.
Первый раздел посвящен простейшим динамическим математическим моделям одномерных динамических систем с дискретным временем. Важно подчеркнуть, что наблюдатель ничего не знает о поведении динамической системы между соседними дискретными моментами времени, поскольку он регистрирует её состояние не непрерывно, а дискретно, через эквидистантные (равноотстоящие) интервалы наблюдения Т. Значит, штриховая огибающая, произвольно соединяющая на рис.1
| наблюдаемые значения xn, должна восприниматься лишь как одна из многих (бесконечно многих!) возможностей поведения системы внутри данного интервала наблюдения. Следовательно, такое «соединение» указывает нам всего лишь на факт перехода от предыдущего наблюдавшегося значения xn к последующему xn+1. |  |
| Рис. 1. Типичная реализация динамической переменной в системе с дискретным временем |
Поэтому фактически нелинейные модели динамических систем с дискретным временем бесконечно богаче своих прототипов с непрерывным временем. В разделе показывается, как сильно может различаться поведение системы с дискретным временем и её прототипа с непрерывным временем. Рассматриваются хорошо известные модели, пришедшие из биологии и экологии (рис.2-3), а также широко распространенные и иные сценарии «эволюции», например, так называемые процессы с обострением, характерные при возгорании или взрыве. Здесь начальный рост температуры или давления во времени идет быстрее, чем при экспоненциальном законе.
 | Рис.2. Решения уравнения Мальтуса для биологической популяции на фазовой плоскости (а) и во временной области (б). |
Кроме того, иногда закон приближения к насыщению может отличаться от асимптотического, если процесс достигает установившегося постоянного значения за конечный интервал времени (например, набор веса у животных в процессе их роста) или не достигает его вовсе (точнее, процесс насыщения во времени может идти медленнее, чем экспоненциальная функция).
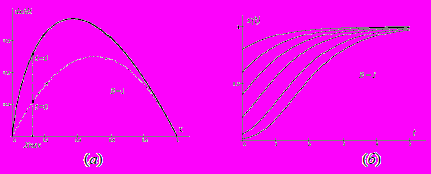 | Рис.3. Фазовый портрет (а) и графики временных решений (б) модели Гомпертца |
Во второй части курса изучается регулярная и хаотическая динамика одномерных отображений с квадратичным экстремумом. Дается определение функции последования и описывается алгоритм построения диаграмм Ламерея-Кёнигса (рис.4).
 | Рис.4. Диаграмма Ламерея – Кёнигса (а) и установление во времени 1Т-цикла (б). |
Показывается, что в теории дискретных отображений любая точка
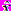 какого-либо отрезка [ха, хb], являющаяся действительным корнем уравнения
какого-либо отрезка [ха, хb], являющаяся действительным корнем уравнения 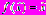 , называется простой неподвижной (или
, называется простой неподвижной (или | инвариантной) точкой преобразования. На диаграмме рис.5,а это точка пересечения графика функции последования 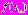 с биссектрисой с биссектрисой 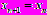 . Она является пределом последовательности . Она является пределом последовательности 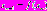 при при 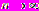 , т.е. , т.е. 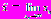 . Однако, помимо простых неподвижных точек одномерного отображения . Однако, помимо простых неподвижных точек одномерного отображения 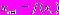 могут возникать кратные неподвижные точки, не являющиеся решениями уравнения могут возникать кратные неподвижные точки, не являющиеся решениями уравнения 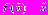 . Кратным неподвижным точкам соответствуют кратные циклы (рис.5). . Кратным неподвижным точкам соответствуют кратные циклы (рис.5). |  |
| Рис.5. Диаграмма Ламерея – Кёнигса для двукратного (2Т) цикла |
Изучается логистическое отображение, которое имеет вид параболы с квадратичным экстремумом
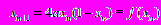 . Показывается алгоритм построения бифуркационных диаграмм при отыскании неподвижных точек уравнения при изменении «ведущего» параметра (рис.6).
. Показывается алгоритм построения бифуркационных диаграмм при отыскании неподвижных точек уравнения при изменении «ведущего» параметра (рис.6). 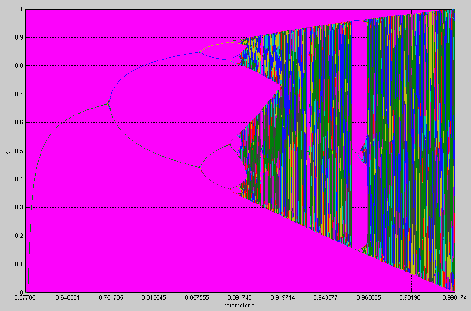 | Рис.6. Бифуркационная диаграмма логистического отображения |
Вычисляется значение скелинговых коэффициентов Фейгенбаума и значение параметра при котором лигистическое отображение формирует хаотический сигнал (рис.7). Смысл коэффициентов подобия Фейгенбаума состоит в том, что если при каждой очередной бифуркации одновременно изменять масштабы бифуркационной диаграммы по горизонтали и по вертикали, соответственно, в Fδ и Fα раз, то при достаточно большом номере N получится почти полностью самоподобная фигура. Открытие явления самоподобия (скейлинга) при бифуркациях удвоения периода явилось фактом большого теоретического значения. Оно позволяет развить аналитическую теорию для отыскания всех бифуркационных значений аN по одному лишь первому значению а1, вычислить которое не представляет труда.
 | Рис.7. Типовая реализация хаотического процесса для логистического отображения при а = 0.99 и х0 = 0.1 |
Рассмотрение рис.8 раскрывает весьма сложную картину области хаоса и обнаруживает ряд неожиданных явлений. В первую очередь это касается появления узких областей регулярных движений в зоне хаоса при а > a∞. В каждой из таких областей (их называют окнами прозрачности или окнами Шарковского – по имени советского математика А.Н.Шарковского) существуют циклы разных периодов, наиболее широкое окно соответствует циклу с периодом 3. Сильно растянутый участок бифуркационной диаграммы в области окна Шарковского с периодом 3 представлен на рис.9.
В конце второго раздела определяются численные характеристики хаотического процесса – показатели Ляпунова и информационная энтропия. Проводится обобщение динамики логистического отображения на отображение со степенным выеданием природного ресурса.
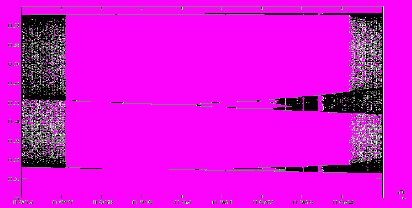 | Рис.8. Участок бифуркационной диаграммы в области регулярного режима с периодом 3 |
В третьем разделе рассмотрены процессы роста и насыщения обобщенного логистического отображения (рис.9).
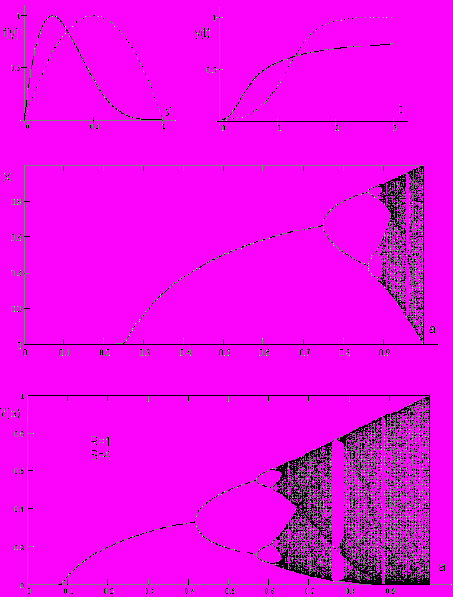 | Рис.9. Фазовые траектории и временные решения (вверху), бифуркационная диаграмма стандартного логистического уравнения (в среднем ряду) и аналогичная диаграмма обобщенного логистического уравнения (внизу) |
В четвертом разделе изучается приближенный метод ренормгруппанализа при нахождении скейлинговых закономерностей для 1-D отображений. Рассматриваются гауссовское, логистическое и трехпараметрическое (рис.10) отображения.
 | Рис.10. Набор бифуркационных диаграмм трехпараметрического отображения |
В пятом разделе изучается цифровая система фазовой синхронизации 1-го порядка с неоднородной выборкой (рис.11).
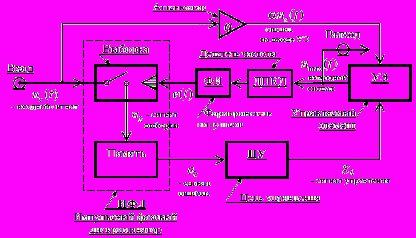 | Рис. 11. Структурная схема цифровой системы с фазовым управлением |
Эта схема содержит три основные части – импульсный фазовый дискриминатор (ИФД) типа «выборка-запоминание», управляемый элемент (УЭ) и цепь управления (ЦУ). Пример работы схемы показан на рис.12. Примером УЭ могут служить: подстраиваемый автогенератор (ПГ), синхронизированный автогенератор (САГ), усилитель высокой частоты (УВЧ) с управителем частоты (УЧ). В случае если используется ПГ, то канал входного сигнала УЭ в схеме рис. 11 необходимо исключить или установить коэффициент усиления аттенюатора α=0. При использовании САГ или УВЧ в качестве УЭ, входной канал должен присутствовать, т.е. α≠0. Роль ЦУ выполняет пассивный фильтр с операторным коэффициентом передачи Wф(p), где p≡d/dt – оператор дифференцирования. ИФД состоит из двух основных частей: схемы выборки и памяти.
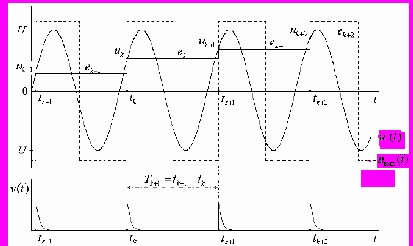 | Рис. 12. Формирование выборок uk синусоидального входного сигнала и их запомненные значения ek. |
Изучаются виды нелинейности функции отображения в зависимости от параметров и вида входного сигнала (рис.13). Располагая полученными в пятом разделе тенденциями зависимости числа неподвижных точек и характера их устойчивости от изменения ведущих параметров, приступим к точному построению диаграмм различных режимов работы систем ЦСФС на плоскости этих параметров. Такие диаграммы позволят нам легко выбирать численные значения параметров для реализации тех или иных требуемых для практики режимов ЦСФС.
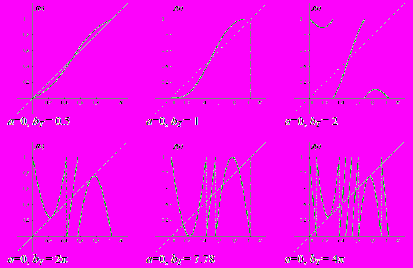 | Рис. 13. Тенденции изменения вида нелинейности f(x) стандартного отображения окружности при a = 0 и варьировании bT > 0. |
Для рассматриваемых в данном разделе ЦСФС можно произвести разбиение плоскости параметров (a,b) на области с различными видами движений (рис.14). Такой подход к исследованию широко применяется в теории нелинейных динамических систем. Он позволяет получать наглядные 2-мерные диаграммы необходимые при разработке рекомендаций по настройке системы на заданный режим работы. Эти диаграммы называют диаграммами динамических режимов, диаграммами разбиения пространства параметров или бифуркационными диаграммами (так как позволяют определять границы областей параметров, где происходят качественные изменения структуры фазового пространства, т.е. бифуркации).
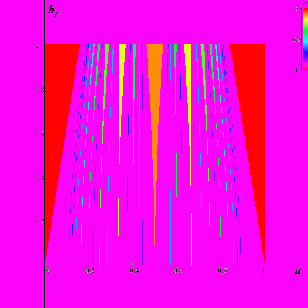

а б
Рис. 14. а) Разбиение плоскости параметров стандартного отображения окружности (a,bT) в диапазоне 0≤a≤1, 0≤bT≤1 на области с различными числами вращения W=p/q (показаны 32 зоны, соответствующие q≤10, p≤10), б) карта показателя Ляпунова стандартного отображения окружности; 0≤a≤1, 0≤bT≤10.
В шестом разделе изучаются вопросы взаимной синхронизации хаотических систем. С начала определяется сам термин «синхронизация» - он происходит от греческих слов χρονοζ (хронос - время) и συν (син – общий, соединенный), что можно перевести как «согласованное во времени поведение» взаимодействующих объектов или систем. Такое поведение возникает и проявляется как общее, фундаментальное свойство автоколебательных объектов различной природы за счет особого, нелинейного, механизма их взаимодействия, состоящего в обмене энергией автоколебаний и, в большей степени, информацией об их текущем состоянии («фазе»). Поэтому, говоря о синхронизации, часто подчеркивают, что имеют в виду именно фазовую синхронизацию, т.е. согласованное во времени изменение состояния взаимодействующих объектов. Между проявлениями эффектов синхронизации хаотических и периодических колебаний и подходами к их регистрации имеется заметная разница, поскольку естественные для периодических колебаний понятия частоты и фазы теряют четкость для хаотических. Далее выделяют особо так называемую «полную синхронизацию хаоса», или «синхронный хаотический отклик». Под этим понимается либо совпадение временных реализаций соответствующих хаотических колебаний с точностью до некоторого постоянного во времени расхождения текущих значений, либо их совпадение с точностью до постоянного сдвига по оси времени (рис.15).
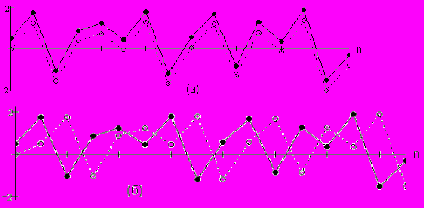 | Рис.15. Ведущее (темные точки) и ведомое (светлые точки) хаотические колебания при постоянном расхождении их текущих значений (а) и при постоянном их сдвиге во времени (б). |
Вариант синхронного отклика типа рис.15а типичен для случая энергетического взаимодействия между системами, а вариант рис.15б – при обмене информацией. Рассматриваются в качестве простых и легко анализируемых моделей двух генераторов хаоса, предназначенных для взаимной синхронизации, два однотипных отображения с квадратичным экстремумом, воздействие одной системы на другую пропорционально рассогласованию разнице их энергий
 и
и 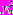 :
: 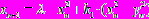 ;
; 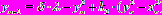 . Демонстрируются регулярные движения в системе связанных хаотических систем (рис.16).
. Демонстрируются регулярные движения в системе связанных хаотических систем (рис.16). 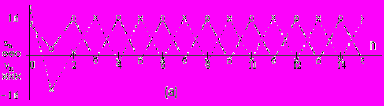 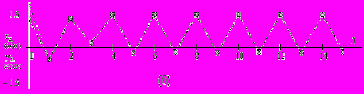 | Рис.16. Регулярные движения в взаимосвязанных хаотических системах |
Казалось бы (по опыту систем с непрерывным временем), что взаимная синхронизация двух полностью идентичных парциальных систем должна реализоваться при сколь угодно малом значении коэффициента взаимной связи k. Однако, в действительности для систем с дискретным временем картина получается совсем другой
Чтобы составить первоначальное представление о возможных типах движений во взаимосвязанной системе в случае δ = 1, на рис.17 приведены построенные с помощью MathCad бифуркационные диаграммы, показывающие, какие значения приобретают координаты xn, yn при изменении коэффициента связи k в широком диапазоне от 0 до 1.
 | Рис.17. Бифуркационные диаграмма для координаты xn (а) и координаты yn (б) при изменении коэффициента связи k. |
Один из ключевых вопросов раздела - вопрос о наступлении полной синхронизации двух систем. Количественно оценивать степень близости системы к полному синхронизму можно по-разному, мы используем для этой цели величину средней за N шагов ошибки синхронизации E(N) и её дисперсию
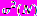 :
: 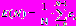 ,
, 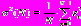 (рис.18).
(рис.18). 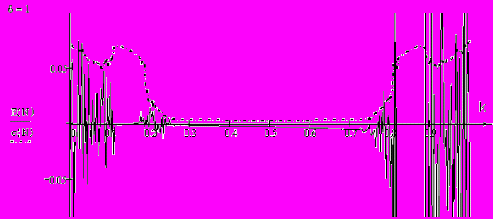 | Рис.18. Зависимость средней за реализацию длиной N =700 ошибки синхронизации и дисперсии при λ = 2, δ = 1. |
Изучение фазового портрета взаимосвязанных систем позволяет качественно оценить степень близость к полному синхронизму (рис.19). Чем белее тонким выглядит портрет, тем наиболее полная синхронизация между двумя системами. Даются способы численной оценки толщины фазовых портретов, а также предлагаются рекомендации по улучшению качества взаимной синхронизации.
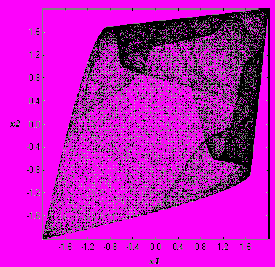
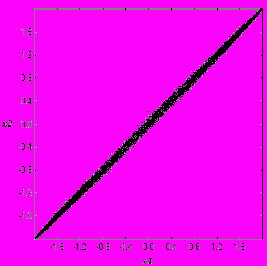
Рис.19. Фазовые портреты взаимосвязанной системы при λ =2, δ = 1 для разных значений коэффициента взаимной связи (а) синхронизация слабая; (б) синхронизация сильная
В окончании раздела рассмотрены вопросы о взаимной синхронизации сильно неидентичных систем. Видно (рис.20), что бифуркационные диаграммы в данном случае сильно видоизменяются, установить полный синхронизм практически не удается.
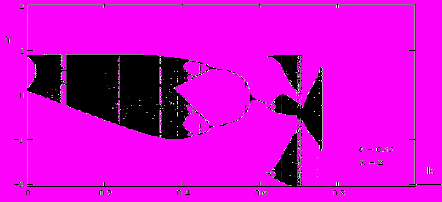 | Рис.20. Бифуркационные диаграммы, демонстрирующие разное разбиениеобластей хаоса для координаты yn. |
ЛИТЕРАТУРА
а) Основная:
1. Капранов М.В., Кулешов В.Н., Уткин Г.М. – Теория колебаний в радиотехнике. Учебное пособие для вузов. – М.: Наука, 1984. – 320 с.
2. Капранов М.В. – Регулярная и хаотическая динамика нелинейных систем с дискретным временем: учебное пособие / М.В.Капранов, А.И. Томашевский – М.: Издательский дом МЭИ, 2009. – 256 с.
3. Кузнецов С.П. – Динамический хаос (курс лекций). – М.: Физматлит, 2001. - 296 с.
4. Г. Шустер – Детерминированный хаос. Введение. – М.: Мир, 1988. – 240с.
5. Ф. Мун. – Хаотические колебания. – М.: Мир, 1990. – 312с.
6. Дмитриев А.С., Панас А.И. – Динамический хаос: новые носители информации для систем связи. – М.: Физматлит, 2002. – 252 с.
7. Динамика одномерных отображений / А.Н.Шарковский, С.Ф.Коляда, А.Г. Сивак,
В.В.Федоренко – Киев, Наукова Думка . 1989. – 216 с.
б) Дополнительная:
1. Заславский Г.М., Сагдеев Р.З. – Введение в нелинейную физику. От маятника до турбулентности и хаоса. – М.: Наука, 1988. – 368 с.
2. Анищенко В.С., Вадивасова Т.Е., Астахов В.В. – Нелинейная динамика хаотических и стохастических систем. Фундаментальные основы и избранные проблемы. / Под редакцией В.С.Анищенко. – Саратов: Изд-во Саратовского ун-та, 1999. – 368 с.
3. Малинецкий Г.Г., Потапов А.Б. – Современные проблемы нелинейной динамики. –М.: Эдиториал УРСС, 2000. – 336 с.
4. Томашевский А.И. – Компьютерная программа “Direct Maps” для исследования свойств нелинейных динамических систем с дискретным временем: учебное пособие. – М.: Издательский дом МЭИ, 2009. – 48 с.
5. Неймарк Ю.И., Качан Н.Я., Савельев В.Л. – Динамические модели теории управления. – М.: Наука, 1985. – 400 с.
6. Морозов А.Д, Драгунов Т.Н. – Визуализация и анализ инвариантных множеств динамических систем. Москва-Ижевск: Институт компьютерн. исследований, 2003. – 304 с.
7. Капранов М.В., Томашевский А.И. – Анализ фазовых траекторий в окрестностях особых точек 2–D и 3–D нелинейных динамических систем: Учебное пособие. – М.: Издательство МЭИ, 2003. – 80 с.
8. Капранов М.В. Элементы теории систем фазовой синхронизации. М.: Издательство МЭИ, 2006. − 208 с.
