Geum.ru

Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка

Вид материалаДокументы
Подобный материал:
1   ...   13   14   15   16   17   18   19   20   21

1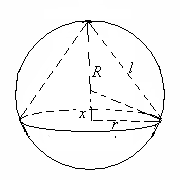1 (7 балів). В сферу радіуса вписано конус найбільшого з можливих об’єму. Визначте площу поверхні цього конуса.

Нехай – радіус кулі, – радіус основи конуса, висота конуса дорівнює . Об’єм ; , а тоді

; похідна

; . Так як при і при , то при досягає максимуму. Висота конуса дорівнює , радіус основи . Тоді площа поверхні конуса де твірна , а тоді площа

(кв.од.).


9 (7 балів). Початок координат і точка перетину прямої з осями координат визначають . Знайти точку, для якої сума відстаней до вершин цього трикутника була б найменшою.

Розв’яжемо задачу для довільного трикутника, всі кути якого менші за . Повернемо за годинниковою стрілкою навколо точки С на кут 60о, отримаємо точки та . Тоді , , тому , причому рівність можлива лише коли , , , а тому . Така точка носить назву точки Торічеллі і визначається однозначно.

У 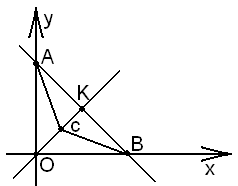нашому випадку маємо рівнобедрений прямокутний трикутник , , , , нехай – проекція точки на пряму . Відкладемо на відрізку точку так, щоб , тоді , , – точка Торічеллі для . , , . Нехай , тоді , , .

1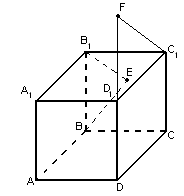1 (7 балів). Довести, що існує пряма, яка перетинає усі три прямі, на яких лежать ребра куба .

Побудуємо точки і так, щоб , тоді , адже , . Отже, - паралелограм, тобто діагоналі належить середина відрізка .


10 (7 балів). Нехай - такі точки на площині, що см, см, см, см, см. Знайти довжину .

Розглянемо : покладемо і запишемо теорему косинусів: , (кут гострий, бо ), тоді .

Розглянемо : нехай , з теореми косинусів: , (кут гострий), тоді .

Р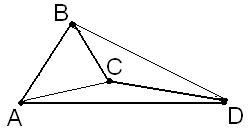озглянемо : тоді , застосуємо теорему косинусів, попередньо отримавши , (кут гострий), тоді (см) (відповідь).

Перевірка: проаналізувавши сторони усіх трикутників, робимо висновки про вигляд трикутників: - гострокутний (квадрат найбільшої сторони менший за суму квадратів двох інших сторін), - тупокутний, - гострокутний, - тупокутний. А тому перевіркою є те, що сума площ трикутників ; ; дорівнює площі . Перевірте самостійно:  (см2),  (см2),  (см2),  (см2).


9 (7 балів). Нехай - такі точки на площині, що см, см, см, см, см. Знайти довжину .

Відповідь: (см).


11 (4 бали). Нехай - такі точки на площині, що см, см, см, см, см. Знайти довжину .

Відповідь: (см).


10 (4 бали). Нехай - такі точки на площині, що см, см, см, см, см. Знайти довжину .

Відповідь: (см).


11 (4 бали). Нехай - такі точки на площині, що см, см, см, см, см. Знайти довжину .

Відповідь: (см).


11 (7 балів). Нехай - опуклий чотирикутник. З’ясувати, чи можливо, щоб , , , .

Н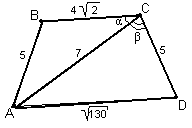ехай . Враховуючи теорему косинусів, маємо: , тоді , ; , а тоді . Врахуємо основну тригонометричну тотожність, отримаємо

А тоді . Отже, , – не є опуклим чотирикутником.


9 (7 балів). Вписано-описаним називатимемо чотирикутник, у який можна вписати коло і навколо якого можна описати коло. Довести: якщо три послідовні сторони одного вписано-описаного чотирикутника дорівнюють в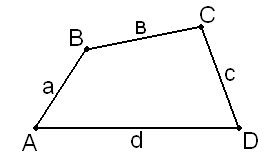ідповідно трьом послідовним сторонам іншого, то такі чотирикутники рівні.

– описаний, тому , тобто , . Нехай , тоді , адже – вписаний. За теоремою косинусів:




звідки , тепер можна знайти , тобто чотирикутник однозначно визначається за сторонами , що і доводить потрібне твердження.


10 (7 балів). Вписано-описаним називатимемо чотирикутник, у який можна вписати коло і навколо можна описати коло. Довести, якщо сторона і два прилеглі кути одного вписано – описаного чотирикутника дорівнюють відповідно стороні і двом прилеглим кутам іншого, то такі чотирикутники рівні.

Н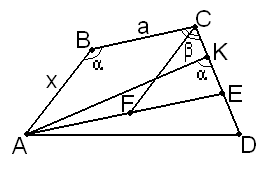ехай для певності . Через точку проведемо пряму паралельну . Нехай вона перетинає відрізок (у іншому випадку міркування аналогічні) у точці . Через точку проведемо пряму паралельну до . Нехай вона перетинає відрізок (у іншому випадку міркування аналогічні) у точці . Нехай , тоді , , . З теореми синусів для маємо: , . Оскільки ( – вписаний), , то . З теореми синусів для маємо: , . Тепер, знаючи , можна знайти . Підставивши у рівність ( – описаний) відомі значення , , , , тому отримаємо лінійне відносно рівняння (перевірте!), з якого знайшовши , можна однозначно відновити чотирикутник , що і доводить твердження задачі.