A manual for repertory grid technique
| Вид материала | Руководство |
СодержаниеИзмерение i |
- Суперкомпьютерные и grid-технологии, 242.74kb.
- Вирішення задач фінансового аналізу у Grid-середовищі завідувач кафедри ікс,, 43.42kb.
- Manual for the Design and Implementation of Recordkeeping Systems (dirks), 1279.81kb.
- Missing Instruction Manual. The Guidebook You Should Have Been Given at Birth Витейл, 2663.84kb.
- 1. ао «Казахстанская компания по управлению электрическими сетями» (Kazakhstan Electricity, 243.17kb.
- Автомобилестроение, 8.27kb.
- Отчет о работе программы в 2009 г. Институты-исполнители, 399.55kb.
- Описание требований в контексте модели прецендентов, 605.08kb.
- Руководство по эксплуатации при низких температурах Cold weather operations manual, 392.91kb.
- Промышленный маршрутизатор сотовой связи, 133.52kb.
Рис. 2. Пример оценки элемента «Келли» по восьми 11-бальным шкалам-конструктам оценочной решетки (89, 231)
сходство вовсе не означает сходства лежащих в основе этих методов теорий и предположений. Различия между репертуарной решеткой и семантическим дифференциалом огромны (см. главу 9).
Опишем один из способов заполнения оценочной решетки. Шкалы (конструкты) наносятся на чистый лист бумаги. Каждый такой лист служит для оценки одного элемента (см. рис. 2).
Таблица 10. Матрица оценок 8 элементов по 8 конструктам из книги «Теории личности» (89)
| | Фрейд | Эриксон | Мюррей | Скиннер | Олпорт | Келли | Маслоу | Роджерс |
| Свобода | 11 | 8 | 10 | 11 | 5 | 6 | 2 | 1 |
| Рациональность | 10 | 3 | 2 | 6 | 1 | 1 | 2 | 1 |
| Холизм | 3 | 1 | 3 | 11 | 3 | 3 | 1 | 1 |
| Наследственность | 3 | 10 | 6 | 11 | 6 | 9 | 5 | 4 |
| Субъективизм | 5 | 8 | 4 | 11 | 5 | 1 | 2 | 1 |
| Проективность | 4 | 3 | 4 | 11 | 1 | 6 | 1 | 1 |
| Гомеостаз | 1 | 9 | 2 | 6 | 10 | 6 | 10 | 11 |
| Познаваемость | 1 | 4 | 6 | 1 | 4 | 11 | 11 | 11 |
После того как испытуемый оценит все элементы, данные объединяются в единую матрицу (см. табл. 10).
79
Приводимая здесь решетка позаимствована из книги Хелле и Зиглера (89), посвященной анализу теорий личности. Ведущие специалисты в области психологии личности оценивались по 8 параметрам, представляющим собой теоретические допущения, лежащие, по мнению авторов книги, в основе теорий личности. Таким образом, элемент (ученый) оценивается по каждому из 8 конструктов (теоретических положений).
Такого рода матрицу вовсе не легко обработать вручную, как, скажем, матрицу ранжировок. Существует, однако, много программ машинной обработки (часть которых мы будем разбирать в главе 5). Для обработки данной матрицы мы использовали программу РА1 из статистического пакета программ для социальных наук (154). Эта программа рассчитывает корреляции между всеми парами шкальных оценок (строк), строит пространство главных компонент и размещает конструкты и элементы в этом пространстве в соответствии с их факторными нагрузками, распечатывает интеркорреляции между конструктами и другие показатели.
Графическое изображение конструктов и элементов в пространстве двух «главных компонент» приведено на рис. 3.
Хотя такое изображение и позволяет наглядно представить взаимоотношения между конструктами и элементами, тем не менее гораздо большую информа-
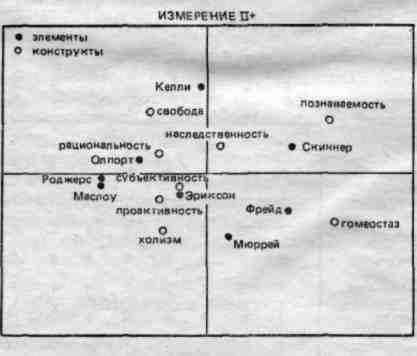
ИЗМЕРЕНИЕ I-
ИЗМЕРЕНИЕ]
ИЗМЕРЕНИЕ Ц-
Рис. 3. Размещение конструктов и элементов Таблицы 10 в пространстве двух измерений (вычисленных с помощью метода главных компонент), в соответствии с факторными нагрузками конструктов и элементов.
80
цию можно извлечь из их интеркорреляций. Это в равной степени относится и к ранговым решеткам в том случае, если проводится анализ измерений, на координатных осях которых располагаются конструкты и элементы. Интеркорреляции конструктов представлены в табл. 11, а элементов — в табл. 12.
Таблица 11
Матрица интеркорреляций конструктов, вычисленная на основании
данных табл. 10
| | | | Интеркорреляции | |и конструктов | | | |||
| | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Свобода | | | | | | | | | |
| Детерминизм | 1 | X | 0,69 | 0,58 | 0,34 | 0,69 | 0,68 | 0,82 | 0,82 |
| Рациональность/ | | | | | | | | | |
| Иррациональность | 2 | 0,69 | X | 0,40 | о,13 | 0,49 | 0,42 | 0,64 | 0,73 |
| Холизм/ | | | | | | | | | |
| Элементаризм | 3 | 0,58 | 0,40 | X | 0,54 | 0,70 | 0,90 | 0,30 | 0,56 |
| Наследственность/ | | | | | | | | | |
| Окружающая среда | 4 | 0,34 | о,Тз | 0,54 | X | 0,61 | 0,67 | 0,10 | 0.21 |
| Субъективность/ | | | | | | | | | |
| Объективность | 5 | 0,69 | 0,49 | 0,70 | 0,61 | X | 0,62 | 0,18 | 0,85 |
| Проактивность/ | | | | | | | | | |
| Реактивность | 6 | 0,68 | 0,42 | 0,90 | 0,67 | 0,62 | X | 0,46 | 0,45 |
| Гомеостаз/ | | | | | | | | | |
| Гетеростаз | 7 | 0,82 | 0,64 | 0,30 | 0,10 | 0,Т8 | 0,46 | X | 0,48 |
| Познаваемость/ | | | | | | | | | |
| Непознаваемость | 8 | 0,82 | 0,73 | 0,56 | 0,21 | 0,85 | 0,45 | 0,48 | X |
Таблица 12 Матрица интеркорреляций элементов, вычисленная на основании табл. 10
| | | | | Интеркорреляции | элементов | | | ||
| | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Фрейд | 1 | X | о.бз | 0,35 | 0,30 | 0,40 | 0,37 | 0,61 | 0,67 |
| Эриксон | 2 | 0,03 | X | 0,35 | 0,17 | 0,78 | 0,12 | 0,31 | 0,26 |
| Мюррей | з | 0,35 | 0,35 | X | 0,18 | 0,06 | 0,69 | 0,03 | 0,10 |
| Олпорт | 4 | 0,30 | 0,17 | 0,18 | X | 0,01 | 0,21 | 0,79 | 0,77 |
| Скиннер | 5 | 0,40 | 0,78 | 0,06 | 0,10 | X | 0,30 | 0,61 | 0,62 |
| Келли | 6 | 0,37 | 0,12 | 0,69 | 0.21 | 0,30 | X | 0,06 | 0.05 |
| Маслоу | 7 | 0,61 | 0,31 | 0,03 | 0,79 | 0,61 | 0,06 | X | 0,99 |
| Роджерс | 8 | 0,67 | 0,26 | 0,10 | 0,77 | 0,62 | 0,05 | 0,99 | X |
