A manual for repertory grid technique
| Вид материала | Руководство |
- Суперкомпьютерные и grid-технологии, 242.74kb.
- Вирішення задач фінансового аналізу у Grid-середовищі завідувач кафедри ікс,, 43.42kb.
- Manual for the Design and Implementation of Recordkeeping Systems (dirks), 1279.81kb.
- Missing Instruction Manual. The Guidebook You Should Have Been Given at Birth Витейл, 2663.84kb.
- 1. ао «Казахстанская компания по управлению электрическими сетями» (Kazakhstan Electricity, 243.17kb.
- Автомобилестроение, 8.27kb.
- Отчет о работе программы в 2009 г. Институты-исполнители, 399.55kb.
- Описание требований в контексте модели прецендентов, 605.08kb.
- Руководство по эксплуатации при низких температурах Cold weather operations manual, 392.91kb.
- Промышленный маршрутизатор сотовой связи, 133.52kb.
Как видно из табл. 11. Хелле и Зиглер, например, считают, что теории, делающие акцент на свободе человека в противоположность детерминизму, не имеют в своей основе допущений о «познаваемости» (—0,82) и «гомеостазе» (—0,82), однако они базируются на представлениях о «субъективности» (0,69), «рационализме» (0,69) и «активности» (0,68) («активность» в данном случае означает, что причина действия заложена в самом человеке).
81
Таблица 13. Заполненная имплнкативная
решетка
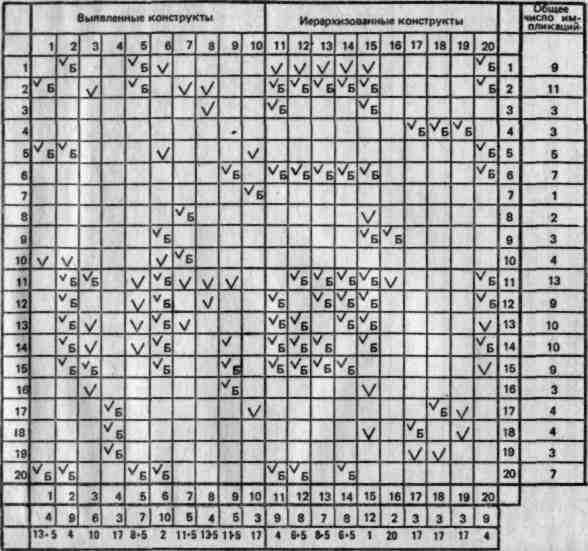
Сочувствующий - безжалостный
Внимательный к чувствам других - невнимательный
Искренний - неискренний
Ясно мыслящий - бестолковый
Откровенный - скрытный
Предубежденный- терпимый
Нервный - уравновешенный
Надежный - ненадеждныи
Умный — дурак
Уверенный в себе - неуверенный
Стремящийся понять других — центрированный
на себе Добрый — недобрый
Узнать новое о людях - чужая душа потемки Постигать вещи умом - не постигать вещи умом _Человеческое общество развивается — общество
закоснело или находится в конфликте „Честен с самим собой — обманывает себя Думать легко — думать трудно "Можно легче общаться — общаться труднее Понимают вас — думают, что вы дурак Считают себя вправе высказывать мнение
независимо от его последствий — не считают себя вправе.
Общее количество импликаций Ранг импликаций конструкта
Импликативные решетки
Импликативная решетка Хинкла
Импликативная решетка отличается от ранговой и оценочной тем, что в ней нет элементов в традиционном смысле этого слова, если не считать имплицитно присутствующего элемента «Я сам». Хинкл (88, см. также 21, 66) исследовал значение, приписываемое индивидом каждому конструкту, выраженное в терминах других конструктов. Для этого он просил испытуемого указать, «что вместе с чем происходит».
При заполнении импликативной решетки, приведенной в табл. 13, Хинкл предлагал испытуемому следующую инструкцию:
«Давайте рассмотрим этот конструкт (конструкт 1). Предположим, что вы изменились: однажды утром вы просыпаетесь и понимаете, что лучше всего вас описывает вот этот полюс конструкта, в то время как вчера лучше описывал противоположный полюс. Итак, вы осознали, что изменились в одном отношении, что еще в вас изменится (посмотрите на 19 оставшихся конструктов)? Вызовет ли изменение по этому конструкту изменения по другим конструктам? Можно ли их предсказать? Помните, что изменение по данному конструкту— это причина, в то время как изменения по другим конструктам — следствия, вызванные изменением первого конструкта. Итак, я хочу выяснить, по каким из этих конструктов можно ожидать изменений, если вы изменились по отношению к первому конструкту. Зная свое положение по отношению к данному конструкту, можете ли вы определить ваше положение по отношению к остальным конструктам?» (88, 37—38).
Каждый конструкт дважды встречается в паре с каждым другим: первый конструкт сначала выступает в паре со вторым, затем второй конструкт в паре с первым и т. д.
Подобно другим формам решеток, в импликативной решетке каждый элемент записан на отдельной карточке и обязательно пронумерован (на лицевой стороне или на обороте — неважно). Конечно, использование пронумерованных карточек не такая большая хитрость. Существует много других, может быть, лучших способов проведения эксперимента, но мы делимся с вами собственным опытом поиска удовлетворительной процедуры.
Как видно из табл. 13, испытуемый сообщил, что изменение по отношению к первому конструкту повле-
83
чет за собой изменения по отношению к конструктам 2, 5, 6, 11, 12, 13, 14, 15 и 20. Буквой «Б» в таблице обозначены реципрокные отношения: второй конструкт имплицирует пятый, а пятый имплицирует второй. Некоторые виды анализа импликативных решеток будут обсуждены ниже (после описания решеток, измеряющих сопротивление изменениям). Однако кое-какую информацию можно извлечь из решетки сразу, например сведения об общем количестве импликаций. Если решетка пестрит галочками, можно утверждать, что испытуемый использует систему, в которой доминирует один суперординатный конструкт—«это либо черное, либо белое». Если галочки почти отсутствуют, можно предположить, что системе не хватает целостности, причинных связей. Решетка, приведенная в табл. 13, в этом смысле занимает промежуточное положение. Однако «промежуточный»—это чисто «клиническая оценка», так как формальных нормативов в настоящее время не существует.
Решетка, измеряющая сопротивление изменениям
Эта решетка была разработана также Хинклом. Наряду с другими гипотезами он хотел проверить и гипотезу о том, что суперординатные конструкты в большей степени, чем субординатные, устойчивы к переменам и что сопротивление изменениям прямо связано со степенью суперординатности конструкта в импликативной решетке. По Хинклу, уровень суперординатности импликаций конструкта определяется простым подсчетом числа импликаций в каждом столбце (в импликативной решетке), а подсчет числа импликаций в каждой строке позволяет определить субординатные импликации.
Приводимая в табл. 14 решетка, измеряющая сопротивление изменениям, получена в результате сопоставления всех конструктов между собой. В данном случае такое сравнение проводилось один раз: после сравнения первого конструкта с остальными девятнадцатью он больше не использовался. Таким образом, девятнадцатый конструкт сравнивался только с двадцатым, то есть заполнялась половина матрицы. После выяснения того, на каком полюсе каждого конструкта испытуемый хотел бы видеть себя, Хинкл предлагал ему следующую инструкцию:
«Посмотрите на эти два конструкта. Галочкой отме-
84

чен тот полюс, на котором вы бы хотели поместить себя. Теперь предположим, что по отношению к одному из этих конструктов вы изменились и оказались на «нежелательном» его полюсе, а по отношению к другому конструкту ваше положение не изменилось. По какому из этих двух конструктов вы предпочли бы не изменяться? Помните, что вам придется измениться по другому конструкту. Какое из двух изменений менее желательно для вас? Хотелось бы, чтобы вы сделали выбор во всех случаях, когда это возможно. Только в двух случаях выбор невозможен. Во-первых, тогда, когда оба изменения в равной степени нежелательны. В большинстве случаев, однако, можно отыскать различия между ними и сделать выбор. Второй случай — это тот, когда логически невозможно измениться по отношению к одному конструкту и не измениться по отношению к другому. Дайте мне знать, если столкнетесь с каким-либо из этих двух случаев. Есть ли у вас вопросы?» (88, 36).
В приводимой в табл. 14 решетке, измеряющей сопротивление изменениям, крестик означает, что конструкт в столбце сопротивляется изменению; пропуск означает, что конструкт в строке сопротивляется изменению; буква «Н» означает, что независимые изменения невозможны, а буква «Э» означает, что оба изменения в равной степени нежелательны (эквивалентны).
Непосредственная обработка этой матрицы включает в себя подсчет количества всех пропусков в строках и соответствующих им крестиков в столбцах (пропуски и крестики указывают на то, что конструкт сопротивляется изменениям). Так, у первого конструкта 8 пропусков в строке, следовательно, балл сопротивляемости изменениям равен 8. У второго конструкта 14 пропусков в строке и ни одного крестика в столбце, следовательно, для него балл сопротивляемости равен 14. У третьего конструкта 10 пропусков в строке и 1 крестик в столбце, следовательно, для него балл равен 11. Все баллы сопротивляемости изменениям в табл. 14 приводятся в нижней части матрицы. Если теперь проранжи-ровать конструкты в соответствии с этими баллами, можно выявить конструкты, наиболее стойко сопротивляющиеся изменениям. В табл. 14 ранги конструктов приводятся в самой нижней строке под баллами сопротивляемости изменениям.
Используя табл. 13 и 14, можно проверить некоторые гипотезы Хинкла относительно импликативных решеток и решеток, измеряющих сопротивление изменениям. Так, данные этих таблиц подтверждают пред-
86
положение, проверявшееся в исследовании самого Хинкла: «Ранговый порядок конструктов в решетке, измеряющей сопротивление изменениям, будет положительно коррелировать с ранговым порядком конструктов импликативной решетки». В табл. 15 приводится ранговый порядок 20 конструктов: а) ранжировка по суперординатности импликаций; б) ранжировка по баллам сопротивляемости изменениям.
Таблица 15 Ранги баллов сопротивления изменениям (табл. 14) и общее число импликаций в столбцах матрицы (табл. 13)
| | | | | Конструкты | | | | | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранжирование по а) общему количеству импликаций в столбцах матрицы 13,5 | 4 | 10 | 17 | 8,5 | 2 | 11,5 | 13,5 | 11,5 | 17 |
| б) по баллам сопротивления изменениям 11,5 | 4 | 9 | 20 | 16 | 6,5 | 17 | 3 | 9 | 19 |
| п | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| а) общее количество импликаций в столбцах матрицы 4 | 6,5 | 8,5 | 6,5 | 1 | 20 | 17 | 17 | 17 | 4 |
| б) баллы сопротивления изменениям 11,5 | 1,5 | 9 | 6,5 | 5 | 14,5 | 18 | 14,5 | 13 | 1,5 |
