A manual for repertory grid technique

Вид материала

Руководство

Содержание Методы компьютерной обработки и сравнения решеток Компьютерная обработка Анализ методом главных компонент Анализ методом главных факторов Психологический журнал

Подобный материал:

• Суперкомпьютерные и grid-технологии, 242.74kb.
• Вирішення задач фінансового аналізу у Grid-середовищі завідувач кафедри ікс,, 43.42kb.
• Manual for the Design and Implementation of Recordkeeping Systems (dirks), 1279.81kb.
• Missing Instruction Manual. The Guidebook You Should Have Been Given at Birth Витейл, 2663.84kb.
• 1. ао «Казахстанская компания по управлению электрическими сетями» (Kazakhstan Electricity, 243.17kb.
• Автомобилестроение, 8.27kb.
• Отчет о работе программы в 2009 г. Институты-исполнители, 399.55kb.
• Описание требований в контексте модели прецендентов, 605.08kb.
• Руководство по эксплуатации при низких температурах Cold weather operations manual, 392.91kb.
• Промышленный маршрутизатор сотовой связи, 133.52kb.

in

которой испытуемый готов измениться по отношению к данному конструкту (см. с. 86).

(VI) Иерархизация.

Эта процедура также предложена Хинклом (см. с. 50).

(VII) Нагрузки по первому фактору, определенные
методом «главных компонент» .

Данная мера представляет собой математически обоснованный способ выявления количества и силы связей между конструктами. Так как первый фактор обычно объясняет значительную часть общей диспер­сии, предполагается, что нагрузка по этому фактору даст представление о значимости конструкта. Предпо­лагается также, что эта мера будет тесно связана с мерой, отражающей связь с наиболее значимым кон­структом (то есть III мера).

(VIII) Нагрузка по всем компонентам, выделенным
методом «главных компонент».

Эта мера сходна с предыдущей. Для каждого конструкта подсчитываются нагрузки по всем значи­мым компонентам. Предполагается, что данный показа­тель отражает относительную значимость каждого кон­структа.

(IX) Неравномерное распределение элементов по
полюсам конструкта (оценивалось по 6-балльной
шкале).

В предыдущей работе Баннистера и Салмон был отмечен любопытный факт: если испытуемым предо­ставить свободу в использовании конструкта, то по одним конструктам они будут распределять элементы более неравномерно, чем по другим. Баннистер и Салмон предположили, что степень неравномерности коррелирует с суперординатностью, однако вопрос о характере и знаке этой корреляции остался открытым до сих пор.

(X) Субъективная оценка значимости.
Испытуемым предлагалось высказать свое мнение о

степени суперординатности конструктов.

С этой целью у 10 испытуемых были выявлены 14 конструктов. Затем каждый испытуемый оценивал с помощью этих конструктов 20 элементов, описанных на 20 карточках,— по одному на каждой карточке. Перед испытуемым выкладывалось 7 больших карточек с

символами: « + + + », « + +», « + », « —», «—», « »,

<не подходит». Положительный полюс конструкта за­писывался на листке бумаги и помещался рядом с

См. главу 5.

112

карточкой с символом « + + +», а отрицательный по­
люс— рядом с карточкой с символом « ». Испыту­
емого просили положить карточку с названием элемен­
та на соответствующее ему место на большой карточке.
Для построенной таким образом решетки подсчитыва-
лись меры суперординатности (I, II, IX).

Испытуемые затем заполняли ранговую решетку: в ней использовались все те же 14 конструктов и 8 эле­ментов, диапазон пригодности которых оказался наибо­лее широким. Подсчитывались меры III, IV, VII и VIII.

Показатели сопротивления изменениям подсчитыва­лись по методу Хинкла (см. с. 86). Конструкты предъ­являлись испытуемому попарно. Его спрашивали, на каком из нежелательных полюсов он предпочел бы оказаться, если бы ему пришлось измениться по одно­му из конструктов.

При проведении процедуры иерархизации инструк­ция менялась: испытуемого просто спрашивали, почему он выбрал именно этот полюс. Опрос продолжался до тех пор, пока испытуемый не прекращал порождать новые конструкты. Процедура повторялась в отноше­нии каждого из 14 конструктов. Показателем иерархи­зации служило общее число дополнительных конструк­тов, выявленных таким образом. Баннистер и Салмон считают эту меру наименее валидной из применявшихся ими (см. обсуждение трудностей, имплицитно присущих процедуре иерархизации, на с. 16—17).

В табл. 18 приведены интеркорреляции 10 показате­лей суперординатности. Для 14 конструктов каждого испытуемого подсчитывались 10 показателей (или ран­гов) суперординатности, что позволило выявить корре­ляции между показателями суперординатности для каждого испытуемого индивидуально. Баннистер и Сал­мон считают самой примечательной чертой этих инди­видуальных матриц большой разброс величин и направ­лений интеркорреляций показателей. Индивидуальный разброс, безусловно, выравнивает корреляции при их усреднении. Некоторые из близких к нулю средних коэффициентов корреляции, приведенных в табл. 18, действительно отражают близкие к нулю корреляции и в индивидуальных матрицах (как, например, количество экстремальных оценок (I) и величина нагрузок по всем компонентам (VIII)). Но в других случаях дело обстоит не так. Из анализа усредненной матрицы корреляций следует, что устойчивые тенденции к положительной корреляции существуют только между (а) мерами, отражающими общее количество связей данного кон­структа с другими конструктами; (б) показателями,

из



построенными н а выявлении более или менее осознава­емых самими испытуемыми суперординатных отношений между конструктами. Таким образом, показатели супер­ординатности, полученные в результате предваритель­ной статистической обработки, коррелируют между собой, коррелируют и показатели суперординатности, полученные на основе прямого опроса испытуемых. Связующим звеном между этими двумя типами показа­телей является, по всей видимости, только «диапазон пригодности конструкта».

Комментируя описанное выше исследование, Банни-стер и Мэир (21) утверждают, что «путаница будет продолжаться до тех пор, пока разнообразные операци­ональные определения положений теории не будут логично обоснованы с точки зрения самой теории» (с. 206).

114

Артикуляция

Маклуф-Норрис, Джоунс и Норрис (148) описали показатель интеграции системы конструктов, основан­ный на корреляциях между конструктами. Конструкты, значимо коррелировавшие между собой (попарно) на уровне р<0,05, образовывали первичные кластеры. Оставшиеся конструкты классифицировались следу­ющим образом. (I) Конструкт, значимо коррелировав­ший с одним или несколькими конструктами первичного кластера, получал название «ответвляющегося». (II) Конструкт, значимо коррелировавший с одним или несколькими конструктами двух или нескольких класте­ров, получал название «связующего». (III) «Изолиро­ванным» назывался конструкт, не коррелирующий (на значимом уровне) ни с одним другим конструктом.

Исследователи сравнивали решетки, заполненные испытуемыми, страдающими обсессивным неврозом², с решетками психически здоровых испытуемых. Между ними были обнаружены существенные различия.

«Концептуальная структура психически здорового человека артикулирована. Она включает в себя по крайней мере два различных кластера, объединенных посредством связующих конструктов. Концептуальная же структура больного обсессивным неврозом не арти­кулирована— это монолит, состоящий либо из одного доминирующего кластера с вторичными образованиями, либо из сегментов, образованных несколькими не име­ющими связующих конструктов кластерами» (148, 271).

Эта мера очень интересна, однако в настоящее время еще слишком мало известно об отличиях артику­лированной системы конструктов от неартикулирован-ной. Какой будет система, если взять какой-нибудь другой уровень значимости (кроме р<0,05)? Какие конструкты кластеризуются на уровне значимости, скажем, р<0,01? Становится ли система более интегри­рованной по мере снижения уровня значимости?

¹ Здесь — степень структурированности и связности системы
конструктов.— Прим. ред.

² Обсессии (от лат. obsessio — осада, охватывание) —
разновидность навязчивых состояний, выявляющихся в переживани­
ях и действиях, не требующих для своего возникновения определен­
ных ситуаций (например, навязчивое мытье рук; страх перед числом
«3», потому что в слове «рак» три буквы; страх наступить на черту
или трещину и т. п.). Обсессии наблюдаются у многих больных,
которым свойственны обычно скрупулезность, педантизм, склонность
к формализму наряду с душевной инертностью, тревожной неуверен­
ностью в себе.—Прим. ред.

115

Интегрированность восприятия себя и других

Маклуф-Норрис и Норрис (147) исследовали также и структуру отношений между представлениями испы­туемого о себе, своем идеале и о других людях. Предложенный этими авторами показатель основывает­ся на учете расстояний между элементами, определя­емых ЭВМ по программе Слейтера INGRID для анализа главных компонент (198). Эти расстояния можно под­считать и без использования компьютера, взяв за основу интеркорреляции элементов. Их можно подсчи­тать также и при стандартном анализе главных компо­нент.

Маклуф-Норрис и Норрис размещали все элементы в системе координат, образованной двумя осями — «идеальное Я» и «актуальное Я». На рис. 4 приводится



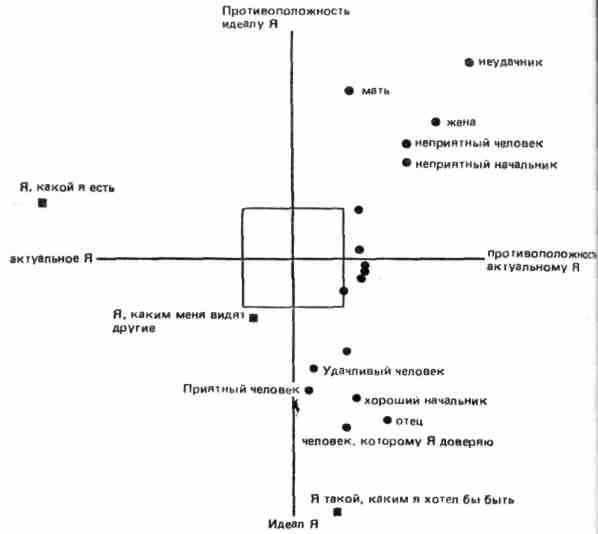
Рис. 4. Схема, на которой показаны расстояния между всеми элемен­тами в пространстве двух осей «актуальное Я» и «идеальное Я» по данным оценочной решетки, заполненной испытуемым, у которого, как видно из схемы, изолированное «актуальное Я». Обработка проводилась по программе INGRID — анализ главных компонент— Слейтера. (Рисунок взят из работы 155.)

116

размещение элементов (людей) внутри этой системы координат. «Актуальное Я» изолировано, окружающие более или менее близки к «идеальному Я», а некоторые из них далеки как от «актуального», так и от «идеально­го Я». Данный испытуемый, следовательно, знает, каким бы он хотел быть и каким бы он не хотел быть, а также чем он не является. Ему неясно только то, чем он, собственно, является в настоящее время. Авторы описывают и другие методы исследования образа «Я» с помощью решетки и способы интерпретации взаиморас­положений элементов (155). Применяя эти методы, необходимо помнить, что оси «актуальное Я» и «идеаль­ное Я» не всегда расположены ортогонально, как это изображено на рис. 4.

Конфликт

Хинкл (88) связал представление об импликативных дилеммах (с. 89) с теорией конфликтов. Двойственные отношения между конструктами наблюдаются в том случае, когда оба полюса конструкта имплицируют какой-либо полюс другого или когда оба полюса двух конструктов имплицируют друг друга.



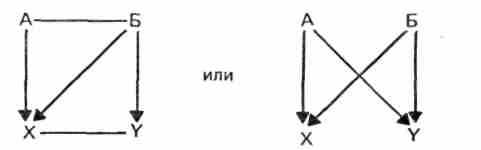
Баннистер и Мэир (21) полагают, что в импликатив-ной решетке «связи между полюсами конструктов, указываемые испытуемым (в серии разнесенных во времени парных сравнений), могут пересекаться и при­водить к противоречивым следствиям. Например, кон­структ «А+А —» может имплицировать соответству­ющие полюса конструктов «В + В —» и «С + С —». Однако впоследствии при сравнении с четвертым конструктом может выясниться, что положитель­ный полюс конструкта «С + » имплицирует отрицатель­ный полюс конструкта «Z—», тогда как «А + » имплициру­ет «Z + ». С этих позиций можно рассмотреть такие психологические понятия, как, например, «конфликт» (21, 96).

Логические несоответствия внутри решетки, измеря-

117

ющей сопротивление изменениям (см. с. 84), можно исследовать, не прибегая к помощи ЭВМ. Баннистер и Салмон (23) предложили метод подсчета показателя, названного ими «нетранзитивностью». Если испыту­емый утверждает, что в паре конструктов А и Б он скорее предпочтет измениться по конструкту Б, чем по конструкту А, а в паре конструктов Б и С он скорее предпочтет измениться по конструкту С, чем по кон­структу Б, то логично ожидать, что при сравнении конструктов А и С он предпочтет измениться по конструкту С, а не по конструкту А. Ниже приведена система подсчета, позволяющая выявить все случаи, когда X сопротивляется изменениям в большей степени, чем Y. В ее основе лежит очевидное логическое требование: если X в большей степени сопротивляется изменениям, чем Y, то X должен в большей степени сопротивляться изменениям и по всем тем конструктам, по которым Y оказывается тоже более устойчивым.

После того как испытуемый оценит все воз­можные пары конструктов и укажет для каждой пары конструкт, в большей степени сопротивля­ющийся изменениям, необходимо построить мат­рицу следующим образом. Крестик в клеточке матрицы будет означать, что испытуемый предпо­чел измениться по конструкту, расположенному по горизонтали, и не изменяться по конструкту, расположенному по вертикали. Пропуск в столбце, таким образом, указывает на конструкт, по которому испытуемый предпочел измениться, а пропуск в строке — на конструкт, по отношению к которому испытуемый предпочел не изменяться.

1. Возьмите еще один лист бумаги, приложите его к первой строке и перепишите первую строку матрицы, ставя крестики там, где в строке были пропуски, и пропуски там, где в строке были крестики. Затем в вашей копии в каждом пропу­ске напишите номера соответствующих столбцов.
   
2. Приложите эту копию последовательно ко всем строкам с номерами, соответствующими но­мерам, написанным на вашей копии (см. первый пункт).
   
3. Подсчитайте число совпадений крестиков в исследуемой вами строке и в копии. Запишите полученную цифру в соответствующую клеточку подготовленной заранее результирующей матри­цы. Полученная цифра указывает на число не­транзитивных троек для данного конструкта. Сле-
   

па

дует особо отметить, что при сравнении строк надо учитывать не только нижнюю (оставшуюся) часть матрицы, как это делается при сравнении строк обычной решетки, когда предполагается, что отношение 1 к 2 равно отношению 2 к 1. В данном случае надо всегда возвращаться и к верхней половине матрицы. Например, достигнув двенадцатой строки и сделав ее копию описанным выше способом, необходимо подняться вверх и приложить вашу копию ко всем нужным строкам и подсчитать число несовпадений: ведь каждый конструкт может входить в нетранзитивные отно­шения с другим конструктом дважды — сначала как большая посылка, а затем как меньшая посылка силлогизма.

4. Когда результирующая матрица будет пол­ностью заполнена, обработайте ее следующим образом. Подсчитайте сумму нетранзитивных тро­ек для каждого конструкта (причем не забудьте, что в результирующей матрице конструкт пред­ставлен и строкой и столбцом; возьмите общую сумму цифр во всех клеточках, соответствующих конструкту) и запишите ее в конце строки. Эта сумма представляет собой «сырой» балл нетранзи­тивности для каждого конструкта.
   
5. Умножьте число пропусков в каждой строке на число крестиков (пропустив клеточку, в кото­рой конструкт сопоставляется сам с собой). При­бавьте к полученной цифре общее число пропу­сков во всех строках, сравнивавшихся с данным конструктом. Вы получили возможное число не­транзитивных троек для каждого конструкта. Относительный балл нетранзитивности для кон­структа подсчитывается следующим образом. «Сырой» балл нетранзитивности делится на воз­можное число нетранзитивных троек и умножает­ся на 100%. Относительный балл нетранзитивно­сти для решетки в целом представляет среднее арифметическое относительных баллов нетранзи­тивности (в процентах) всех конструктов (23).
   

Слейд и Кжелдсен (197) продолжили исследования конфликтности. Их поразило сходство результатов оценки психологического конфликта (118), получаемых с помощью техники Лаутербаха и с помощью ранговой и оценочной решеток. Техника Лаутербаха, основанная на теории когнитивного баланса Хейдера (86), заключа­ется в оценке динамических отношений между тройка-

119

ми личностно значимых понятий. Эти понятия выявля­ются у пациента в ходе исследования наиболее важных для него проблем или проблем, которые заставили его обратиться за помощью к психологу (представление о себе самом всегда включается в исследование). Динами­ческие отношения между понятиями оцениваются паци­ентом по 7-балльной шкале. Они могут быть как положительными (например, нравится, помогает, усили­вает и т. д.), так и отрицательными (например, не нравится, уменьшает, мешает, ослабляет и т. п.).

Метод оценки конфликтов основан на существу­ющем в социальной психологии представлении о «несба­лансированных триадах». Триада состоит из трех поня­тий и отношений между ними. Она может быть «сбалан­сированной» или «несбалансированной». Пример несба­лансированной триады, приводимый Лаутербахом (119), можно представить в виде диаграммы:



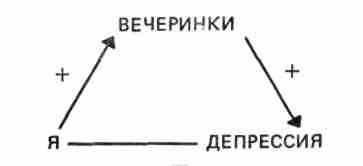
Эти отношения можно выразить так: (1) «Я люблю ходить на вечеринки», (2) «Вечеринки усиливают мою депрессию» и (3) «Я не люблю находиться в состоянии депрессии». Сбалансированной считается такая триада, в которой все отношения имеют положительный знак (то есть « + », « + », « + ») или одно отношение имеет положительный знак, а два — отрицательный (то есть « + », « —», « —»). Несбалансированной считается такая триада, в которой все отношения имеют отрицательный знак (то есть « —», « —», « —») или два отношения имеют положительный знак, а одно — отрицательный (то есть « + », « + », « —»). Лаутербах разработал программу для компьютера, вычисляющую общий балл сбалансирован­ности, общий балл несбалансированности и процентный показатель конфликтности в целом для данной процеду­ры (117).

Слейд и Кжелдсен написали программу для оценки процентного отношения несбалансированных триад кон­структов к сбалансированным, основанную на анализе интеркорреляций между конструктами. В настоящее время эти авторы изучают возможности практического

120

использования методов выявления конфликта посред­ством решеток. В одном из своих исследований они предлагали двум психологам заполнить решетку, в качестве элементов которой использовались имена те­оретиков в области психологии личности. Оказалось (по программе Слейда и Кжелдсена), что наибольшая не­сбалансированность (неопределенность) присуща элемен­ту «Келли». Если допустить, что разработанная этими авторами мера конфликтности валидна, можно утвер­ждать, что представления психологов о Келли далеко не однозначны (см. табл. 10).

Другая мера конфликтности (или амбивалентности) была предложена Франселлой и Криспом (74). Исполь­зуя программу INGRID Слейтера, они показали, что мера «расстояния» между одноименными парами кон­структов и элементов варьирует в зависимости от типа их вербального обозначения. Например, «идеальное Я» как конструкт и как элемент очень близки друг к другу. Но расстояние между конструктом и одноименным элементом «Я в моем нормальном весе» весьма велико у больных анорексией¹. Франселла и Крисп предположи­ли, что существует связь между расстоянием и амбива­лентностью. Пациентка ранжирует элементы по конструкту «Я в моем нормальном весе» несколько отлично от того, как она ранжирует этот элемент по другим конструктам. Правомочность такой гипотезы исследовалась Франселлой и Криспом в рамках более широкого исследования (75).

Итак, на сегодняшний день относительно различных мер конфликтности и амбивалентности можно сказать только то, что эти исследования весьма интересны и, как нам кажется, перспективны, однако пока еще слишком умозрительны.

Комментарий

Существует опасность, что показатели, использу­емые исследователями при обработке решеток, будут все более усложняться и становиться все более и более абстрактными. Как при этом избежать статистической неразберихи? Пожалуй, лучше всего будет провести небольшое исследование, задать себе такой вопрос:

¹ Анорексия — патологическое состояние, возникающее в подро­стковом возрасте и проявляющееся в сознательном, упорном ограни­чении приема пищи вплоть до отказа от еды с целью похудания.— Прим. ред.

121

если вы предлагаете какую-то меру для решетки, то способны ли вы проследить связь между предлагаемым показателем и теми операциями, которые выполняет испытуемый при работе с решеткой? Другими словами, если вы собираетесь дать вашему показателю название вроде «мера конфликтности креативности идеального Я», можете ли вы аргументированно объяснить, какие именно ответы испытуемого или какой тип статистиче­ской обработки позволяет дать вашему показателю именно это название? Можете ли вы обосновать выбор своего названия?

Впрочем, по мере роста популярности решеток, конечно, будут появляться все новые меры, показатели и баллы. Поэтому важно, чтобы психологи подводили хорошую теоретическую базу под то, что они собира­ются измерять на операциональном уровне. Лучше всего, на наш взгляд, если такой базой станет для них теория, которая дала начало методу репертуарных решеток.

Глава 5

МЕТОДЫ КОМПЬЮТЕРНОЙ ОБРАБОТКИ И СРАВНЕНИЯ РЕШЕТОК

Никогда еще машина не могла абстрагировать или обобщать. Эти процессы не подчиняются рациональным канонам и не сводятся к преобразованию символов, несмотря на то что в ряде случаев эти процедуры весьма полезны. ЭВМ способна, например, ликвидировать из­быточность данных в матрице. Сжатие матрицы в этом случае иногда ошибочно принимается за абстрагирова­ние, так как, казалось бы, большая совокупность данных сводится к сравнительно небольшому числу символов. Однако ЭВМ не обобщает, а всего лишь экономит символы, хотя, конечно, следует признать, что немногословность способствует более ясному мыш­лению. Тем не менее ликвидация языкового хаоса не означает абстрагирования, а экономия не порождает теоретического мышления. Бритва Оккама' — хирургический инструмент, а не творческий метод.

Дж. Келли (105, 290)

Компьютерная обработка

Статистические игры с решетками привлекают вни­мание многих несостоявшихся математиков, работа­ющих ныне в психологии. Программы становятся все сложнее: зачастую невозможно обнаружить никакой связи между машинной распечаткой результатов и действиями испытуемого при заполнении решетки. Мы не призываем к примитивизму и упрощению обработки, а лишь хотим предостеречь исследователей, склонных входить в азарт игры с числами: им следует помнить, что множество интересных сведений можно почерпнуть при непосредственном изучении «сырого» материала решеток (см. главу 4).

Сам Келли лелеял мысль о разработке и применении сложных статистических процедур для анализа реше­ток. В первом томе «Психологии личных конструктов» он в общих чертах наметил непараметрический метод факторного анализа. Первая программа компьютерной

¹ «Бритвой Оккама» называют один из принципов научного объяснения, выдвинутый средневековым английским философом-схоластом У. Оккамом. Согласно этому принципу, «сущности не следует умножать без нужды».— Прим. ред.

123

обработки была написана Фейджером (58) и позднее доработана Келли (107). Следующий значительный шаг был сделан Слейтером, описавшим в 1964 году свой метод «главных компонент»' для анализа ранговых решеток, причем как решеток со сходными элементами и конструктами, так и с различными элементами или конструктами. Представив психологическое простран­ство в виде гиперсферы, он нашел возможность числен­ного выражения взаимодействия между элементами и конструктами ранговой и оценочной решеток. В течение ряда лет недоступность его программ, находившихся под финансовым контролем Совета по медицинским исследованиям, лишала психологов возможности дви­гаться вперед. Были, конечно, и исключения. Банни-стер разработал программу раздельной кластеризации конструктов и элементов. Другие исследователи исполь­зовали модификацию кластерного анализа Мак-Квитти (139). Равенетт (167) разработал метод «двустороннего» анализа, проводимого без помощи ЭВМ и позволяюще­го «вычитать» влияние специфических элементов внут­ри каждого кластера конструктов.

Уилсон (222) поставила следующую проблему: «Иде­альный способ исследования связей между конструкта­ми и элементами требует одновременной стандартиза­ции строк и столбцов. Поэтому, хотя программа Слей-тера и представляет собой попытку обнаружения свя­зей между конструктами и элементами, она искажает эти связи, так как нормализуются лишь конструкты, а не элементы. Для выявления подлинных связей необхо­димо стандартизировать как столбцы, так и строки, однако, по утверждению Кеттела (45), метод получения единственного решения при одновременной стандарти­зации строк и столбцов еще не разработан. Это очень интересная статистическая проблема, имеющая боль­шое значение и для анализа решеток».

На сегодняшний день есть лишь несколько методов компьютерной обработки импликативных решеток. К ним относится модификация метода факторного анали­за Келли. При использовании этого метода исследова­тель сталкивается с извечной проблемой сравнения данных типа «пропуск — галочка»: и галочкам, и пропу-

¹ Метод главных компонент — один из наиболее распространен­ных методов факторного анализа. Не требует никаких априорных предположений о структуре данных. Позволяет получить однознач­ное решение. Выделяемые факторы (главные компоненты) ортогональ­ны (не коррелируют друг с другом) и упорядочены по величине, так что первая главная компонента объясняет максимальное количество дисперсии данных и т. д.— Прим. ред.

124

скам приписывается одинаковое значение, что вновь приводит к вопросу о неравномерности распределения элементов по полюсам конструктов.

Для преодоления этих трудностей была разработана программа подсчета биноминальной вероятности совпа­дения и несовпадения галочек в парах строк и столбцов биполярной импликативной решетки (66). Однако, как стало ясно сейчас, и это далеко не лучший способ обработки. В настоящее время разрабатывается совер­шенно новый подход к анализу данных импликативных решеток, базирующийся на модели субъективной веро­ятности. С помощью этой модели строится матрица сходства конструктов, подвергающаяся затем кластер­ному анализу по одному из существующих алгоритмов.

Для тех, кто интересуется статистикой и хотел бы расширить свои познания в области компьютерной обработки решеток, мы включили в эту главу общее обсуждение этой проблемы, в значительной степени заимствованное из работы Уилсон (222), где она подчерк кивает, что существуют две большие группы методов анализа ранговых и оценочных решеток.

Метрический факторный анализ¹

Главное преимущество методов этого типа заключа­ется в их доступности: в Великобритании и США они включены в коммерческие статистические пакеты прог­рамм (например, СПСН, или Статистический пакет программ для социальных наук, 154). СПСН включает в себя пять различных методов факторного анализа.

Анализ методом главных компонент (МГК). Он не накладывает ограничений на анализируемые данные (чего нельзя сказать про другие четыре метода). По существу, это анализ общей дисперсии данных, позво­ляющий обрабатывать столбцы и строки раздельно. Получаемые главные компоненты можно вращать при помощи алгоритмов, основанных на одном из трех критериев (варимакс, эквимакс и облимакс)². В итоге обработки строится факторное пространство.

¹ Более подробные и специальные сведения о различных алгорит­
мах факторного анализа читатель может найти, например, в книге
Харман Г. Современный факторный анализ.— М.: Статистика, 1972.—■
Прим. ред.

² Различные типы «вращения» факторов. Методы «вращения»
разработаны для получения более простой и интерпретируемой
факторной модели. В основе каждого метода лежит некоторый
критерий, который оптимизируется в процессе поиска решения.
Например, метод варимакс-вращения построен на критерии максими­
зации дисперсии факторных нагрузок на каждый фактор. В результа-

125

Остальные методы базируются на общей факторной модели, предполагающей, что каждая из факторизу-емых переменных имеет как общую, так и специфиче­скую компоненту, а интерес представляет только общая дисперсия.

Анализ методом главных факторов (МГФ) — наиболее широко используемый метод. Уилсон указы­вает, что он представляет собой разновидность более общего факторного анализа, рекомендуемого Руммелом (176), ему не присущи те допущения, которые лежат в основе общего факторного анализа, и он обладает дополнительным преимуществом: позволяет проверить лежащее в основе традиционной факторной модели предположение о том, что значение имеет только общая часть дисперсии конструктов. Одним из резуль­татов обработки является матрица ковариаций, обрат­ная матрице факторного отображения. Внедиагональ-ные элементы этой матрицы имеют значения, близкие к нулю, что увеличивает доверие исследователя к валид-ности окончательного решения, так как подтверждает, что в большую часть общей дисперсии вносят вклад все конструкты. Уилсон считает необходимым отметить, что решения, получаемые при помощи факторного анализа, как правило, обладают размерностью N/2. Это означает, что факторов примерно в два раза меньше, чем переменных. Если оказывается, что факторов слишком много для экономичного описания данных, в конечном решении число факторов можно уменьшить, а затем подвергнуть их вращению.

В основе двух оставшихся методов лежат как предположения, имплицитно присущие общей фактор­ной модели, так и некоторые дополнительные допуще­ния.

В основе Рэо-анализа лежит предположение о том, что факторизуемые переменные (конструкты) охваты­вают всю совокупность переменных, а элементы пред­ставляют собой выборку из общей популяции элемен­тов.

При проведении же Альфа-анализа предполагается, что включенные элементы представляют собой целую популяцию, а переменные — выборку из совокупности переменных. В этом случае решение можно распростра-

те этого метода ищется решение, при котором каждая переменная имеет максимальную нагрузку по одному из варимакс-факторов и минимальные нагрузки по другим факторам. Этот метод позволяет также получить ортогональное решение (некоррелирующие между собой факторы). Другие методы, как, например, облимакс, позволяют получить косоугольное решение, то есть решение, состоящее из коррелирующих факторов.— Прим. ред.

126

нить на всю совокупность конструктов. Уилсон утвер­ждает, что выбор техники должен определяться целью исследования. Обсуждение описанных выше методов можно найти также в работах Ная и его коллег (154).

Уилсон делает еще два замечания относительно программ факторного анализа, включенных в СПСН. Во-первых, они позволяют проводить факторный ана­лиз как матрицы корреляций, так и матрицы ковари-аций. Обе матрицы строятся на основе «сырых» дан­ных, однако факторные решения, получаемые методом главных компонент и методом главных факторов, отли­чаются друг от друга. Этого нельзя сказать о Рэо- и Альфа-анализах, а также о модификации факторного анализа Харриса (82). Получаемые при помощи этих трех методов решения для матриц корреляций и ковари-аций пропорциональны и, следовательно, значимо кор­релируют между собой, что, по мнению Уилсон, снима­ет проблему, с которой сталкиваются исследователи при использовании как метода главных компонент, так и метода главных факторов,— какую матрицу выбрать для факторизации.

Второе замечание Уилсон касается отношения числа элементов к числу факторизуемых конструктов и свя­занной с этим проблемы репрезентативности конструк­тов. В целом можно сказать, что при факторизации матрицы корреляций надежность решения в некоторой степени зависит от стабильности коэффициентов корре­ляции. Стабильность возрастает по мере увеличения количества элементов, между которыми подсчитывает-ся корреляция. Поэтому Уилсон советует там, где это возможно, использовать число элементов, в три раза превышающее число конструктов. Кроме того, размер­ность конечного решения можно случайно или искус­ственно ограничить неправильным выбором конструк­тов, то есть нарушив требование репрезентативности конструктов. Если выявляются или задаются конструк­ты лишь двух типов, то можно с полным основанием ожидать двухфакторного решения.

В работе Уилсон рассматриваются решения, опти­мальные с точки зрения статистики, но не с точки зрения психологии. Баннистер и Мэир (21) при работе с ранговой решеткой, в которой в качестве элементов использовались люди, обнаружили, что при увеличении числа элементов от 10 до 15 значительно уменьшается структурированность материала решетки.

127

Неметрические методы

В эту группу входят методы многомерного шкалиро­вания (195)'. В то время как метрические методы предполагают наличие линейной зависимости между факторами и переменными, техники многомерного шка­лирования предполагают только сохранение монотонно­сти конечного решения и анализируемой матрицы. Так, например, в ранговой и оценочной решетках порядко­вые отношения между конструктами в их связи с конкретным элементом (то есть по какому конструкту элемент оценивается наиболее высоко, по какому — вторым и т. п.) сохраняются в конечном решении, однако на основе этого решения ничего нельзя сказать о том, насколько выше элемент был оценен по данному конструкту, чем по другому. Уилсон отмечает, что в тех областях, где измерение преимущественно прово­дится по шкалам порядка или даже шкалам наименова­ния, меньший акцент на линейные связи становится преимуществом многомерного анализа неметрического типа. Но у этого метода есть и недостатки. Наиболее существенный практический недостаток заключается в том, что существует слишком мало коммерческих пакетов программ, доступных пользователям. Хотя неметрические методы развиваются уже давно (47), они далеко не так распространены, как метрические методы.

Наиболее исчерпывающая классификация неметри­ческих моделей, программ машинной обработки и спо­собов организации данных приводится в работе Шепар­да (194). Уилсон, однако, считает, что список Шепарда далеко не полон, а количество разработок растет «с устрашающей скоростью».

В работе Уилсон рассматривается также имплика-тивная модель Хейза (84), имеющая прямое отношение к импликативным решеткам. В качестве первичных данных в ней используются условные вероятности. Модель позволяет получить матрицу расстояний, кото­рая затем анализируется неметрическими методами. Преимущество модели Хейза, по мнению Уилсон, со­стоит в том, что она дает возможность обрабатывать асимметричные условные вероятности и определять веса (или значимости) полюсов конструктов. В соответ­ствии с этой комбинированной характеристикой кон­структы, наиболее тесно связанные с измерениями

¹ Подробнее об этом см.: Шепард Р. Н. Многомерное шкалиро­вание и безразмерное представление различий.— Психологический журнал, 1980, т. 1, № 4, с. 72—83.— Прим. ред.

128

получаемого решения,— это центральные конструкты, обладающие наибольшим весом. Они имплицируют большое число других конструктов, в то время как их имплицируют очень немногие конструкты. Уилсон под­черкивает, что определение центральных конструктов очень близко к представлению Хинкла о суперординат-ности (88). Она считает, что мера расстояния Хейза вместе с техникой неметрического многомерного шкали­рования является, по-видимому, первым валидным средством для определения размерности импликатив-ных решеток.

Описание других программ компьютерной обработки и методов статистического анализа можно найти в работах Ландфилда (114), Франселлы (66), Уилкокса (220), Гертина (79).

Сравнение решеток

Сравнение решеток различных типов

Репертуарным решеткам посвящено довольно много исследований, так как цели их разработок весьма разнообразны. При этом, однако, лишь немногочислен­ные работы посвящены сравнению решеток различных типов. Круг вопросов здесь таков: нацелены ли они на исследование одних и тех же образований? Насколько согласуются между собой данные, получаемые с по­мощью решеток различных типов?

Поиску ответа, например, на последний вопрос посвящена одна из работ Франселлы (63). При сравне­нии ранговой и оценочной решеток одного и того же испытуемого обнаружилось существенное расхождение результатов в ориентации конструктов в пространствах двух главных компонент.

В более позднем исследовании (69) коэффициент корреляции между этими двумя методами оказался равным 0,76. Эксперименты как в первой, так и во второй работе проводились на одном испытуемом. Причем, поскольку один из конструктов обнаружил межтестовую корреляцию «—0,47», ясно, что остальные конструкты, несмотря на различие используемых мето­дов, должны действительно сильно коррелировать меж­ду собой.

В 1967 году Мэир и Бойд сравнили результаты, полученные с помощью ранговой решетки и метода разбиения пополам (145). Надо сказать, что и до этого существовали доказательства сходства данных, получа­емых при помощи этих методов. Так, обследуя больных

5-492

129

с нарушениями мышления, Баннистер показал согласо­ванность результатов метода разбиения пополам (12) и обычной ранговой решетки (20).

Мэир и Бойд проводили свое исследование на 24 молодых правонарушителях, которые заполняли ре­шетки двух типов, одну сразу вслед за другой. Проце­дура повторялась, через две недели. В качестве элемен­тов использовались фотографии: 20 штук в методе разбиения пополам и 10 — в ранговой решетке. В каждом случае проводилось сопоставление конструктов похож на меня, похож на отца, похож: на мать с остальными 15 конструктами, а также сравнение связей между конструктами разных решеток. Ниже приводят­ся средние коэффициенты корреляции для трех кон­структов (по обоим типам решеток): 0,5 для конструкта похож: на меня (диапазон от —0,76 до 0,82); 0,57 для конструкта похож: на отца (диапазон от —0,64 до 0,91); 0,48 для конструкта похож: на мать (диапазон от —0,36 до 0,84). Эти средние значения значимы по крайней мере на уровне р<0,05 (для N=19). Означает ли такой широкий диапазон значений корреляций, что конструкт похож: на меня имеет для некоторых испытуемых противоположный смысл при работе с ранговой решет­кой и при методе разбиения пополам? Если это так, то в чем субъективная разница этих двух методов? Если можно было бы показать, что у испытуемых с отрица­тельным коэффициентом корреляции для конструкта похож на меня (—0,76) отрицательны и коэффициенты корреляции по другим конструктам, а у испытуемых с высоким коэффициентом корреляции по одному кон­структу высоки коэффициенты корреляций и по другим конструктам, то это приблизило бы нас к пониманию воспринимаемых испытуемым различий. Было бы еще лучше, если бы у этих испытуемых оказались высоки­ми коэффициенты корреляции и в тест-ритесте для обоих типов решеток. В результате проведенного иссле­дования Мэир и Бойд пришли к выводу, что применя­емые методы не взаимозаменяемы.

Хонесс (93) сравнил ранговую решетку с биполярной импликативной решеткой. В качестве испытуемых в эксперименте участвовали дети (средний возраст— 12,8 года), которым предлагались конструкты, получен­ные при анализе некоторых из составленных ими рассказов. В качестве элементов снова использовались фотографии. Первая группа детей сначала заполняла ранговую решетку, а затем, через неделю,— импликативную, через 4 недели — вновь ранговую. Вто­рая группа детей заполняла решетки в следующей

130

последовательности: импликативная, ранговая, импли-кативная. Корреляция между двумя методами внутри групп оказалась равной 0,50. Этот результат очень похож на результат, полученный Мэиром и Бойдом, однако статистически гораздо более значим (N=41).

Хонесс приводит и другие данные. Например, для импликативной решетки корреляция тест-ритест ока­залась значительно больше, чем для ранговой (0,82 и 0,66). Если исключить наименее стабильный конструкт, то эта корреляция достигнет соответственно 0,89 и 0,75. Импликативная решетка позволяет, по-видимому, полу­чить конструкты с более выраженной биполярностью: критерий биполярности Хонесса для конструктов ранго­вой решетки оказался равным 28,8%, а для конструктов импликативной решетки — 56,9%.

Келсолл и Стронгмен (108) сравнили импликативную решетку с решеткой, в которой использовались данные типа «пропуск — галочка». Оказалось, что паттерн кон­структов в целом очень сходен (р<0,001), однако и в этом случае наблюдается значительный индивидуаль­ный разброс.

Таким образом, различные типы решеток нельзя считать идентичными: различаются и восприятие зада­ния, и результаты. Ответить на вопрос, почему при помощи решеток разных типов мы получаем различные результаты, можно только путем тщательного исследо­вания задания, предлагаемого испытуемому. В этом случае мы, несомненно, узнаем что-то новое и о природе психологического измерения в целом.

Сравнение решеток одного типа

Если нас интересует паттерн связей между кон­структами, то оценить степень стабильности идентич­ных решеток, заполненных различными испытуемыми или одним и тем же испытуемым в различное время,— задача несложная.

Изучая нарушения мышления при шизофрении, Бан-нистер разработал статистический метод определения степени стабильности связей между конструктами в идентичных решетках. Если при первом исследовании второй конструкт связан высокой положительной кор­реляцией с конструктами 3, 4 и 5, то останутся ли эти связи такими же и при повторном исследовании? В табл. 19 показано, каким образом можно сравнить результаты двух исследований.

Сначала надо проранжировать коэффициенты корре­ляции между всеми парами конструктов, начиная с