Методическая разработка

1   2   3   4   5   6

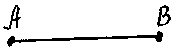
2. Определение. Два отрезка называются равными, если они имеют одинаковую длину.

3. Определение. Длину отрезка называют расстоянием между двумя точками.

4. Определение. Лучом (открытым лучом или полупрямой) называетсячасть прямой, на которые разбивается эта прямая любой ее точкой»

А - начало луча,

АО - луч,

n – луч

Если точка A отнесена к одной из полупрямых, то полупрямая называется замкнутым лучом.

Определение. Фигура, образованная двумя полупрямыми, исходящими из одной точки, называется углом.

Стороны - полупрямые, образующие угол.

Вершина - точка, из которой они выходят.

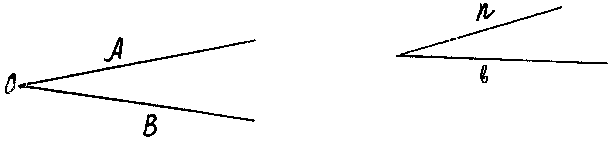
AOB, O, (n,b)

Определение. Два угла равны, если они имеют одинаковую угловую меру в градусах.

Определение. Треугольником называется фигура, которая состоит из трех точек, не лежащих, на одной прямой, и из трех отрезков, попарно соединяющих эти точки.



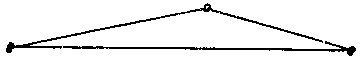
Определение. Треугольники называются равными, если у них соответствующие стороны равны и соответствующие утлы равны.

III. Аксиомы.

Аксиомы принадлежности точек и прямых (I группа)

I.1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Al

Bl

I.2. (аксиома прямой). Через любые две точки можно провести прямую, и только одну.


Аксиомы взаимного расположения точек на прямой и на плоскости (II группа)

II.1. Из трех точек на прямой одна и только одна лежит между двумя другими.
A─B─C

II.2. Прямая разбивает плоскость на две полуплоскости.



Аксиомы измерения отрезков и углов (III группа)

III.1. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

AB = AC + CB

III.1. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусам. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.



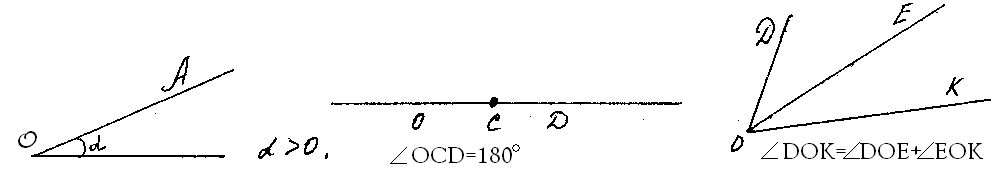
Аксиомы откладывания отрезков и углов (IV группа)

IV.1. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и только один.

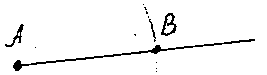AB = 3 ед.дл.

IV.2. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 градусам, и только один.

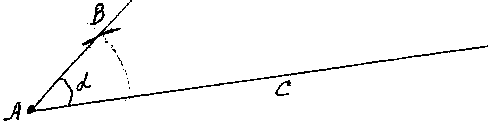0°<α<180°

IV.3. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной прямой

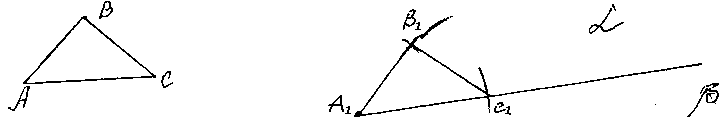∆ABC = ∆A1B1C1

Аксиома V группы (V постулат Евклида)

V.1. Через данную точку проходит не более одной прямой, параллельной данной прямой.

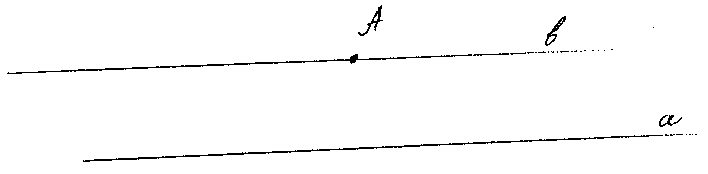a||b

Условие Заключение
Теорема. Если ... , то ...
Дано Доказать

Т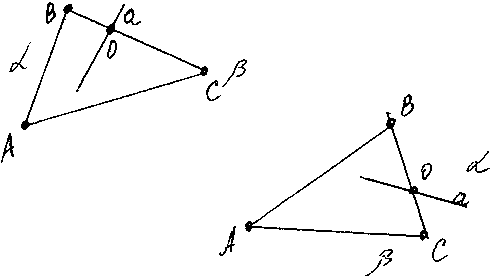еорема 1. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.

Дано: ∆ABC. Aa, Ba, Ca,
a∩BC=O

Доказать, что a∩AC=E
или a∩AB=K

Доказательство:

1. Пусть а разбивает плоскость на α и β, по аксиоме о взаимном расположении точек на плоскости.
Bα, Cβ, т.к. по условию a∩BC=O

2. Если Aα, то a∩AC=E, т.к. Cβ

3. Если Aβ, то a∩AB=K, т.к. Bα

Вывод. Прямая a пересекает сторону АС или сторону BC

Вопросы:

Доказать, что две различные прямые либо не пересекаются, либо пересекаются в одной точке.

Дана прямая и точки A, B, C, не лежащие на этой прямой. Известно, что отрезок АВ пересекает прямую, а АС – нет. Пересекает ли прямую ВС?

Может ли прямая, пересекающая одну из параллельных прямых, не пересекать другую?

Геометрия 7 класс.
Контрольная работа.

I вариант.

1. Вычислить смежные углы, если разность между ними 30°.

2. Даны два угла с общей вершиной. Стороны одного угла перпендикулярны к сторонам другого. Найти эти углы, если разность между ними равна прямому углу.

3. Сколько точек пересечения могут иметь 5 прямых, расположенных на плоскости (сделать рисунок).

II вариант.

1. Сумма данного угла и двух смежных с ним равна 330°. Чему равен данный угол.

2. Два тупых угла одной и той же градусной меры имеют общую сторону, а две другие их стороны взаимно перпендикулярны. Определить тупой угол.

3. Сколько прямых можно провести через 5 точек, расположенных на плоскости (сделать рисунок).