Geum.ru

Методическая разработка

Вид материалаМетодическая разработка

Содержание


Предисловие к пятому уроку.
Подобный материал:
1   2   3   4   5   6
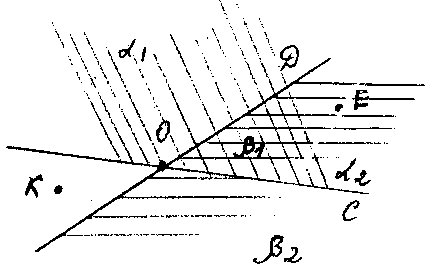пражнение 1. Начертите лучи OD и OС

Вопросы. Назовите полуплоскость с границей OD, содержащую луч ОС.
Назовите полуплоскость с границей ОС, содержащую луч ОД.
Что понимаем под внутренней областью угла ДОС?
Какие точки принадлежат внутренней области угла ДОС?
Какие точки принадлежат внешней области угла ДОС?

Вывод. Угол - два луча, исходящие из одной точки. Все углы (исключая развернутый угол) делят плоскость на две области - внутреннюю и внешнюю.

Упражнение 2. На экран спроецирован рисунок:



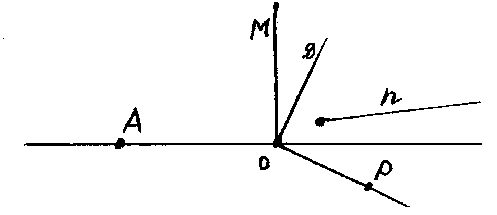
Вопросы. Какие из лучей являются внутренними лучами угла МОР? (Какие из лучей угла МОР проходят между его сторонами?)
Назовите углы, для которых луч OD является внутренним.
Назовите все внутренние лучи угла DOP.

Упражнение 3. Начертите произвольные углы ЛОВ, СМИ, ДЕР. Измерьте углы при помощи транспортира.

Напомнить учащимся об острых, тупых, прямых углах, а также о развернутом угле. Ознакомить с различными способами обозначения углов (угол может быть записан: 1, А, ВАС, (ab)). Вывод: Каждый угол имеет определенную градусную меру, большую нуля. Градусная мера развернутого угла 180°.

Упражнение 4. Начертите произвольный угол СДЕ. Изобразите внутренний луч АЕ.
Вопросы. Измерьте углы САЕ, ЕAD, САD - Как найти градусную меру угла САД, зная величины углов САЕ и ВД?

Вывод. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым внутренним лучом0

Упражнение 5. Начертите угол АОВ, развернутый. Угол DОВ – прямой.
Вопросы. Что можно сказать об углах АОD и DОВ?
Как называется луч ОD?

Вывод. Углы равны, если равны их градусные меры.

Упражнение 6. Расположение углов на плоскости.



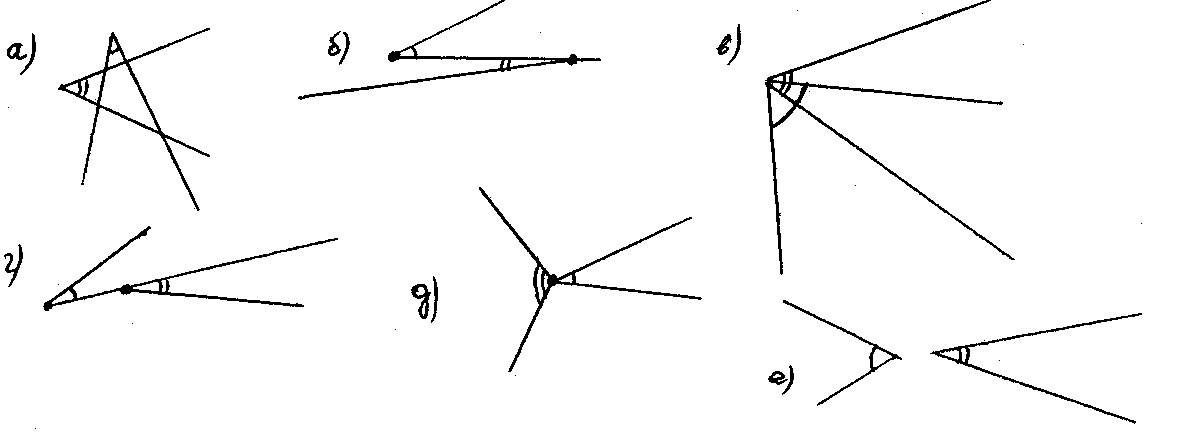
4. Построение.

а) Дано: ВАЕ

Построить: СDА такой, что CDА = BAE.

Построение.
  1. DC - луч.
    α1, α2 - полуплоскости,
  2. Окр. (D,r) - произвольный радиус,
    Окр. (А,r), получим точки М и К,
    М АВ, К АЕ
  3. Окр. (О,МЕ)
  4. Точка А пересечение окр. (D,r) и окр. (О, ME)
  5. DА - луч.
  6. Угол СДА – искомый.

Вывод. От луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньше 180°, и только один

б) Дано: АВС
ВД ― биссектриса.
Построить: ВД.
Построение:
  1. окр. (В,r), r - произвольный радиус,
    получим точки M и К, М ВС, К АС
  2. окр. (К,r)
  3. окр. (M,r)
  4. Окружности пересеклись в точке D
  5. BD - биссектриса угла АBС.

Итог урока.

Вопросы (на дом). 1. Построить угол, равный углу DОК.
2. Построить биссектрису угла DОК.
3. Можно ли утверждать, что любая точка отрезка, концы которого принадлежат внешней области угла ВОС, также принадлежат внешней области этого угла?
4. С помощью циркуля и линейки постройте угол 2°, если на плоскости дан угол, величина которого равна 13°.

ПРЕДИСЛОВИЕ К ПЯТОМУ УРОКУ.

В начале занятия учитель может сказать: "Героем сегодняшнего урока будет треугольник. Это фигура играет значительную роль в курсе геометрии. Обобщению свойств треугольника посвящен сегодняшний урок."

После подробной проверки домашнего задания учитель проводит беседу, в которой вводится понятие треугольника, его элементов, формулируется определение равенства двух треугольников, рассматриваются виды треугольников, выполняются задачи на построение треугольника равного данному. Причем соответственно равные элементы отмечаются на чертеже одинаковыми значками. При изучении этой темы учащиеся убеждаются, что использование букв и символов позволяет на математическом языке очень кратко записывать большие предложения, сформулированные на естественном языке.

Завершается урок практической работой. Домашнее задание содержит три задачи. Так как кроме этого учащиеся должны проработать материал урока. Учителю необходимо воспитывать отношение у учащихся к материалам урока как к источнику концентрированной научной информации.

Вводная беседа 5

Тема. Треугольник

План. 1. Проверка домашнего задания.
2. Треугольник.
3. Основные свойства треугольника
4. Вопросы.

Примерное содержание вводной беседы

1. Задание классу и учащимся у доски.

а) построить угол, равный данному,

б) построить биссектрису данного угла,

в) построить середину отрезка,,

2.

Упражнение I. Изобразите три точки, не лежащие на одной прямой. Соедините их последовательно отрезками.
Вопросы. Какую фигуру получили?
Сколько вершин?
Назовите их.
Сколько сторон?
Назовите их.
Назовите углы треугольника.

Задание. Продолжите сторону АС. При вершине С во внешней области образовался угол. ВСЕ - внешний угол треугольника.

Упражнение 2. Начертите треугольник СDЕ и при вершине Е построите внешний угол DЕК, К СЕ.
Вопрос. Чему равна сумма углов ДЕК и СЕД? Почему?

Упражнение 3. Начертите треугольник АВС и постройте середины его сторон АВ, ВС,
Отрезки ОD, DК, КО - средние линии треугольника АВС.
Отрезки ВК, СО, АД - медианы треугольника АВС.

Упражнение 4. Начертите три произвольных треугольника» Постройте в первом медиану, во втором - биссектрису, в третьем -высоту, выполняя соответствующие записи.



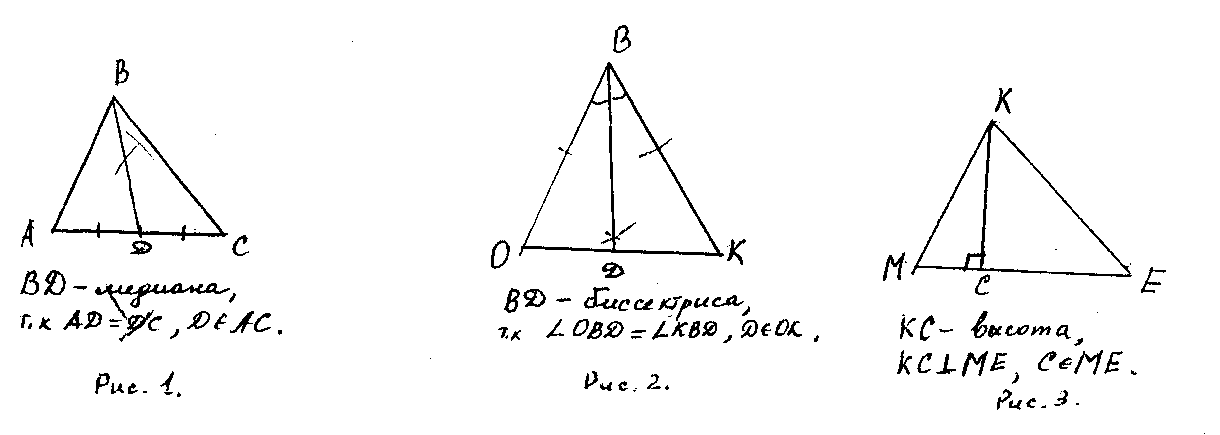
Учащиеся построения в треугольнике (рис. 3) выполняют вместе с объяснением учителя.

Упражнение 5. Начертите треугольники:
а) АВС, где А, B и С - острые углы.
б) МРК, где Р - тупой угол.
в) РDЕ, где D – прямой.