Geum.ru

Методическая разработка

Вид материалаМетодическая разработка

Содержание


Предисловие к шестому уроку.
Тема. Окружность.
Построение курса
Подобный материал:
1   2   3   4   5   6


Вопрос. Как называются построенные треугольники?

Упражнение 6. Дано: ∆АВС; Построить: ∆А1В1С1 такой, что А1В1=АВ, А1С1=АС А=А1.

Построение. 1. А1D – луч
2. На луче от начала в заданную полуплоскость откладываем А1, DA1E = BAC
3. Строим окр. (А1,АС), получим точку С1, С1А1D
4. окр. (А1,АВ), получим точку В1, В1А1Е
5. Строим отрезок В1С1
6. ∆А1В1С1 – искомый, т.к. А1В1 = АВ, А1С1 = АС, В1А1С1 = ВАС.

Вывод. От начала луча в заданную полуплоскость можно построить треугольник, равный данному.
∆АВС = ∆А1В1С1,: это значит, что А1=А, В1=В, С1=С и АВ = А1В1, АС = А1С1, ВС = В1С1.
Равенство треугольников понимаем как равенство трех пар углов и трех пар отрезков с концами в вершинах этих углов.

Упражнение 7.На рисунке изображены равные треугольники с некоторыми отмеченными одинаковыми значками соответственно равными элементами.



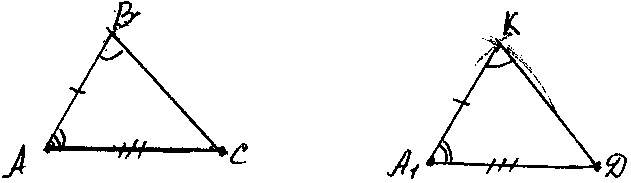
Запишите равенства.

Урок завершается практической работой.
  • начертите треугольник АВС,
  • постройте медиану BD, DАС,
  • постройте среднюю линию ВD, где МВС, DАС,
  • постройте биссектрису внешнего угла ВСК, где КАС
  • Найдите периметр треугольника ABC, сделав необходимые измерения.

Вопросы (на дом). 1. Постройте два треугольника, имеющих общую сторону, чтобы периметры треугольников были равны,
2. В тупоугольном треугольнике АВС (В - тупой) постройте высоту треугольника, исходящую из вершины А.
3. Разделите прямой угол при помощи циркуля и линейки на 4 равные части.

ПРЕДИСЛОВИЕ К ШЕСТОМУ УРОКУ.

После разбора упражнений из домашнего задания следует перейти к изучению темы урока. Окружность, центр, радиус, диаметр, хорда окружности - все эти понятия знакомы учащимся из курса математики 5-6 классов. Поэтому решение упражнений 1-3 способствует повторению и закреплению основных знаний по этой теме.

Пользуясь таблицами или предварительно заготовленными на доске чертежами, предлагается рассмотреть расположение окружности и треугольника на плоскости, взаимное расположение двух окружностей на плоскости без строгих обоснований, а только на наглядно-интуитивной основе.

Для закрепления предлагается провести диктант. Проверка происходит с помощью кодоскопа или другого проектирующего прибора.

После записи домашнего задания необходимо предупредить учащихся о том, что на следующем уроке тетради будут собраны на проверку.

Вводная беседа 6

Тема. Окружность.

План. 1. Проверка домашнего задания.
2 Окружность.
3. Расположение: прямой и окружности на плоскости, треугольника и окружности на плоскости, двух окружностей на плоскости.
4. Вопросы.

Примерное содержание вводной беседы

Упражнение I. Изобразите отрезок АВ
Начертите прямую a.
На прямой отметьте произвольную точку O.
На прямой a постройте отрезок, равный данному и имеющий один из концов в данной точке O.

Вопросы. Сколько таких отрезков можно построить?
Что можно сказать о длине этих отрезков?
Можно ли построить точки, которые от точки О были бы удалены на длину отрезка АВ?
Какую фигуру образуют эти точки?

Упражнение 2. Начертите окружность с центром А и радиусом R.
Отметьте произвольную точку В такую, что Вокр (АD)
А - центр окружности.
АВ - радиус.
СD - диаметр (СD = 2АВ), Сокр. (А,АВ), Dокр.(А,АВ).
ВЕ - хорда, Еокр. (А,АВ).

3. Расположение прямой и окружности на плоскости.



Р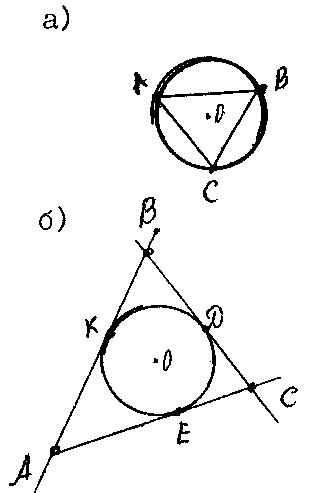асположение окружности и треугольника на плоскости.

Отметьте три произвольные точки А, В, С, лежащие на окружности.
Строям отрезки АС, АВ, ВС.
В этом случае окружность называют описанной около треугольника.

Начертите окружность с центром O и радиусом K, на ней три точки К, D, Е. Постройте касательные к окружности в каждой из точек К, D, Е. Отметьте точки пересечения касательных, Получили треугольник ABC. В этом случае говорят, что окружность вписана в треугольник.

Взаимное расположение двух окружностей на плоскости. а) окружности не имеют общих точек.



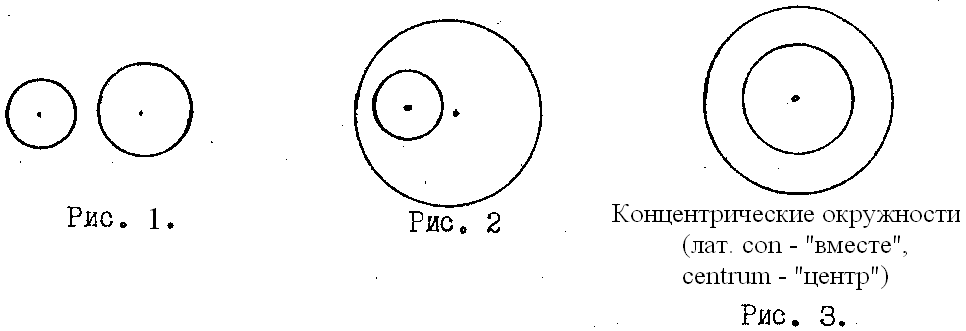
б) Окружности имеют одну общую точку (общую касательную).



в) Окружности имеют две общие точки.



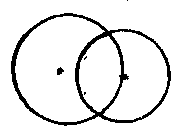
Вопрос. Могут ли две окружности иметь три общие точки?

Урок завершается диктантом.

Текст диктанта.

Начертите окружность с центром O и радиусом.
  1. Отметьте на окружности произвольную точку A, начертите отрезок ОА. Какова его длина?
  2. Каково расстояние от точки O до любой точки окружности?
  3. Отметьте на окружности произвольную точку B. Начертите отрезок АВ. Как он называется?
  4. Начертите отрезок СD, проходящий через точку O, концы которого лежат на окружности. Чему равна длина отрезка СD? Как называется отрезок СD?
  5. Начертите произвольный луч с началом в точке O. Обозначьте точку пересечения с окружностью. Может ли этот луч пересекать окружность еще в одной точке?
  6. Проведите через центр окружности произвольную прямую. Сколько точек пересечения имеет прямая с окружностью?
  7. Сколько можно провести хорд данной окружности?

Для успешной проверки и анализа проведенного диктанта полезно воспользоваться записями ответов, предварительно нанесенными на пленку кодоскопа или другого проектирующего' прибора.

Вопросы (на дом). Начертите окружность с центром O и радиусом R. Постройте хорду ДЕ и разделите ее пополам. Как расположена хорда DЕ и диаметр окружности, проходящий через середину DЕ?
2. Рассмотрите взаимное расположение окружности и угла на плоскости.
3. Начертите окружность с центром А и радиусом r. касающуюся данной окружности с центром O и радиусом R в точке Е внутренним образом. На окружности с центром А отметьте две произвольные точки. Постройте отрезок, соединяющий эти точки и точку Е. Получили треугольник. Каково расположение треугольника и окружности с центром O и радиусом R?

ЛЕКЦИЯ 1

Логическое построение курса планиметрии

Определение: Геометрия - наука, рассматривающая свойства фигур, "Фигура есть то, что содержится внутри какой-нибудь дли каких-нибудь границ" (по Евклиду).

Определение: Планиметрия - раздел геометрии, в котором рассматриваются свойства таких фигур, все части которых помещаются на одной плоскости»

ПОСТРОЕНИЕ КУРСА
  1. Основные понятия (неопределяемые).
  2. Определяемые понятия.
  3. Аксиомы (Аксиома - предложение, принимаемое без доказательства, рассматриваемое как исходное при построении той или иной математической теории (постулат по Евклиду)).
  4. Теоремы (Теорема - математическое предложение, истинность которого устанавливается или опровергается при помощи доказательства).
    Следствия. Так называют те предложения, которые составляют непосредственный вывод из аксиомы или теоремы,

I. Основные понятия (по Евклиду)

Точка, прямая.
"точка есть то, что не имеет частей".
"прямая линия есть та, которая одинаково расположена относительно всех своих точек".

II. Определяемые понятия

Определения. Так называют предложения, в которых разъясняется, какой смысл придают тому или другому названию.

1. Определение. Отрезком называется часть прямой, ограниченная с обеих сторон