Geum.ru

Денисенко Алена Дмитриевна, учитель математики Р. п. Благовещенка, 2004 Обоснование принципов отбора материала методическая разработка

Вид материалаМетодическая разработка

Содержание


Дано: АВС, А=90
Подобный материал:

Благовещенская муниципальная средняя

общеобразовательная школа № 2

Благовещенского района

Алтайского края


Методическая разработка урока геометрии в 8 классе

по теме:

«Теорема Пифагора»

Выполнила


Денисенко Алена Дмитриевна, учитель математики


Р.п. Благовещенка, 2004

Обоснование принципов отбора материала


Методическая разработка урока геометрии в 8 классе по теме «Теорема Пифагора» создана на основе учебника А.С. Атанасяна Геометрия. 8 класс. М.; Просвещение – 2002 г.

Тип урока – урок получения новых знаний.

Цель урока: организовать усвоение теоремы Пифагора и выработать умение применять данную теорему при решении задач. В соответствии с целью урока отобраны методы, приемы, содержание.

Наиболее эффективным методом на уроке явился метод информационно- коммуникационных технологий. Компьютер дает следующие инструменты:
  1. Интерактив, то есть взаимодействие ученика и учителя.
  2. Мультимедиа. Представление объектов и процессов не традиционным текстовым описанием, а с помощью фото, видео, графики, анимации, звука. На экран выводится портрет Пифагора, чертежи древних математиков.
  3. Коммуникативность. Возможность непосредственного общения, оперативность представления информации, контроль действий учащихся при решении предложенных задач. Учитель задает вопросы, дети имеют возможность тут же проверить правильность ответов с помощью слайдов.

Кроме того, на уроке используются следующие методы:
    • Эмоциональное слово учителя о древнегреческом математике Пифагоре. Используются иллюстрации для того, чтобы вызвать интерес.
    • Элементы занимательности (толкование шуточного изречения «Пифагоровы штаны во все стороны равны», формулировка теоремы в стихотворной форме, решение старинной задачи, нетрадиционное домашнее задание).
    • Индивидуальная работа.
    • Фронтальный опрос.

Информационно- коммуникационные технологии восполняют отсутствие наглядных и раздаточных материалов.

Логика построения урока соответствует логике усвоения темы.


Тема: «Теорема Пифагора».

Цели урока:

  1. Образовательная: организовать усвоение теоремы Пифагора и выработать умение применять данную теорему при решении задач.
  2. Развивающая: способствовать развитию математического мышления, формированию умения устанавливать причинно-следственные связи.
  3. Воспитательная: развивать сотрудничество учителя с учащимися, интерес к предмету, к истории математики.


Тип урока: Урок получения новых знаний.


Оборудование: компьютер, мультимедиа-проектор, карточки(приложение 1).


Ход урока.


Этапы урока
Деятельность учителя.
Деятельность ученика.

1.Организационный момент. Сообщение темы и целей урока.

(1 минута)
Входит в класс. Приветствует учеников.


Учитель сообщает тему урока и предлагает учащимся провести разминку, чтобы сформулировать задачи урока (разминка предусматривает повторение учащимися знаний, необходимых для изучения нового материала).
Приветствуют учителя стоя.

Садятся, после разрешения учителя.

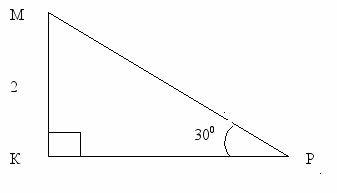
2.Актуализация знаний учащихся.

(3 минуты)


Формулировка проблемы.

(2 минуты)
Разминка.

1.Чему равна площадь квадрата?

2.Чему равна площадь прямоугольного треугольника?

3.Разложите на множители а2-в2

4.Расскройте скобки (а+в)2.

Слайд 1


- Какой треугольник изображен на рисунке?

- Как называются стороны прямоугольного треугольника?

- Назовите катеты и гипотенузу.

-Найдите катет МК, если известно, что угол Р=300, а гипотенуза МР=6см. (На карточках рис.1).

Слайд 2


- Найдите гипотенузу МР, если известно, что угол Р=300, а катет МК=2см.

Можете вы найти катет КР по данным рисунка?

Сегодня мы познакомимся с теоремой, с помощью которой научимся решать подобные задачи.

Сформулируйте задачи, стоящие перед вами на уроке.


Так кто же такой Пифагор, именем которого названа эта теорема.

Выходят к доске и записывают правильные ответы.


Рассматривают рисунки на карточках.

Устно отвечают на вопросы.


Затрудняются ответить.


Познакомиться с формулировкой теоремы, узнать, кто такой Пифагор, значение теоремы, научиться применять теорему

3. (слово учителя о Пифагоре)

(3 минуты)


Изучение нового материала.

(15 минут)
Слайд 3.

В Древней Греции жил ученый Пифагор (родился он около 580 г. до н.э., а умер в 500 г. до н.э.). О жизни этого ученого известно немного, зато с его именем связано ряд легенд. Рассказывают, что он много путешествовал, был в Индии, Египте, Вавилоне, изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. Так, на юге Италии, которая была тогда греческой колонией, возникла так называемая пифагорейская школа. Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. В школе существовал декрет, по которому авторство всех математических работ приписывалось Пифагору. Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд, что установить о Пифагоре правду не возможно.
  • Ребята, знаете ли вы что-нибудь связанное с именем Пифагора?



  • Обо всем этом мы и поговорим.

Слайд 4.

Запишем тему урока: «Теорема Пифагора».

Слайд 5.

В современных учебниках теорема сформулирована так:

«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

».

Давайте нарисуем прямоугольный треугольник и запишем эту формулировку в обозначениях.

АВС, С=900, АВ2=АС2+ВС2


с2=а2+в2


Слайд 6.

Запишите теорему Пифагора для треугольника КРО.

Слайд 7.

Во времена Пифагора Формулировка теоремы звучала так:

«Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника,

равновелик сумме квадратов, построенных на его катетах»

или

«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах»

Теорема Пифагора имеет богатую историю. Долгое время считали, что до Пифагора эта теорема была не известна. В настоящее время установлено, что эта теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора. Видимо, Пифагор узнал о ней во время одного из своих путешествий в Вавилон или Египет. За восемь веков до нашей эры эта теорема была хорошо известна индийцам под названием «правила веревки» и использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму.

На протяжении веков были даны многочисленные доказательства теоремы Пифагора, их существует более 150. Мы рассмотрим шесть доказательств.

Слайд 8.

Доказательство для равнобедренного треугольника.

Древнекитайское доказательство.



Древнеиндийское доказательство.


Доказательство Евклида.



Доказательство Аннариция.


Доказательство из учебника.

Слайд 9.

Доказательство для равнобедренного треугольника.

Простейшее доказательство теоремы получается в случае равнобедренного треугольника. Вероятно, с него и начиналась теорема. Квадрат, построенный на гипотенузе, содержит четыре треугольника, а на каждом катете построен квадрат, содержащий два треугольника. Из рисунка видно, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Смотрите, а вот и «пифагоровы штаны во все стороны равны».

Слайд 10.

Древнекитайское доказательство.

Данный рисунок использовали для доказательства теоремы Пифагора в Древнем Китае.

На рисунке воспроизведен чертеж из древнейшего китайского трактата .

Слайд 11.

Древнеиндийское доказательство.

Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Венец знания» крупнейшего индийского математика 12 века Бхаскары помещен чертеж с характерным для индийских доказательств словом «смотри!».

Слайд 12.

Доказательство Евклида.

В 1 книге «Начал» Евклид доказывает теорему Пифагора с помощью данного чертежа. На гипотенузе и катетах прямоугольного треугольника строятся соответствующие квадраты и использует здесь он равенство треугольников.

Слайд 13.

Доказательство Аннариция.

Багдадский математик и астроном 10 в. ан-Наризий (латинизированное имя Аннариций) доказывает теорему Пифагора по рисунку. Квадрат на гипотенузе разбит у Аннариция на 5 частей, из которых составляются квадраты на катетах. Метод равносоставленных фигур был очень популярен в древности.

Все древние доказательства теоремы Пифагора были геометрическими. Древние греки так боялись алгебры и фактически свели ее к геометрии. Более подробно мы рассмотрим одно из алгебраических доказательств, которое приведено в нашем учебнике.

Слайд 14.

Рассмотрим прямоугольный треугольник с катетами а, в, с. Докажем, что с2=а2+в2.

Используем приемы древних математиков.

Достроим треугольник до квадрата со стороной а+в. Площадь S этого квадрата равна (а+в)2. С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников и квадрата со стороной с. Площадь каждого треугольника равна ½ав, площадь квадрата равна с2. Поэтому S=4· ½ав+ с2. Таким образом, (а+в)2=4· ½ав+ с2. а2+2ав+в2= 2ав+ с2. Откуда получаем: а2+в2= с2.

Итак , мы рассмотрели несколько доказательств теоремы Пифагора. Теперь давайте посмотрим какие возможности дает нам теорема Пифагора.

Слайд15.

Какие элементы прямоугольного треугольника можно найти с её помощью.

Слушают и смотрят на экран.


Некоторые ученики могут сформулировать саму теорему или известную фразу: «Пифагоровы штаны во все стороны равны».


Записывают в тетрадях тему урока.


Рисуют прямоугольный треугольник и переводят формулировку теоремы на язык математических символов.

Записывают формулировку в обозначениях.

АВС, С=900, АВ2=АС2+ВС2


с2=а2+в2 .


КРО,  Р=900, КО2=КР2+РО2


Слушают и наблюдают за слайдами.


Ученик показывает указкой на слайде.


Сначала слушают и смотрят доказательство, а затем записывают доказательство в тетрадь.


Ответы ученики записывают на доске.

4. Закрепление изученного материала.

(10 минут)
Слайд 16.(рис.2)

Теперь давайте попробуем составить по рисунку, используя данную теорему, если это возможно, верное равенство.

Значит, х2=62+82 х=10.


Слайд17. (рис.3)

Можем мы использовать теорему в данном случае?

В данном случае теорему Пифагора использовать нельзя, так как не известно, о каком виде треугольника идет речь.

Итак, значит, для каких треугольников можно использовать теорему Пифагора?


Слайд 18.

Решим одну старинную задачу, в которой будет «работать» теорема Пифагора. Задача записана у вас на карточках.

Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.


Дано: АВС, А=900

АС=117 стоп, АВ=125 стоп.

Найти: СВ.

Слайд 19.

Решение задачи.

Пусть СВ=х стоп.

Тогда, используя теорему Пифагора,

получаем: 1252=1172+х2, х2= 1252-1172

,

х2= (125-117)(125+117) ,

х2=8·242

х= 4·2·2·121 ,

х= 2·2·11 ,

х= 44.

Что мы обозначили за х.


СВ= 44 (стопы).

Что нужно было найти?


Ответ: 44 стопы.

Слайд 20.

Решите теперь задачу, сформулированную в начале урока. Найдите катет КР по данным рисунка.

Записывают в тетрадях самостоятельно, затем один ученик записывает правильный ответ на доске.


Ученики делают вывод, что теорема Пифагора применяется только для прямоугольных треугольников.


Слушают и смотрят решение задачи, не записывая её в тетрадь.


Отвечают на проблемный вопрос, заданный в начале урока.

Решают в тетрадях самостоятельно, затем один ученик записывает правильный ответ на доске.

5. Подведение итогов урока.

(3 минуты)
Слайд 21.

Докажите, что мы сегодня выполнили задачи урока, сформулируйте теорему Пифагора.


А может быть, тем ребятам, кто не решился сейчас отвечать, поможет стихотворение.

Слайд 22.

Послушайте стихотворение: «Теорема Пифагора»

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путем

К результату мы придем.


Обогатил ли вас урок и чем?

Несколько учеников проговаривают формулировку теоремы Пифагора.


Читает наизусть

заранее подготовленный ученик.


Рефлексия.

Домашнее задание.

(3 минуты)
Слайд 23.

Домашнее задание.

П.54, вопрос 8;

Часто математики записывали свои задачи в стихотворной форме. Одна из задач индийского математика 12 века Бхаскары пойдет вам на дом.


«На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в том месте река

В четыре лишь фута была широка.

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?»

Слайд 24.

Давайте вместе построим рисунок.


-Какой геометрической фигурой можно изобразить тополь?

-Что случилось с тополем?


-Тополь сломался под корень?


Итак, получили рисунок. Дома оформите и решите задачу.

Урок окончен. До свидания.


Задача дана на карточках каждому ученику.

Один ученик читает вслух, остальные следят.


Работают в тетрадях.


Ответ: отрезок (изображают отрезок).

Ветра порыв его ствол надломал.

Осталось три фута всего от ствола.



Приложение 1


Классная работа.

Т
еорема Пифагора.



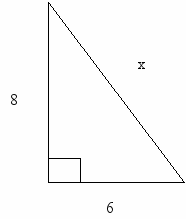
Рис.2


Рис.1





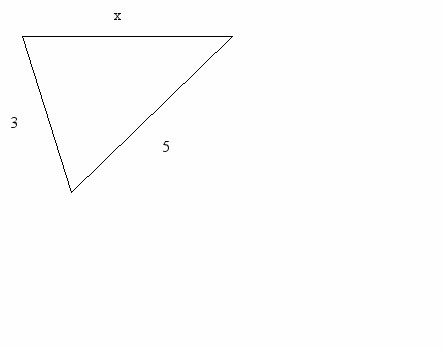
Рис.3





Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.



Домашнее задание.

П.54, вопрос 8;


«На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в том месте река

В четыре лишь фута была широка.

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?»